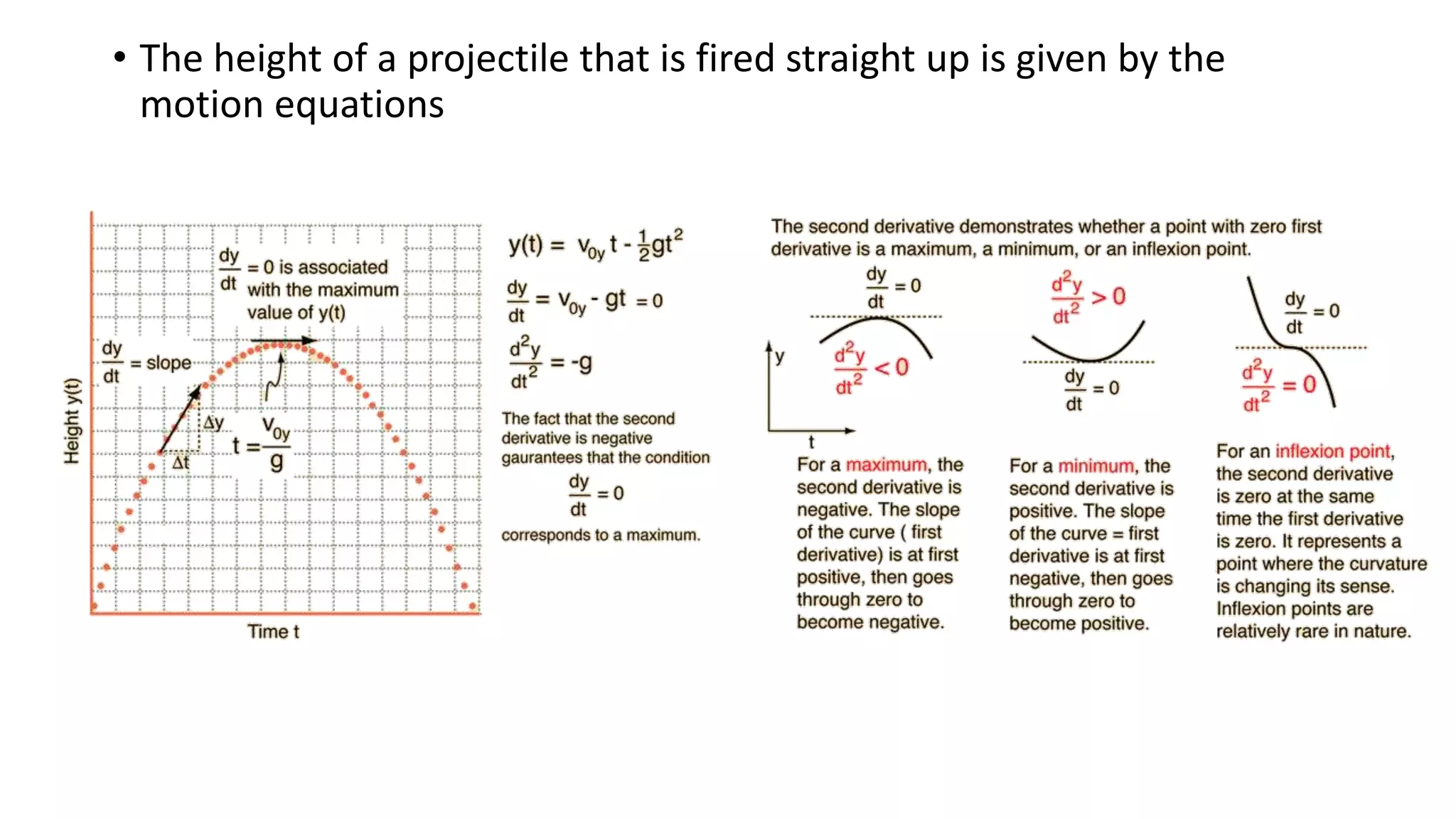
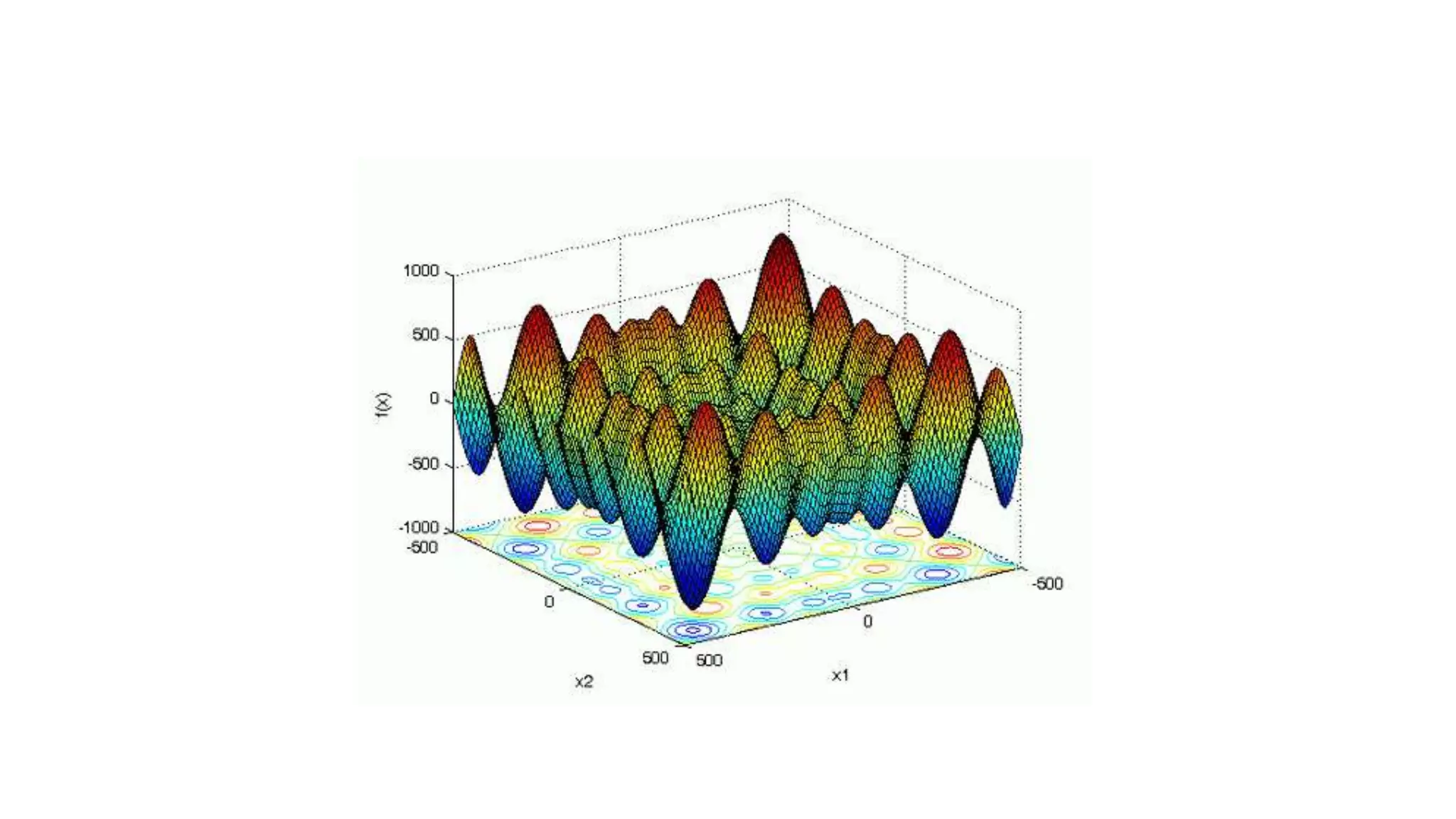
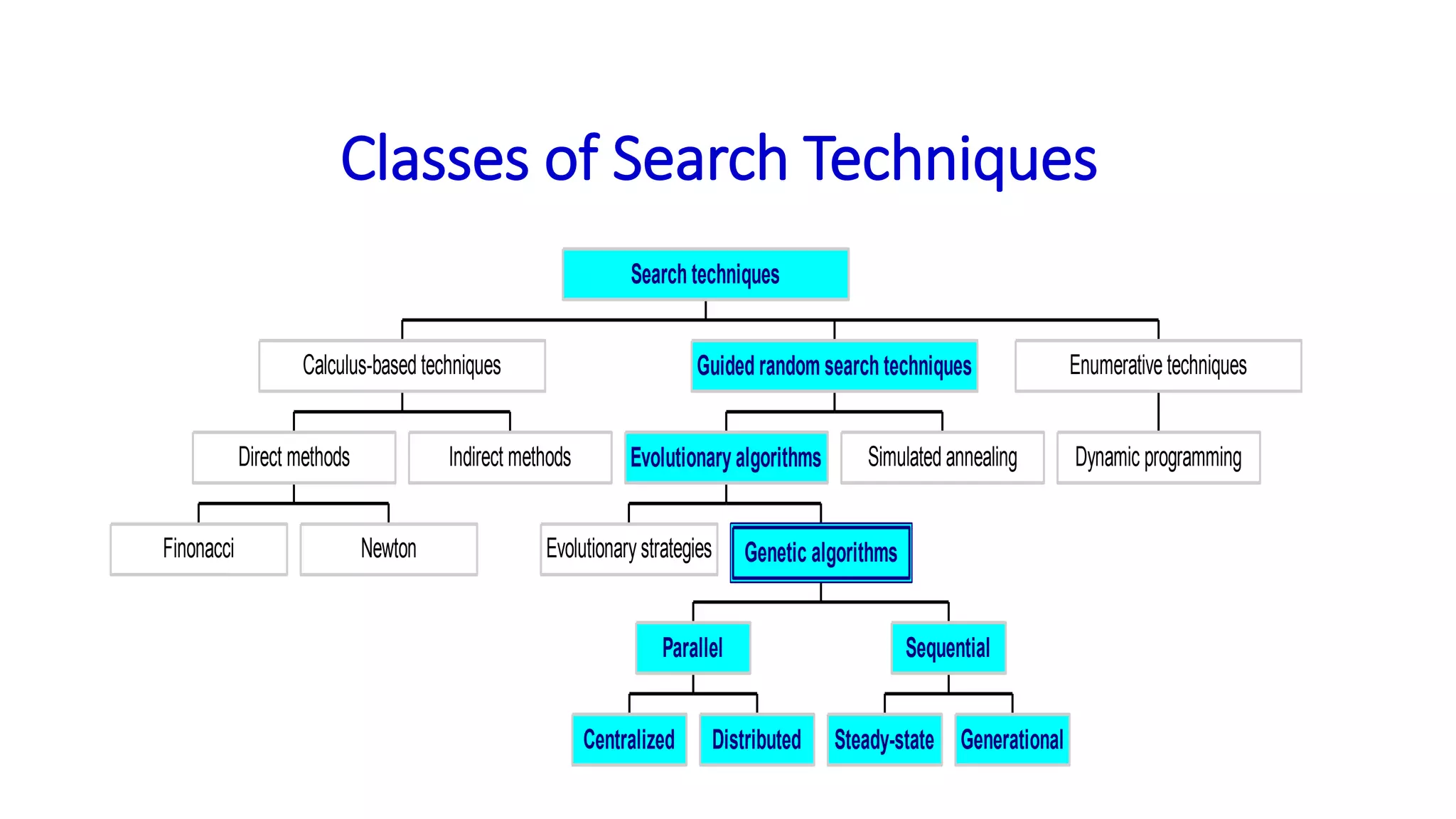
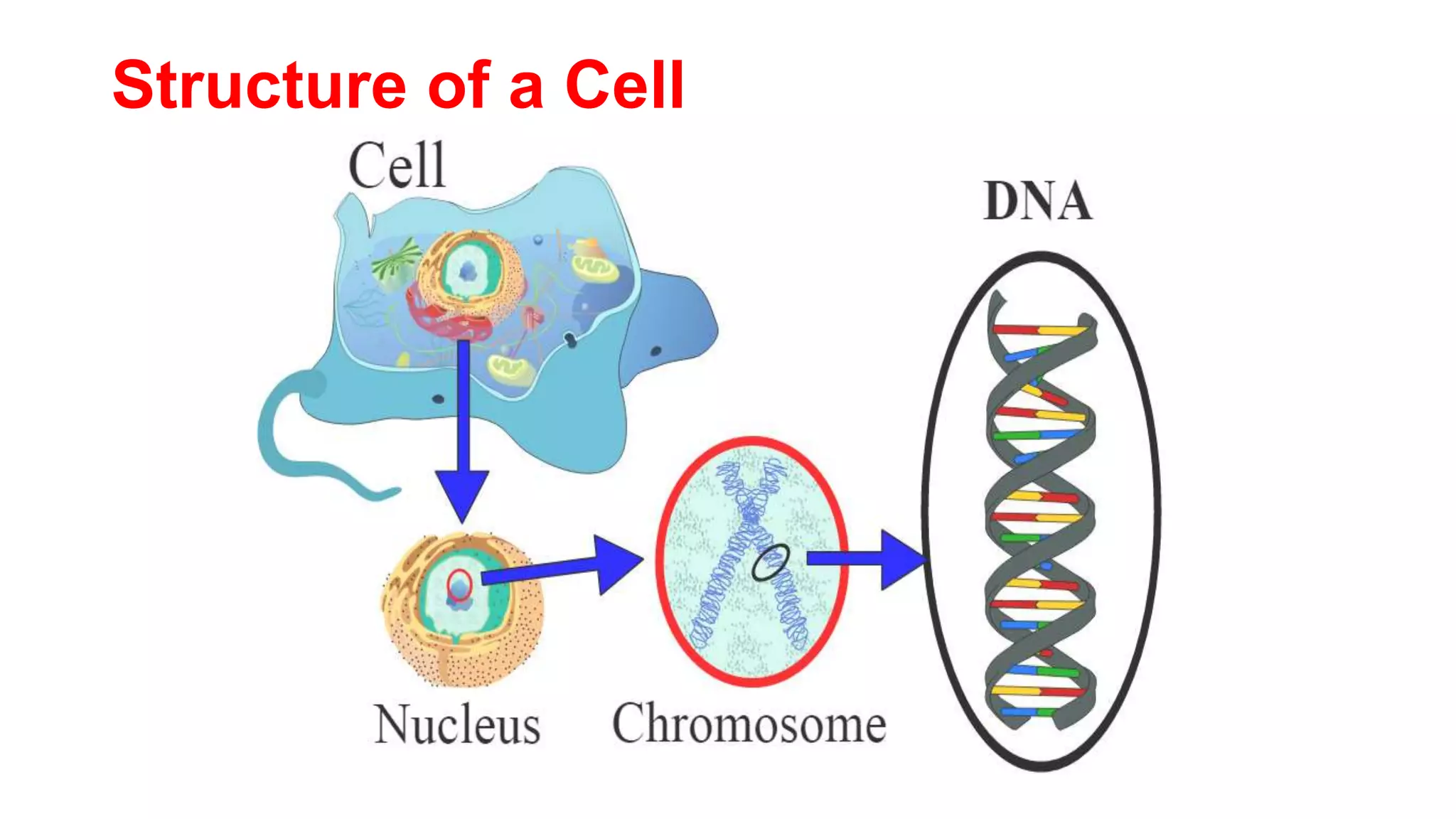
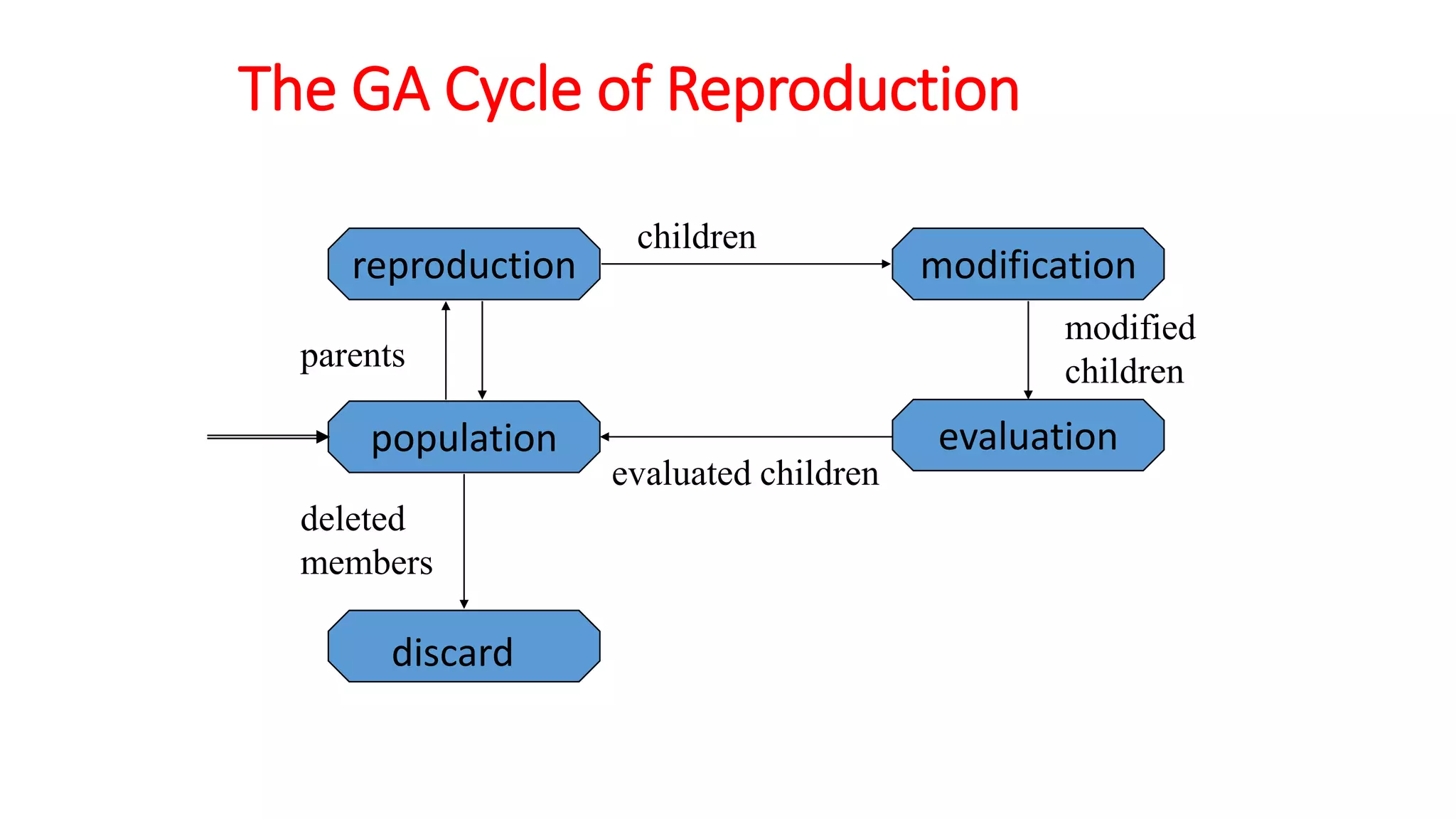
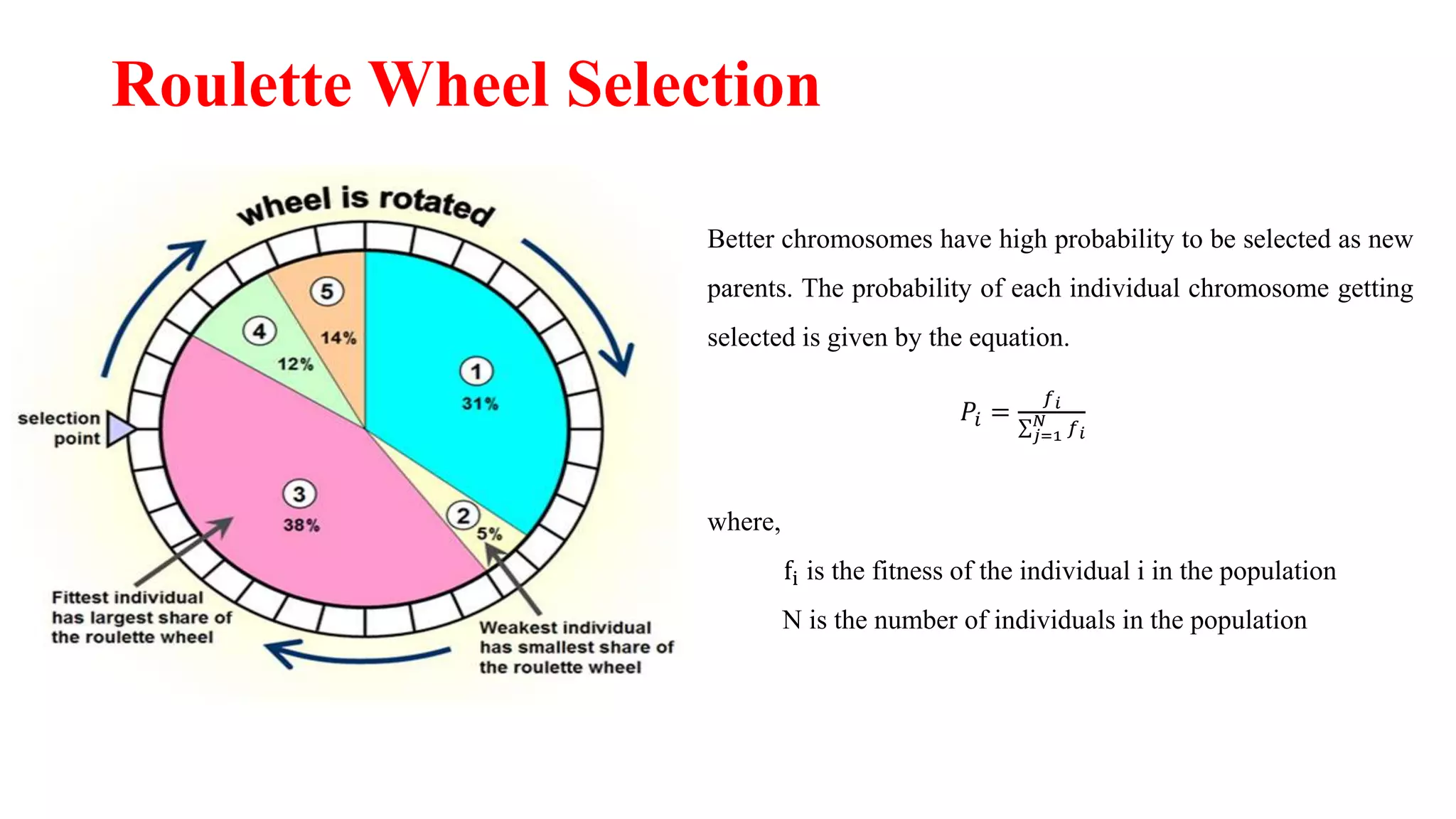
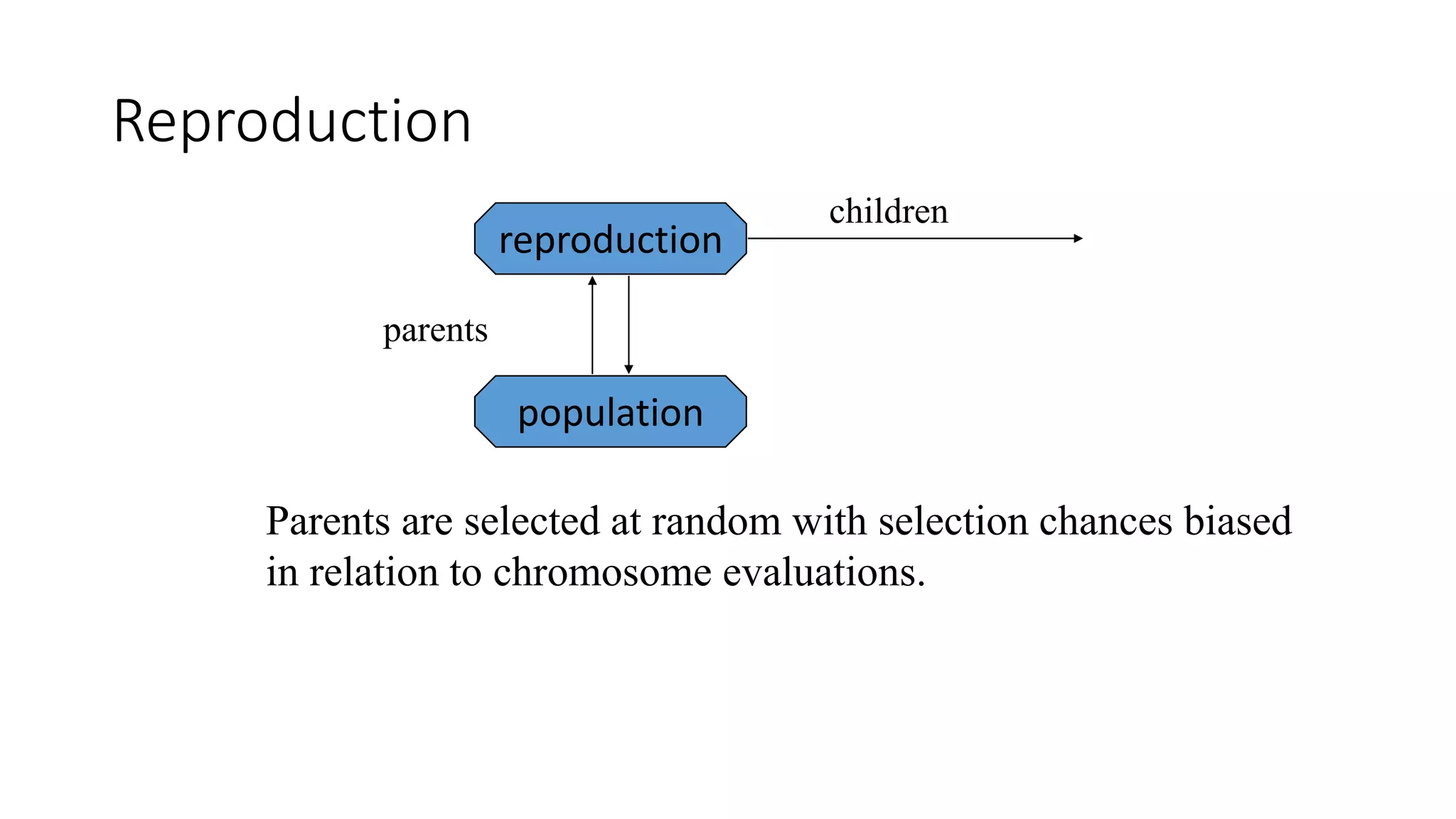
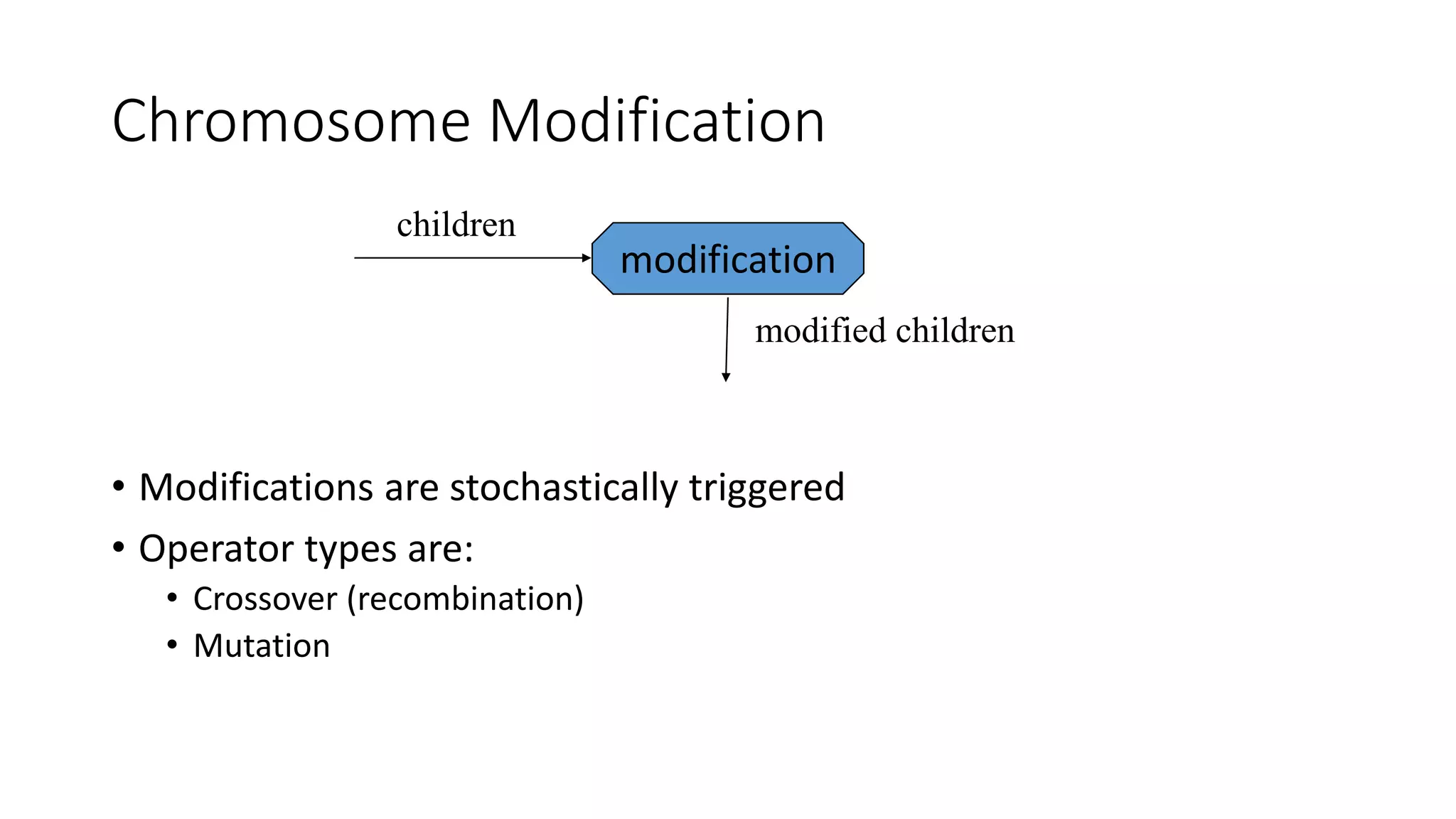
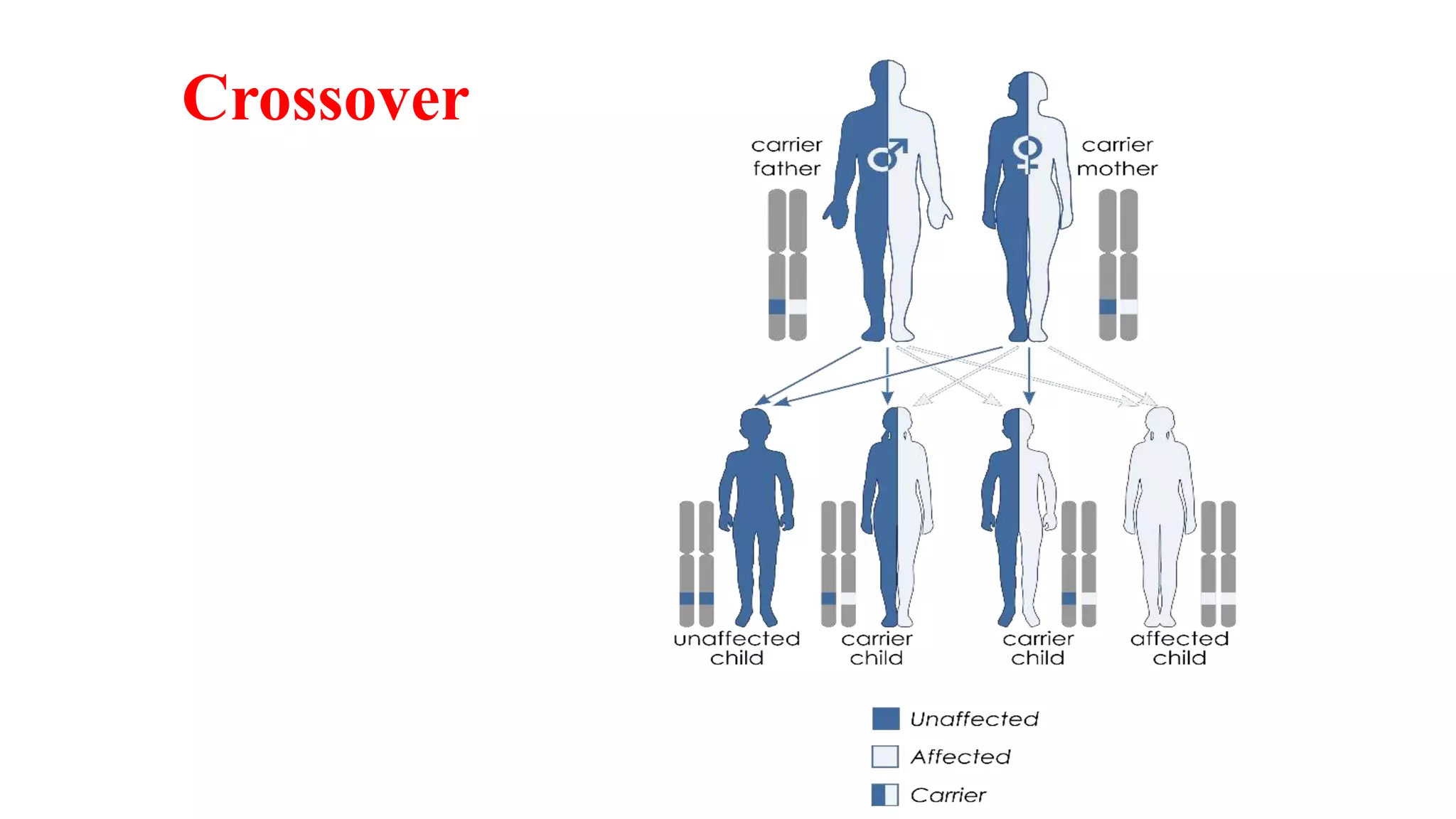
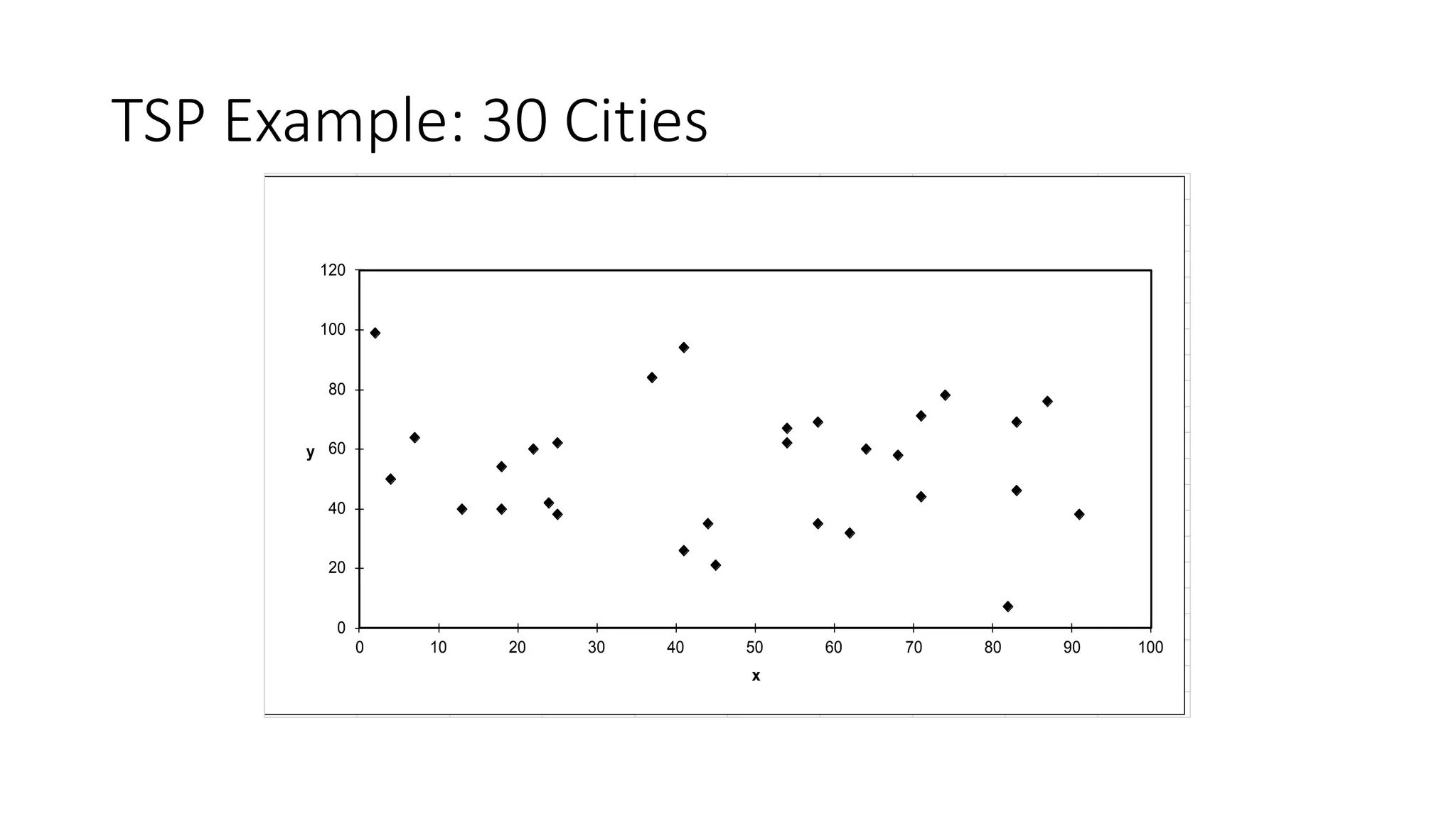
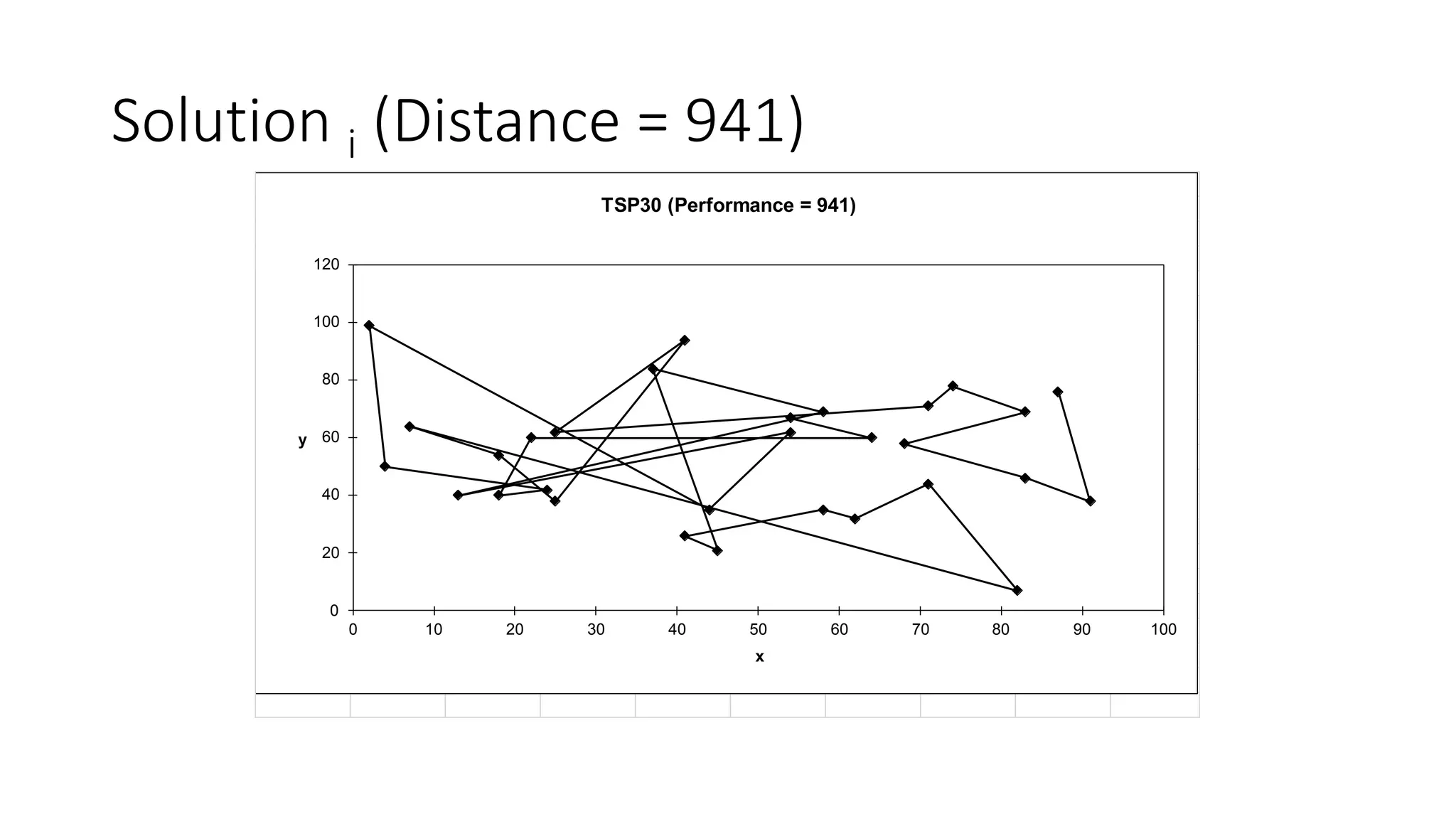
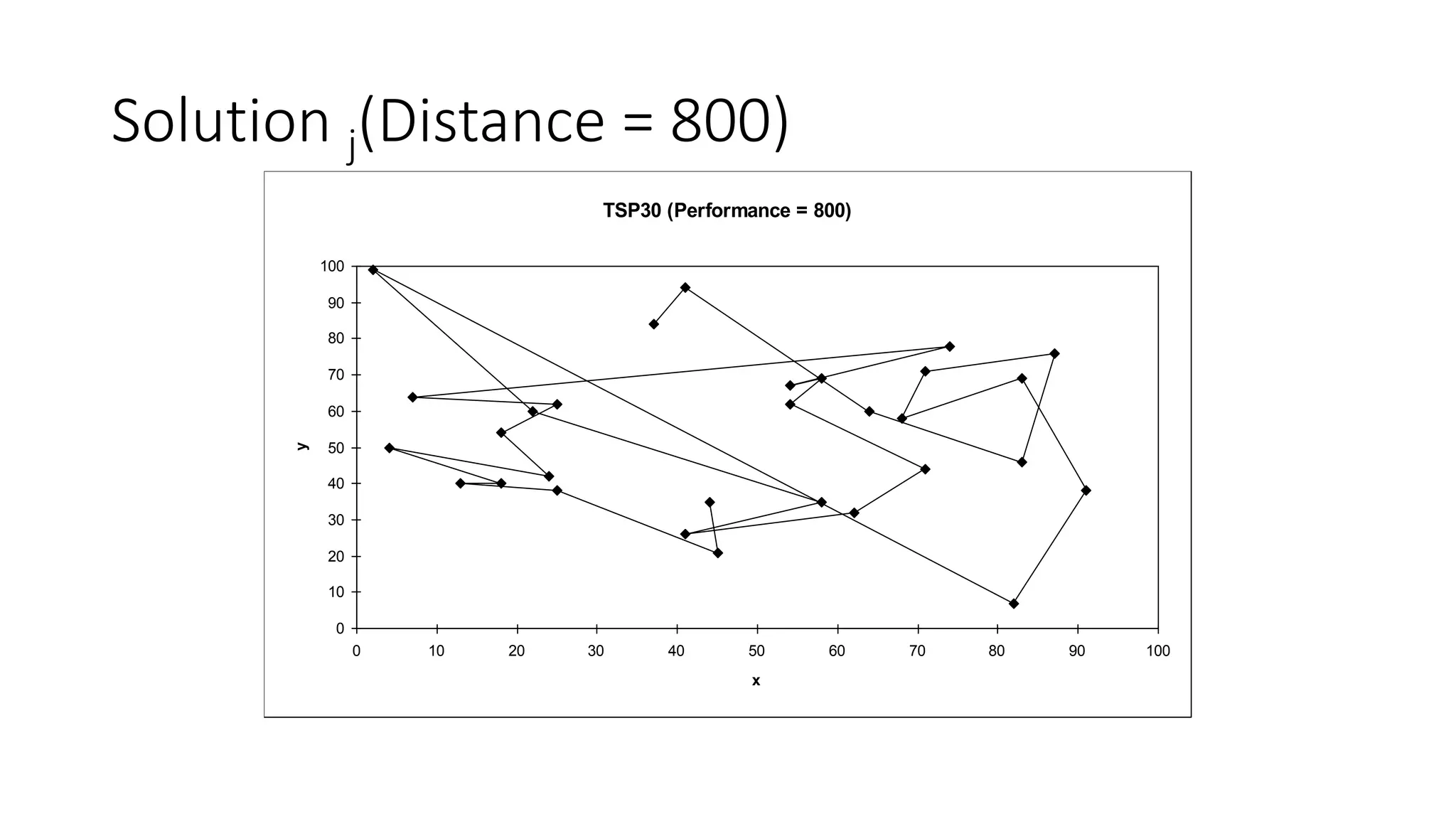
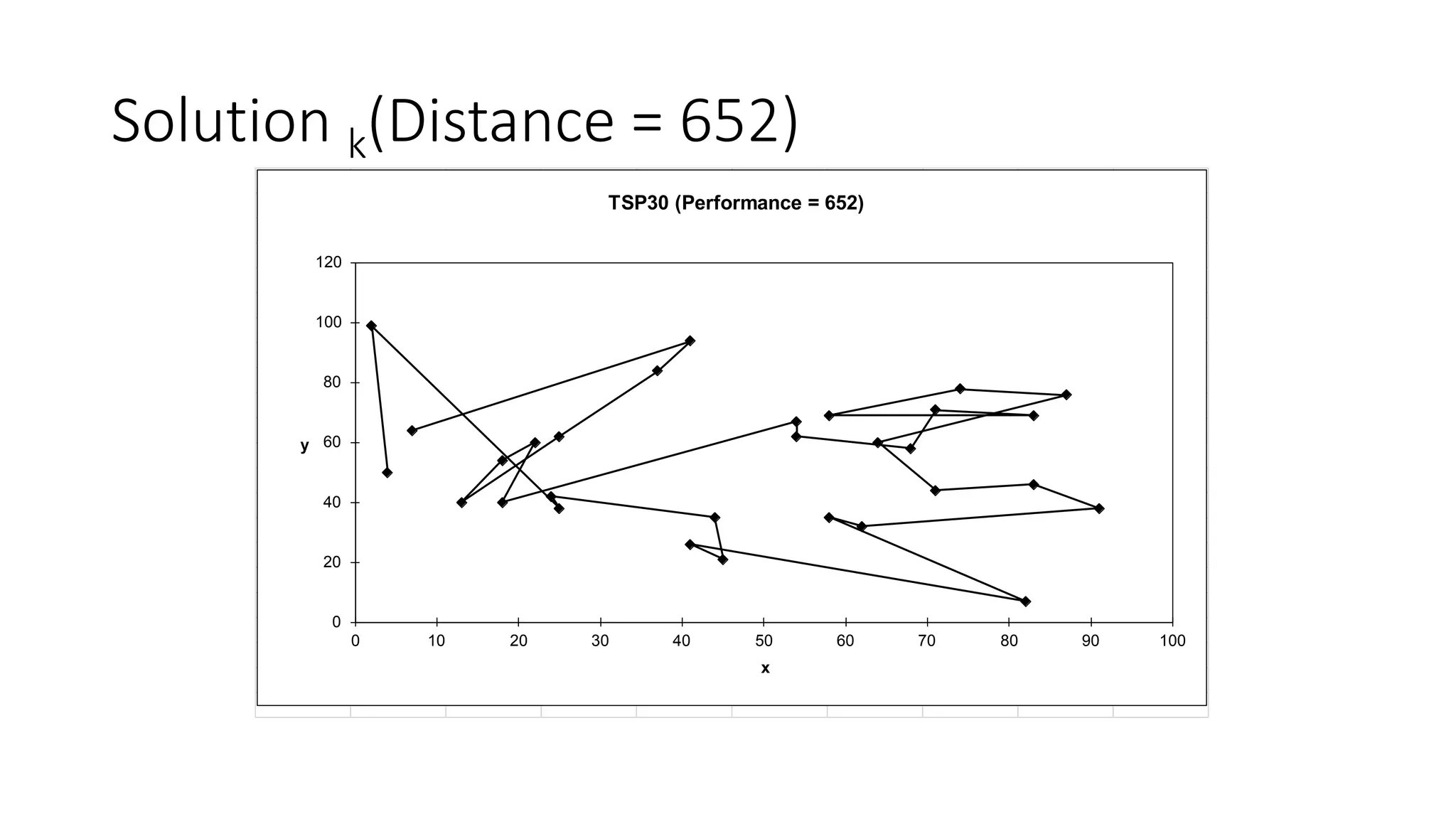
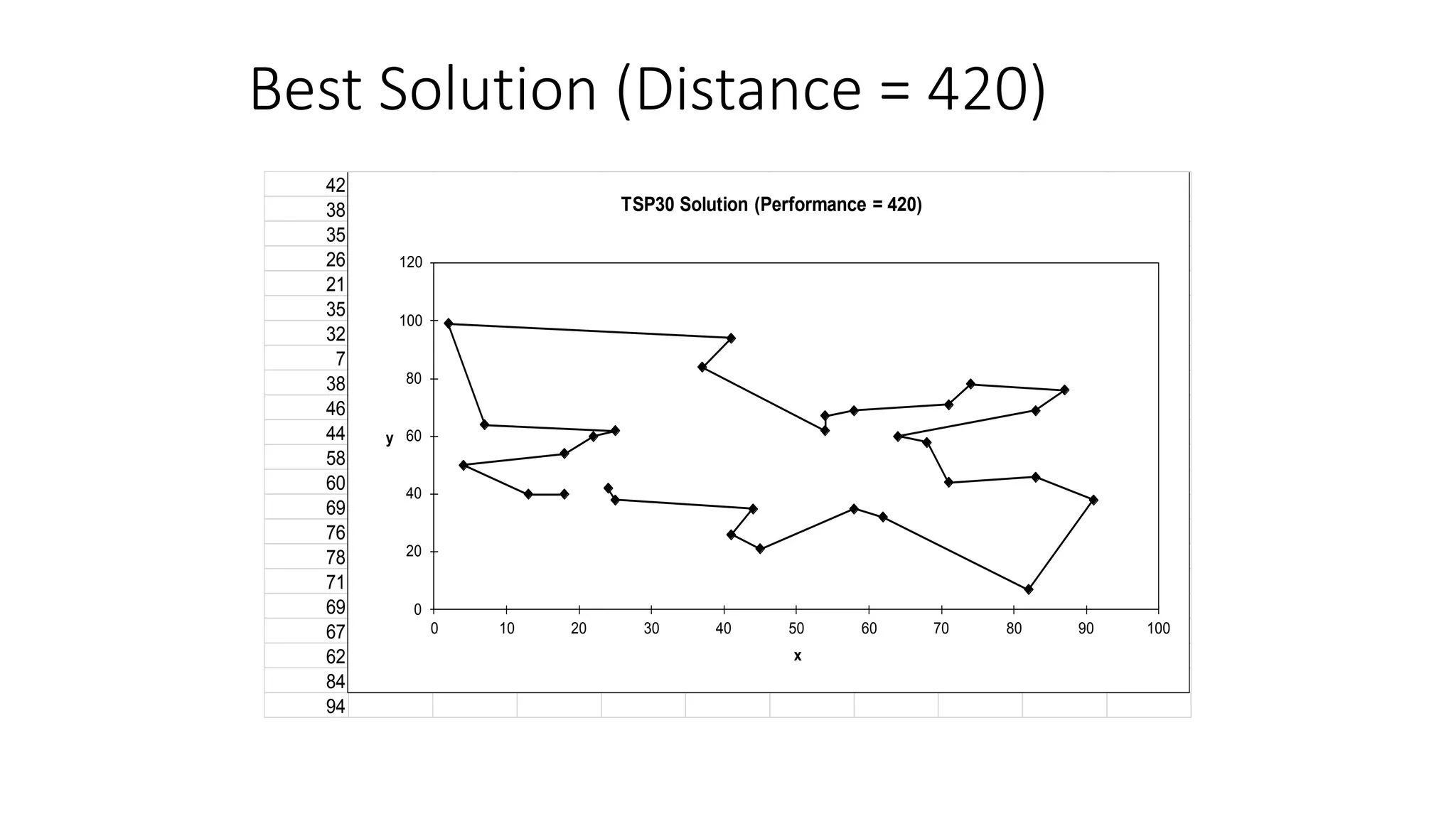
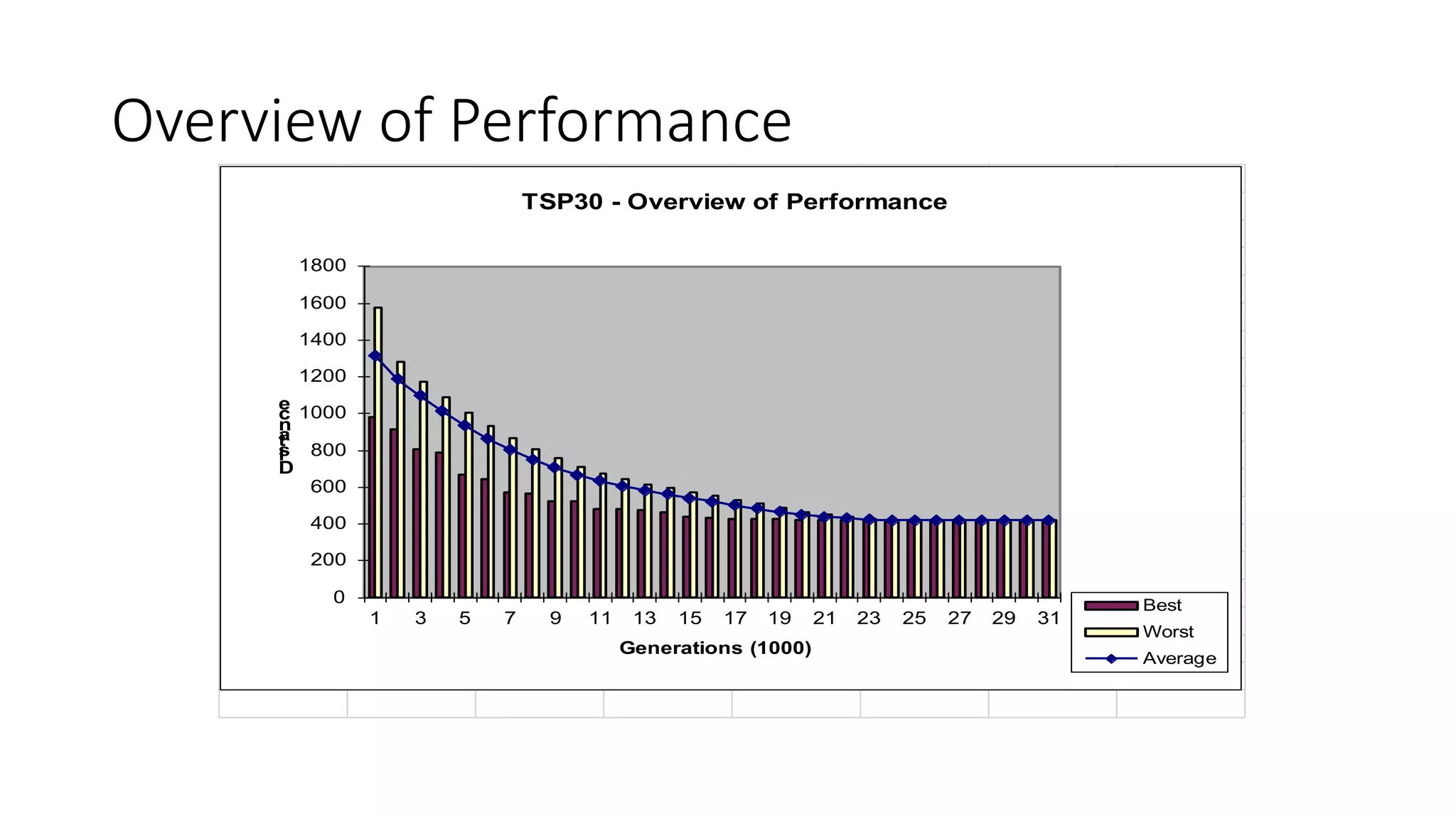
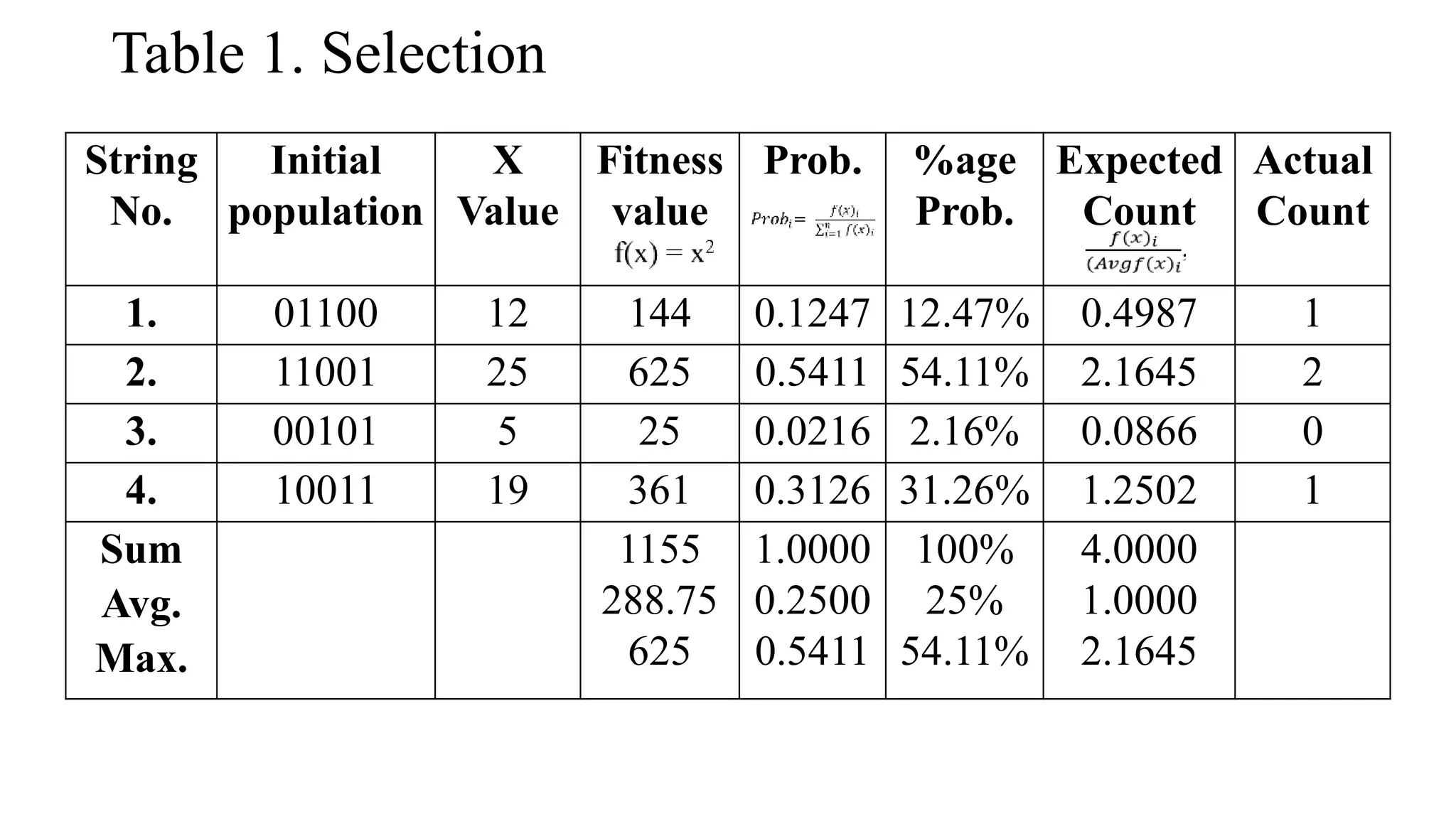
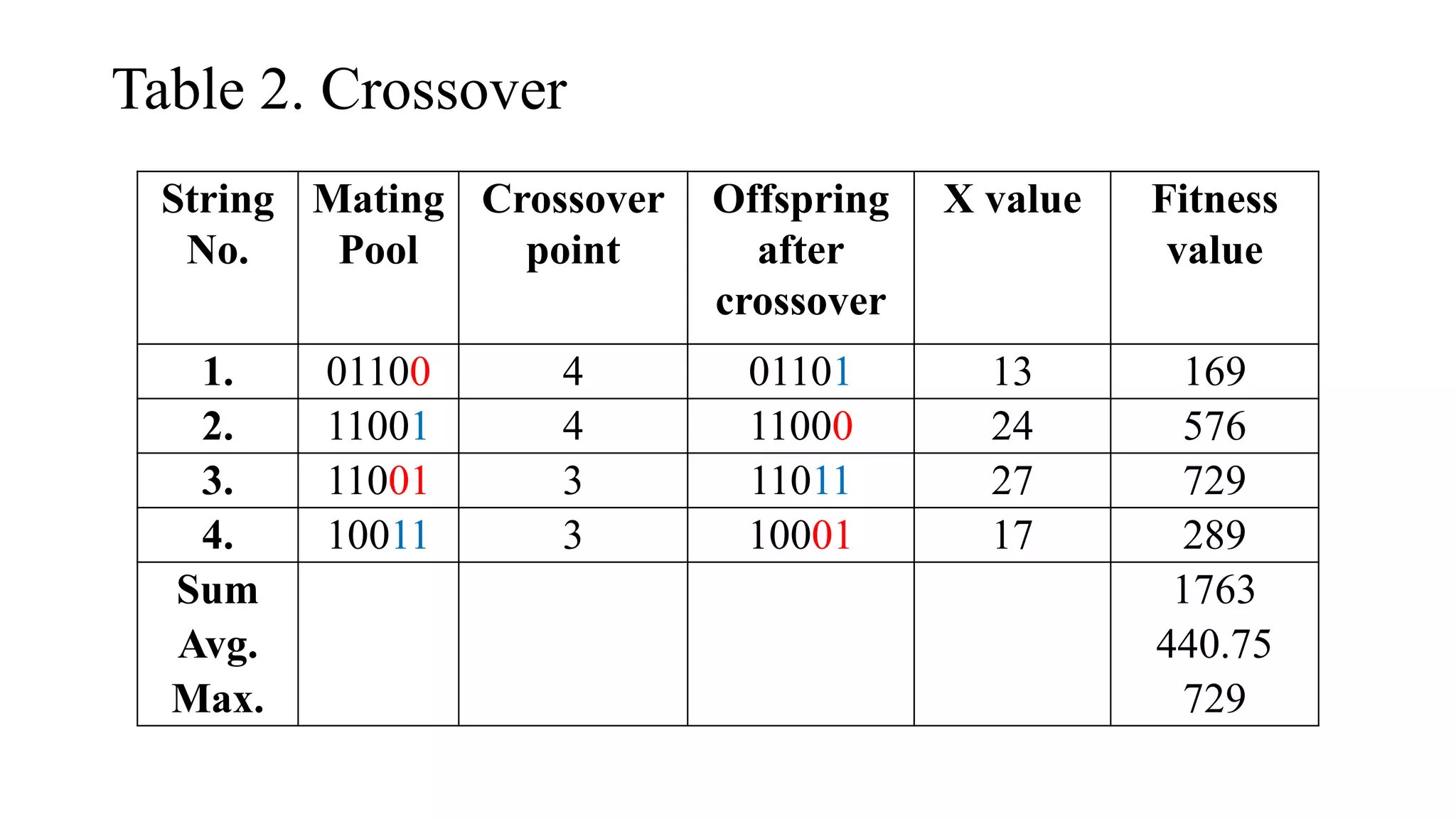
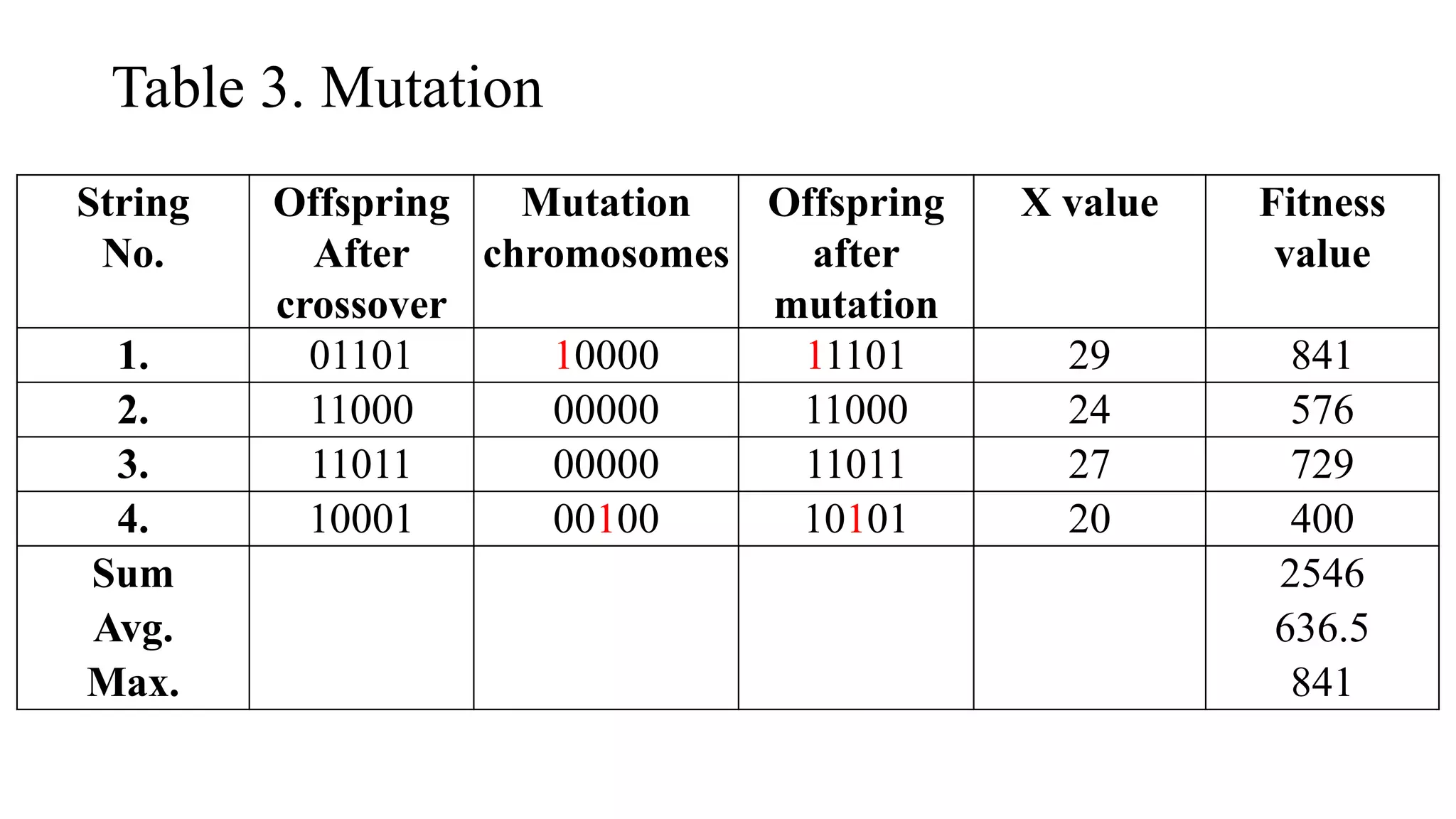
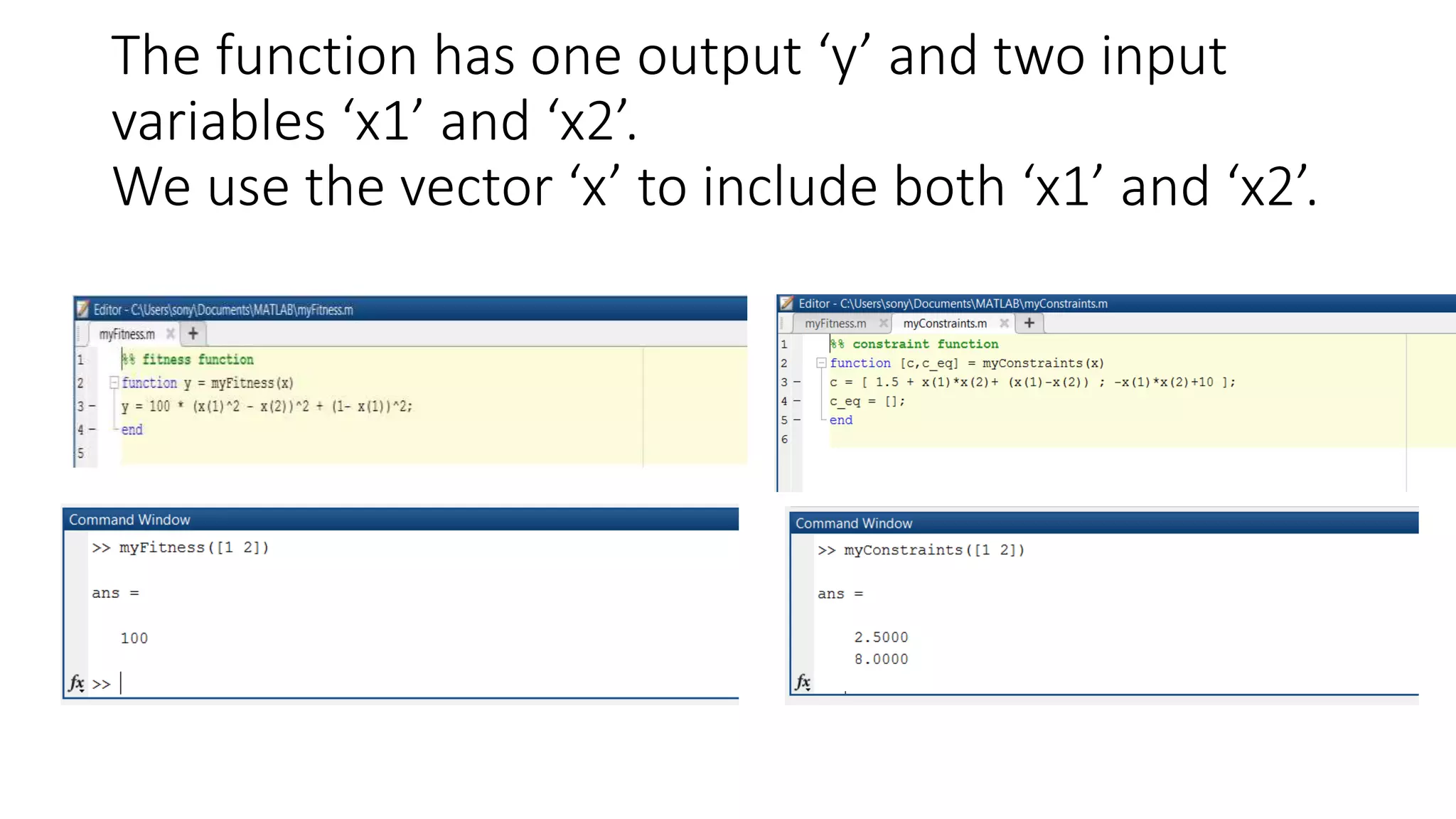
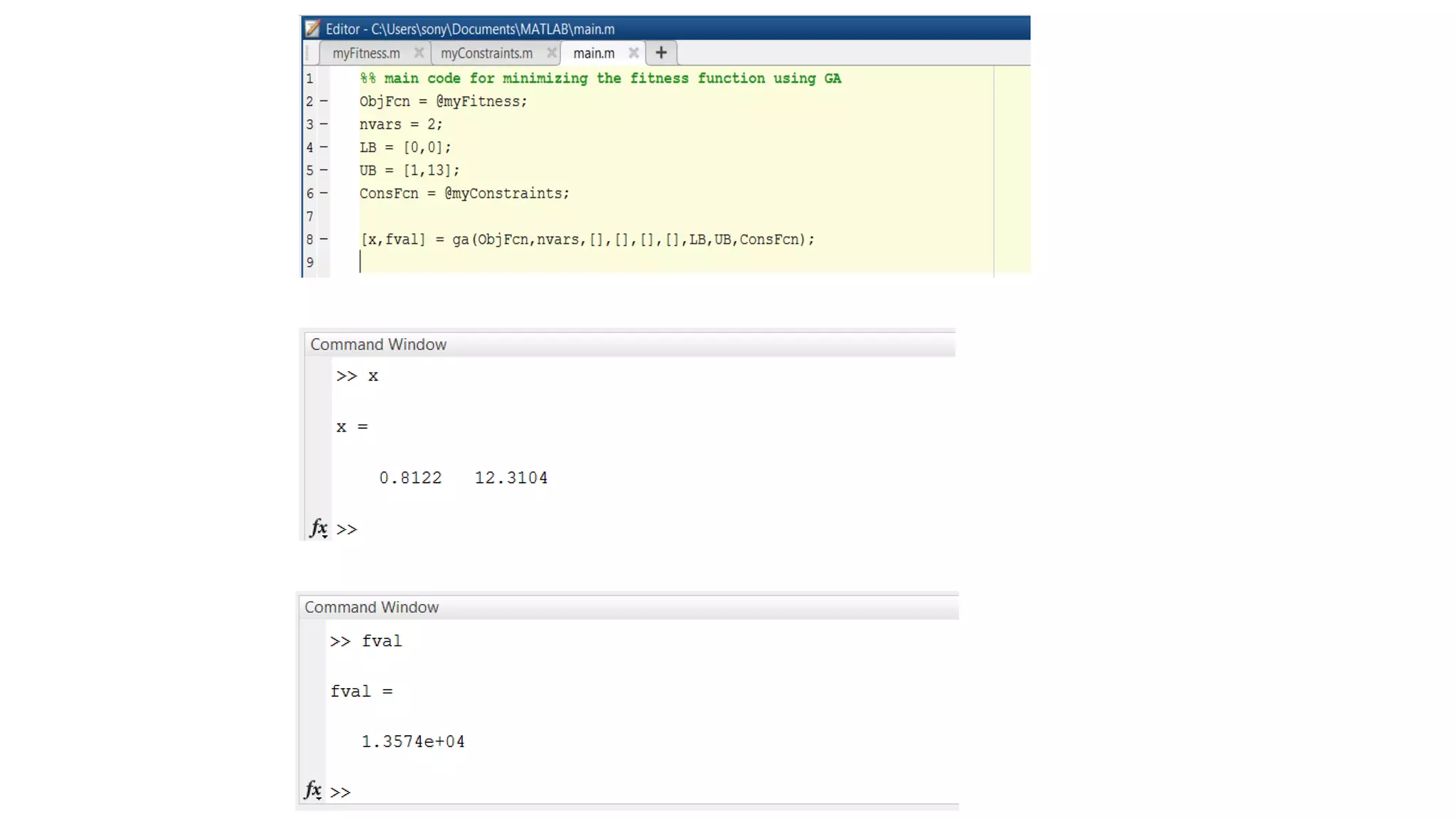
Genetic Algorithm

Genetic
Algorithm
by
Mrs Shimi S.L
Assistant Professor , EE
NITTTR, Chandigarh

Maxima and Minima from Calculus
•Great powers of calculus is in the determination of the
maximum or minimum value of a function.
•Take f(x) to be a function of x. Then the value of x for
which the derivative of f(x) with respect to x is equal
to zero corresponds to a maximum, a minimum or an
inflexion point of the function f(x).

• The height of a projectile that is fired straight up is given by the
motion equations

Classes of Search Techniques
Finonacci Newton
Direct methods Indirect methods
Calculus-based techniques
Evolutionarystrategies
Centralized Distributed
Parallel
Steady-state Generational
Sequential
Genetic algorithms
Evolutionary algorithms Simulated annealing
Guided random search techniques
Dynamic programming
Enumerative techniques
Search techniques

Genetic Algorithms is the most
commonly used prominent
computational algorithm introduced by
I. Rechenberg in 1960’s and developed
by John Holland in 1975. This
evolutionary algorithm mimics the
Darwin’s theory of evolution by natural
selection for problem solving.

Simple Genetic Algorithm
{
initialize population;
evaluate population;
while Termination Criteria Not Satisfied
{
select parents for reproduction;
perform crossover and mutation;
evaluate population;
}
}

The GA Cycle of Reproduction
reproduction
population evaluation
modification
discard
deleted
members
parents
children
modified
children
evaluated children

Population
Chromosomes could be:
• Bit strings (0101 ... 1100)
• Real numbers (43.2 -33.1 ... 0.0 89.2)
• Permutations of element (E11 E3 E7 ... E1 E15)
• Lists of rules (R1 R2 R3 ... R22 R23)
• Program elements (genetic programming)
• ... any data structure ...
population

Population Size
Population size depicts the number of
chromosomes in one generation. If the population
size is very small, then only a small part of the
search space is explored. Whereas, if the
population size is too large then a very large part of
the search space is explored and due to obvious
reasons the algorithm slows down.

Selection
• Best chromosomes are selected from the population to form the
parents for next generation
• The different selection methods for choosing the best chromosomes
are
(i) Roulette Wheel Selection,
(ii) Tournament Selection,
(iii) Rank Selection,
(iv) Boltzman Selection,
(v) Steady-State Selection, etc.

Roulette Wheel Selection
Better chromosomes have high probability to be selected as new
parents. The probability of each individual chromosome getting
selected is given by the equation.
𝑃𝑖 =
𝑓 𝑖
𝑗=1
𝑁 𝑓 𝑖
where,
fi is the fitness of the individual i in the population
N is the number of individuals in the population

Reproduction
reproduction
population
parents
children
Parents are selected at random with selection chances biased
in relation to chromosome evaluations.

Chromosome Modification
modification
children
• Modifications are stochastically triggered
• Operator types are:
• Crossover (recombination)
• Mutation
modified children

Crossover: Recombination
Single point crossover

Arithmetic Crossover
Crossover is a critical feature of genetic algorithms:
•It greatly accelerates search early in evolution of a
population
•It leads to effective combination of schemata
(subsolutions on different chromosomes)

Mutation: Local Modification
Before: (1 0 1 1 0 1 1 0)
After: (0 1 1 0 0 1 1 0)
Before: (1.38 -69.4 326.44 0.1)
After: (1.38 -67.5 326.44 0.1)
• Causes movement in the search space
(local or global)
• Restores lost information to the population

Exploration: Discovering promising areas in the search space, i.e.
gaining information on the problem
Exploitation: Optimising within a promising area, i.e. using
information
There is co-operation and competition between them
• Crossover is explorative, it makes a big jump to an area
somewhere “in between” two (parent) areas
• Mutation is exploitative, it creates random small diversions,
thereby staying near (in the area of ) the parent
Crossover OR mutation?

• Only crossover can combine information from two parents
• Only mutation can introduce new information (alleles)
• Crossover does not change the allele frequencies of the
population
• To hit the optimum you often need a ‘lucky’ mutation
Crossover OR mutation?

Evaluation
• The evaluator decodes a chromosome and assigns it a fitness
measure
• The evaluator is the only link between a classical GA and the problem
it is solving
evaluation
evaluated
children
modified
children

Deletion
• Generational GA:
entire populations replaced with each iteration
• Steady-state GA:
a few members replaced each generation
population
discard
discarded members

Termination
This evolutionary process is continued until the
termination condition is satisfied. The termination
conditions may be:
• Reaching the maximum number of generations
• Successive iteration does not provide proper results
• An optimal fitness value of the population is reached.

TSP Example: 30 Cities
0
20
40
60
80
100
120
0 10 20 30 40 50 60 70 80 90 100
y
x

Solution i (Distance = 941)
0
20
40
60
80
100
120
0 10 20 30 40 50 60 70 80 90 100
y
x
TSP30 (Performance = 941)

Solution j(Distance = 800)
0
10
20
30
40
50
60
70
80
90
100
0 10 20 30 40 50 60 70 80 90 100
x
y

Solution k(Distance = 652)
0
20
40
60
80
100
120
0 10 20 30 40 50 60 70 80 90 100
y
x

Best Solution (Distance = 420)
42
38
35
26
21
35
32
7
38
46
44
58
60
69
76
78
71
69
67
62
84
94
0
20
40
60
80
100
120
0 10 20 30 40 50 60 70 80 90 100
y
x
TSP30 Solution (Performance = 420)

Overview of Performance
0
200
400
600
800
1000
1200
1400
1600
1800
1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31
D
is
ta
n
c
e
Generations (1000)
TSP30 - Overview of Performance
Best
Worst
Average

Consider the problem of maximizing the function,
f(x) = x2
Where x is permitted to vary between 0 to 31.
(i) 0(00000) and 31(11111) code x into finite
length string
(ii) Select initial population at random (size 4)
(iii) Calculate fitness value for all strings
(iv) probability of selection by:
𝑃𝑟𝑜𝑏𝑖=
𝑓(𝑥) 𝑖
𝑖=1
𝑛
𝑓(𝑥) 𝑖
,

Table 1. Selection
String
No.
Initial
population
X
Value
Fitness
value
Prob. %age
Prob.
Expected
Count
Actual
Count
1. 01100 12 144 0.1247 12.47% 0.4987 1
2. 11001 25 625 0.5411 54.11% 2.1645 2
3. 00101 5 25 0.0216 2.16% 0.0866 0
4. 10011 19 361 0.3126 31.26% 1.2502 1
Sum
Avg.
Max.
1155
288.75
625
1.0000
0.2500
0.5411
100%
25%
54.11%
4.0000
1.0000
2.1645

Table 2. Crossover
String
No.
Mating
Pool
Crossover
point
Offspring
after
crossover
X value Fitness
value
1. 01100 4 01101 13 169
2. 11001 4 11000 24 576
3. 11001 3 11011 27 729
4. 10011 3 10001 17 289
Sum
Avg.
Max.
1763
440.75
729

Table 3. Mutation
String
No.
Offspring
After
crossover
Mutation
chromosomes
Offspring
after
mutation
X value Fitness
value
1. 01101 10000 11101 29 841
2. 11000 00000 11000 24 576
3. 11011 00000 11011 27 729
4. 10001 00100 10101 20 400
Sum
Avg.
Max.
2546
636.5
841

Minimize the following fitness function
including 2 variables:
𝒎𝒊𝒏 𝒙 𝒇 𝒙 = 𝟏𝟎𝟎(𝒙 𝟏
𝟐
− 𝒙 𝟐) 𝟐
+ (𝟏 − 𝒙 𝟏) 𝟐
Subject to the following linear constraints and
bounds:
𝑥1 𝑥2 + 𝑥1 − 𝑥2 + 1.5 ≤ 0
10 − 𝑥1 𝑥2 ≤ 0
0 ≤ 𝑥1 ≤ 1 and 0 ≤ 𝑥2 ≤ 13

The function has one output ‘y’ and two input
variables ‘x1’ and ‘x2’.
We use the vector ‘x’ to include both ‘x1’ and ‘x2’.

Advantages of Genetic Algorithm
 Parallelism, robustness and liability
 Solution space is wider
 Handles large, poorly understood search spaces easily
 Easily modified for different problems
 Easy to discover global optimum
 Handles noisy functions as well
 Only uses function evaluations
 They require no information about the response surface
 Perform very well for large-scale optimization problems
 Can be employed for a wide variety of optimization problems
 The problem has multi objective function
 Very robust to difficulties in the evaluation of the objective function

Limitations of Genetic Algorithm
 The problem of identifying fitness function
 Requires large number of fitness function evaluations
 The problem of choosing the various parameters like
the size of the population, mutation rate, crossover
rate, the selection method and its strength.
 Definition of representation of the problem
 No effective terminator
 Needs to be coupled with a local search technique
 Have trouble finding the exact global optimum

Genetic Algorithm

More Related Content

What's hot

Viewers also liked

Similar to Genetic Algorithm

More from SHIMI S L

Recently uploaded

In this document

Genetic Algorithm