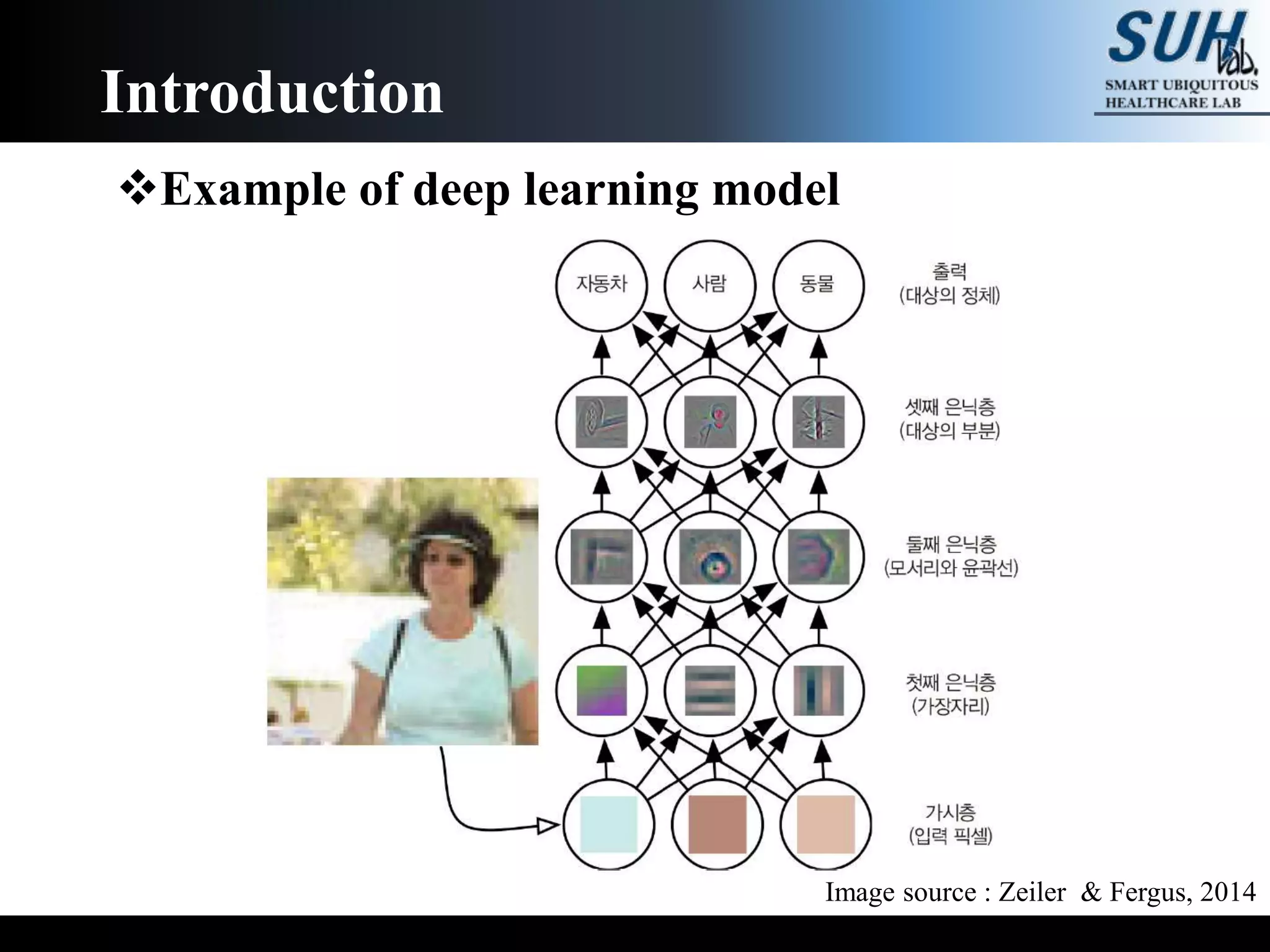
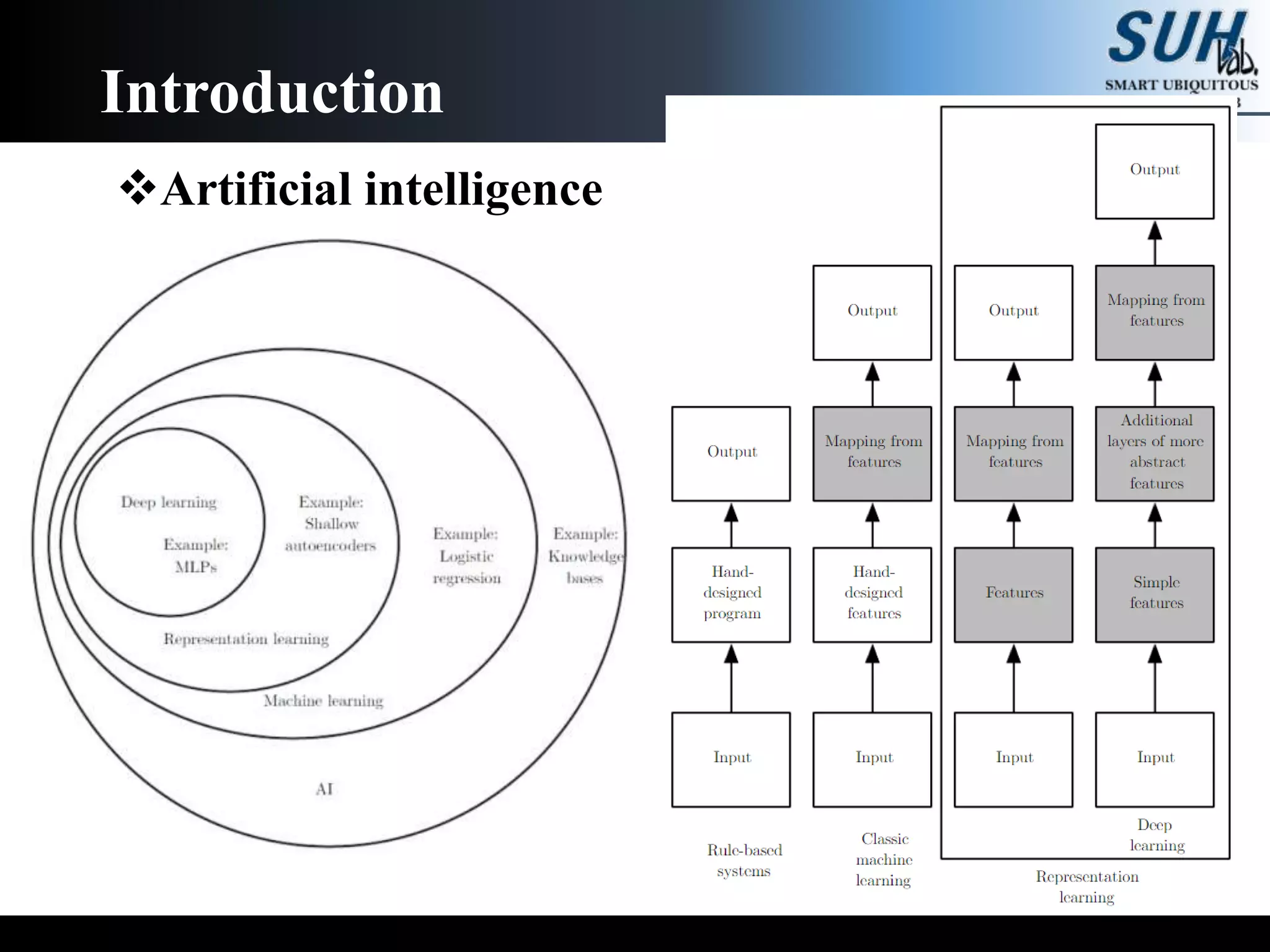
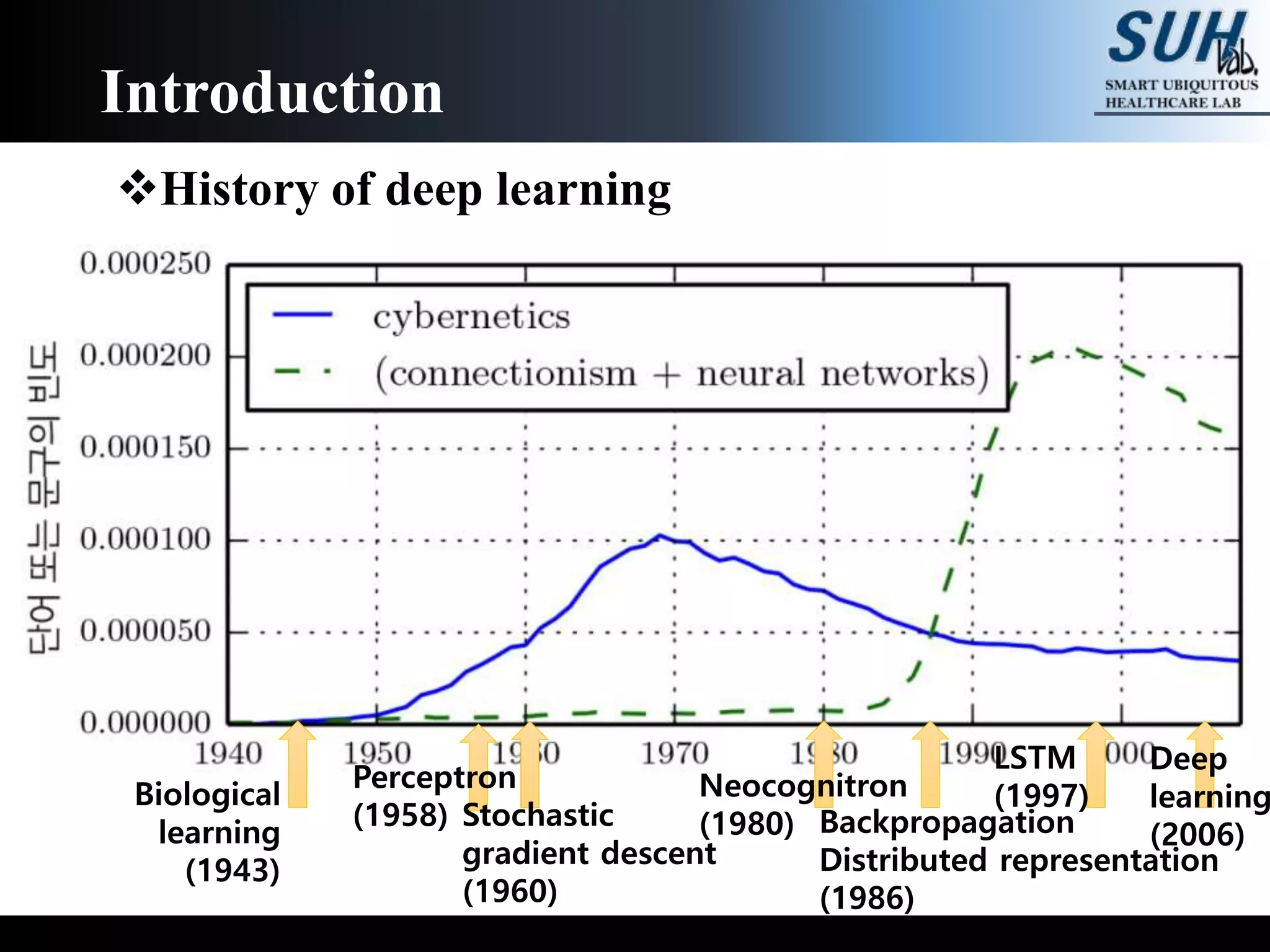
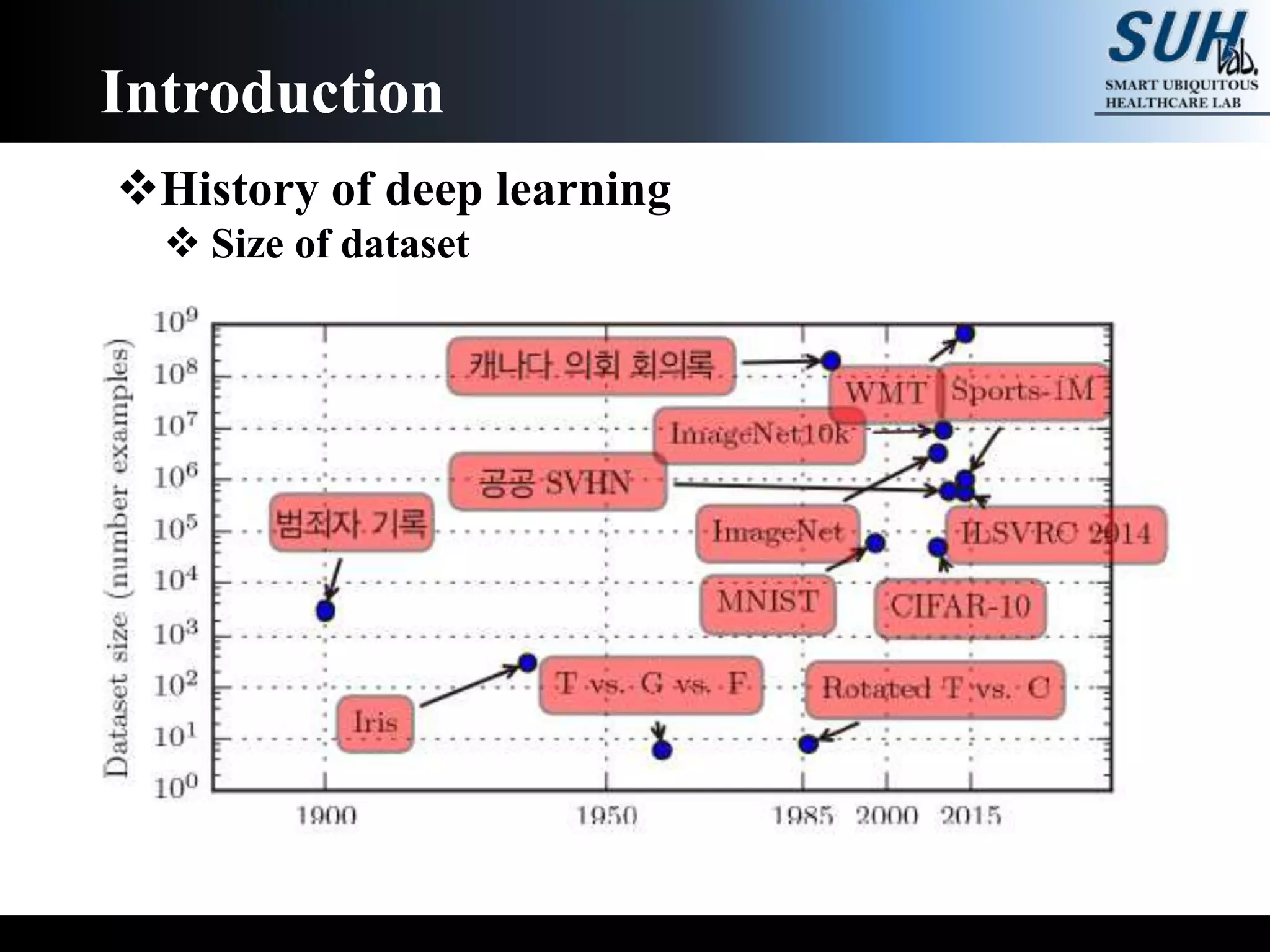
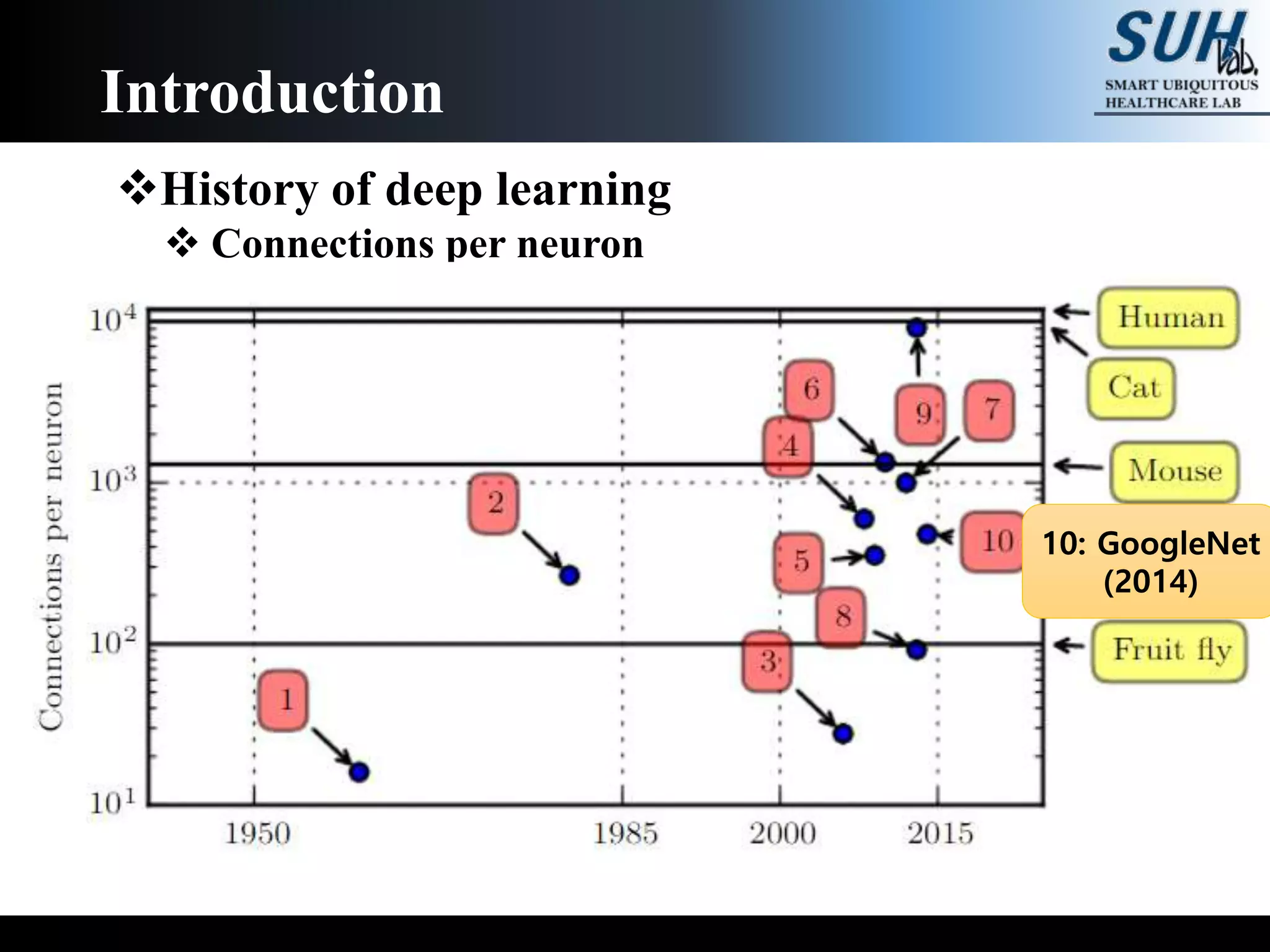
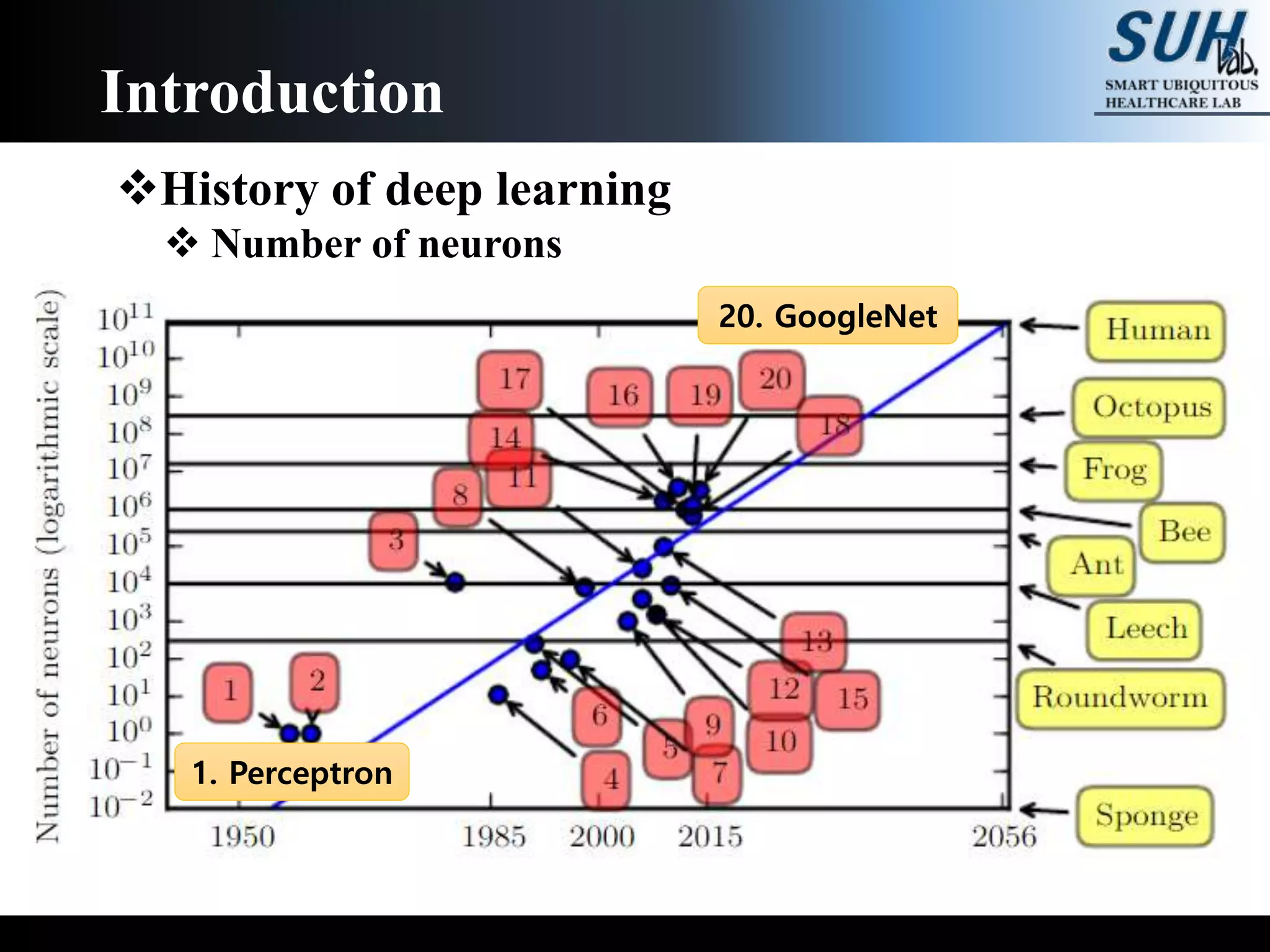
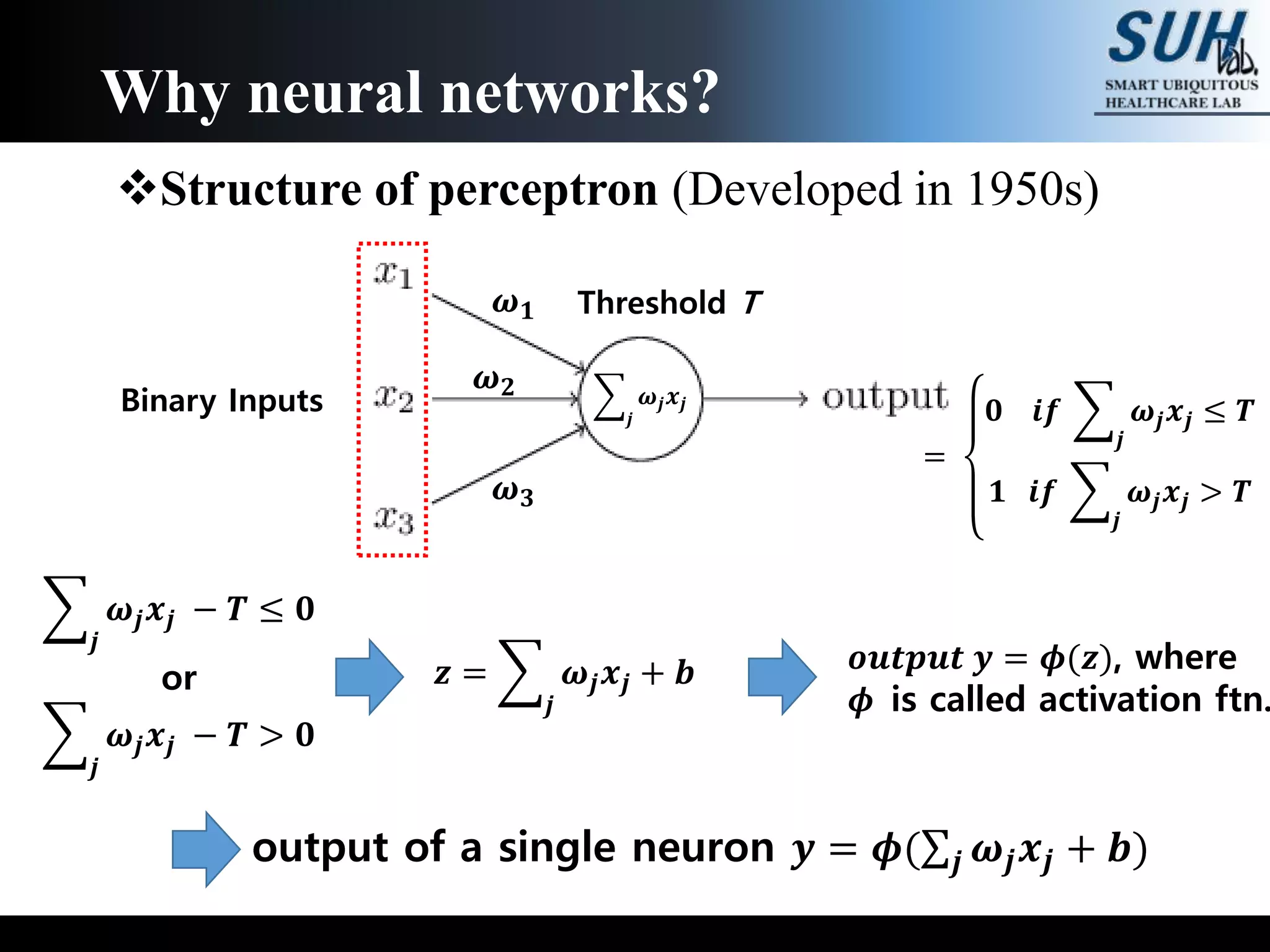
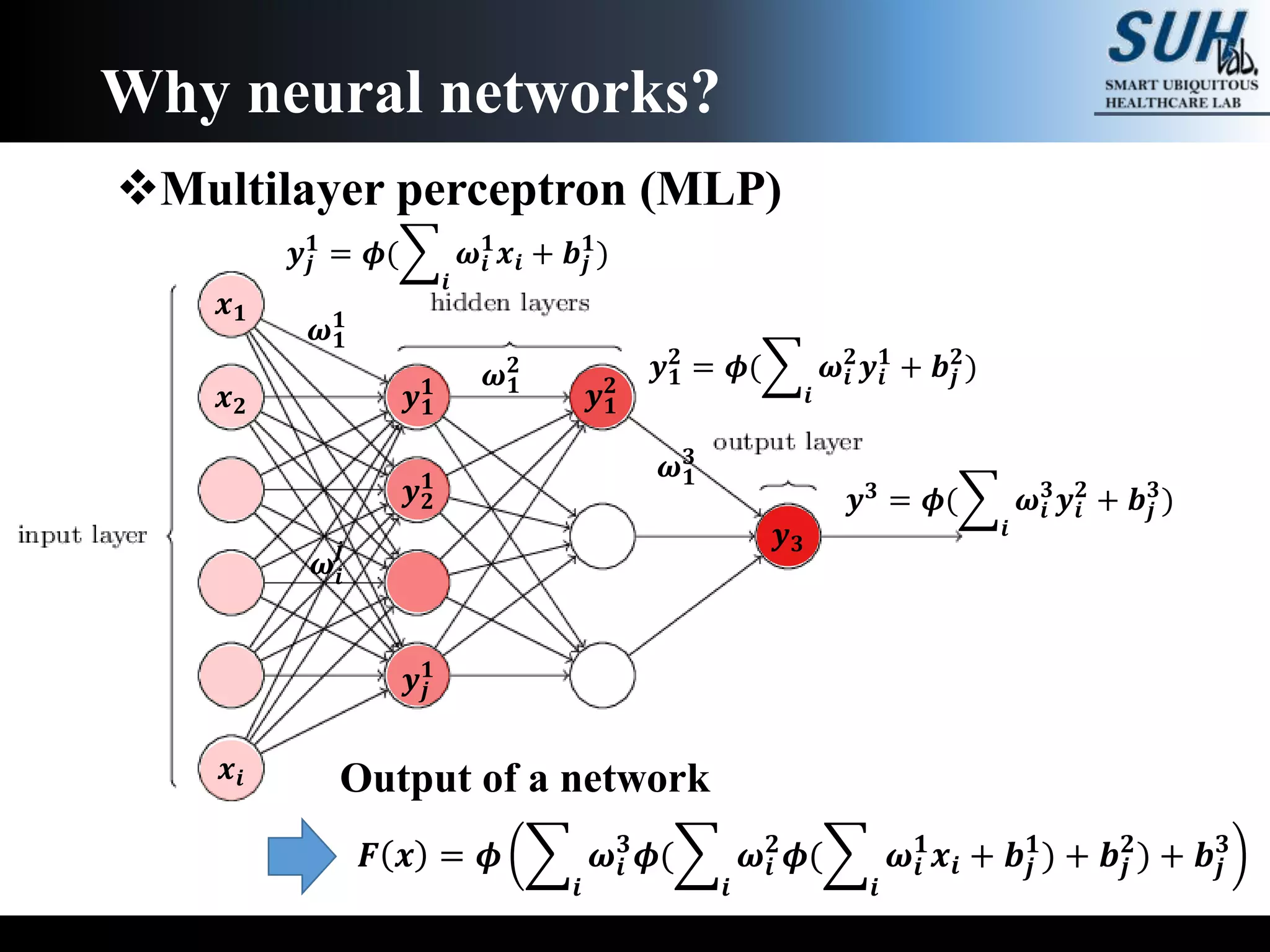
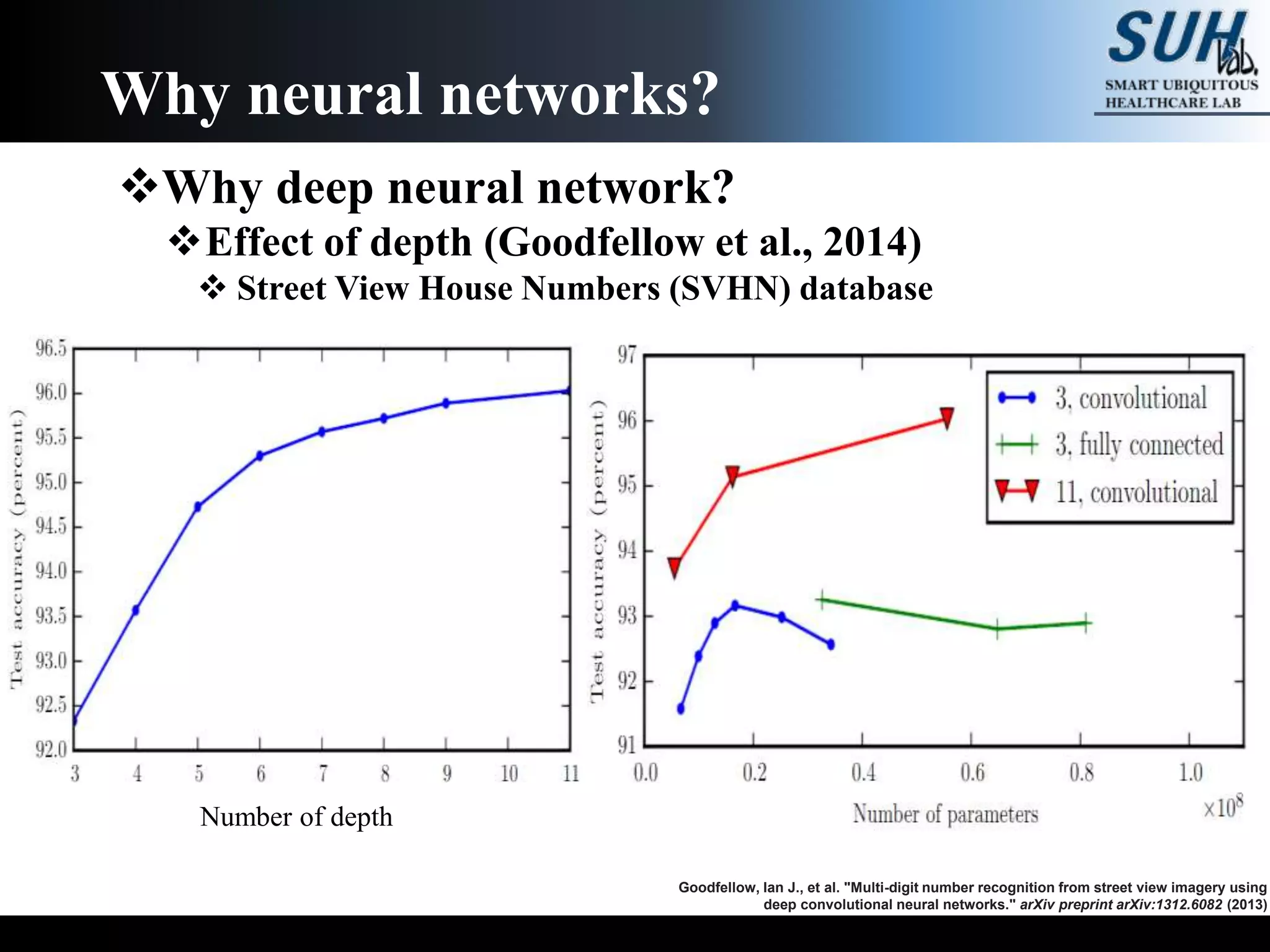
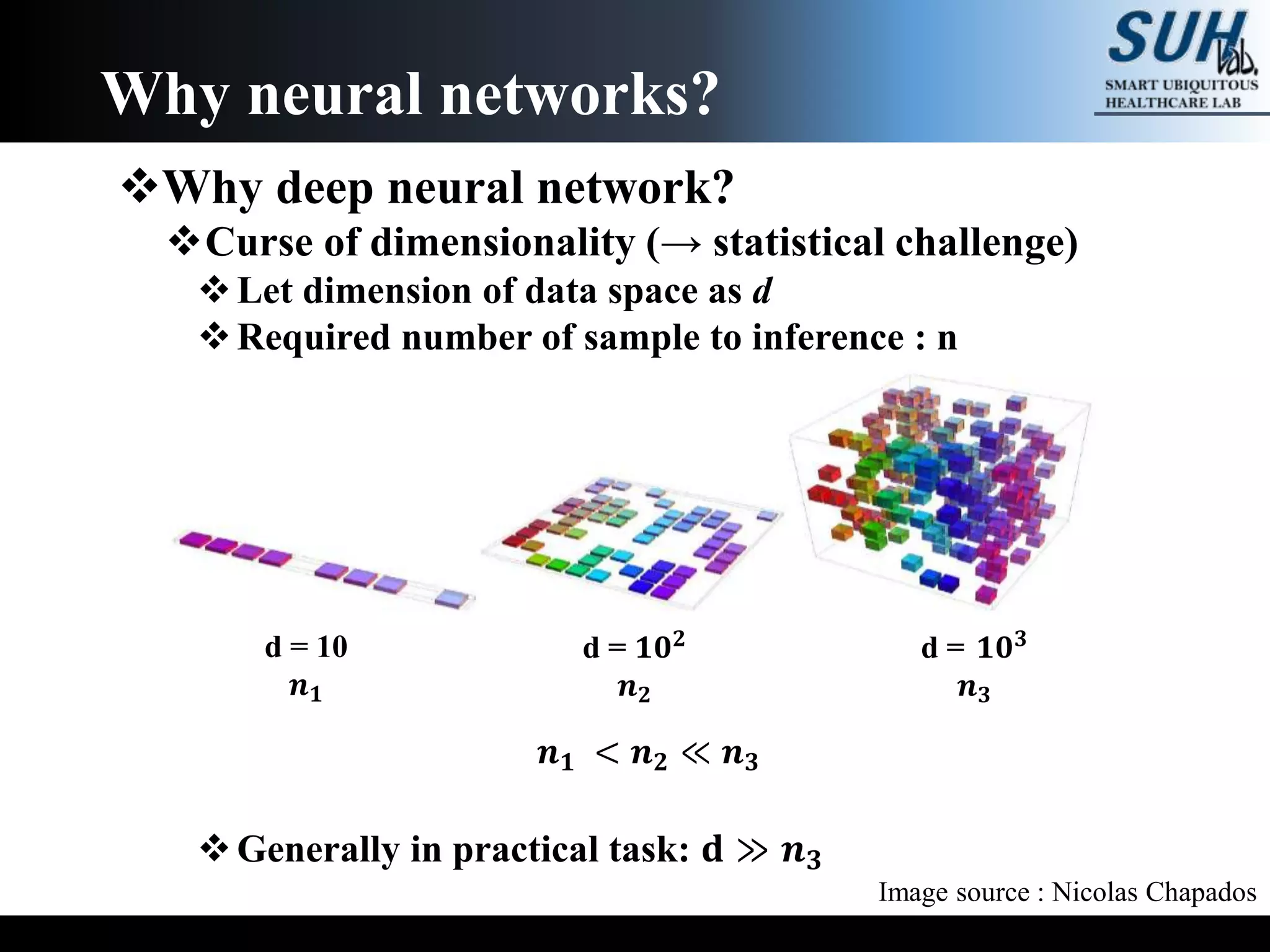
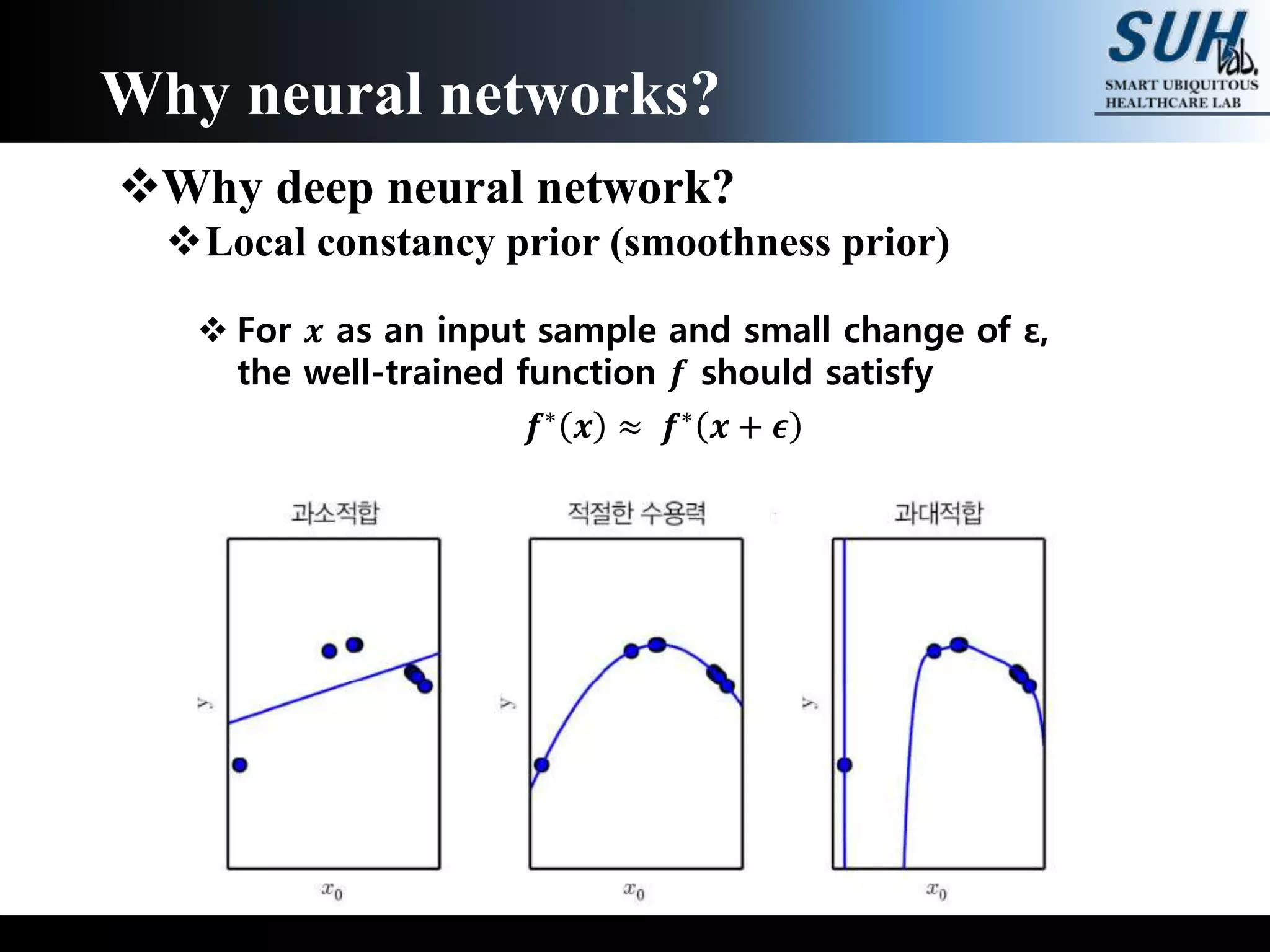
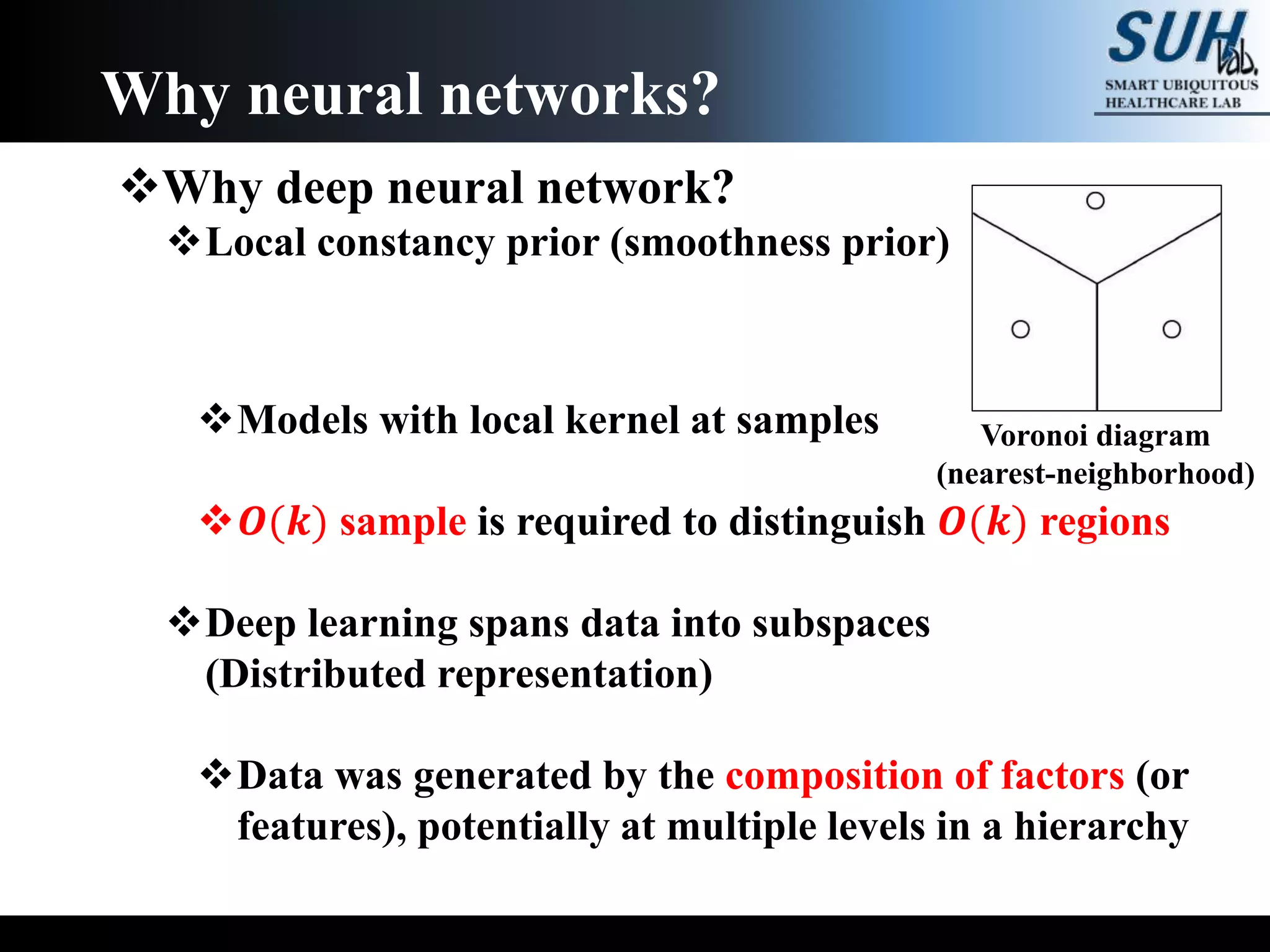
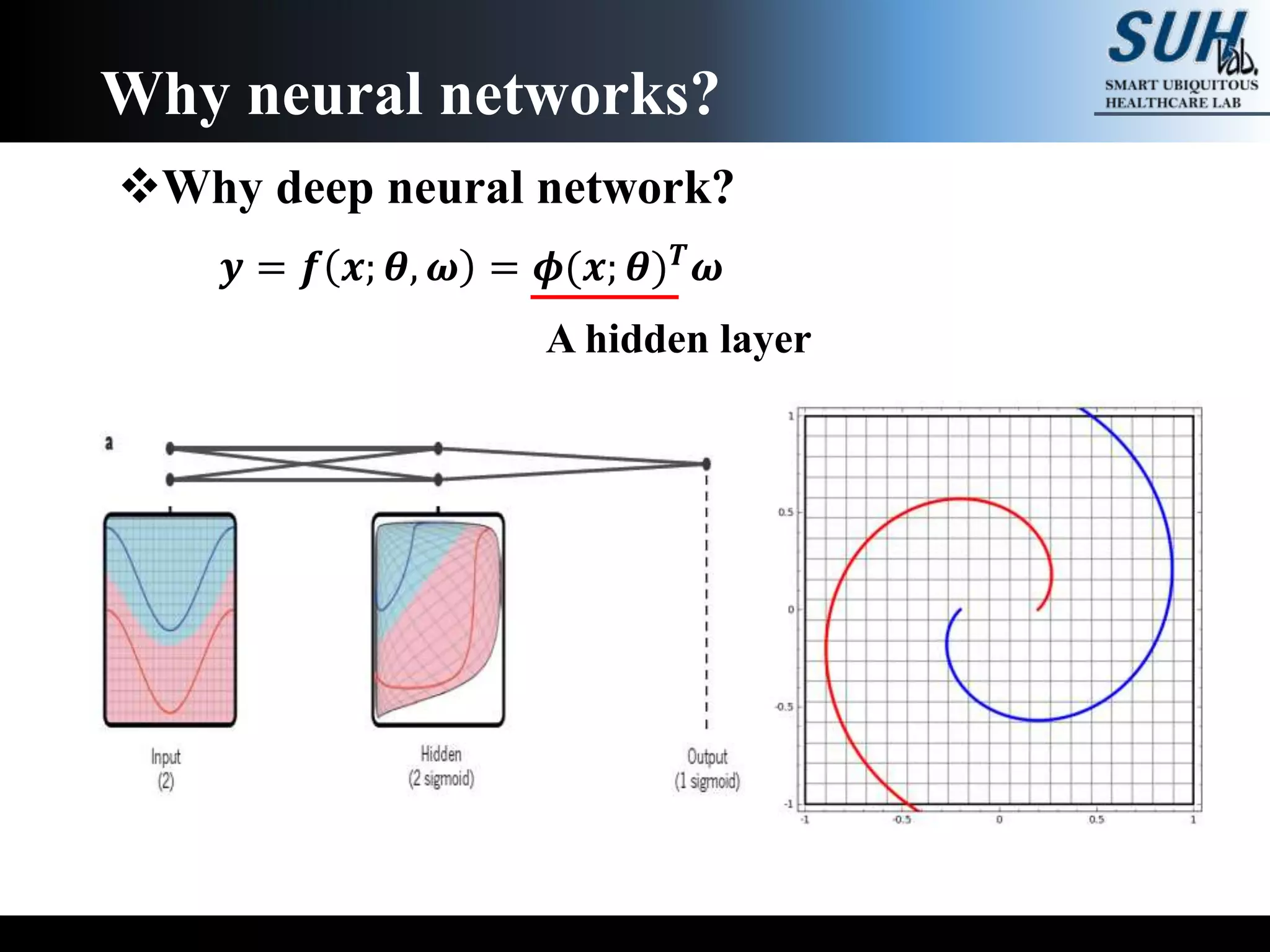
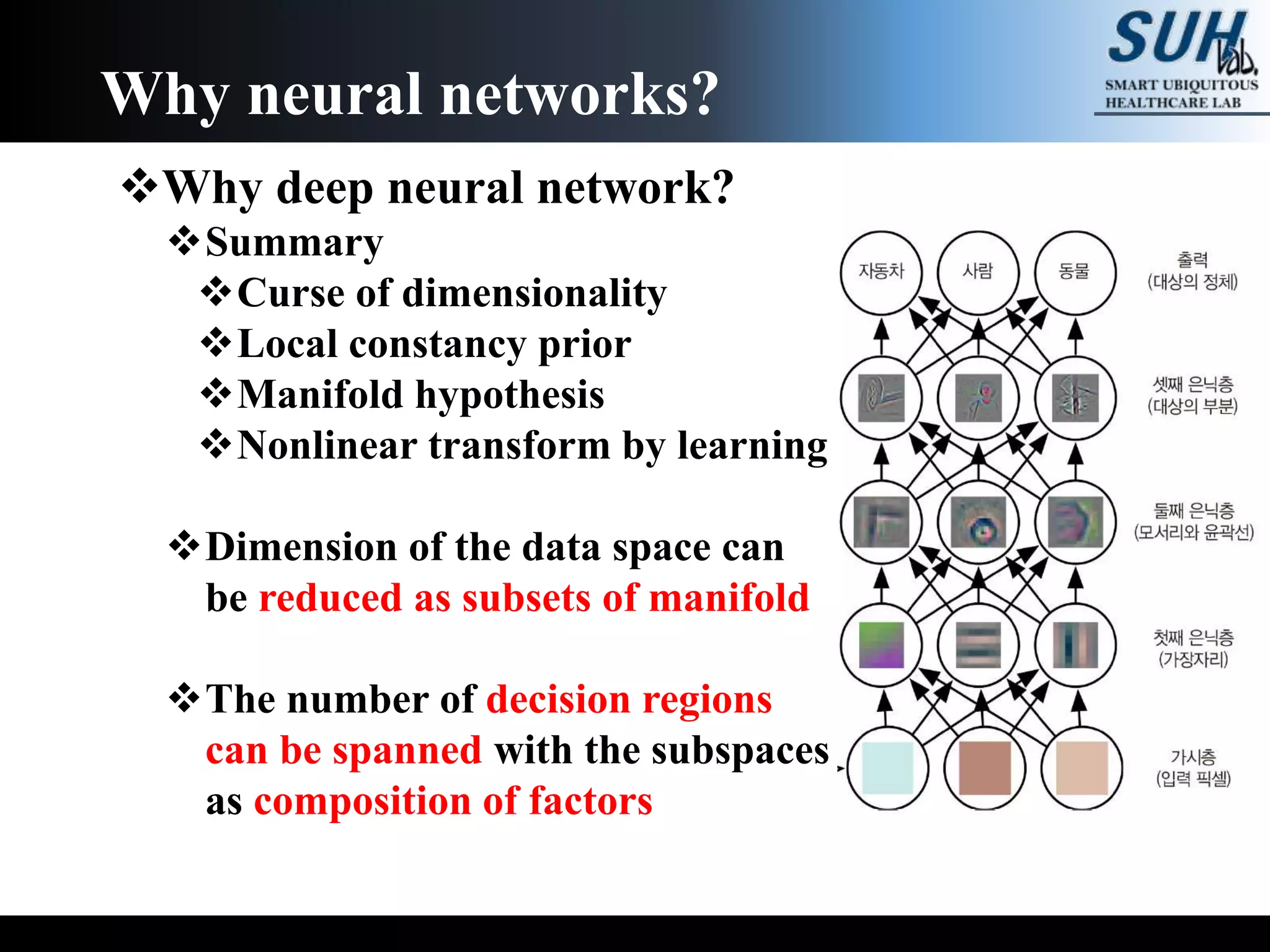
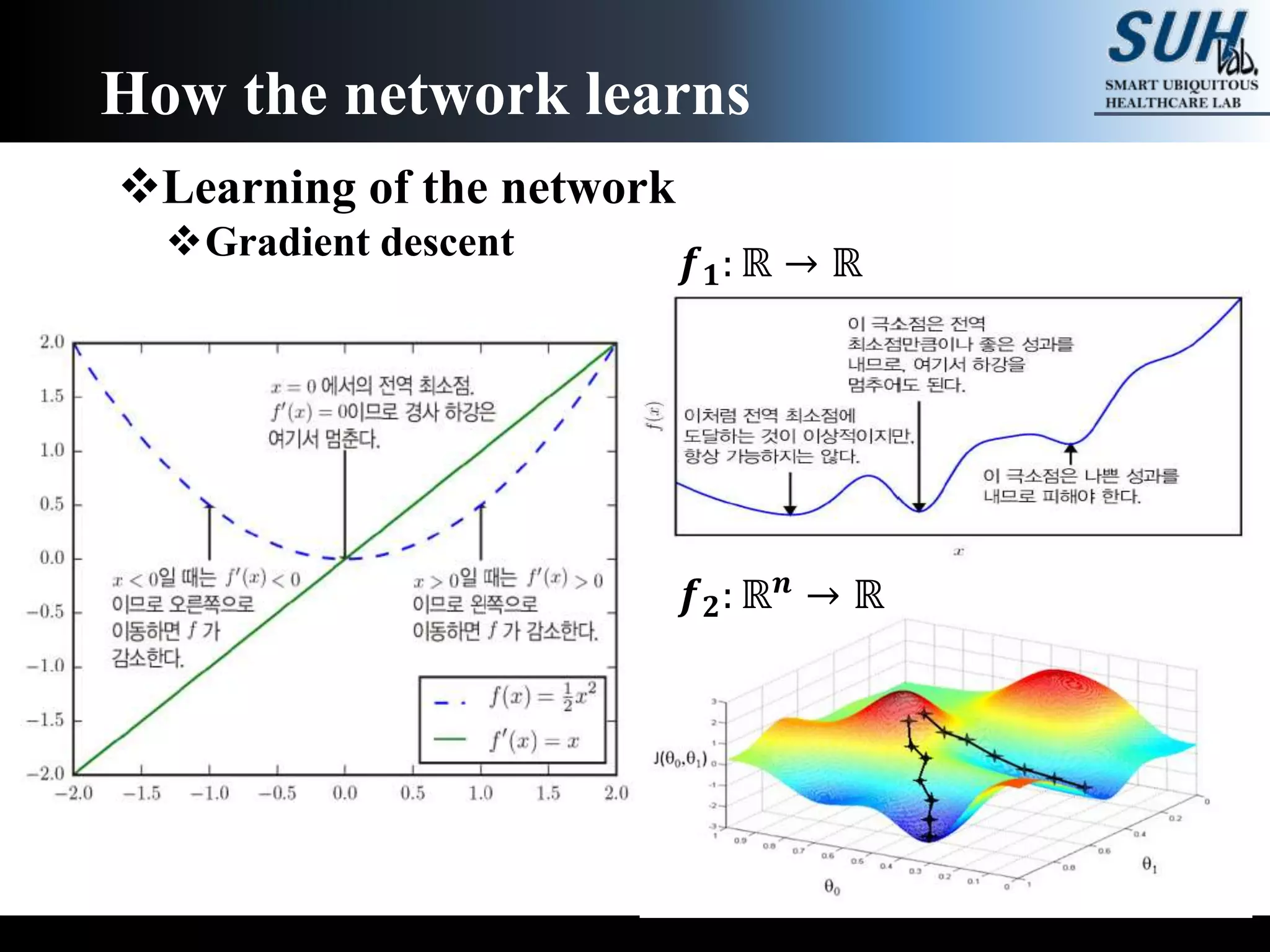
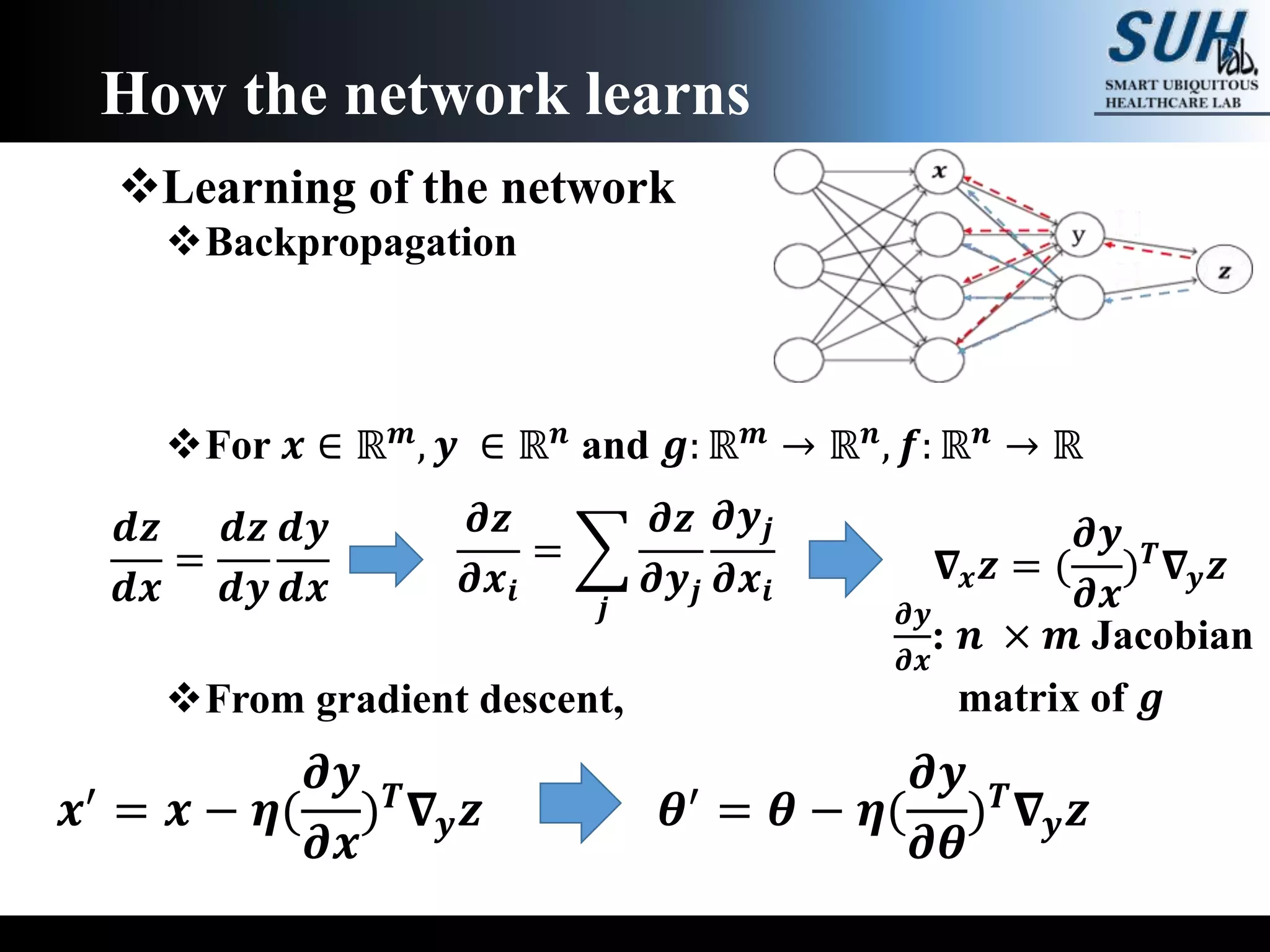
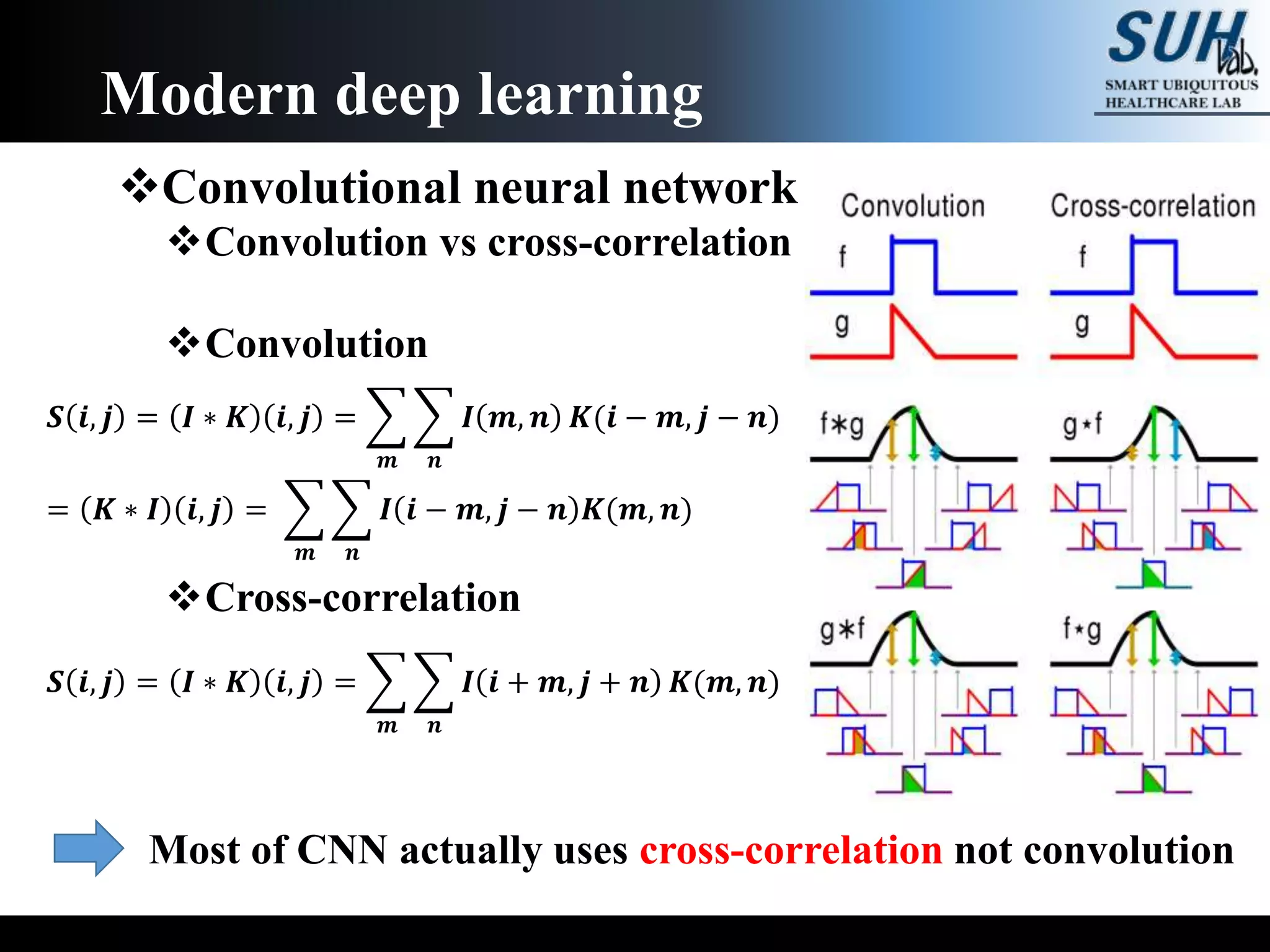
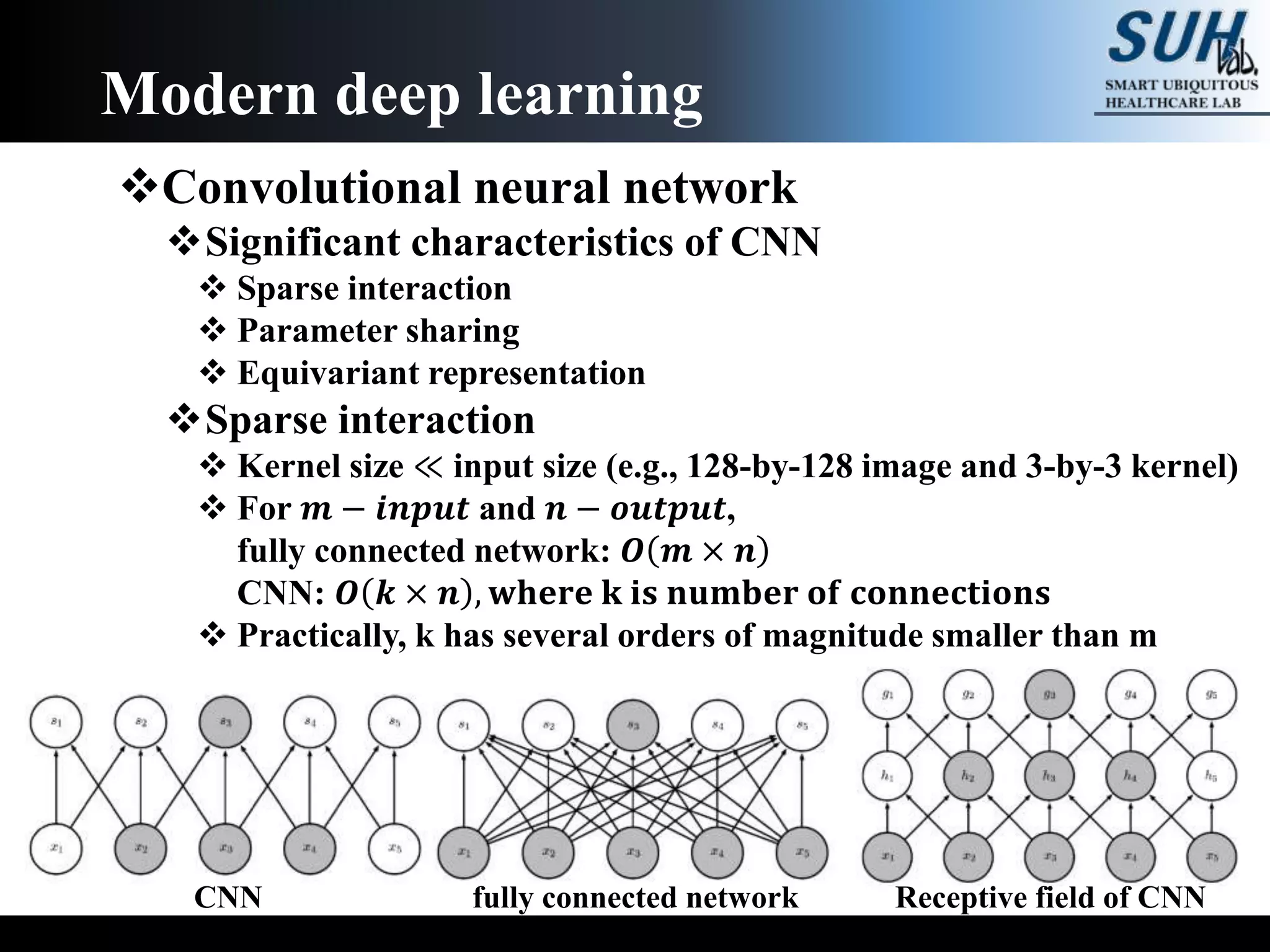
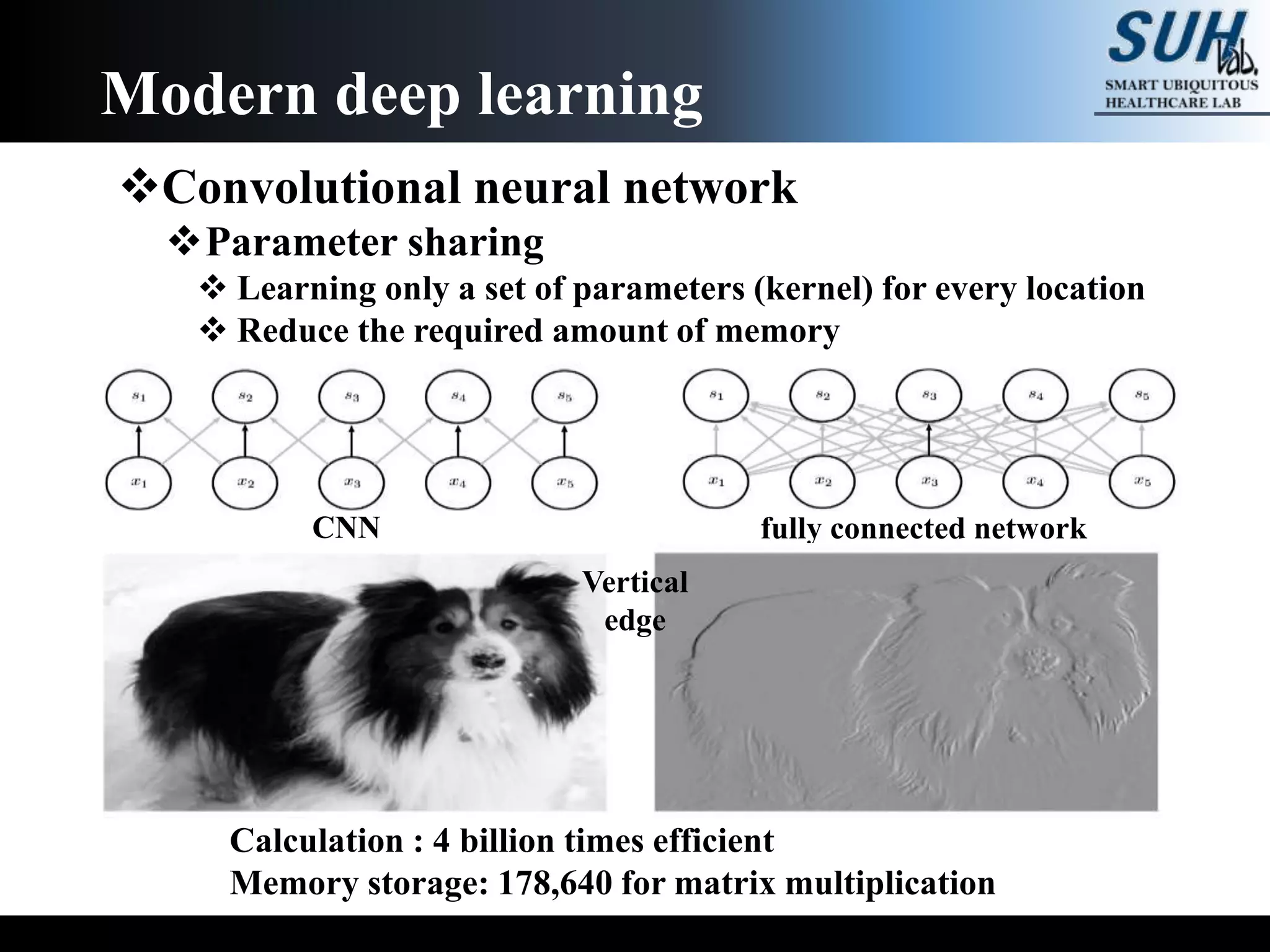
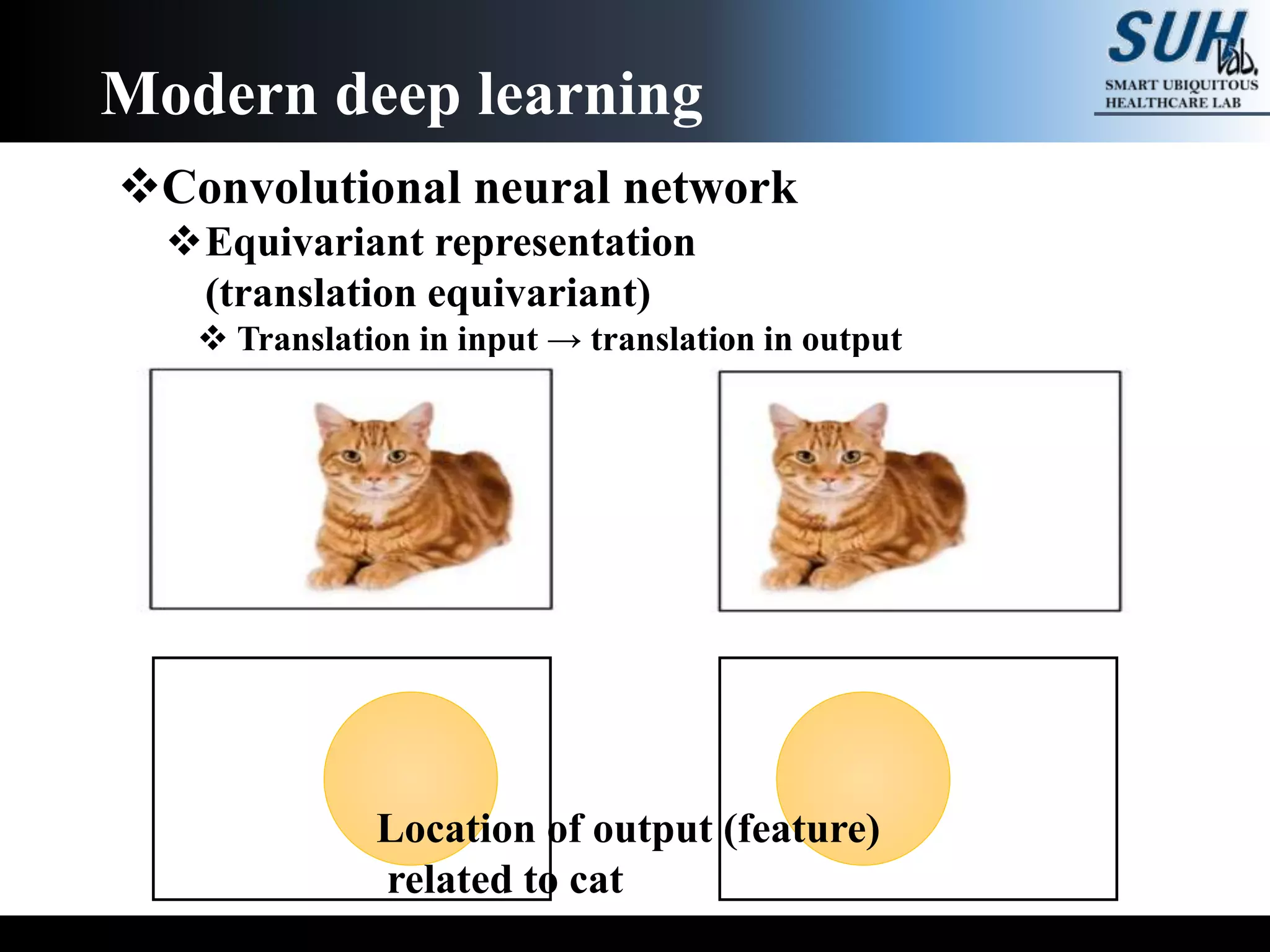
The document is a lecture on deep learning discussing its fundamentals, including neural networks, learning mechanisms like gradient descent and backpropagation, and modern architectures such as convolutional and recurrent neural networks. It delves into the historical context, explaining concepts like the universal approximation theorem and challenges related to dimensionality. Finally, it highlights the significance of deep learning in artificial intelligence and practical applications.