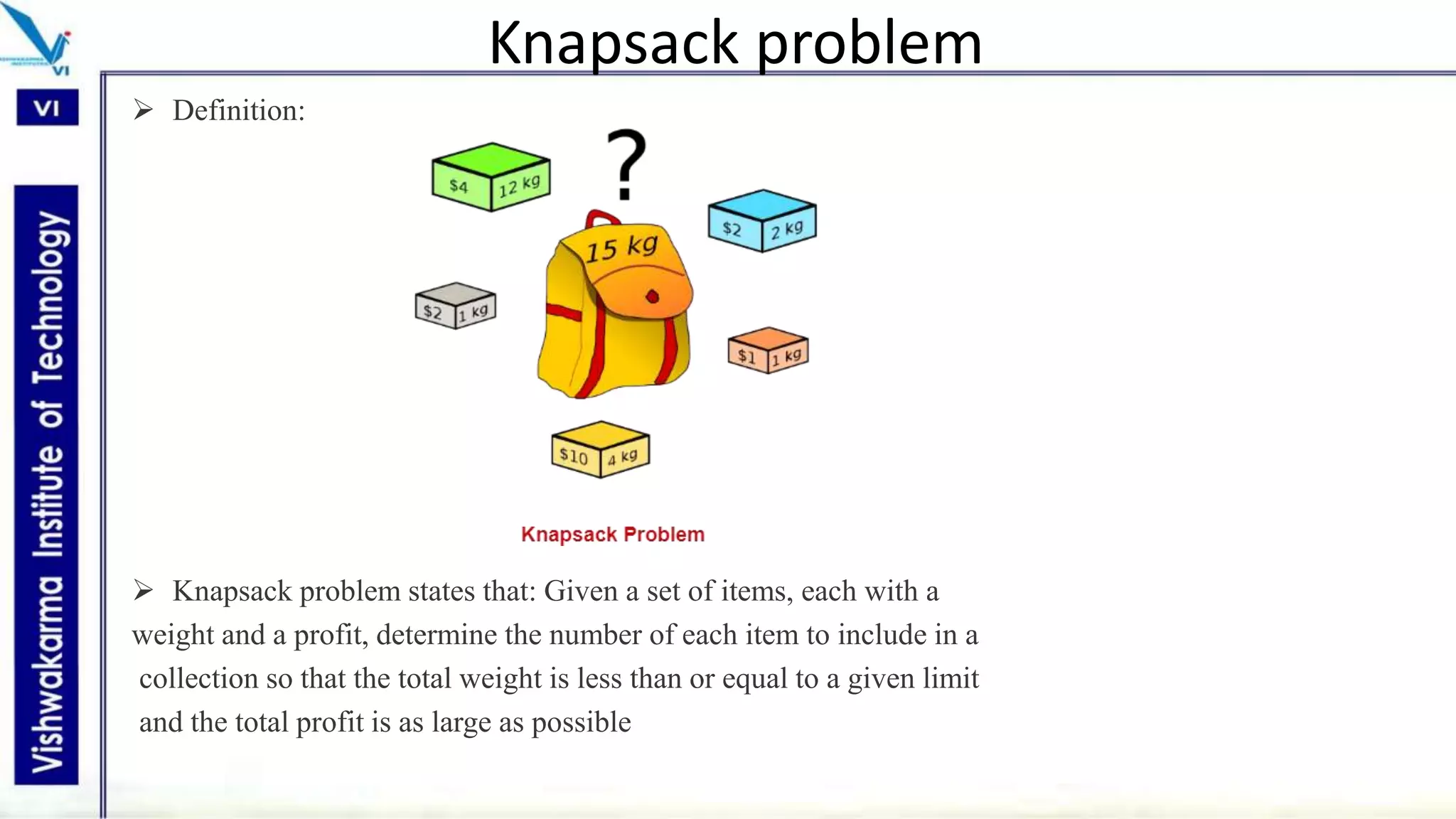
The document discusses the knapsack problem and greedy algorithms, detailing their definitions, properties, and applications. It presents two versions of the knapsack problem: the 0/1 knapsack, solved using dynamic programming, and the fractional knapsack, which utilizes the greedy approach. Additionally, it includes examples, algorithms, complexities, and real-world applications related to knapsack problems.









![Algorithm and complexity of 0/1 knapsack
Knapsack_DP(n,W)
1. for w = 1 to m
2. do B[0,w] 0
3. for i = 1 to n
4. do B[i,0] 0
5. for w = 1 to m
6. do if (Wi < = w && B[i-1,w-Wi] +bk > B[i-1,w]
7. then B[i,w] B[i-1,w-Wi]+bk
8. else B[i,w] B[i-1,w]
Complexity:
Clearly the dynamic programming algorithm for the knapsack problem has a time complexity of O(n.w) .
Where , n= the number of items & w= the capacity of the knapsack.](https://image.slidesharecdn.com/daappt1-211125081504/75/Knapsack-problem-using-greedy-approach-11-2048.jpg)


