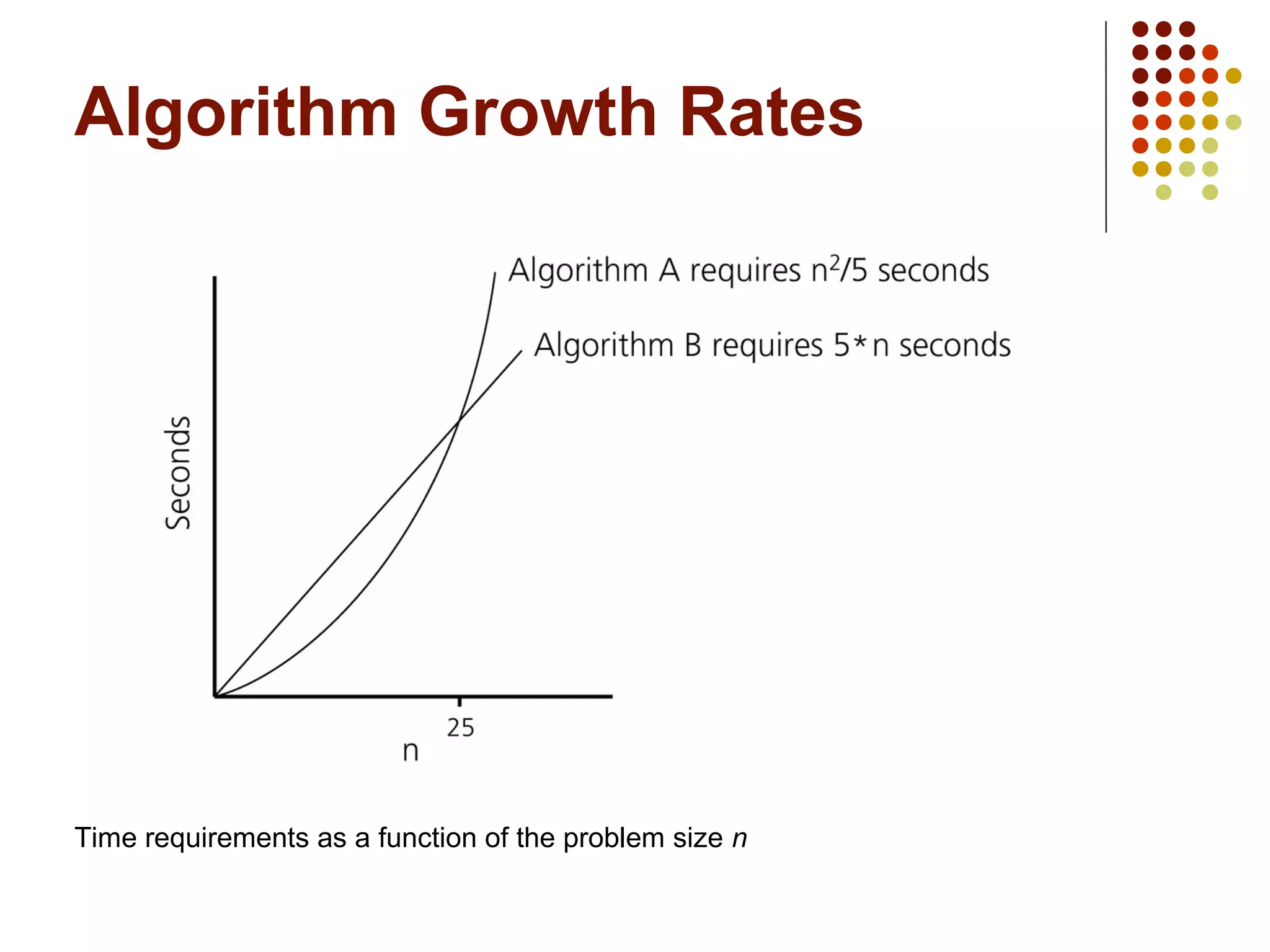
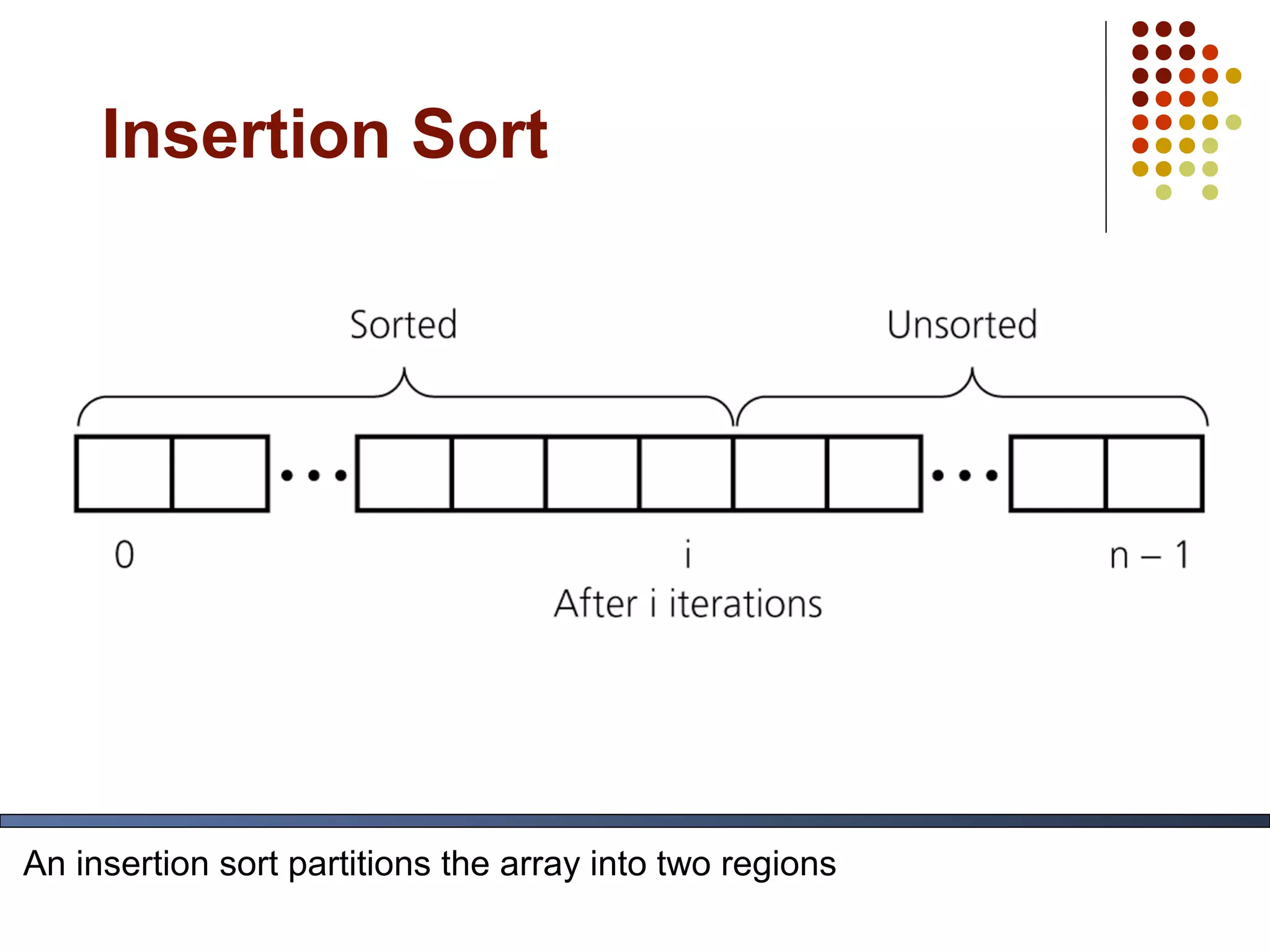
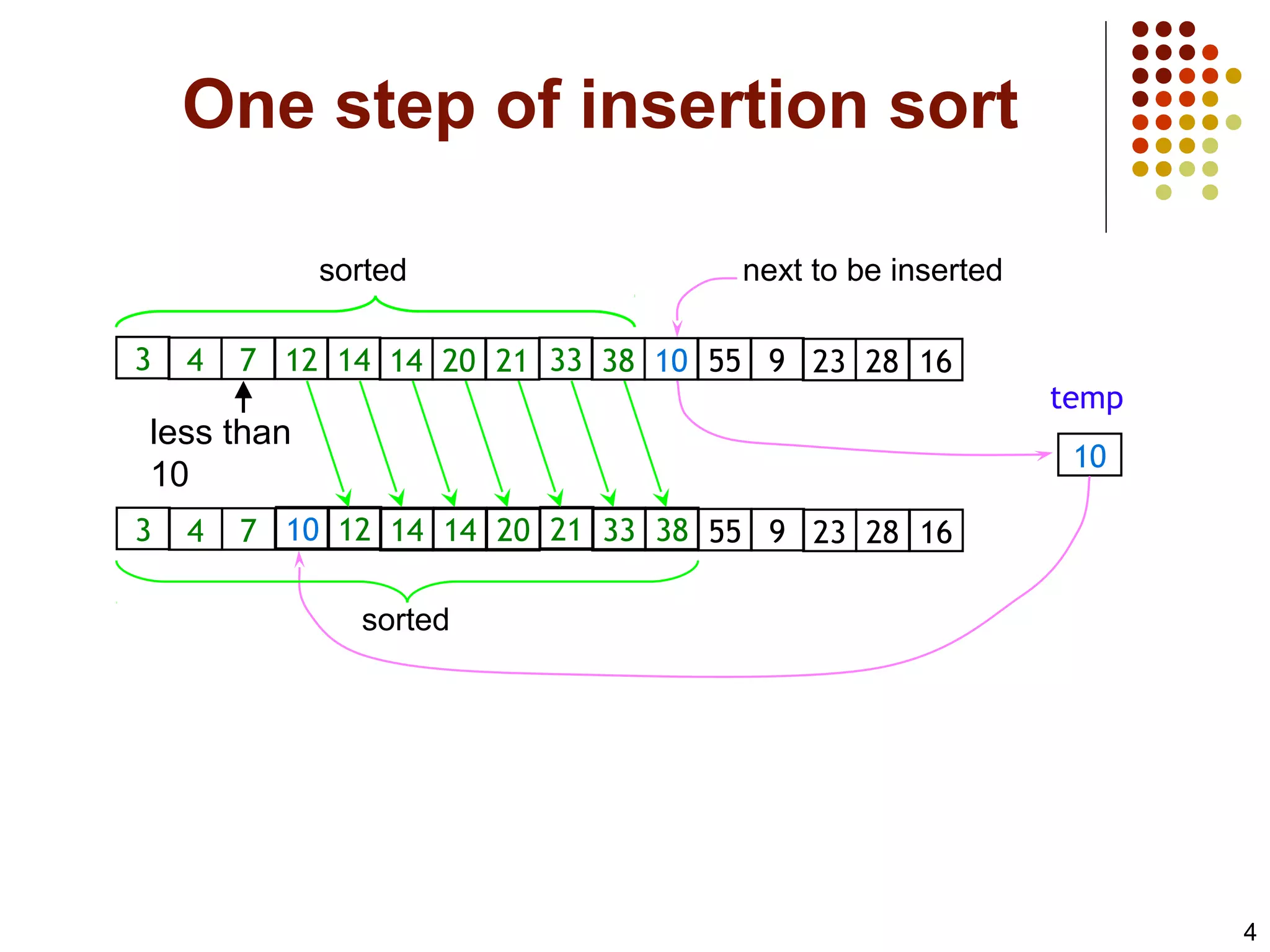
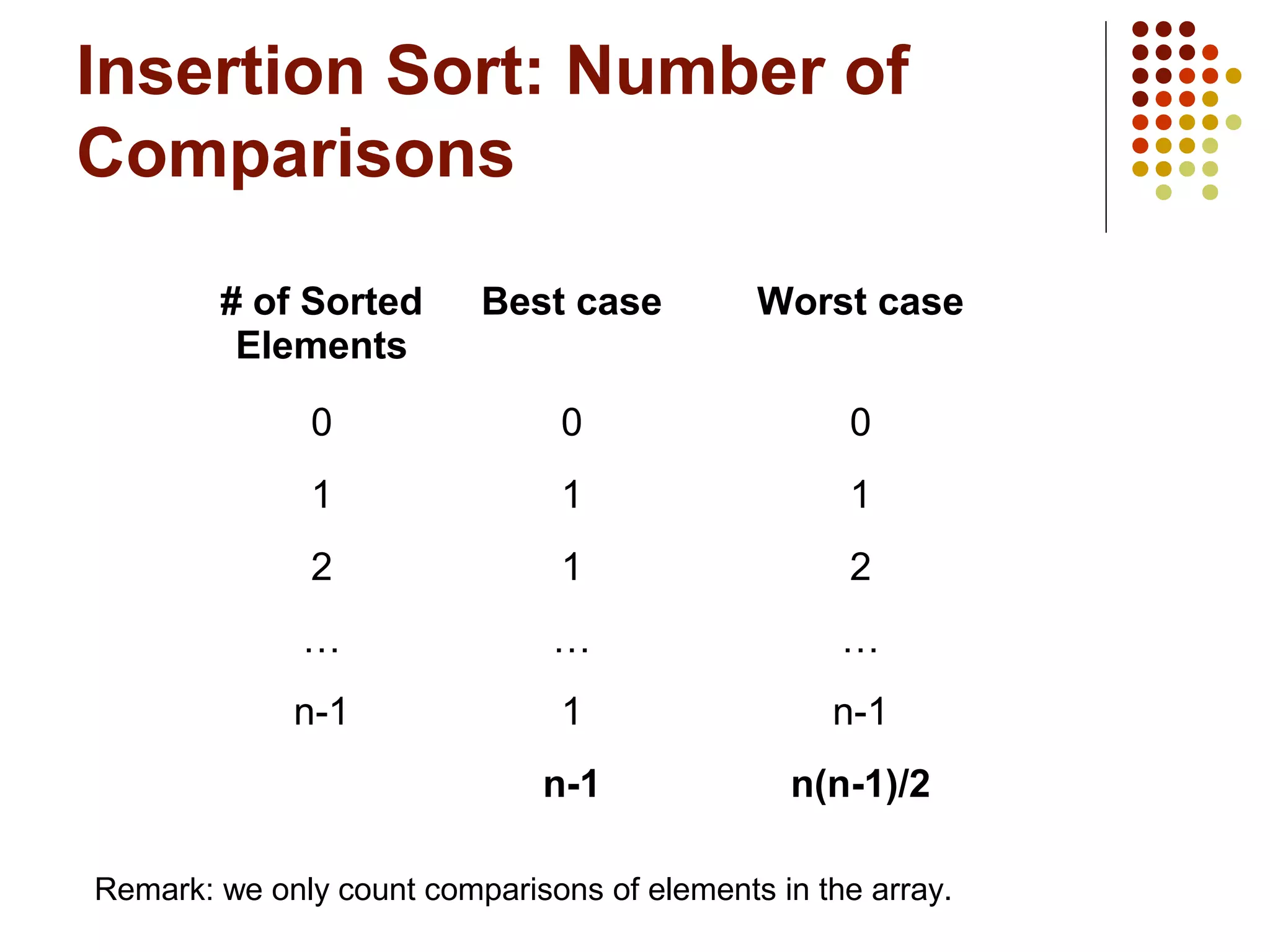
The document discusses algorithm analysis, specifically focusing on insertion sort and bubble sort. It provides details on how each sorting algorithm functions, their code implementations, and their performance analysis in best, worst, and average cases using big O notation. Additionally, it explains how to evaluate the growth rate of algorithms to compare their efficiencies.



![Insertion Sort Algorithm
public void insertionSort(Comparable[] arr) {
for (int i = 1; i < arr.length; ++i) {
Comparable temp = arr[i];
int pos = i;
// Shuffle up all sorted items > arr[i]
while (pos > 0 &&
arr[pos-1].compareTo(temp) > 0) {
arr[pos] = arr[pos–1];
pos--;
} // end while
// Insert the current item
arr[pos] = temp;
}
}](https://image.slidesharecdn.com/lecture-2-150403002246-conversion-gate01/75/Insersion-Bubble-Sort-in-Algoritm-6-2048.jpg)
![public void insertionSort(Comparable[] arr) {
for (int i = 1; i < arr.length; ++i) {
Comparable temp = arr[i];
int pos = i;
// Shuffle up all sorted items > arr[i]
while (pos > 0 &&
arr[pos-1].compareTo(temp) > 0) {
arr[pos] = arr[pos–1];
pos--;
} // end while
// Insert the current item
arr[pos] = temp;
}
}
Insertion Sort Analysis
outer loop
outer times
inner loop
inner times](https://image.slidesharecdn.com/lecture-2-150403002246-conversion-gate01/75/Insersion-Bubble-Sort-in-Algoritm-7-2048.jpg)


![Bubble Sort
public void bubbleSort (Comparable[] arr) {
boolean isSorted = false;
while (!isSorted) {
isSorted = true;
for (i = 0; i<arr.length-1; i++)
if (arr[i].compareTo(arr[i+1]) > 0) {
Comparable tmp = arr[i];
arr[i] = arr[i+1];
arr[i+1] = tmp;
isSorted = false;
}
}
}](https://image.slidesharecdn.com/lecture-2-150403002246-conversion-gate01/75/Insersion-Bubble-Sort-in-Algoritm-11-2048.jpg)