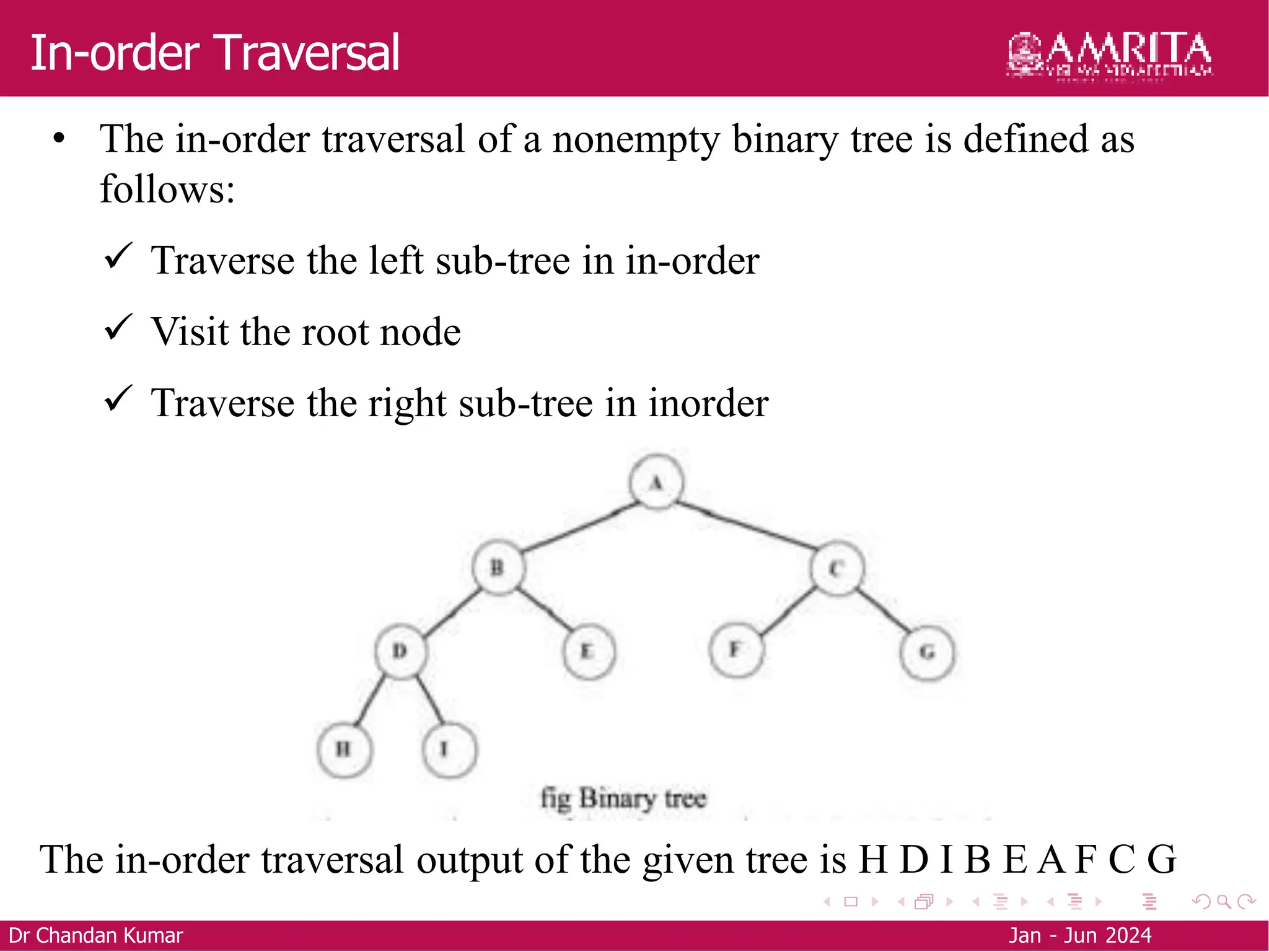
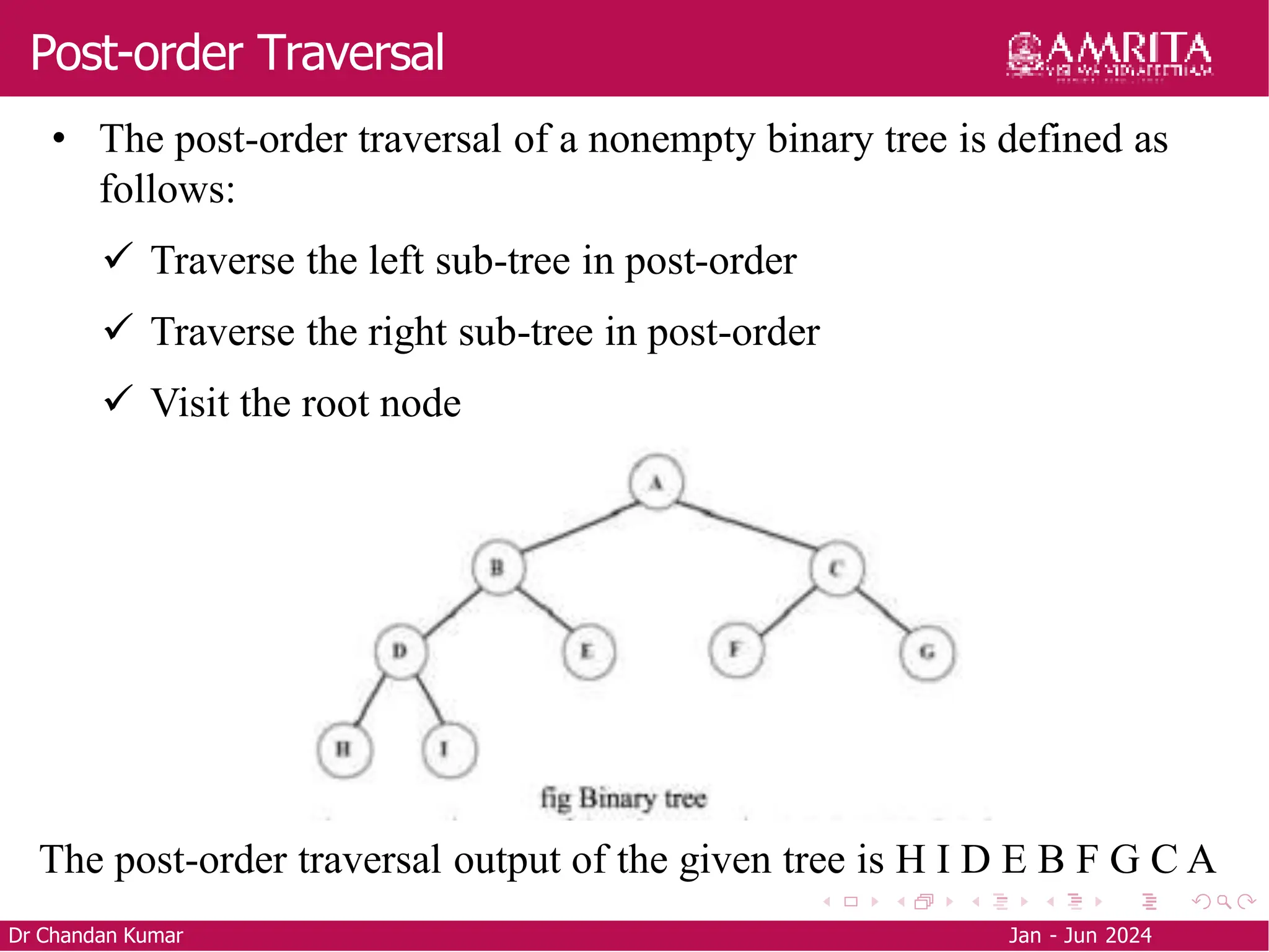
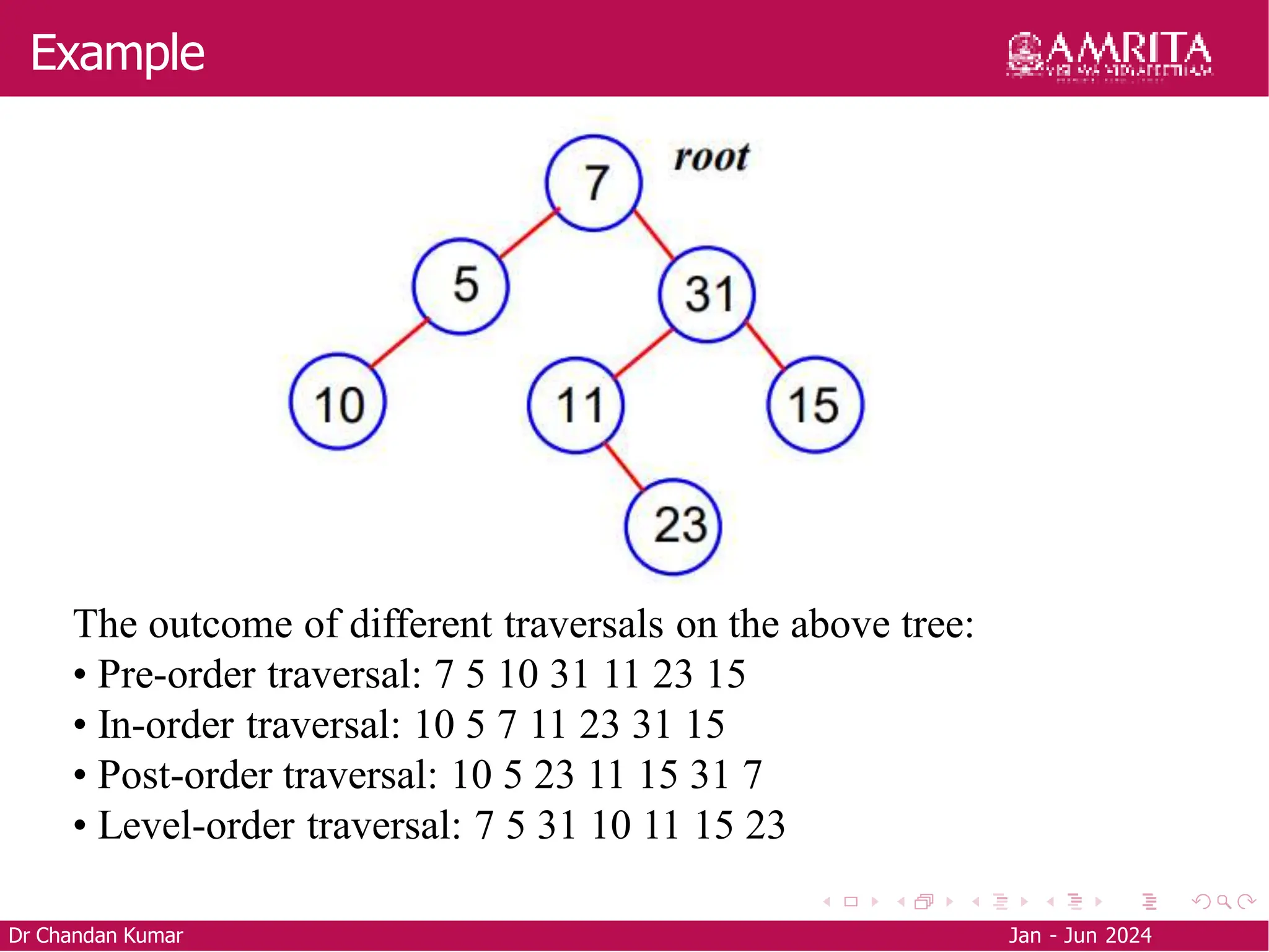
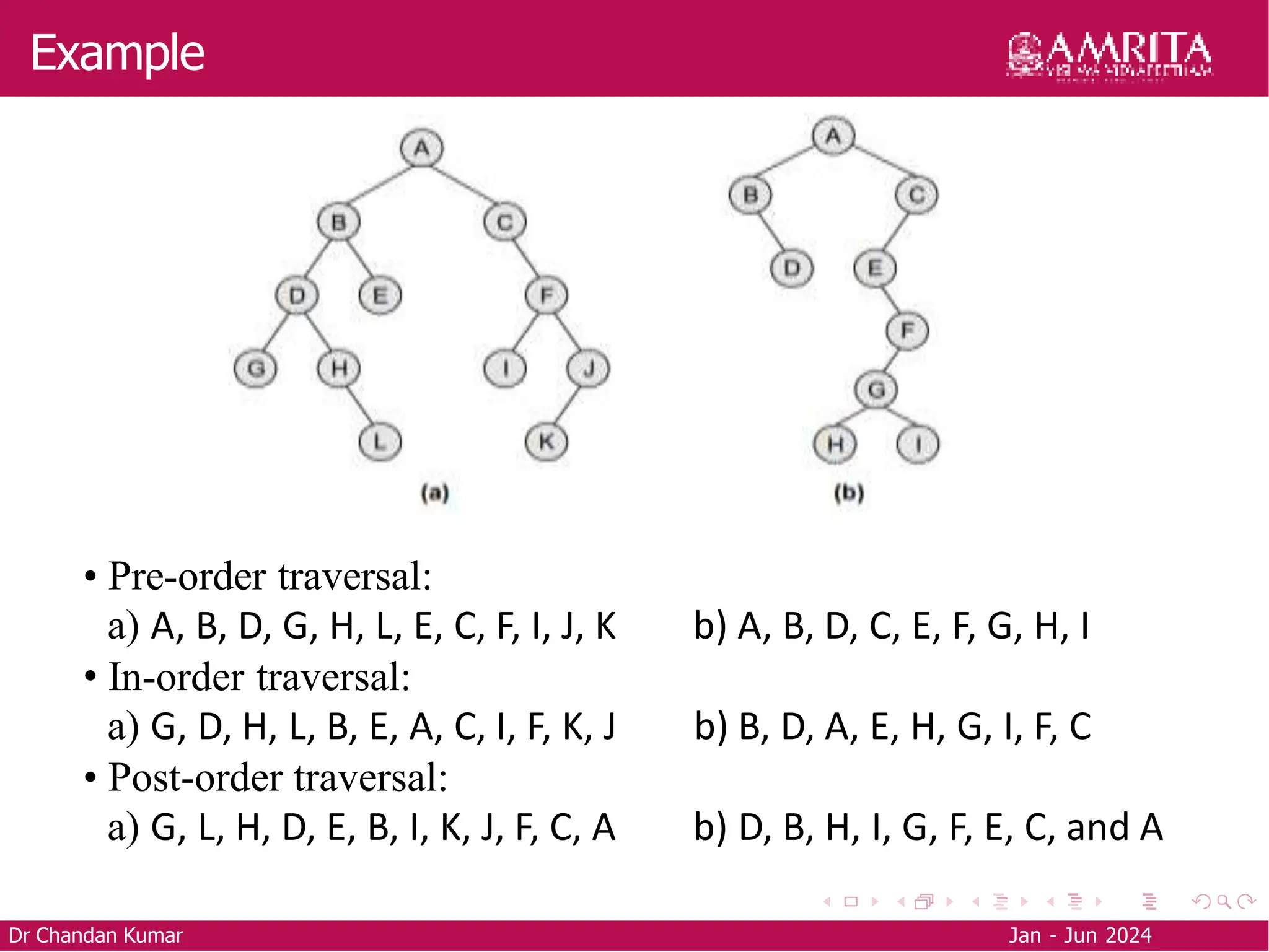
The document is an educational resource on trees and binary trees, detailing definitions, terminology, types of binary trees, and tree traversal methods. It explains the structure of binary trees, including types such as full, degenerate, and complete binary trees, as well as traversal techniques like pre-order, in-order, and post-order. Additionally, it covers how to construct a binary tree from traversal results using in-order and either pre-order or post-order sequences.




















![Constructing a Binary Tree from Traversal Results
Dr Chandan Kumar Jan - Jun 2024
Example:
Input: inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]](https://image.slidesharecdn.com/treesbinarytrees-240625142818-7a651411/75/Introduction-and-basic-of-Trees-and-Binary-Trees-30-2048.jpg)
![Constructing a Binary Tree from Traversal Results
Dr Chandan Kumar Jan - Jun 2024
Example:
Inorder:[ 40, 20 , 50, 10, 60, 30], Postorder: [40, 50, 20, 60, 30, 10]](https://image.slidesharecdn.com/treesbinarytrees-240625142818-7a651411/75/Introduction-and-basic-of-Trees-and-Binary-Trees-31-2048.jpg)
