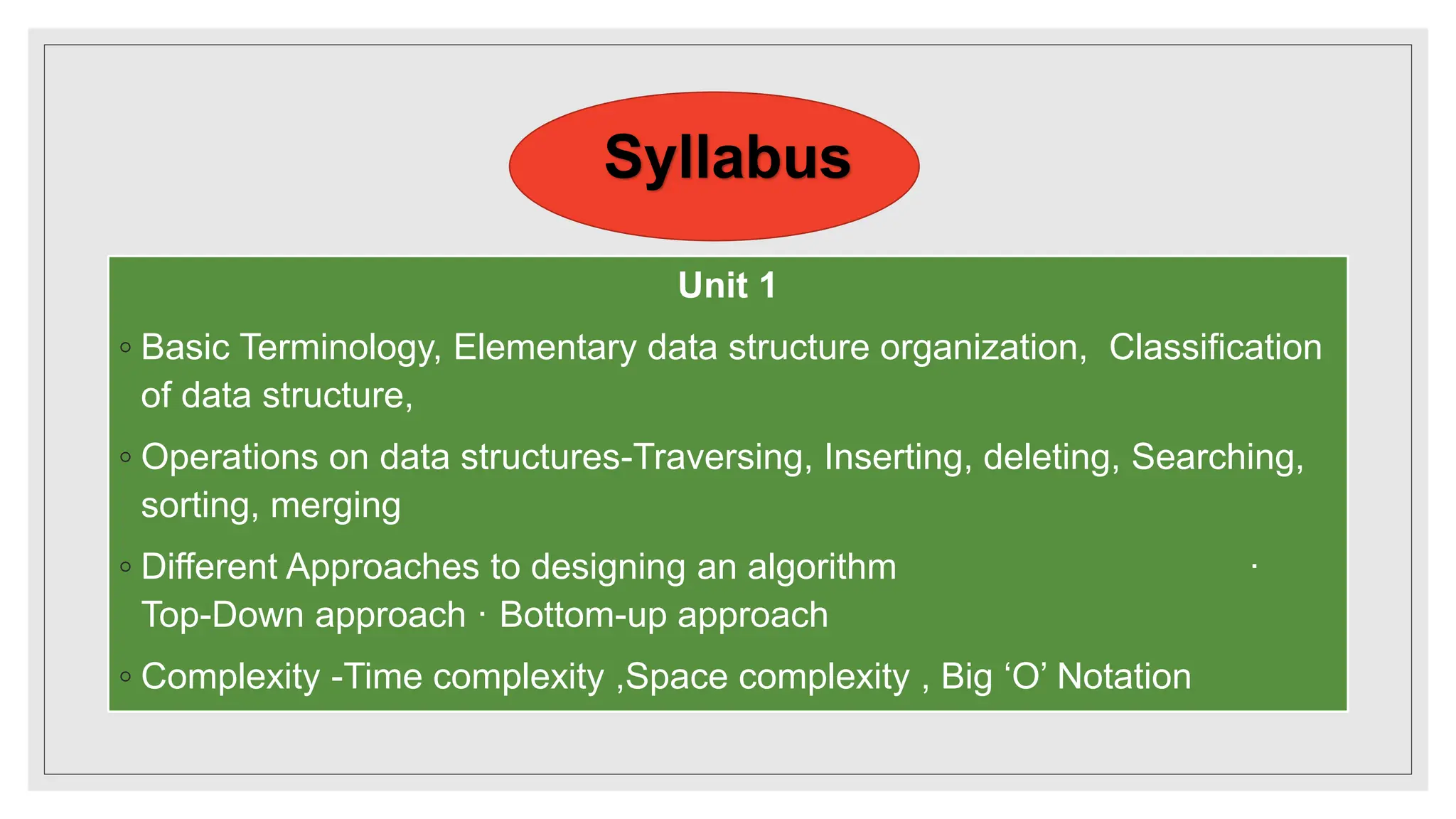
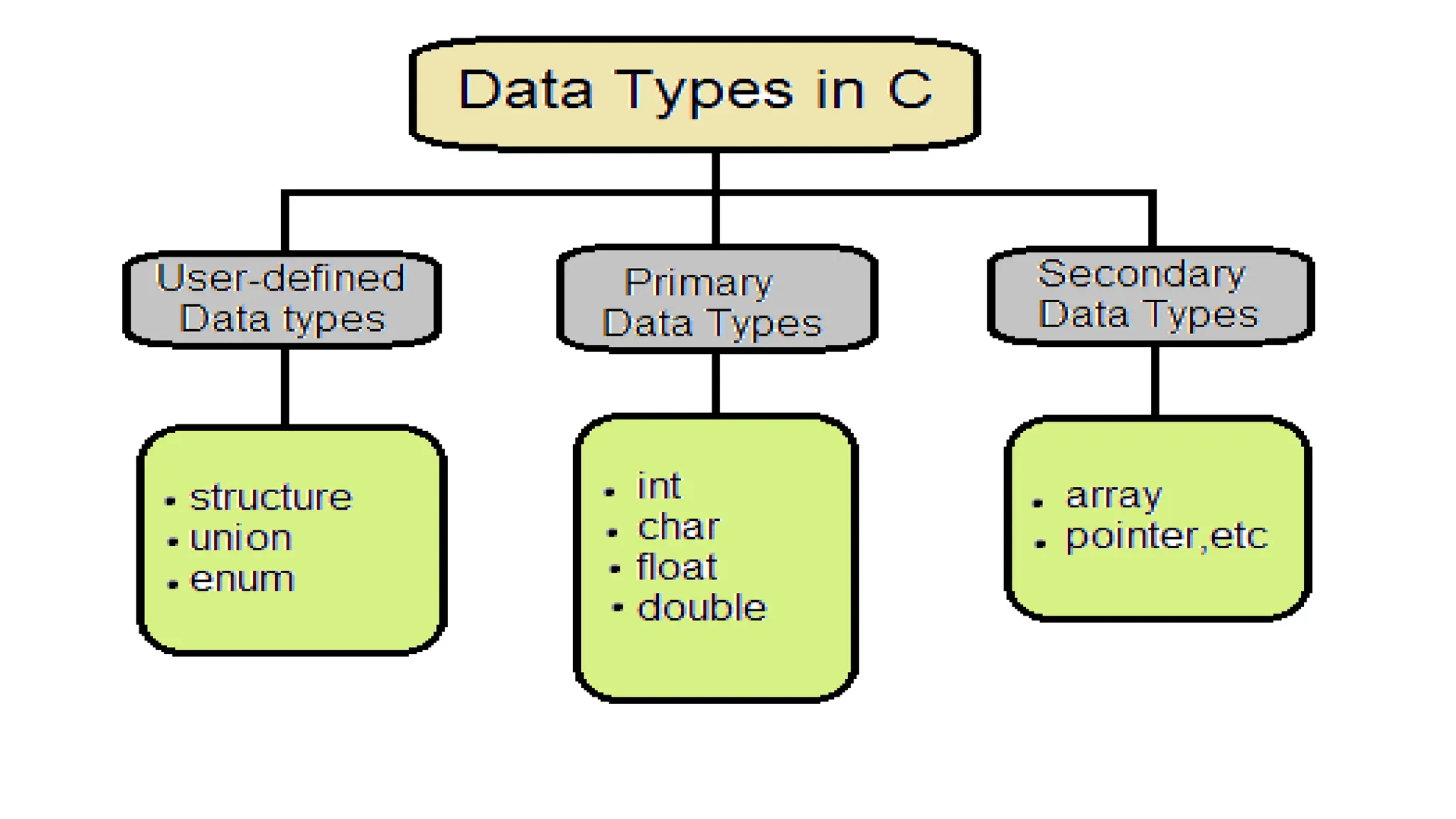
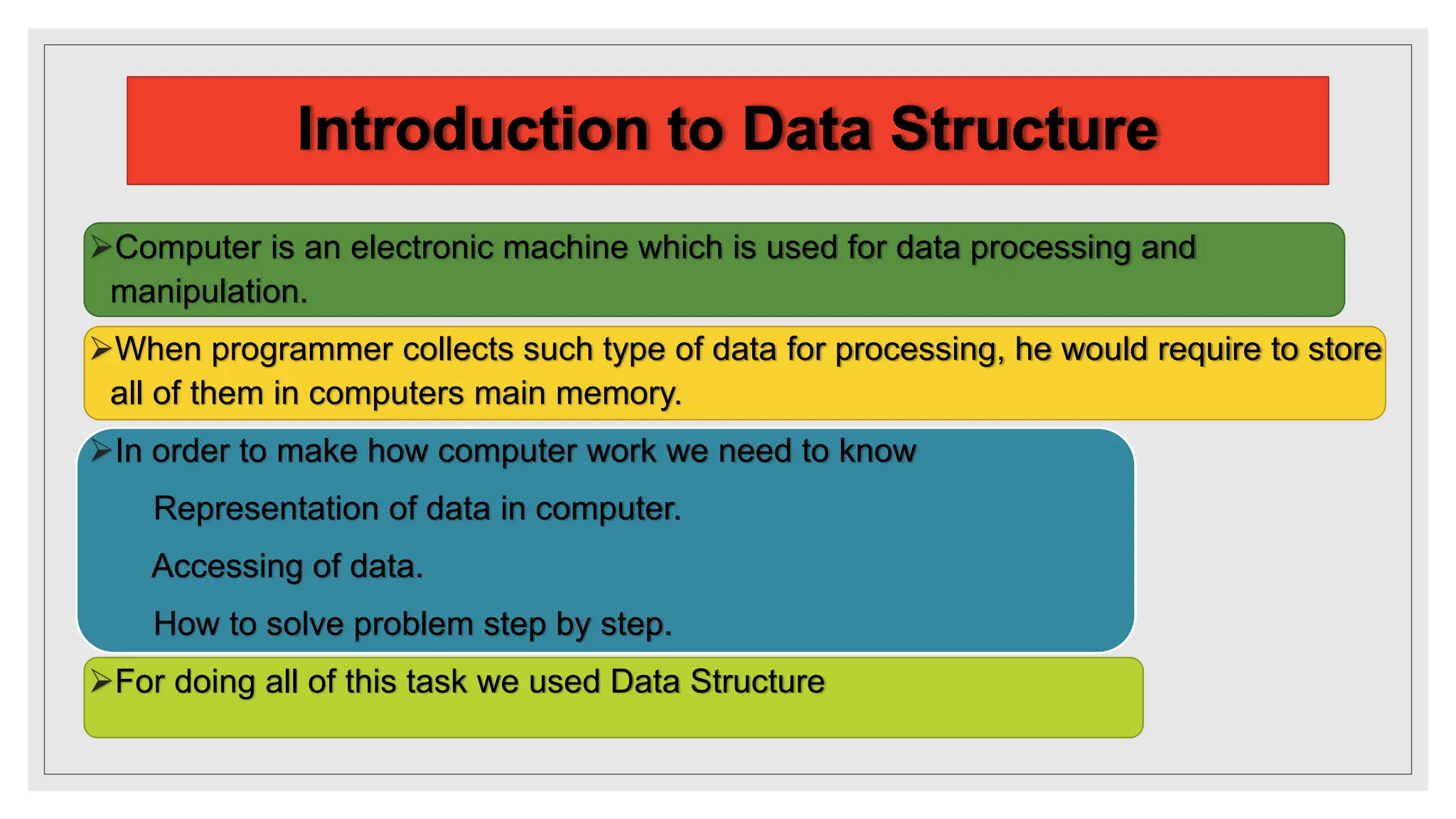
The document outlines the fundamental concepts of data structures and algorithms, including basic terminology, types of data structures (primitive and non-primitive), and the essential operations performed on them. It elaborates on various algorithm design approaches such as top-down and bottom-up, along with complexity analysis including time and space complexity. Additionally, it provides examples of linear and non-linear data structures and highlights the importance of efficient data organization in computer programming.













![Array
◦ Arrays are defined as the collection of similar type of data items stored at contiguous memory
locations.
◦ Arrays are the derived data type in C programming language which can store the primitive type
of data such as int, char, double, float, etc.
◦ Array is the simplest data structure where each data element can be randomly accessed by
using its index number.
◦ For example, if we want to store the marks of a student in 6 subjects, then we don't need to
define different variable for the marks in different subject. instead of that, we can define an array
which can store the marks in each subject at a the contiguous memory locations.
The array marks[10] defines the marks of the student in 10 different subjects where each subject
marks are located at a particular subscript in the array i.e. marks[0] denotes the marks in first
subject, marks[1] denotes the marks in 2nd subject and so on.](https://image.slidesharecdn.com/datastructureppt-231107093343-72d480c3/75/Introduction-to-Data-Structure-17-2048.jpg)
![//Traversing of 1D Array
int main()
{
int a[1000],i,n;
printf("Enter size of array: ");
scanf("%d",&n);
printf("Enter %d elements in the array : ", n);
for(i=0;i<n;i++)
{
scanf("%d", &a[i]);
}
printf("nElements in array are: ");
for(i=0;i<n;i++)
{
printf("%d ", a[i]);
}
return 0;
}](https://image.slidesharecdn.com/datastructureppt-231107093343-72d480c3/75/Introduction-to-Data-Structure-18-2048.jpg)
![2D array
◦ 2D array can be defined as an array of arrays. The 2D array is organized as matrices
which can be represented as the collection of rows and columns.
◦ syntax of declaring two dimensional array
int arr[max_rows][max_columns];
Initializing 2D Arrays
int arr[2][2] = {0,1,2,3}; 0 1
2 3
arr[0][0]=0
arr[0][1]=1
arr[1][0]=2
arr[1][1]=3](https://image.slidesharecdn.com/datastructureppt-231107093343-72d480c3/75/Introduction-to-Data-Structure-19-2048.jpg)
![//Traversing od 2D array
#include <stdio.h>
void main ()
{
int arr[3][3],i,j;
for (i=0;i<3;i++)
{
for (j=0;j<3;j++)
{
printf("Enter a[%d][%d]: ",i,j);
scanf("%d",&arr[i][j]);
}
}
printf("n printing the elements ....n");
for(i=0;i<3;i++)
{
printf("n");
for (j=0;j<3;j++)
{
printf("%dt",arr[i][j]);
} } }](https://image.slidesharecdn.com/datastructureppt-231107093343-72d480c3/75/Introduction-to-Data-Structure-20-2048.jpg)
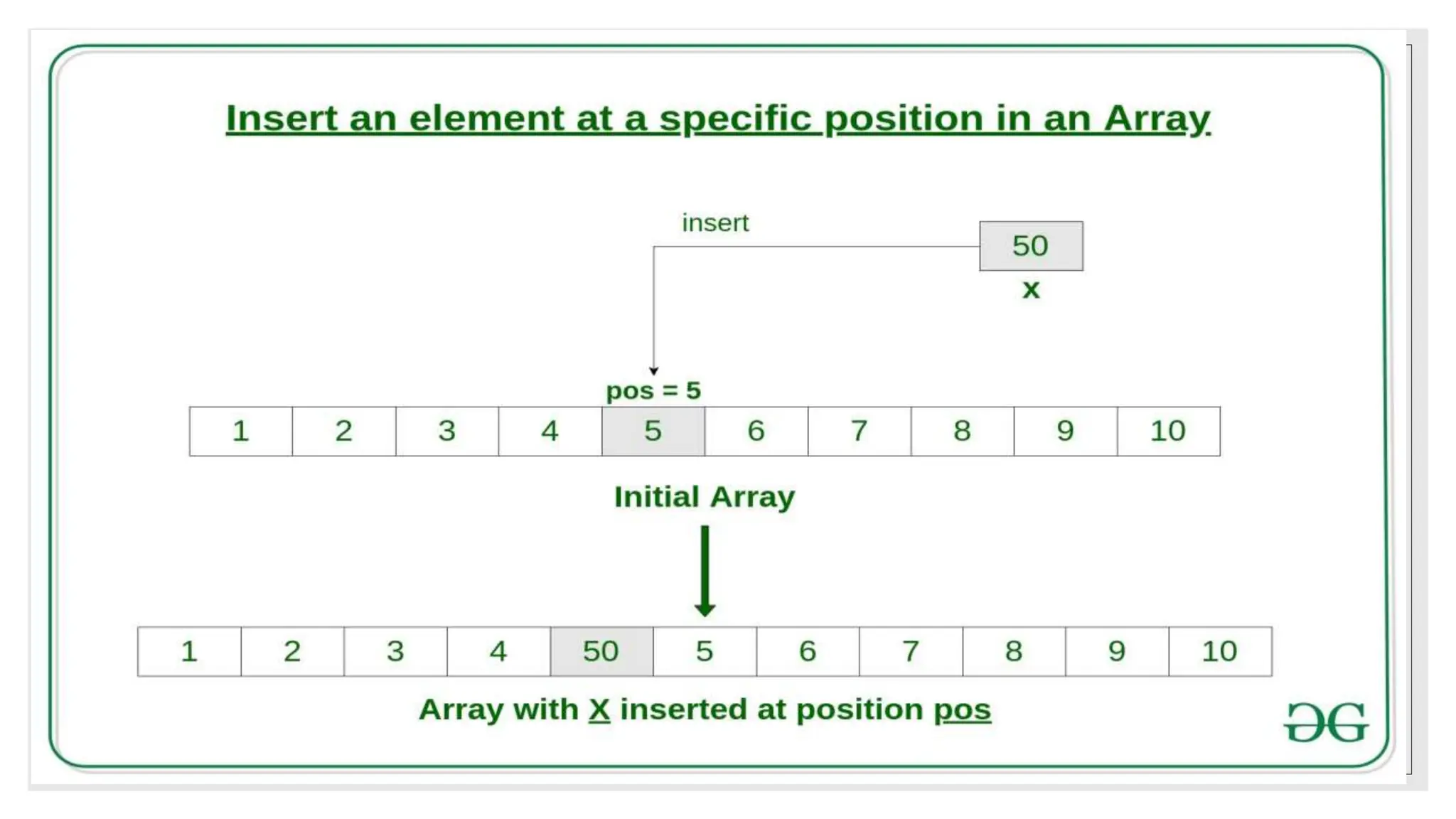
![#include <stdio.h>
#include<conio.h>
void main()
{
int array[50], position, i, n, value;
clrscr();
printf("Enter number of elements in the arrayn");
scanf("%d", &n);
printf("Enter %d elementsn", n);
for (i = 0; i < n; i++)
{
scanf("%d", &array[i]);
}
printf("Please enter the location where you want to insert an new elementn");
scanf("%d", &position);](https://image.slidesharecdn.com/datastructureppt-231107093343-72d480c3/75/Introduction-to-Data-Structure-22-2048.jpg)
![printf("Please enter the valuen");
scanf("%d", &value);
for (i = n - 1; i >= position - 1; i--)
{
array[i+1] = array[i];
}
array[position-1] = value;
printf("Resultant array isn");
for (i = 0; i <= n; i++)
{
printf("%dn", array[i]);
}
getch();
}](https://image.slidesharecdn.com/datastructureppt-231107093343-72d480c3/75/Introduction-to-Data-Structure-23-2048.jpg)

![#include <stdio.h>
#include <conio.h>
int main()
{
int array[100], position, i, n;
clrscr();
printf("Enter number of elements in arrayn");
scanf("%d", &n);
printf("Enter %d elementsn", n);
for ( i = 0 ; i < n ; i++ )
{
scanf("%d", &array[i]);
}
printf("Enter the location where you wish to delete elementn");
scanf("%d", &position);](https://image.slidesharecdn.com/datastructureppt-231107093343-72d480c3/75/Introduction-to-Data-Structure-25-2048.jpg)
![if ( position >= n+1 )
{
printf("Deletion not possible.n");
}
else
{
for ( i = position - 1 ; i < n - 1 ; i++ )
array[i] = array[i+1];
printf("Resultant array isn");
for( i = 0 ; i < n - 1 ; i++ )
printf("%dn", array[i]);
}
getch();
}](https://image.slidesharecdn.com/datastructureppt-231107093343-72d480c3/75/Introduction-to-Data-Structure-26-2048.jpg)











