Knapsack Algorithm www.geekssay.com

Knapsack Problem Notes

V.S. Subrahmanian
University of Maryland

© 5/7/2002 V.S. 1

Knapsack Problem
• You have a knapsack that has capacity (weight) C.
• You have several items I1,…,In.
• Each item Ij has a weight wj and a benefit bj.
• You want to place a certain number of copies of
each item Ij in the knapsack so that:
– The knapsack weight capacity is not exceeded and
– The total benefit is maximal.

© 5/7/2002 V.S. 2

Example
Item Weight Benefit

A 2 60

B 3 75

C 4 90

Capacity = 5
© 5/7/2002 V.S. 3

Key question
• Suppose f(w) represents the maximal
possible benefit of a knapsack with weight
w.
• We want to find (in the example) f(5).
• Is there anything we can say about f(w) for
arbitrary w?

© 5/7/2002 V.S. 4

Key observation
• To fill a knapsack with items of weight w, we
must have added items into the knapsack in some
order.
• Suppose the last such item was Ij with weight wi
and benefit bi.
• Consider the knapsack with weight (w- wi).
Clearly, we chose to add Ij to this knapsack
because of all items with weight wi or less, Ij had
the max benefit bi.
© 5/7/2002 V.S. 5

Key observation
• Thus, f(w) = MAX { bj + f(w-wj) | Ij is an
item}.
• This gives rise to an immediate recursive
algorithm to determine how to fill a
knapsack.

© 5/7/2002 V.S. 6

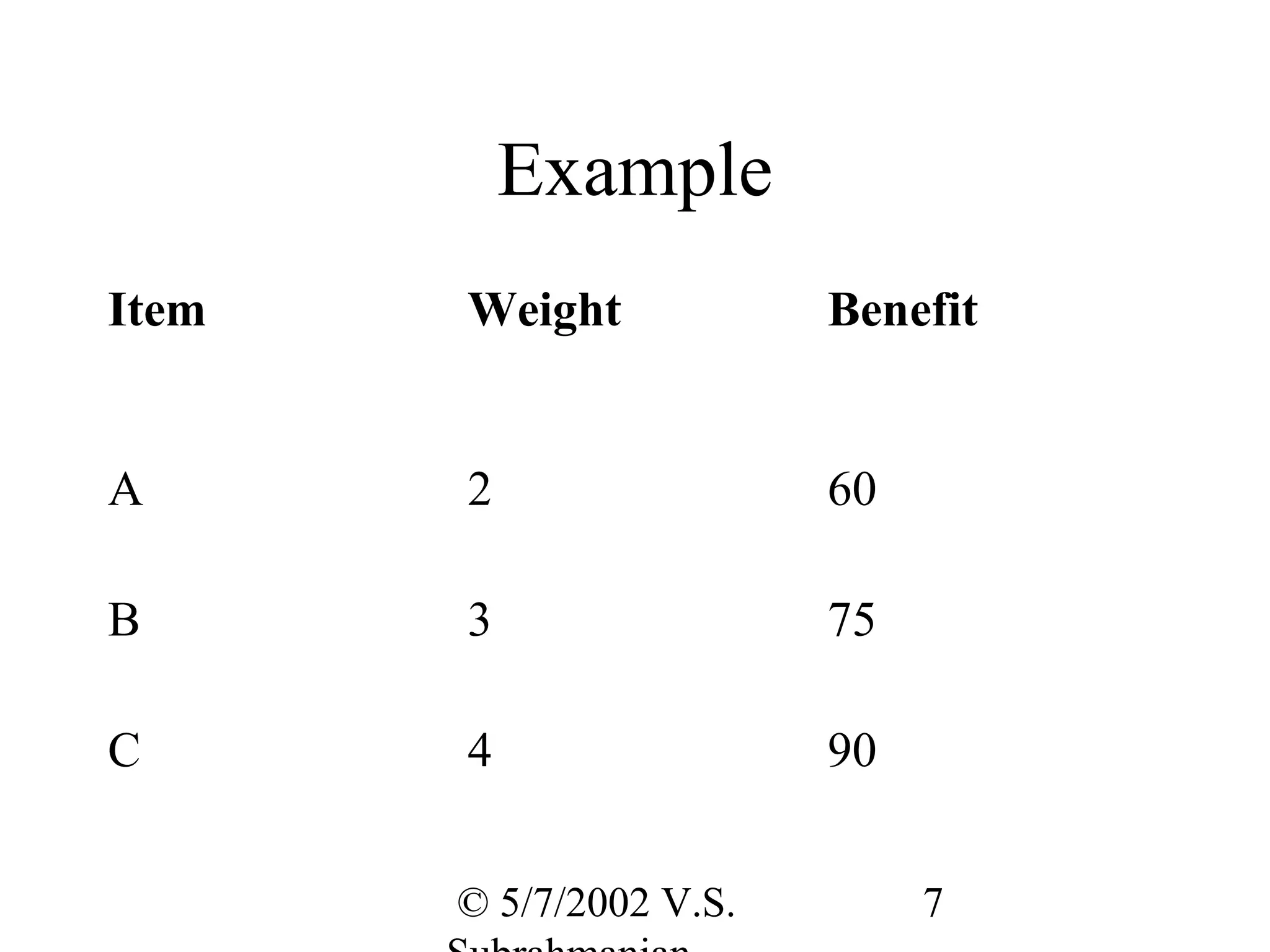
Example
Item Weight Benefit

A 2 60

B 3 75

C 4 90

© 5/7/2002 V.S. 7

f(0), f(1)
• f(0) = 0. Why? The knapsack with capacity
0 can have nothing in it.
• f(1) = 0. There is no item with weight 1.

© 5/7/2002 V.S. 8

f(2)
• f(2) = 60. There is only one item with
weight 60.
• Choose A.

© 5/7/2002 V.S. 9

f(3)
• f(3) = MAX { bj + f(w-wj) | Ij is an item}.
= MAX { 60+f(3-2), 75 + f(3-3)}
= MAX { 60 + 0, 75 + 0 }
= 75.
Choose B.

© 5/7/2002 V.S. 10

f(4)
= MAX { 60 + f(4-2), 75 + f(4-3), 90+f(4-4)}
= MAX { 60 + 60, 75 + f(1), 90 + f(0)}
= MAX { 120, 75, 90}
=120.
Choose A.

© 5/7/2002 V.S. 11

f(5)
= MAX { 60 + f(5-2), 75 + f(5-3), 90+f(5-4)}
= MAX { 60 + f(3), 75 + f(2), 90 + f(1)}
= MAX { 60 + 75, 75 + 60, 90+0}
= 135.
Choose A or B.

© 5/7/2002 V.S. 12

Result
• Optimal knapsack weight is 135.
• Two possible optimal solutions:
– Choose A during computation of f(5). Choose
B in computation of f(3).
– Choose B during computation of f(5). Choose
A in computation of f(2).
• Both solutions coincide. Take A and B.

© 5/7/2002 V.S. 13

Another example
• Knapsack of capacity 50.
• 3 items
– Item 1 has weight 10, benefit 60
– Item 2 has weight 20,benefit 100
– Item 3 has weight 30, benefit 120.

© 5/7/2002 V.S. 14

f(0),..,f(9)
• All have value 0.

© 5/7/2002 V.S. 15

f(10),..,f(19)
• All have value 10.
• Choose Item 1.

© 5/7/2002 V.S. 16

f(30),…,f(39)
• f(30) = MAX { 60 + f(20), 100 + f(10), 120
+ f(0) }
= MAX { 60 + 120, 100+60, 120+0}
= 180
Choose item 1.

© 5/7/2002 V.S. 18

f(40),…,f(49)
• F(40) = MAX { 60 + f(30), 100 + f(20), 120
+ f(10)}
= MAX { 60 + 180, 100+120, 120 + 60}
= 240.
Choose item 1.

© 5/7/2002 V.S. 19

f(50)
• f(50) = MAX { 60 + f(40), 100 + f(30), 120
+ f(20) }
= MAX { 60 + 240, 100+180, 120 + 120}
= 300.
Choose item 1.

© 5/7/2002 V.S. 20

Knapsack Problem Variants
• 0/1 Knapsack problem: Similar to the
knapsack problem except that for each item,
only 1 copy is available (not an unlimited
number as we have been assuming so far).
• Fractional knapsack problem: You can take
a fractional number of items. Has the same
constraint as 0/1 knapsack. Can solve using
a greedy algorithm.
© 5/7/2002 V.S. 21

0/1 Knapsack
• f[j,w] = best solution having weight exactly
w after considering j elements
• If j >= C: f[j,w] = f[j-1,w]
• Otherwise: f[j,w] =
Best solution after adding k-1 items
• MAXremaining items {
– f[j-1,w], Replace an item with the k’th item

– f[j-1,w-wj]+bj }

© 5/7/2002 V.S. 22

0/1 Knapsack Algorithm
For w = 0 to C do f[w]=0; (* initialize *)
For j=1 to n do
for w=C downto wj do
if f[w-wj] + bj > f[w] then
f[w] = f[w-wj] + bj

O(n.C) algorithm
© 5/7/2002 V.S. 23

Fractional knapsack
• Much easier
• For item Ij, let rj = bj/wj. This gives you the
benefit per measure of weight.
• Sort the items in descending order of rj
• Pack the knapsack by putting as many of
each item as you can walking down the
sorted list.
© 5/7/2002 V.S. 24

Knapsack Algorithm www.geekssay.com

More Related Content

What's hot

Similar to Knapsack Algorithm www.geekssay.com

More from Hemant Gautam

Knapsack Algorithm www.geekssay.com