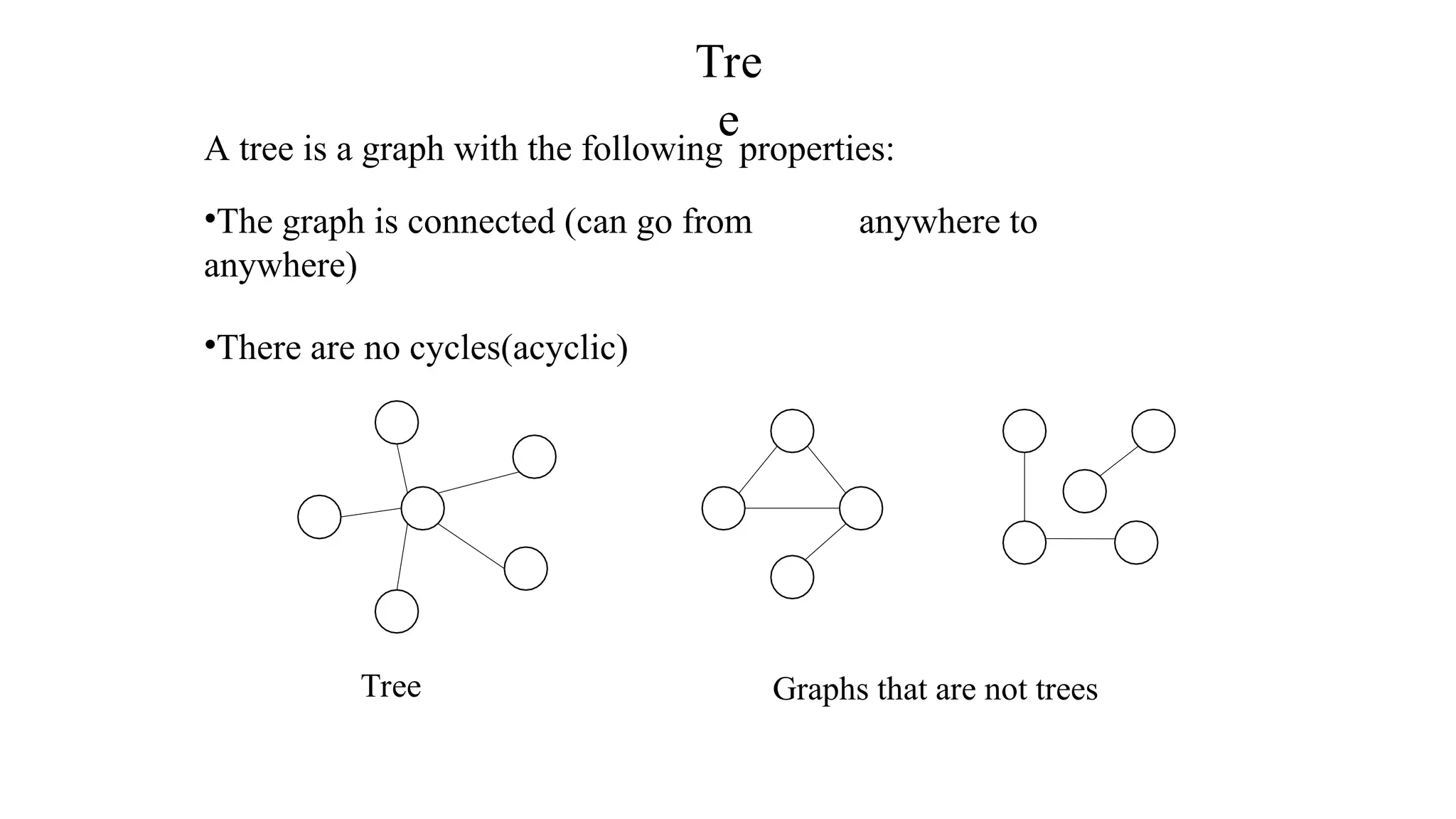
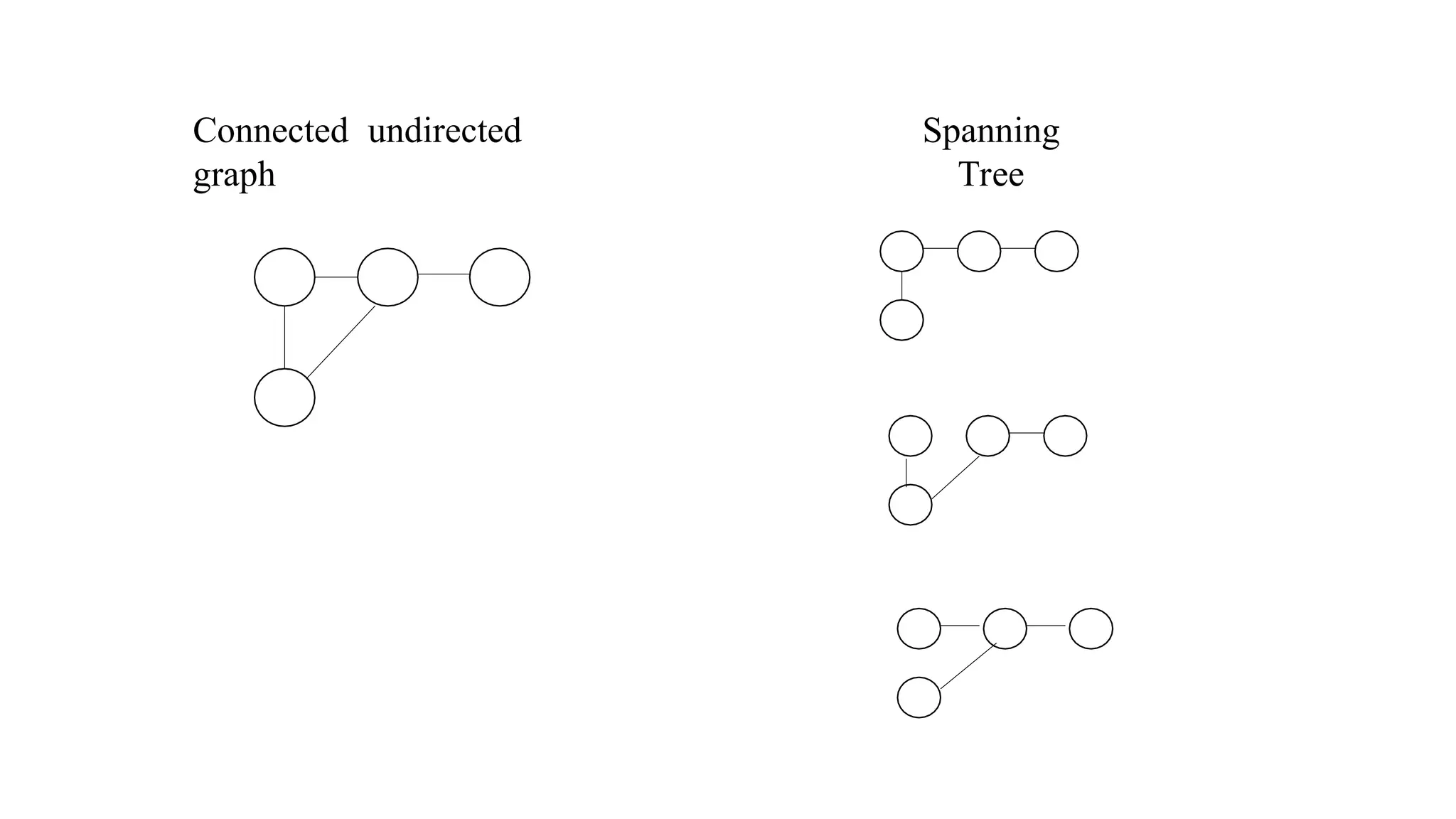
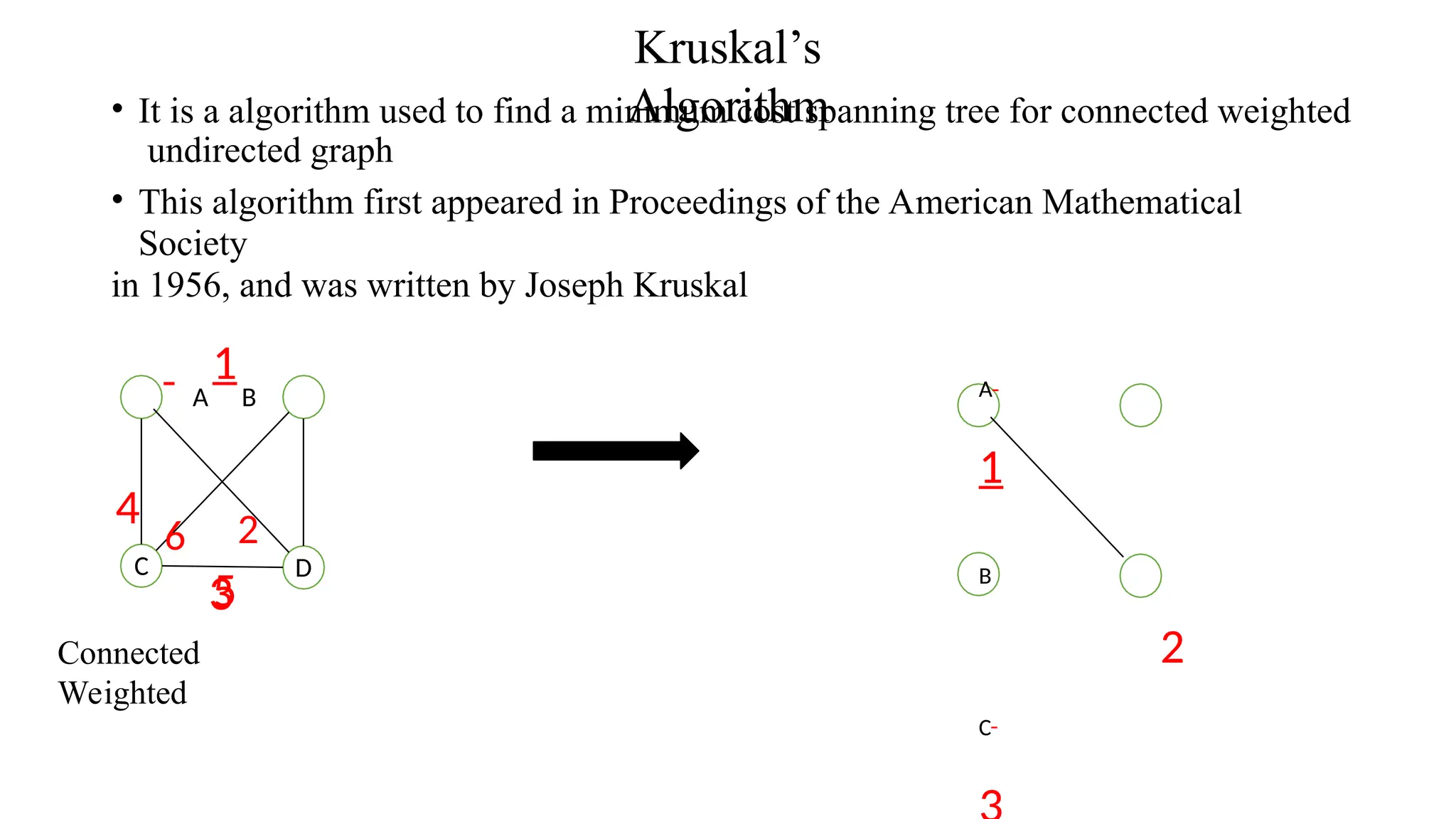
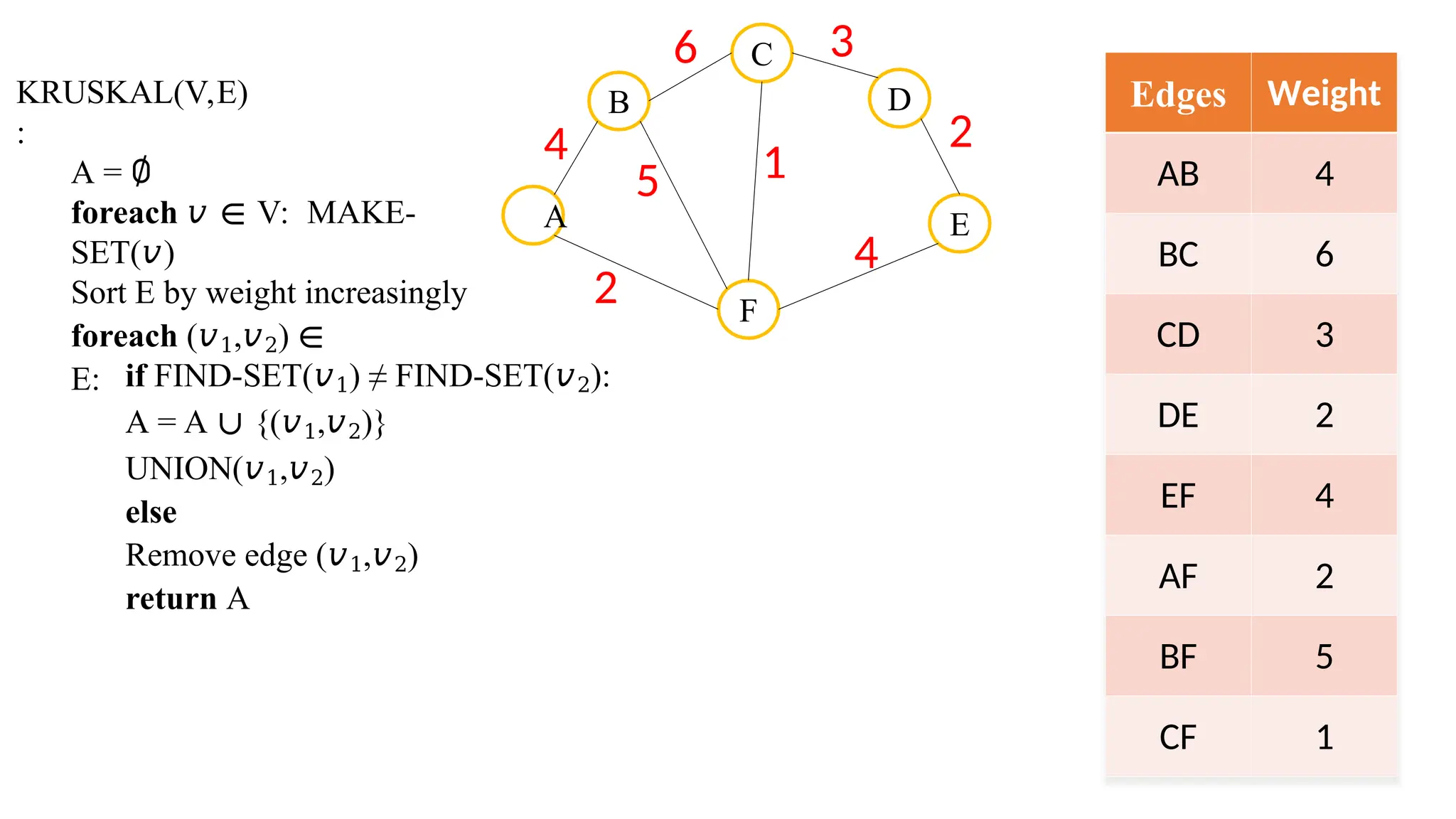
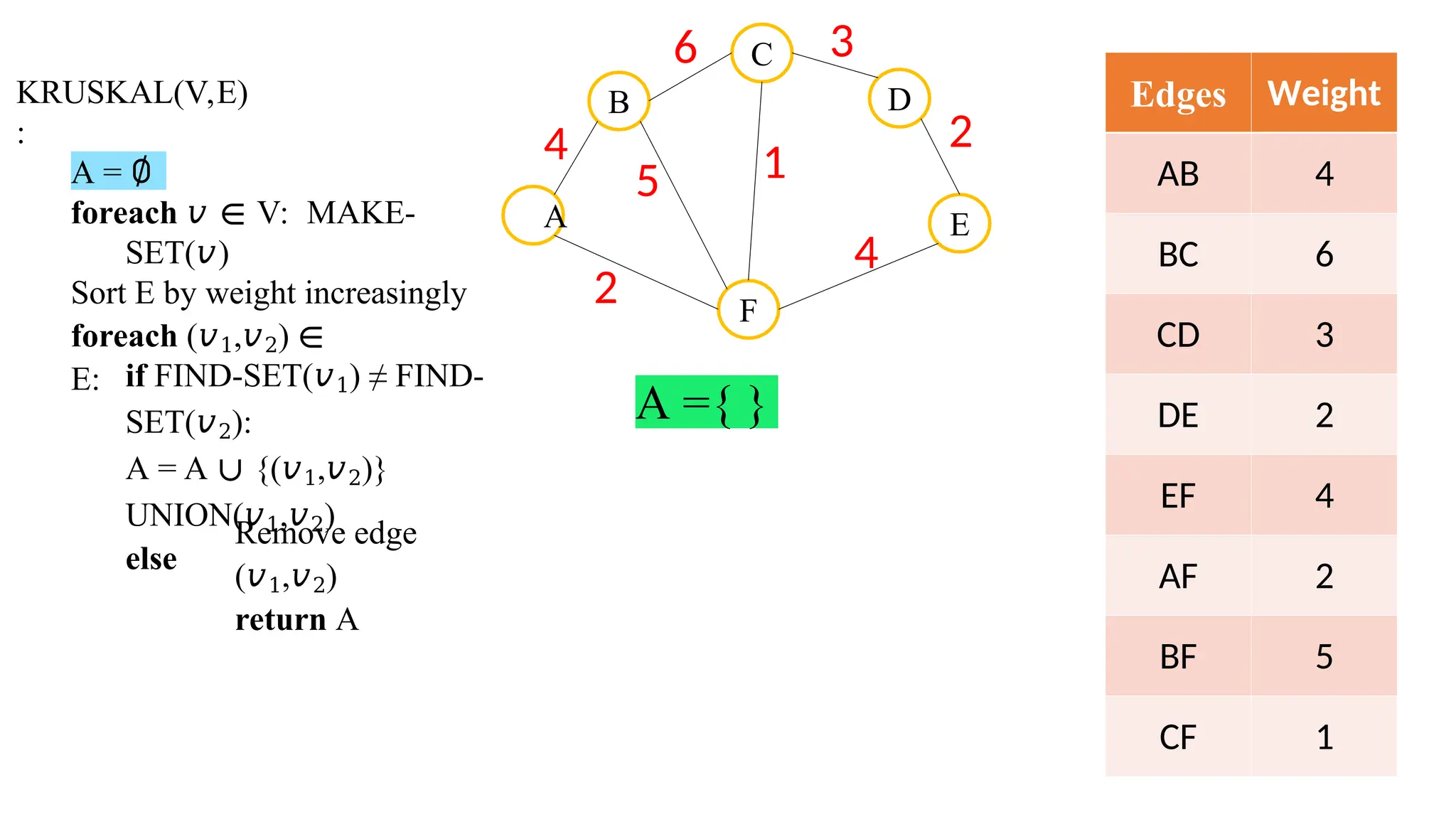
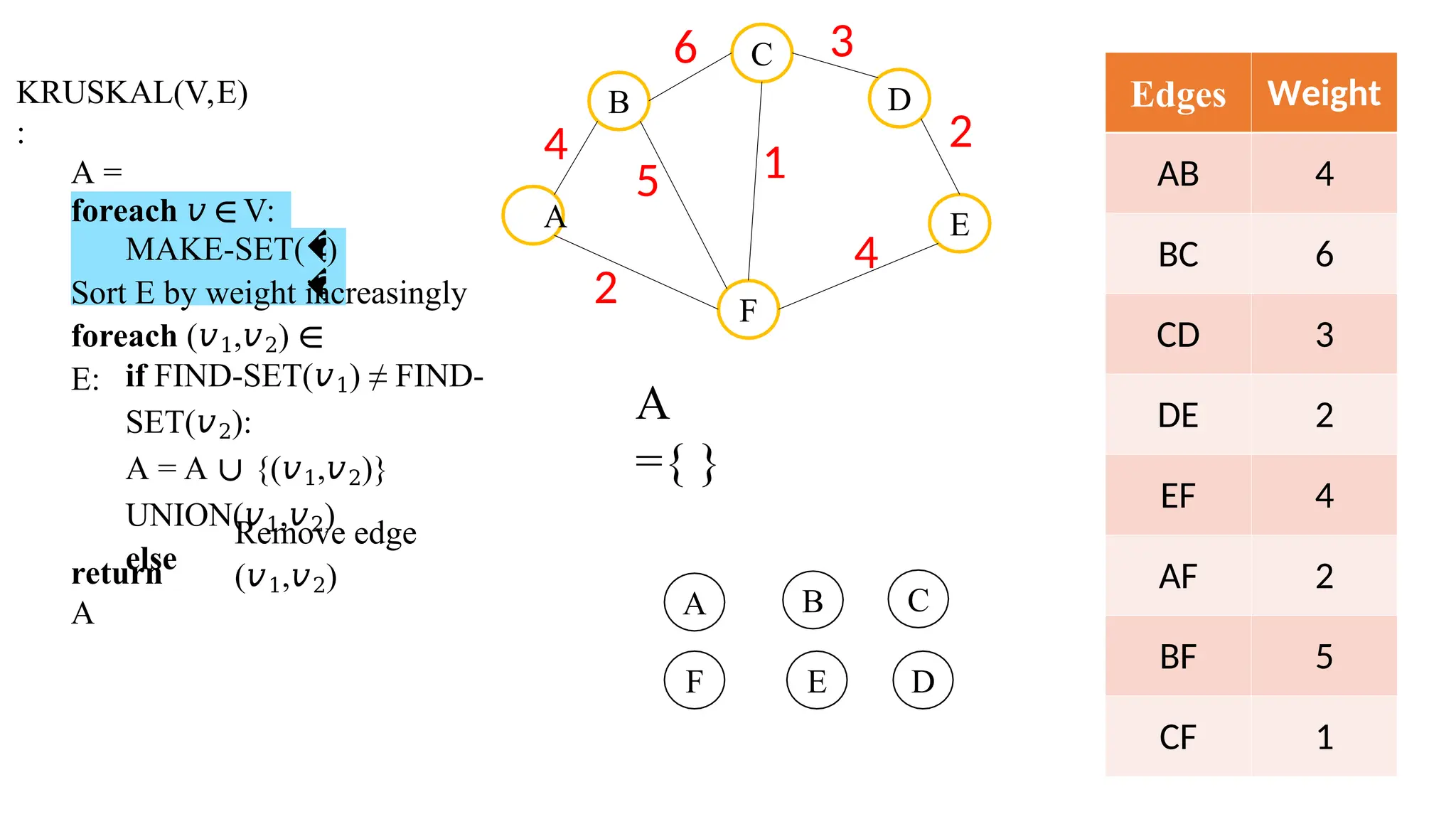
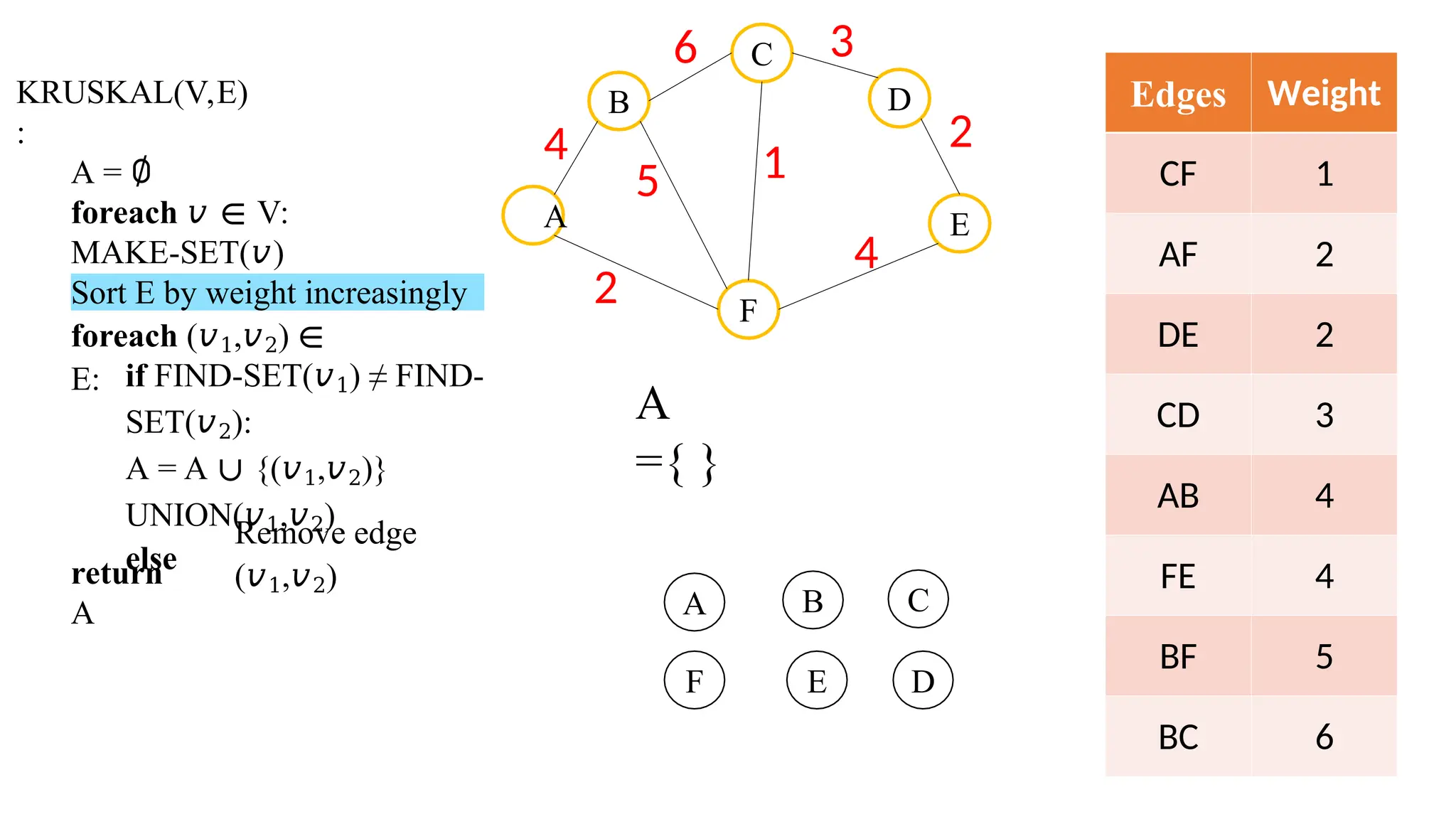
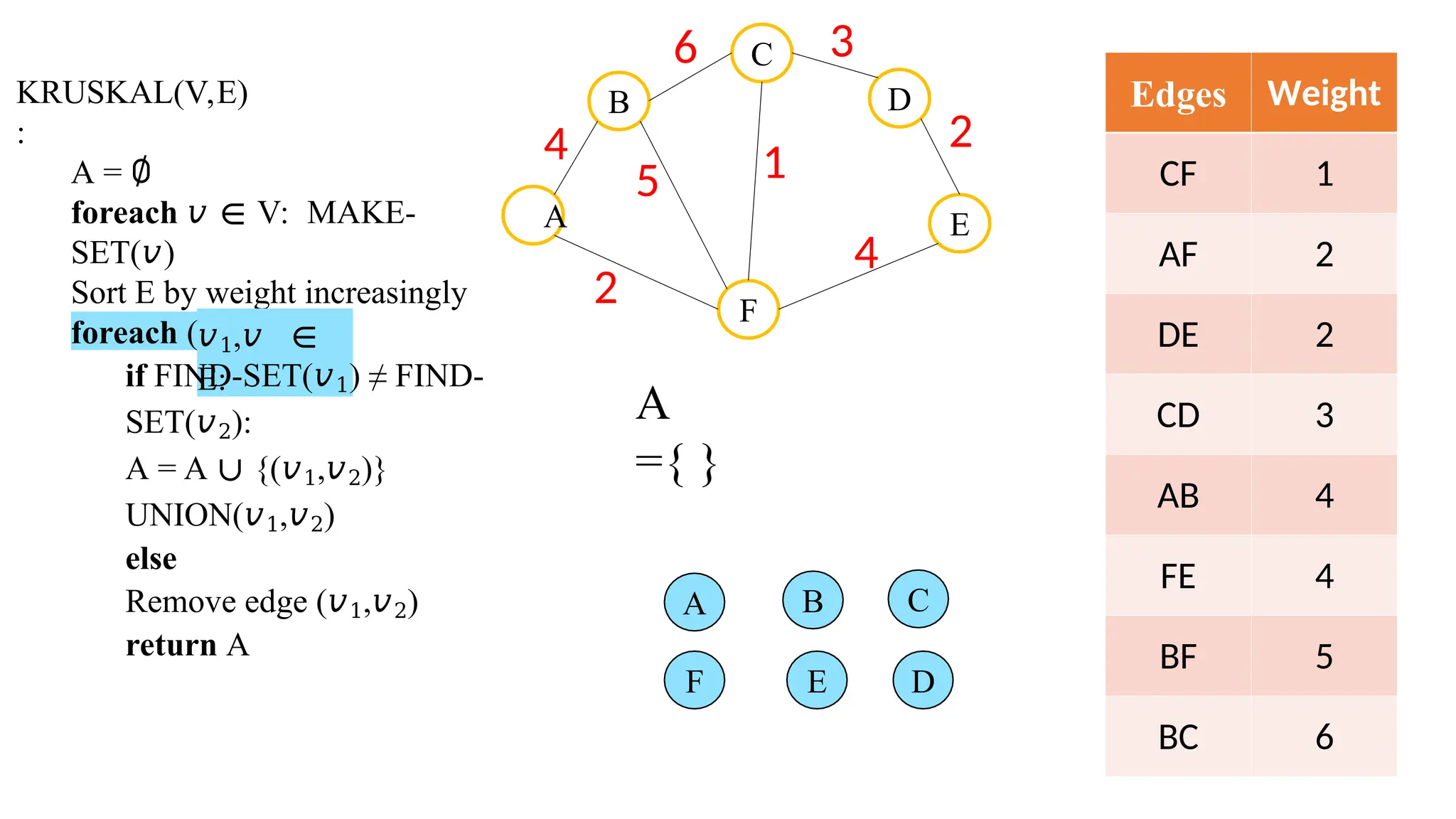
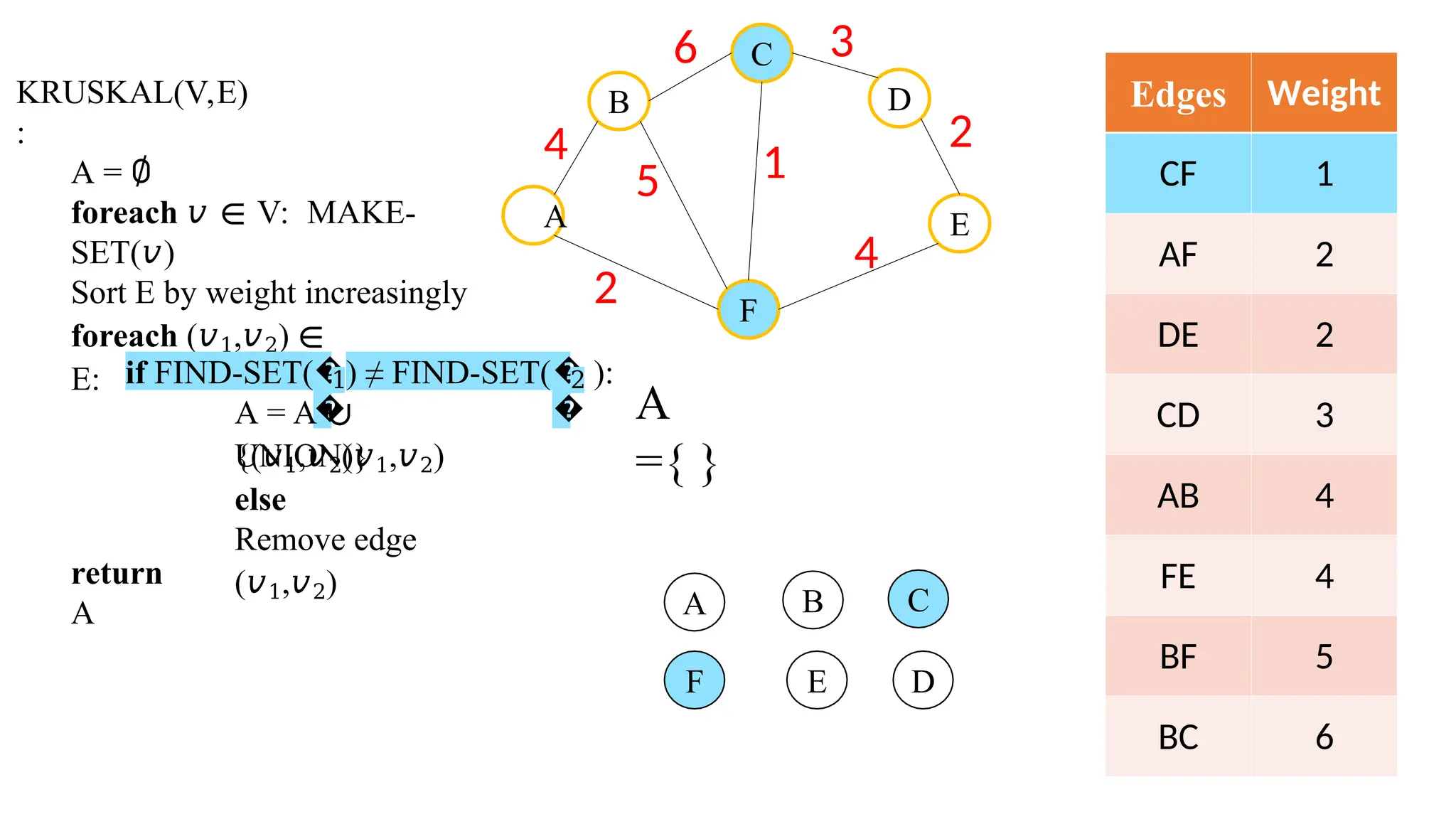
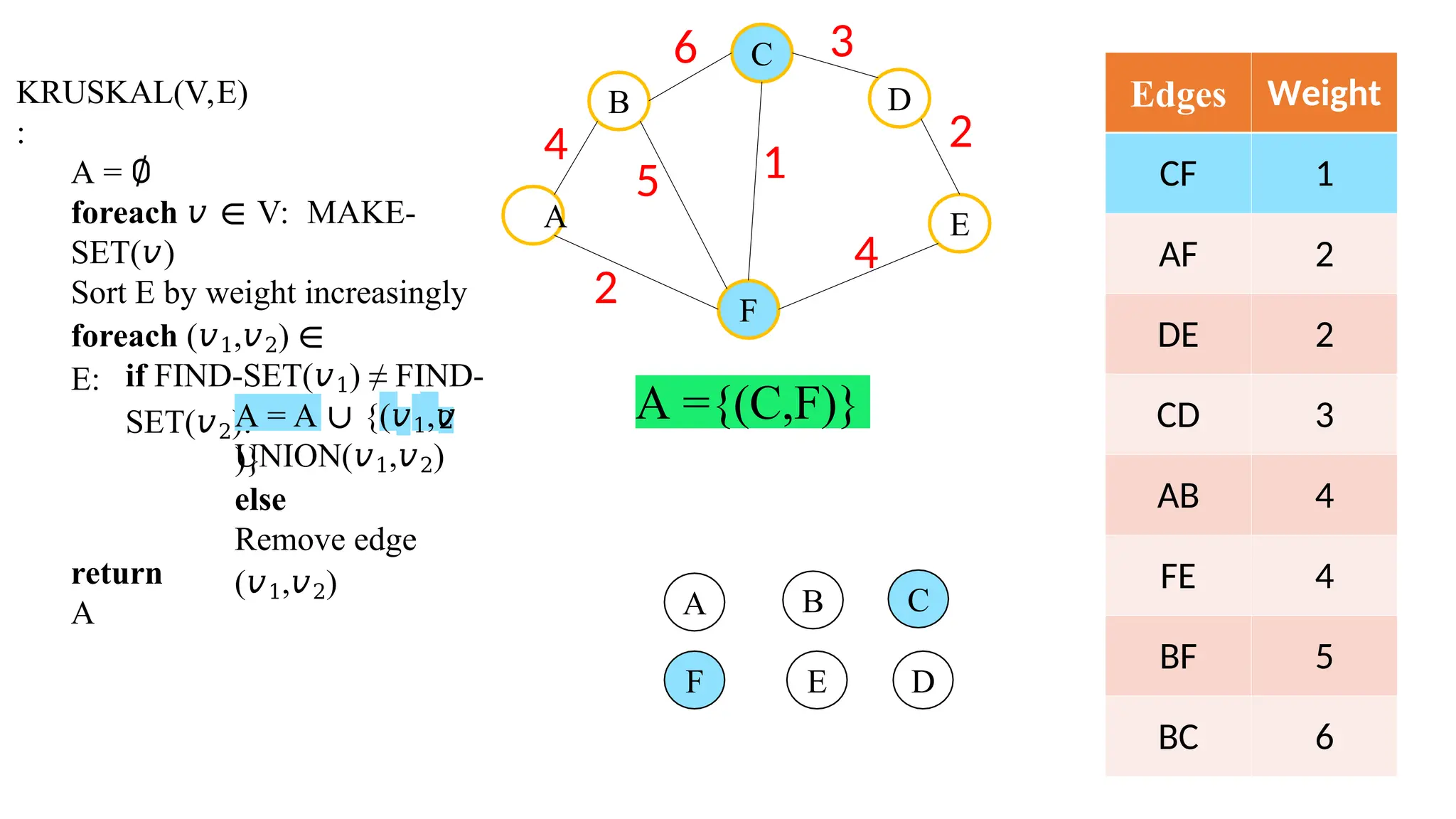
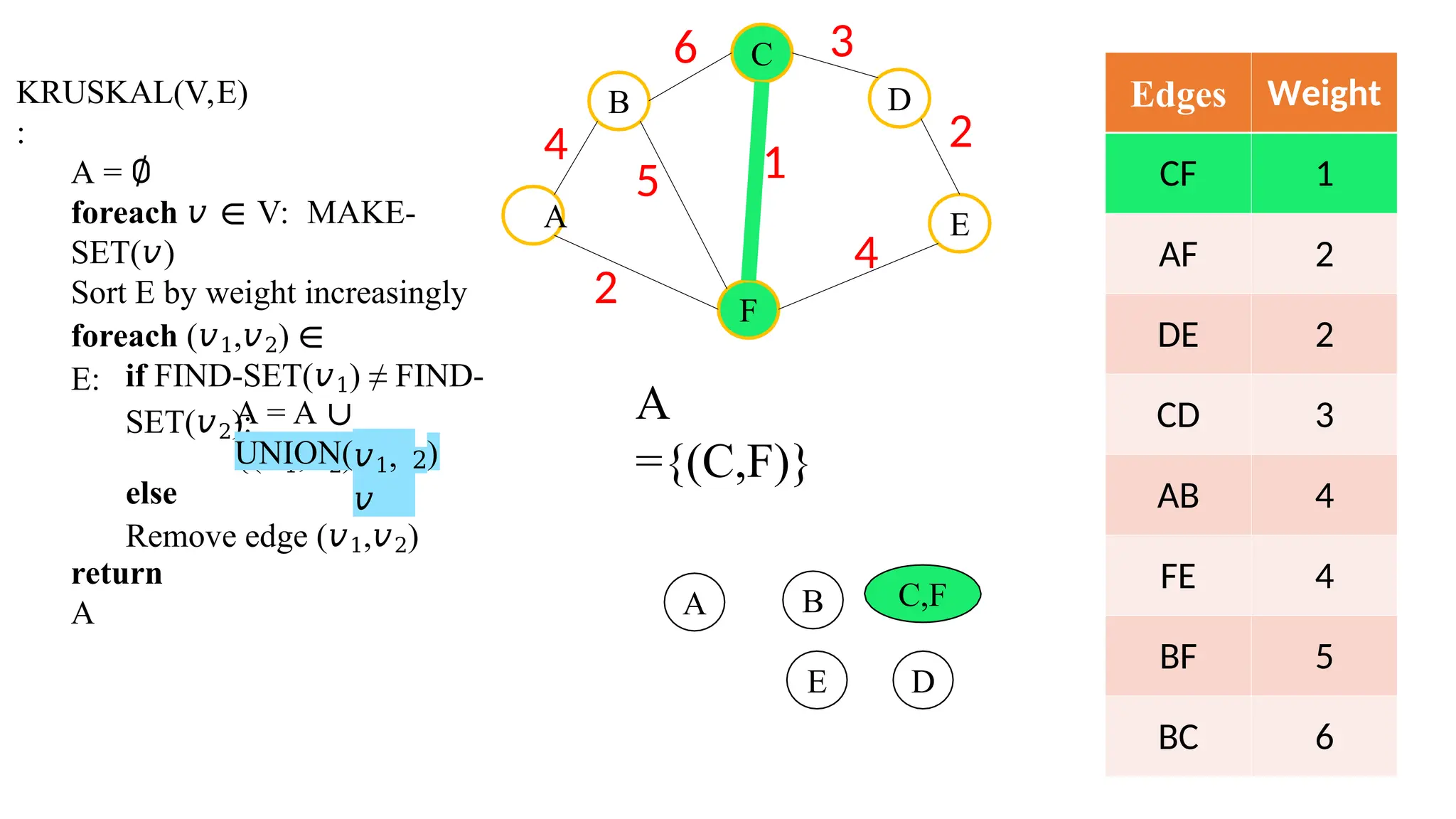
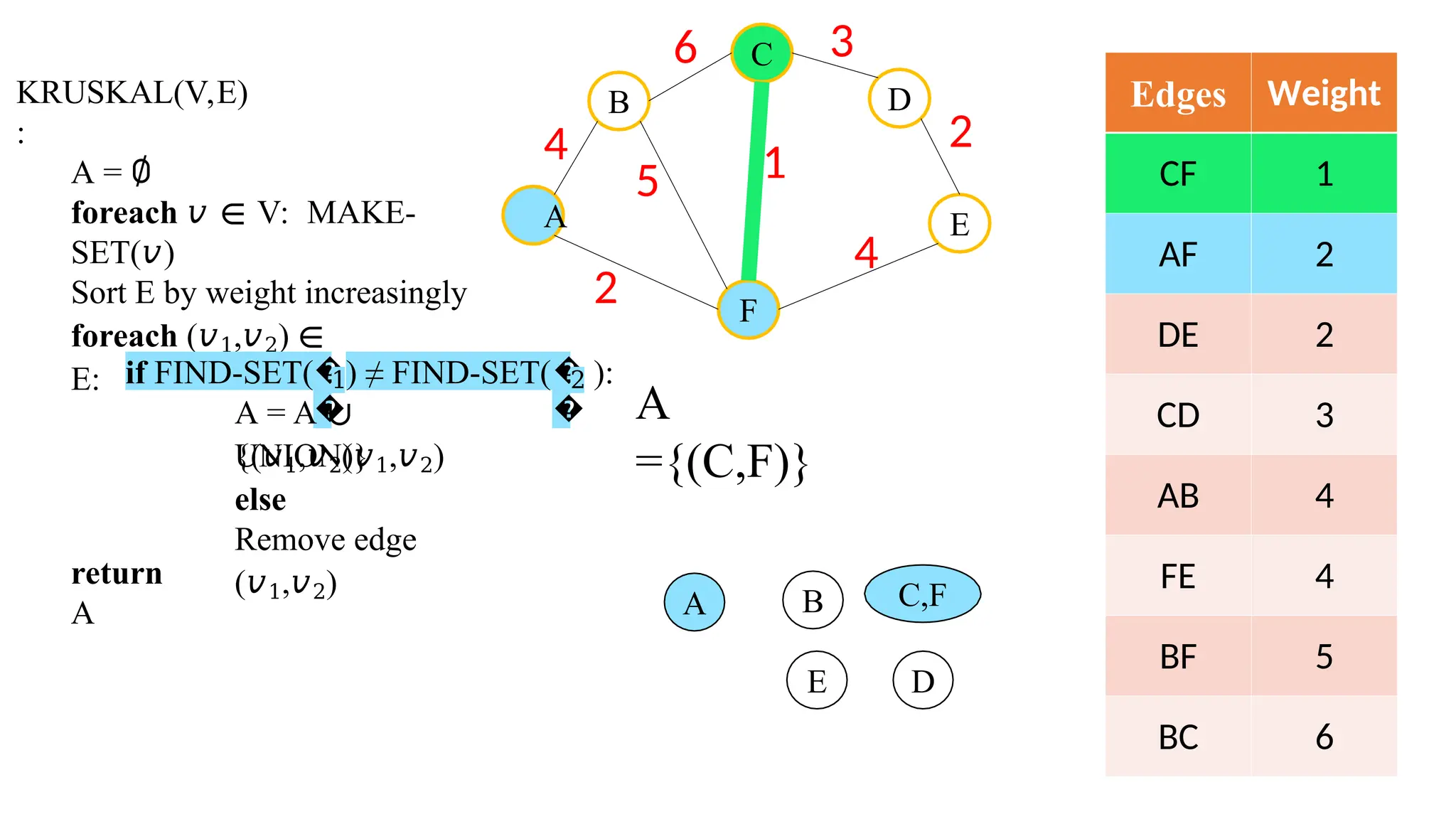
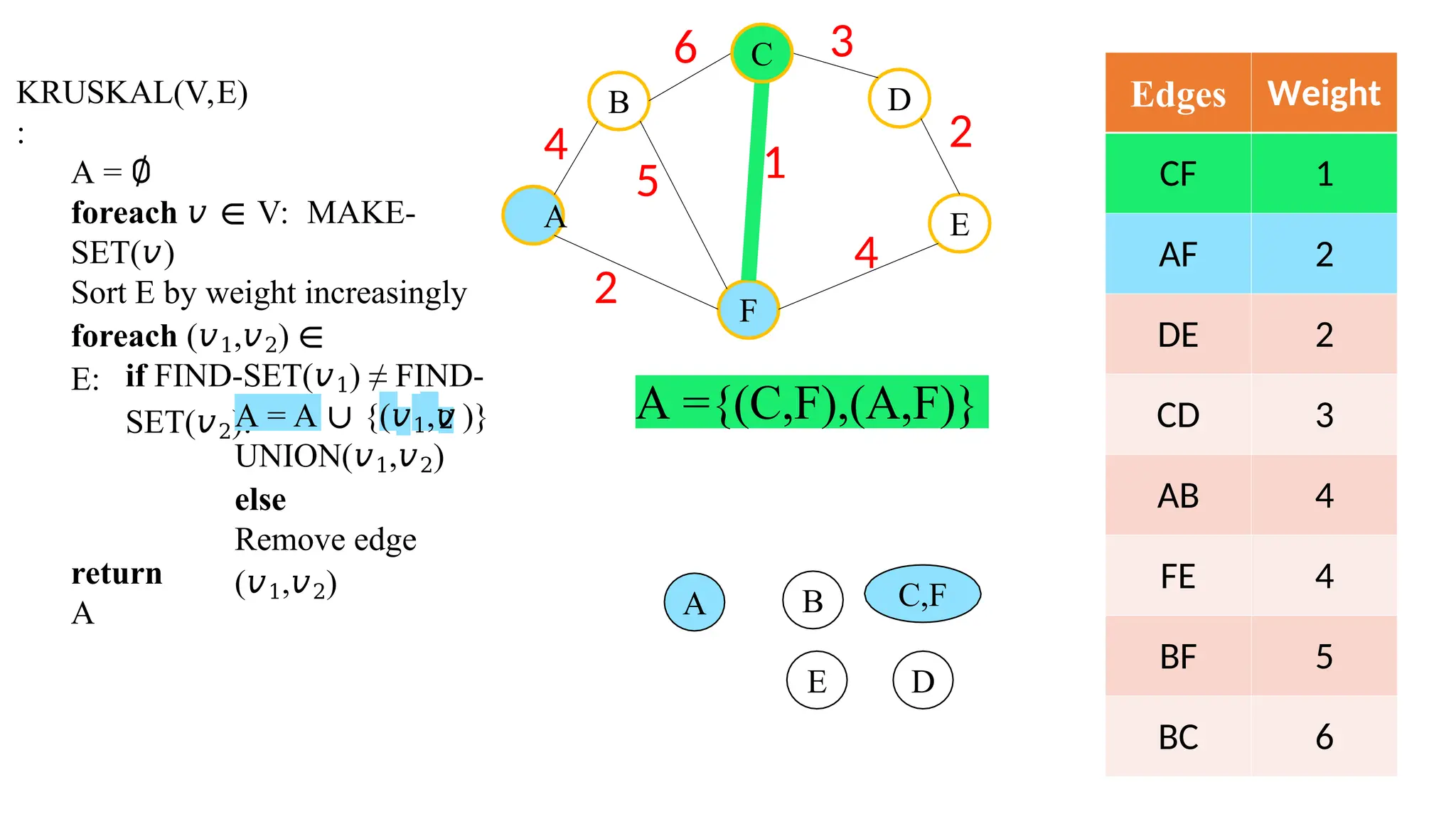
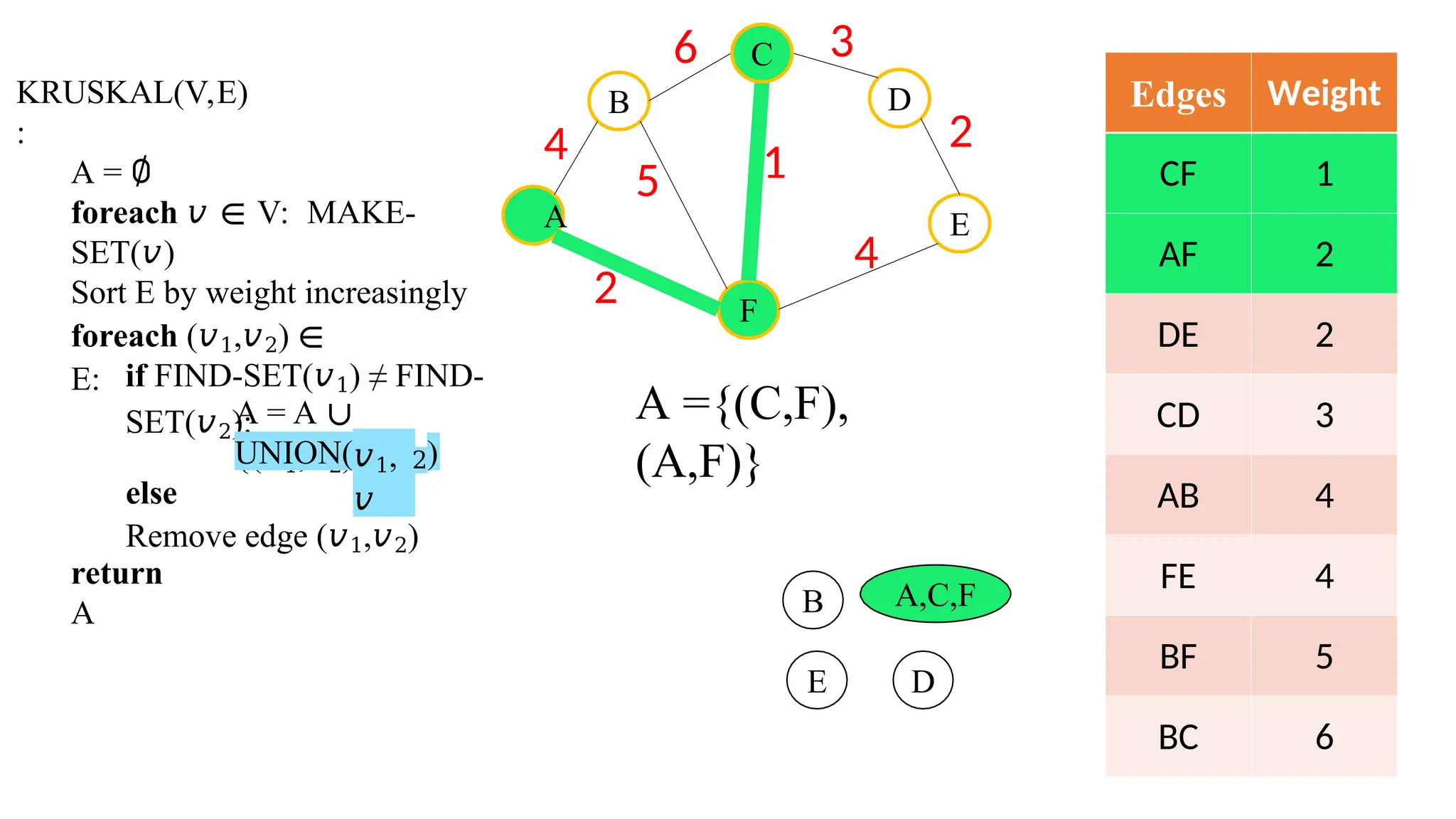
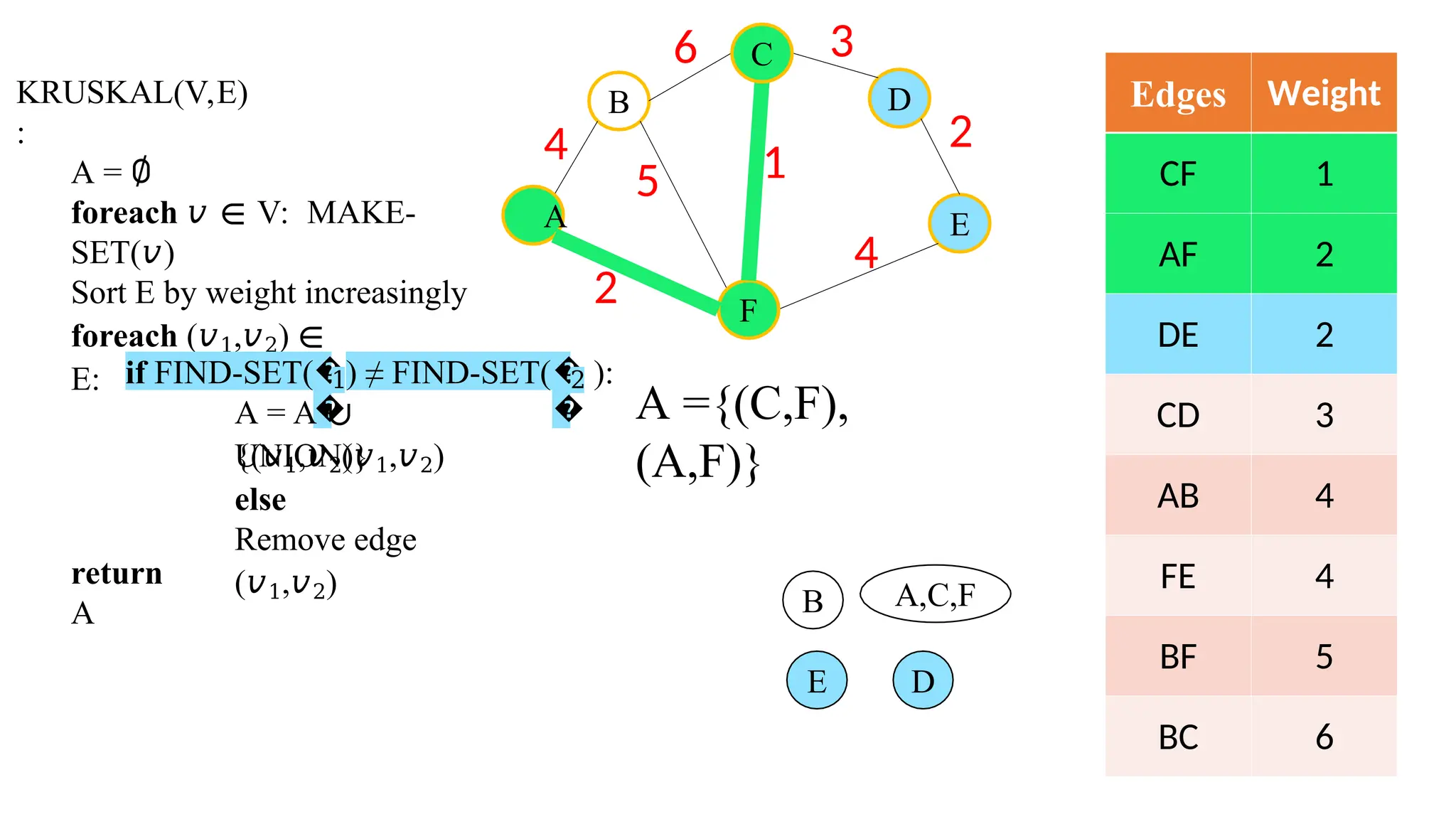
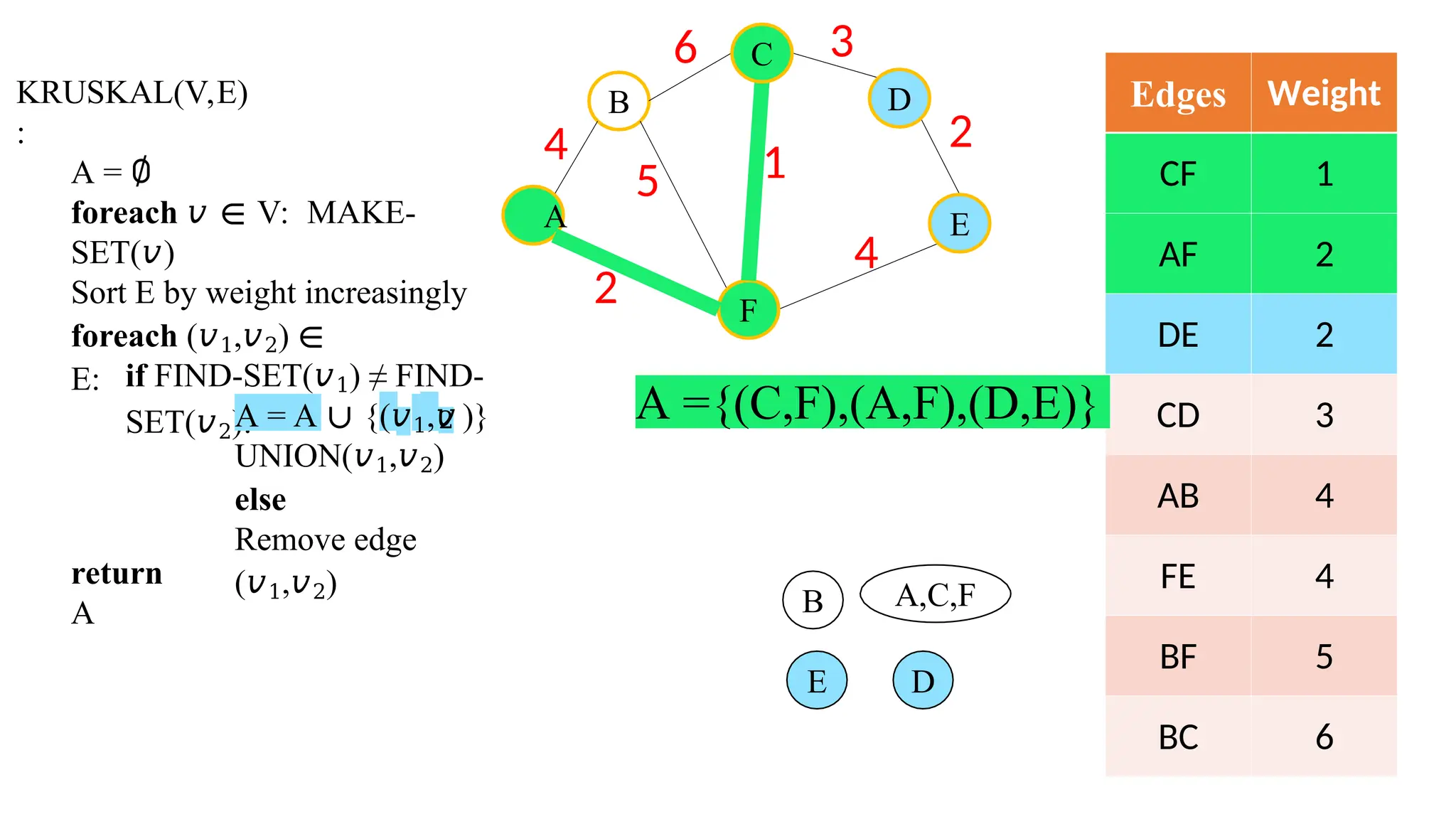
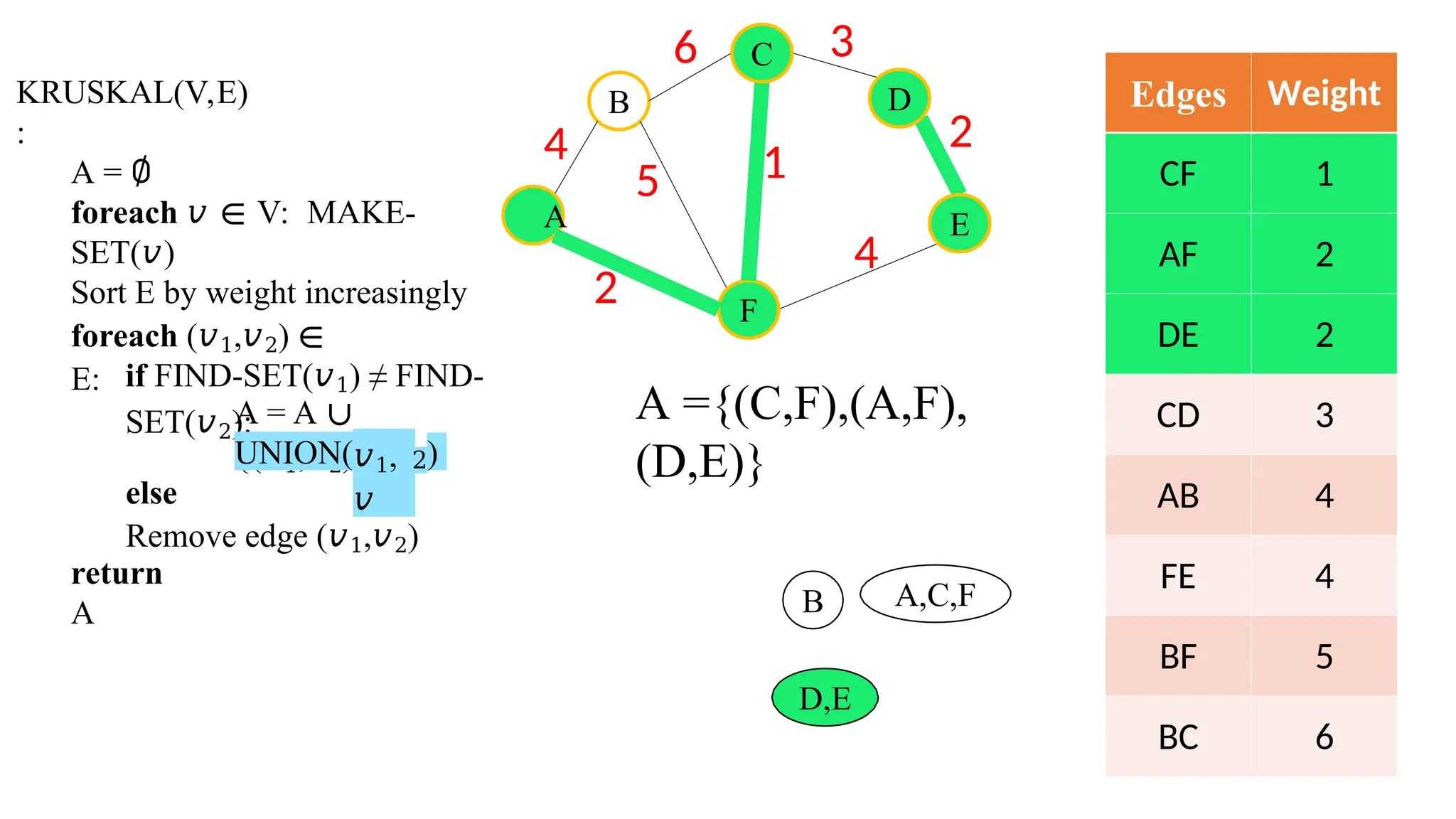
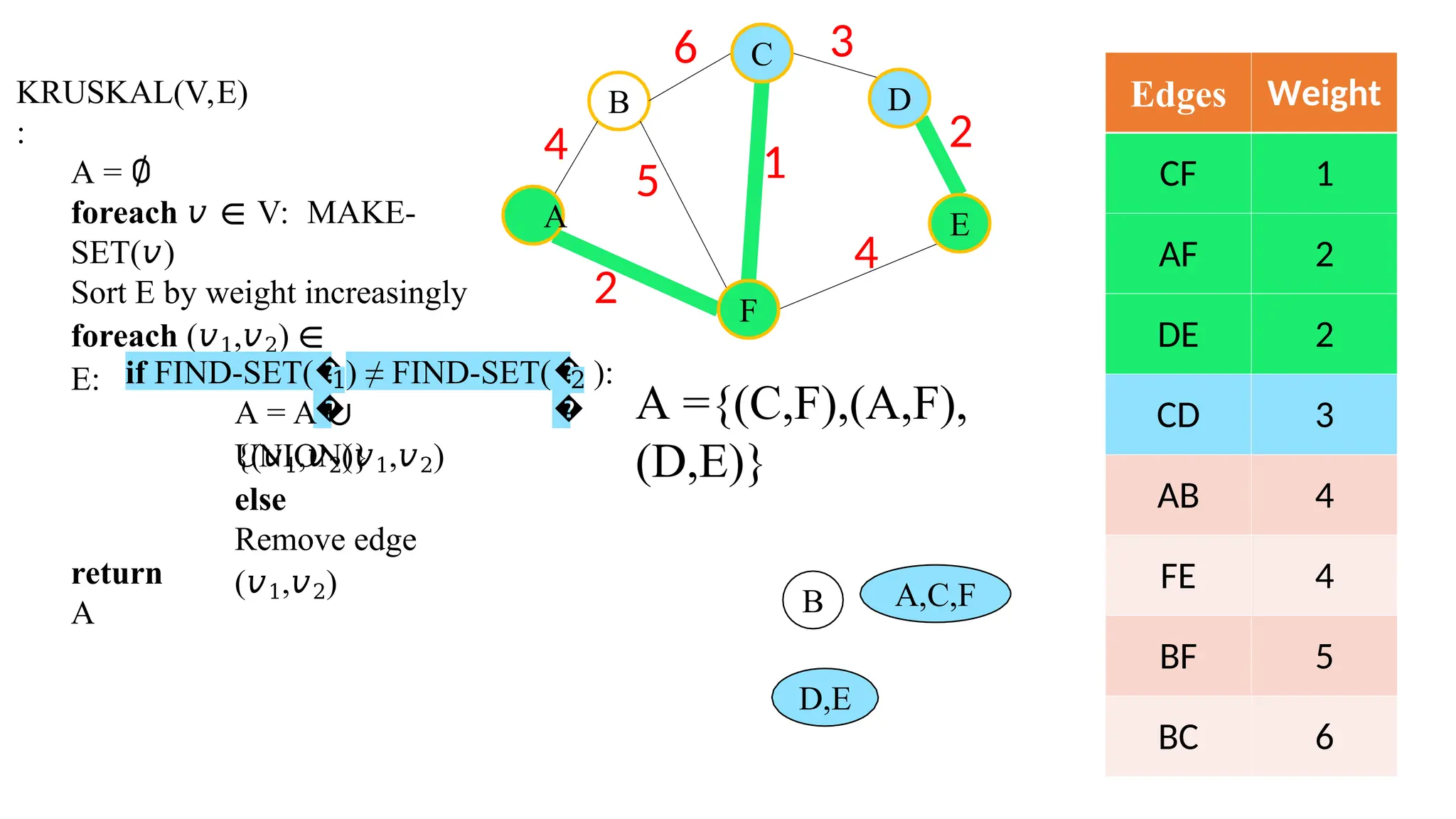
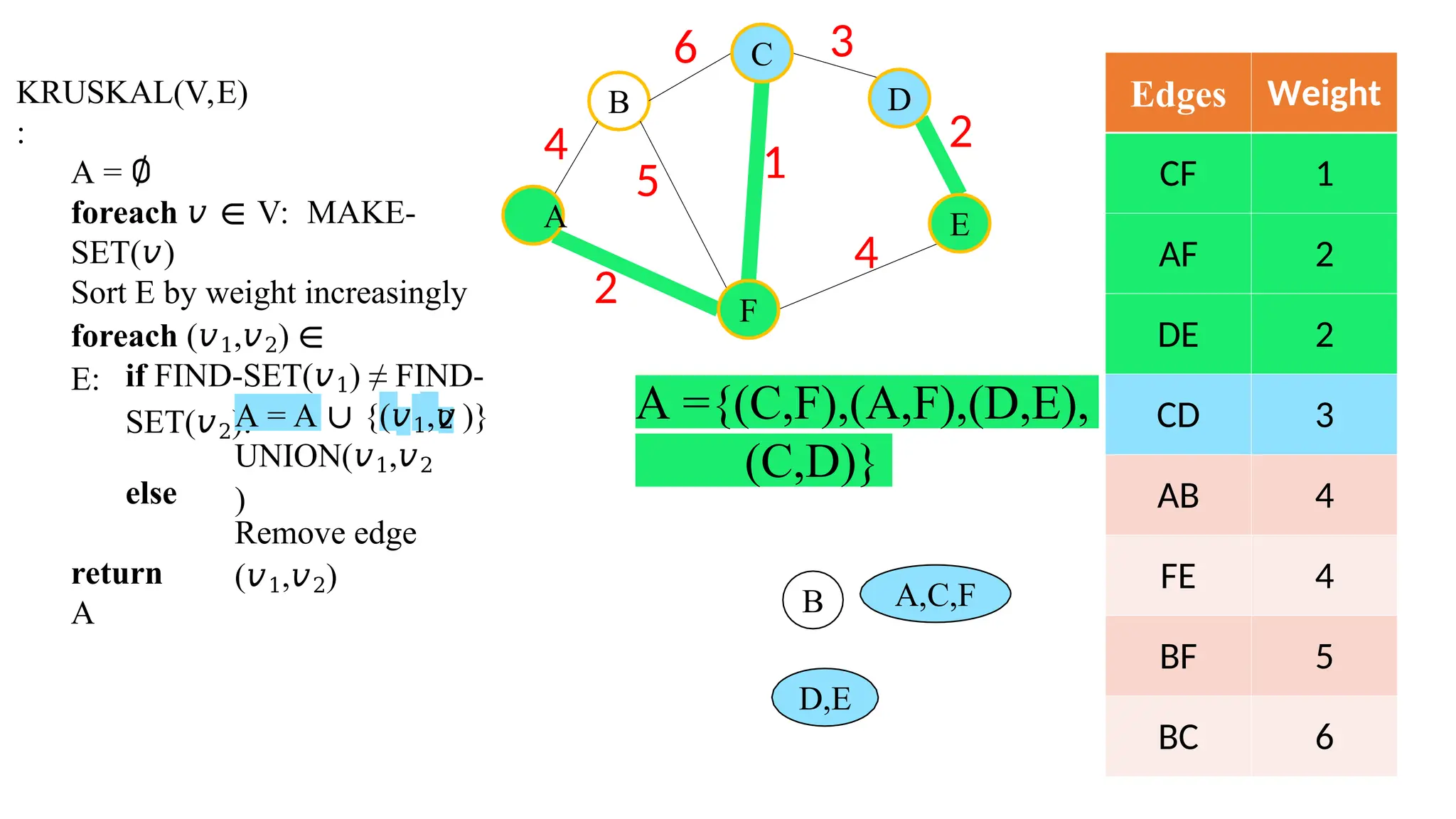
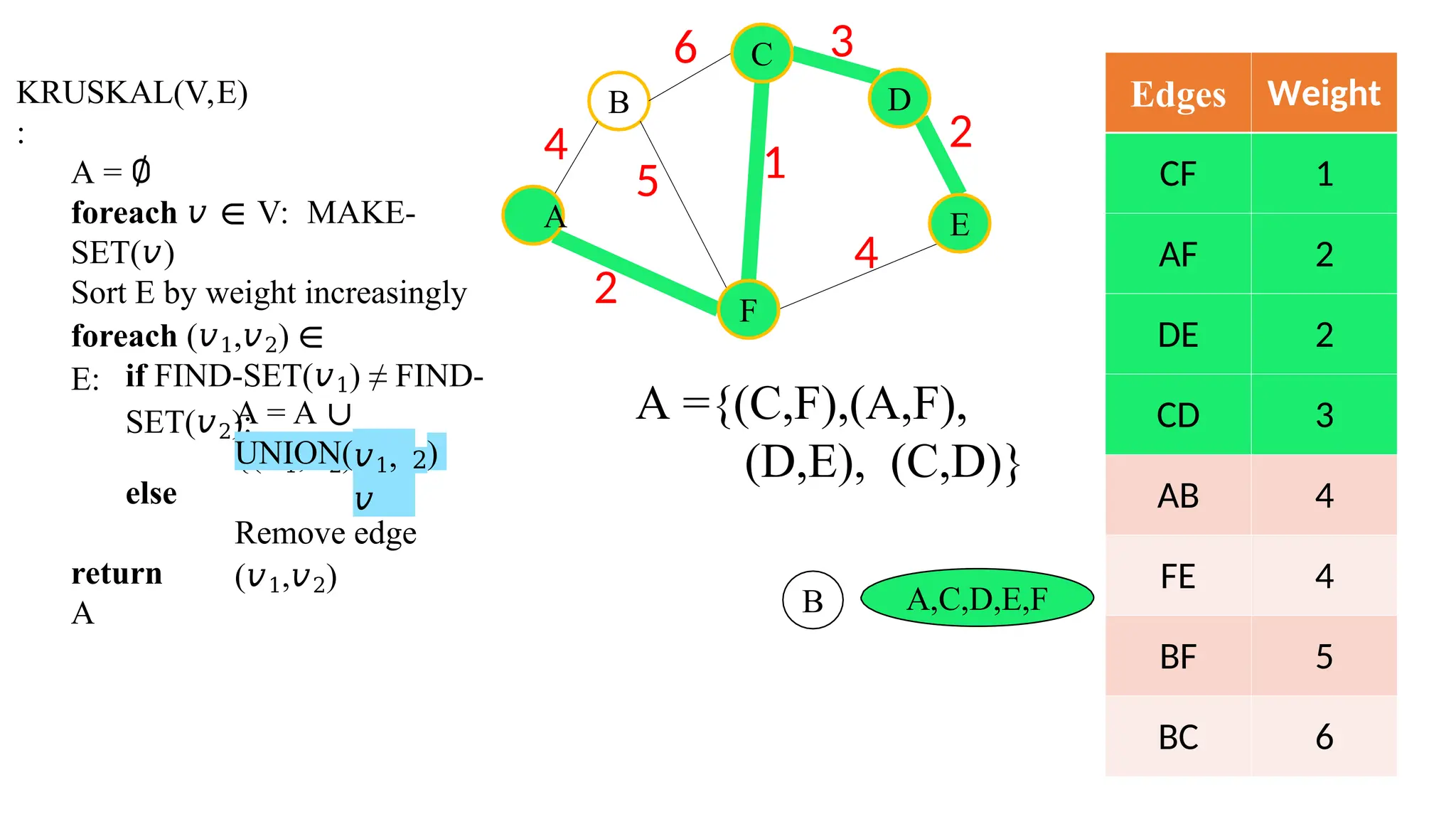
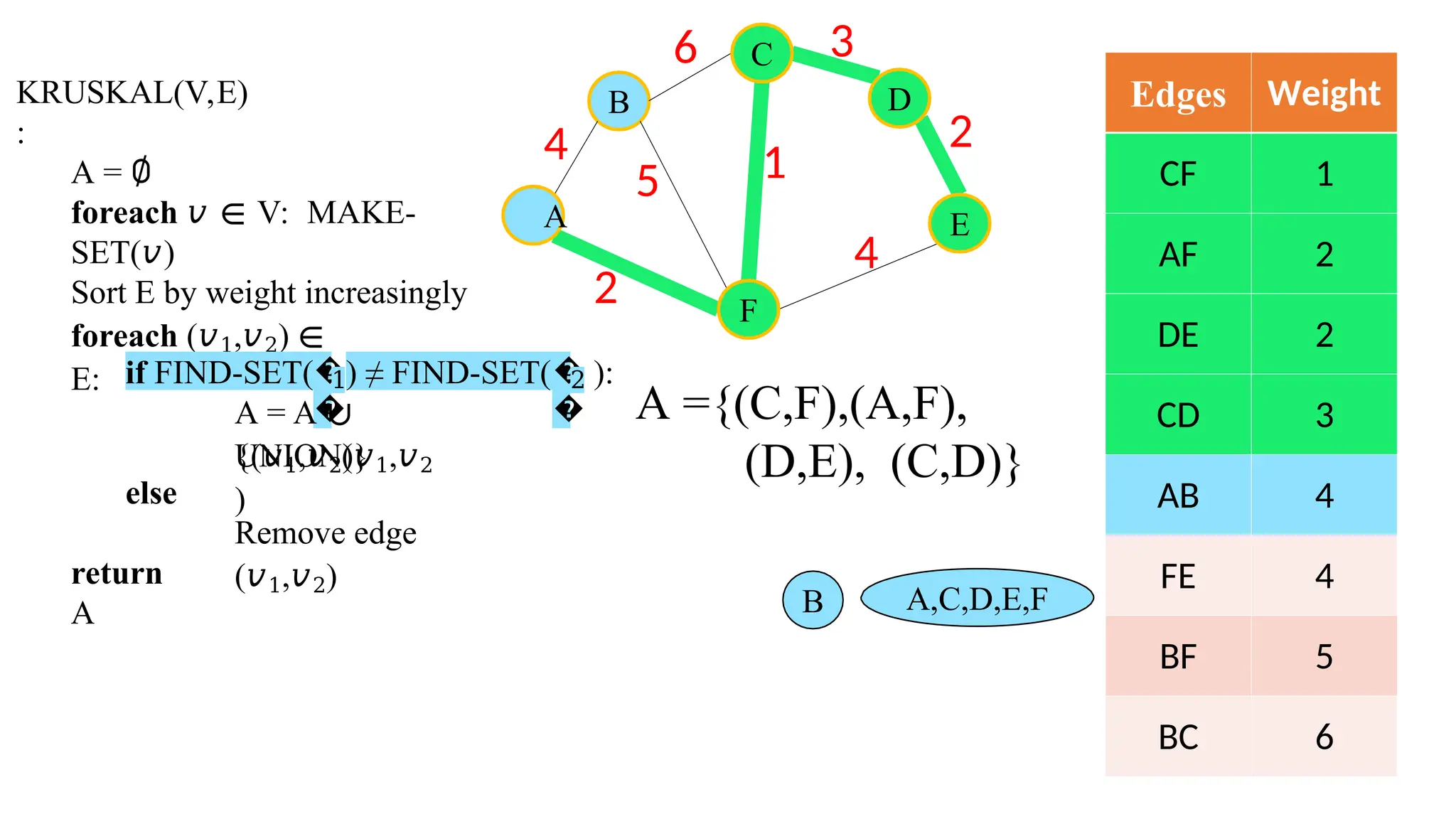
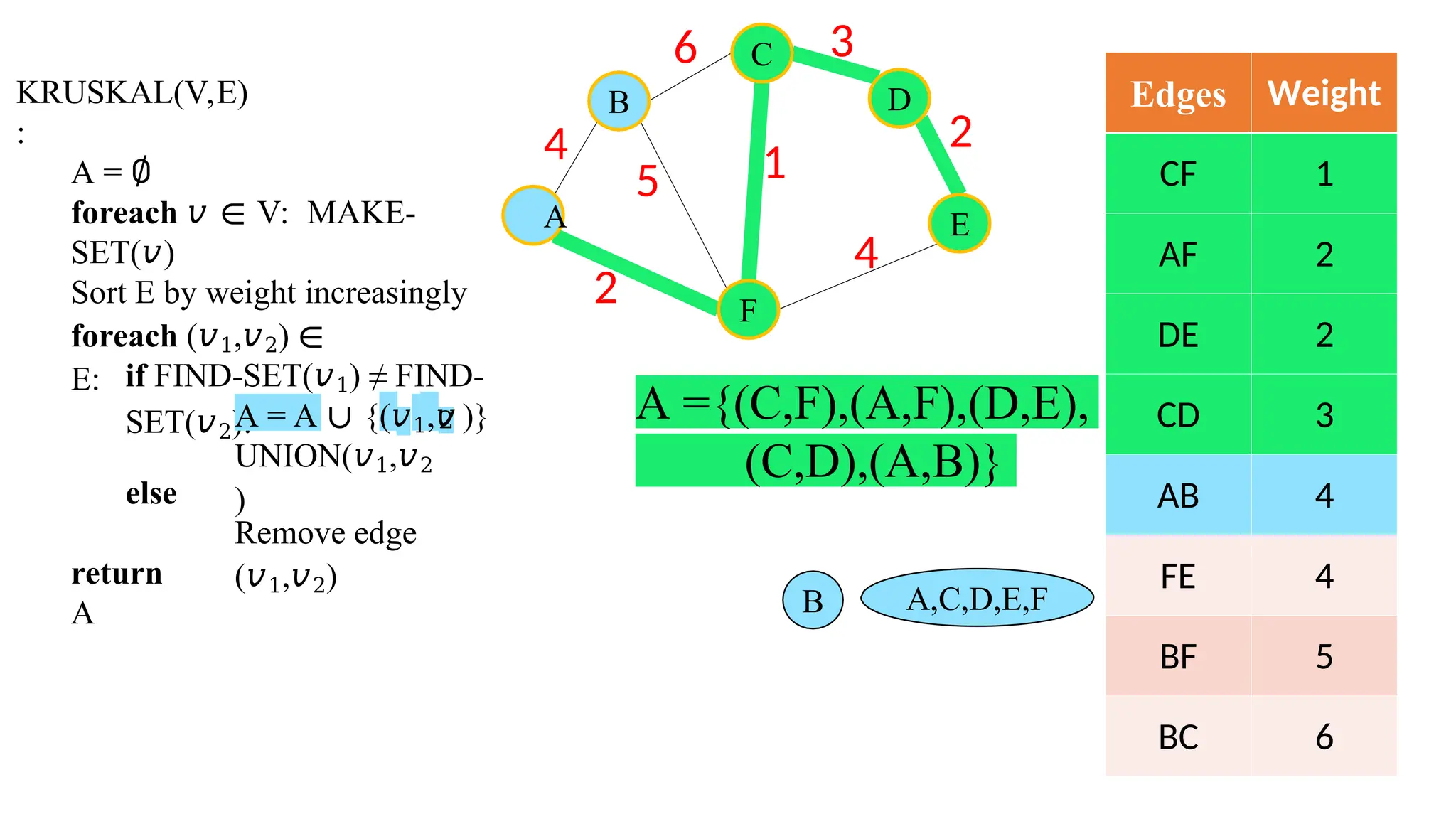
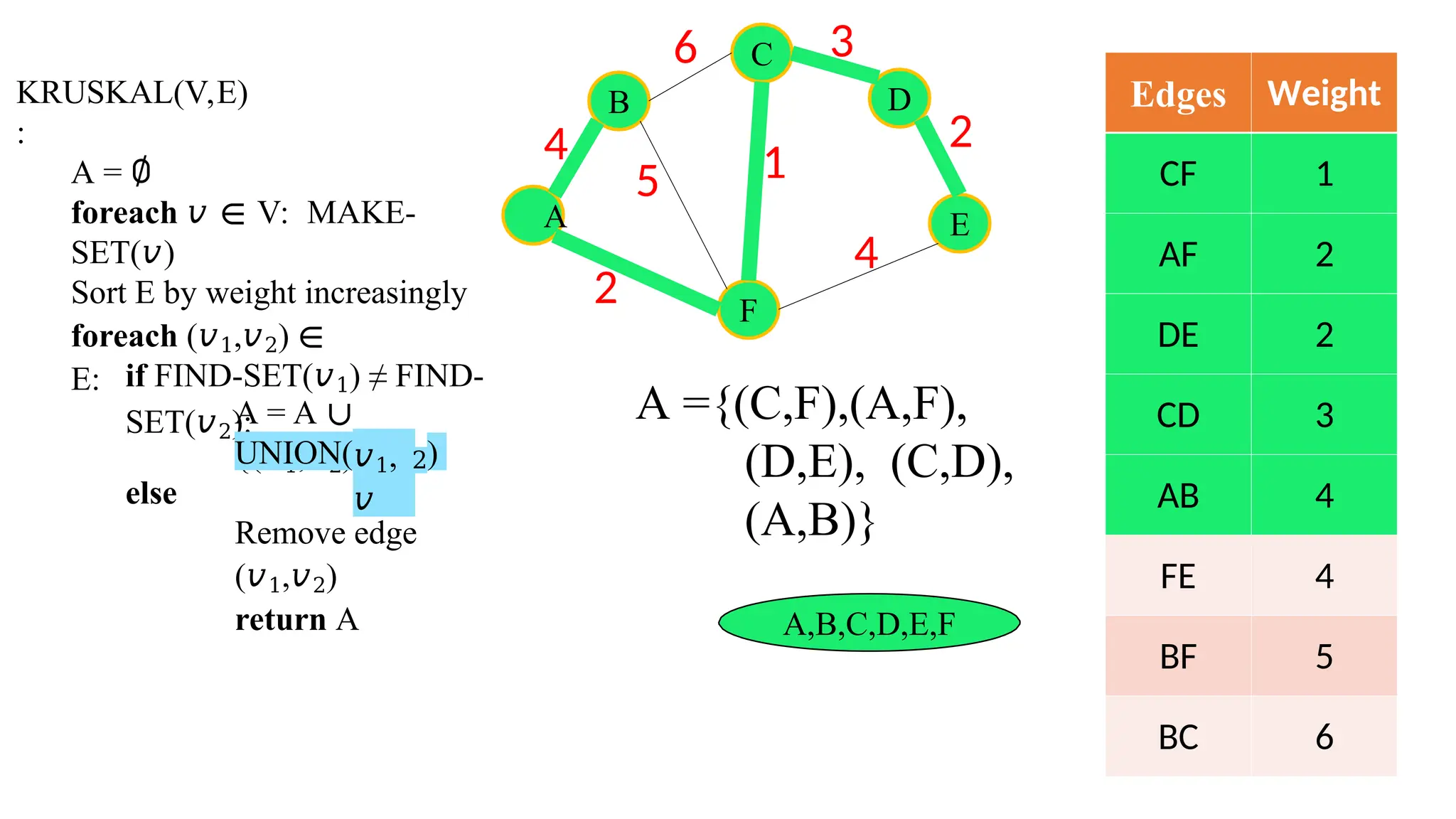
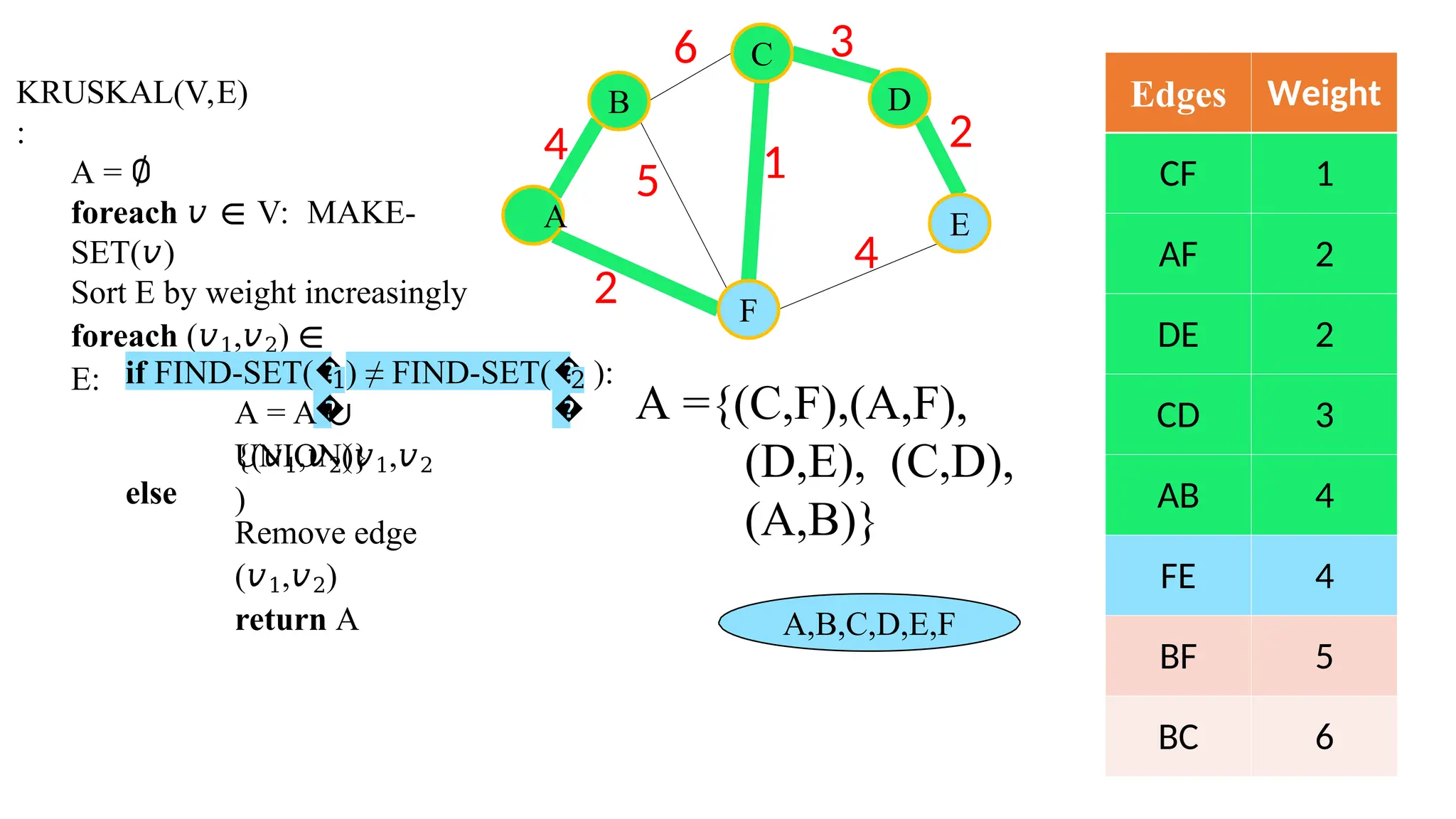
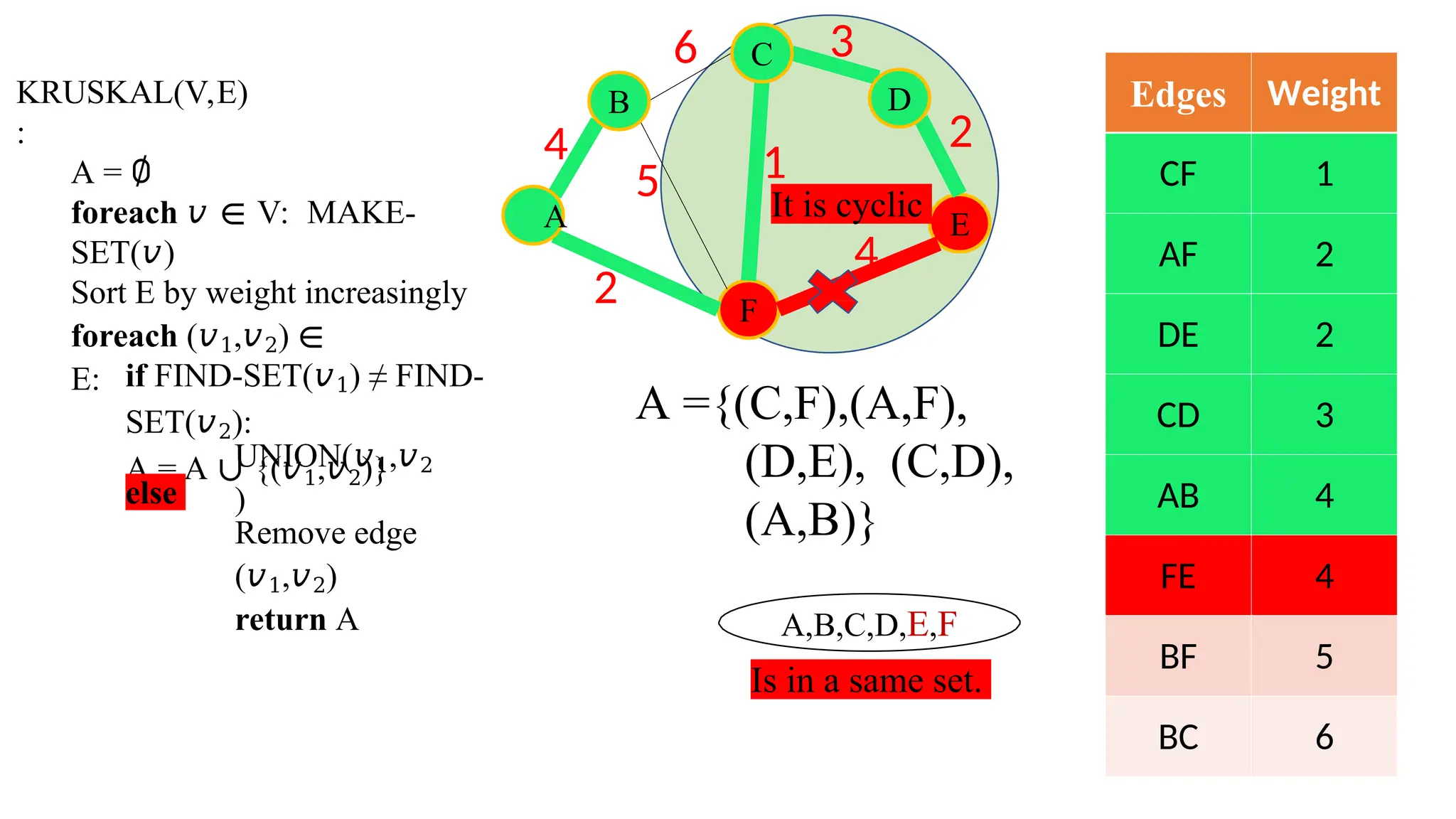
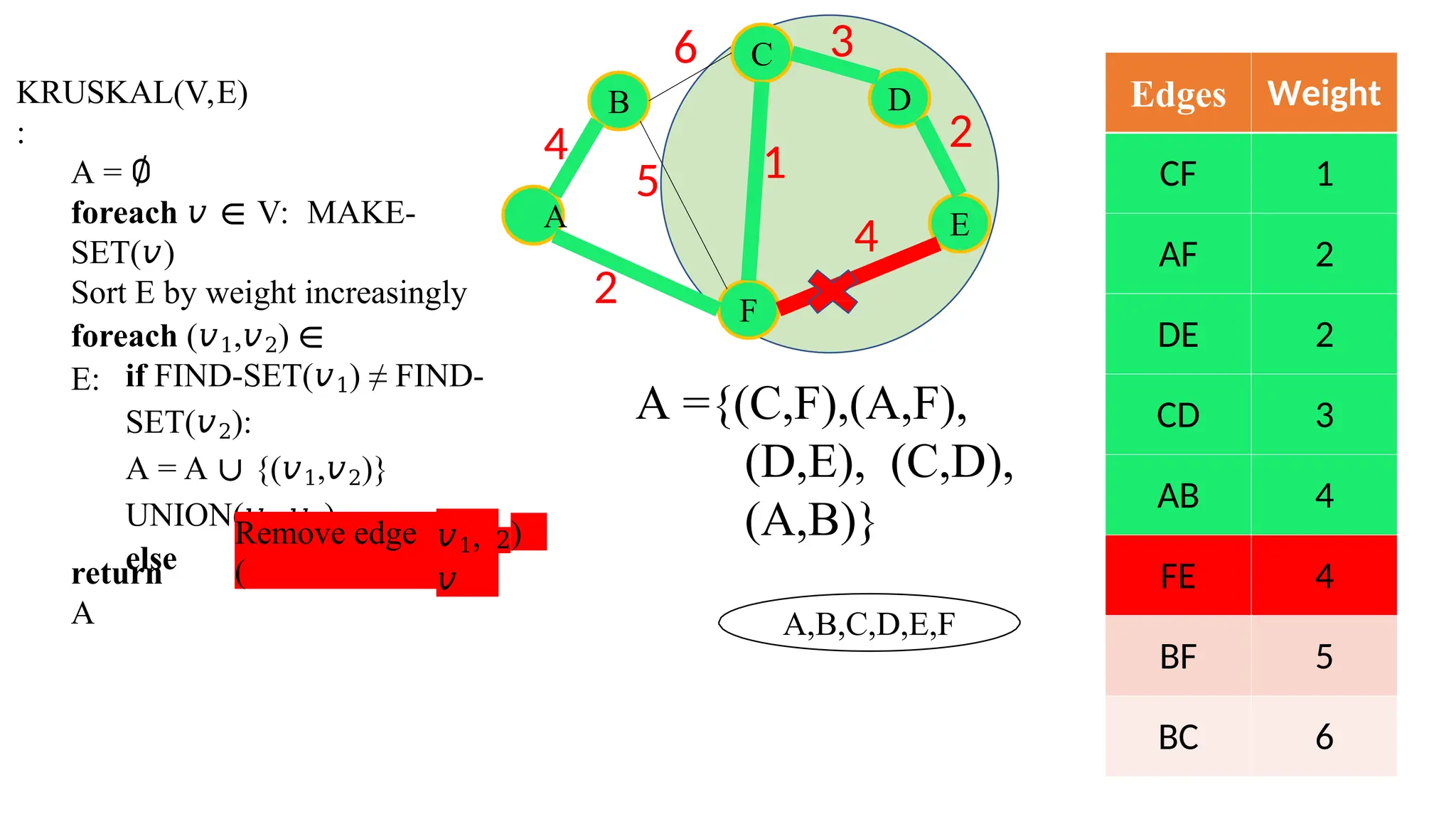
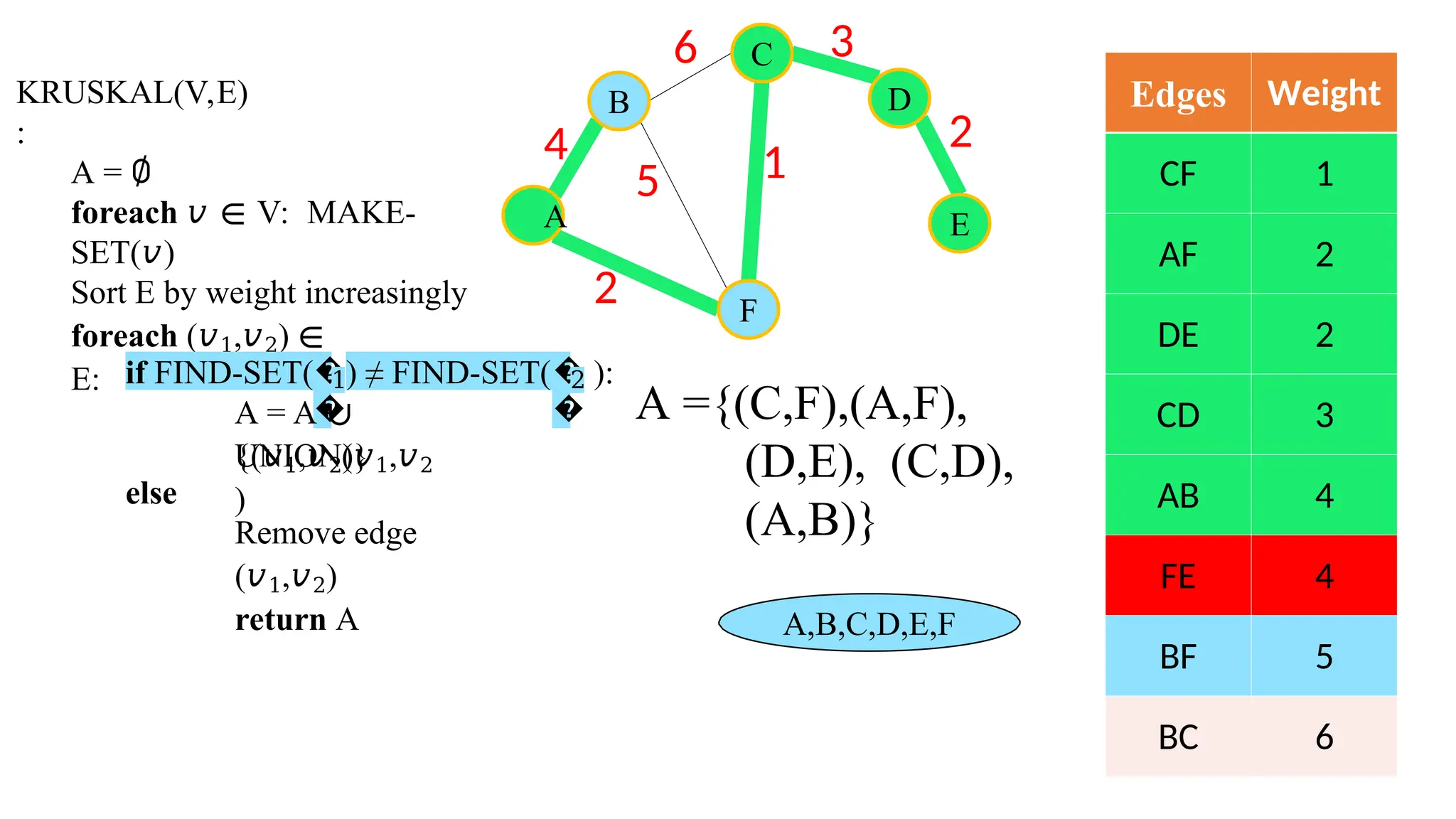
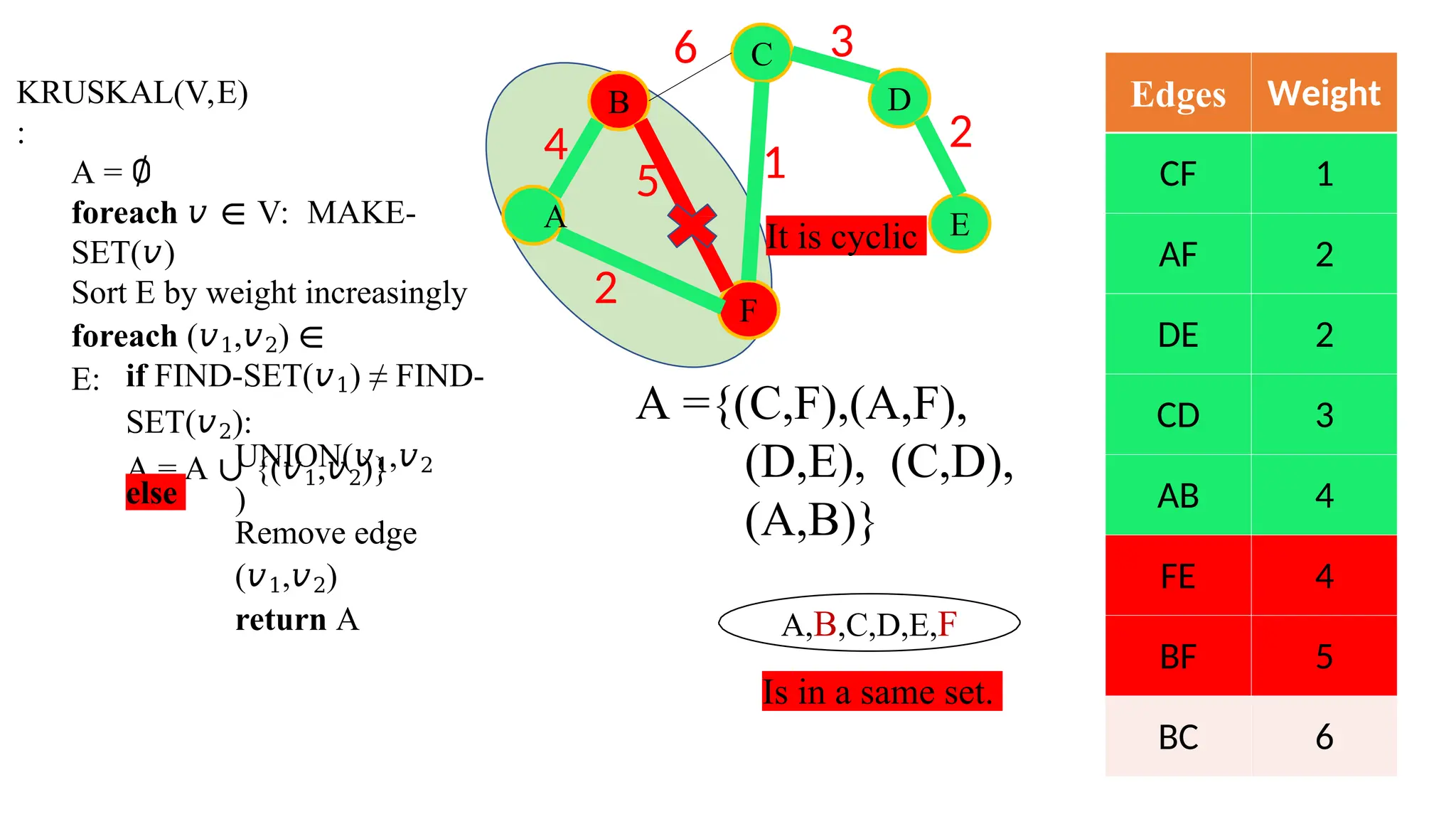
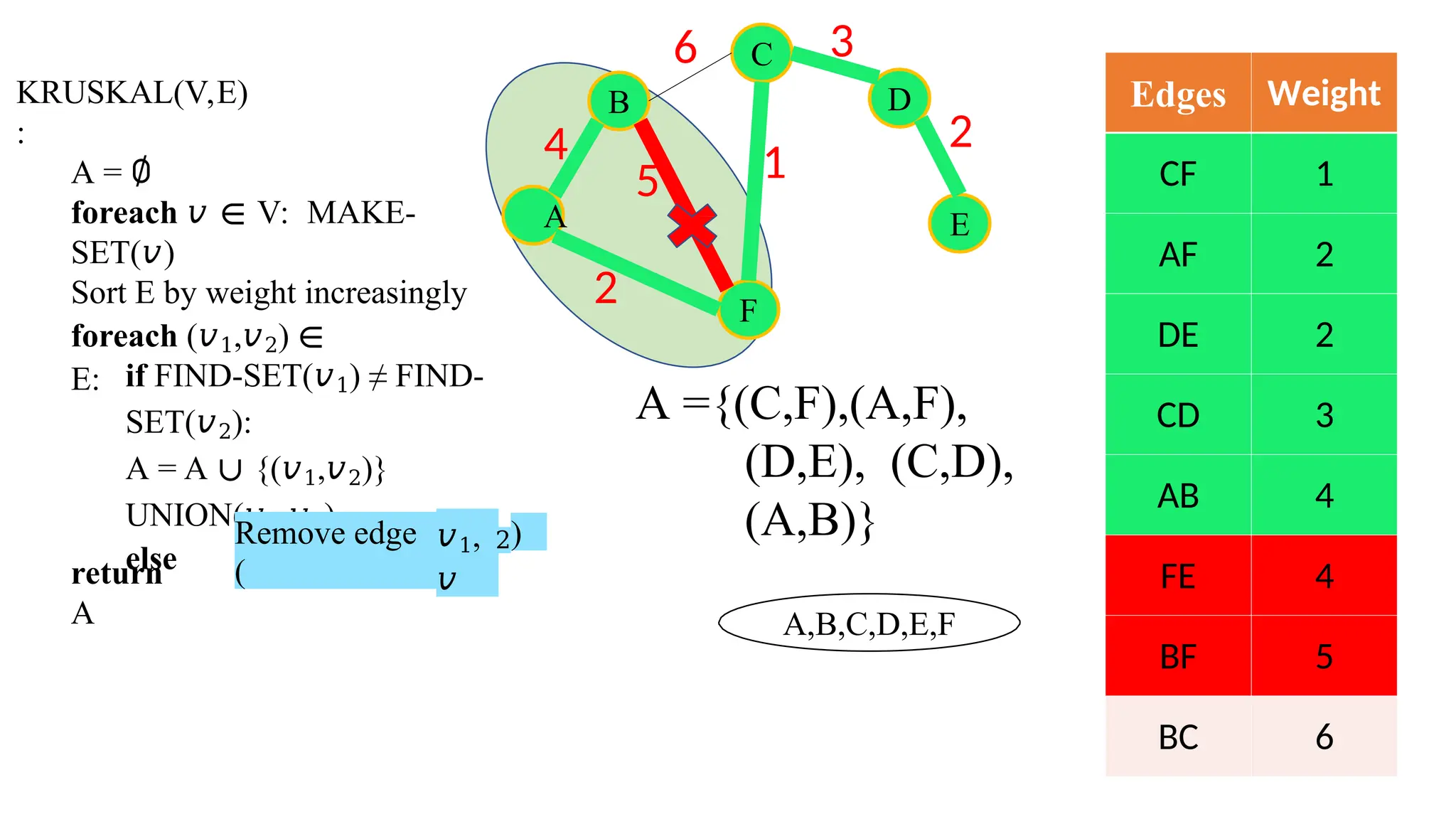
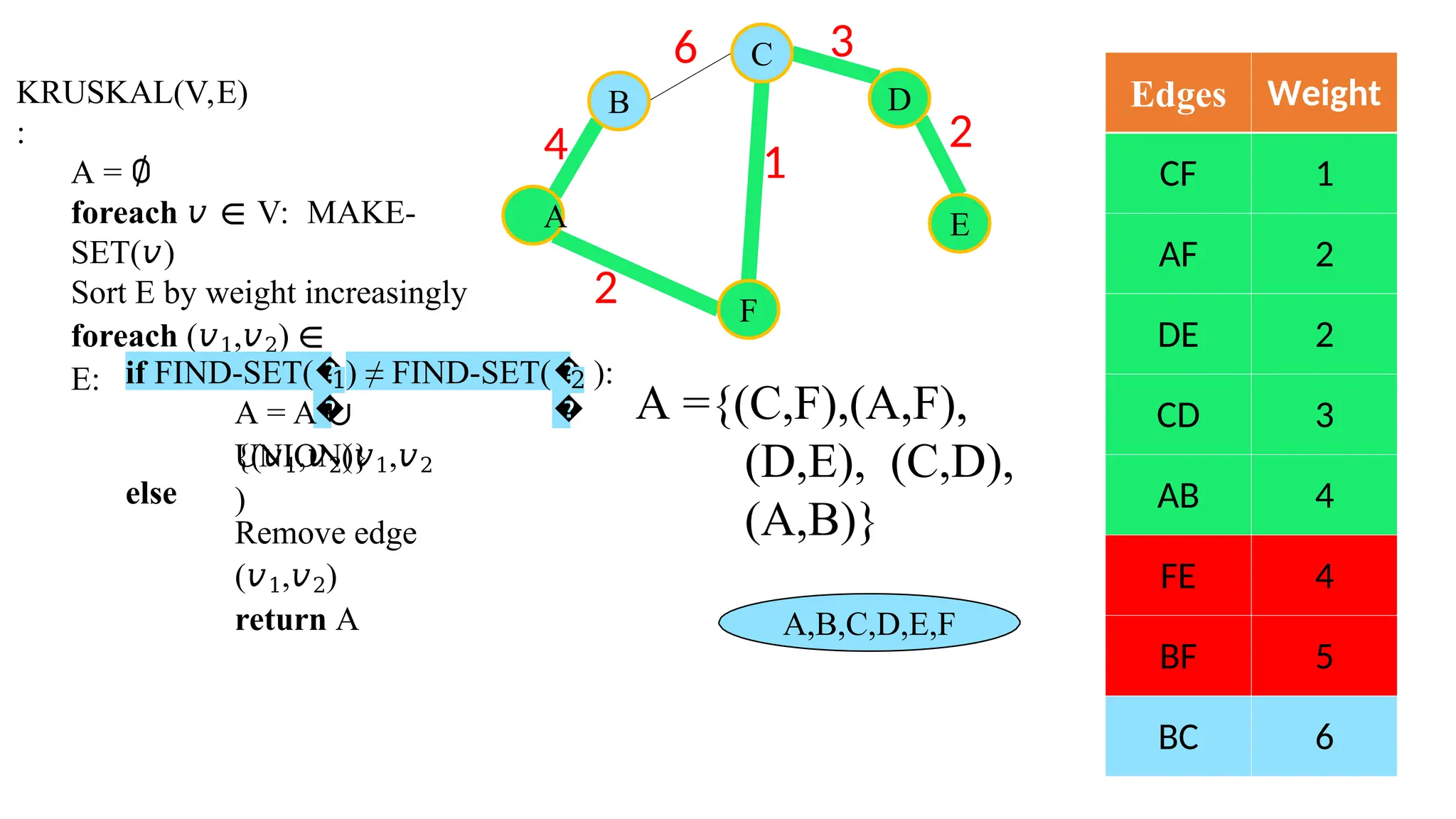
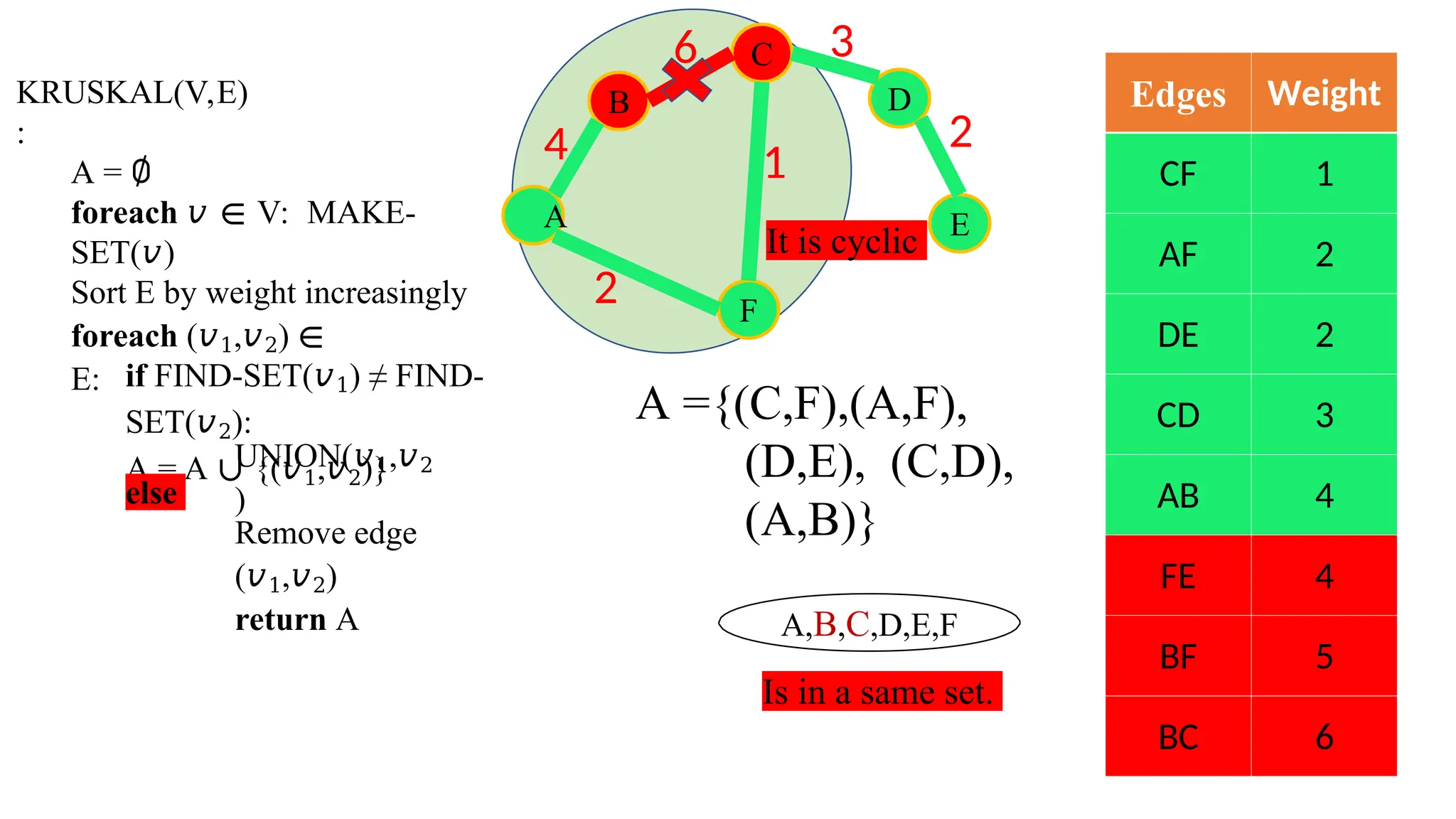
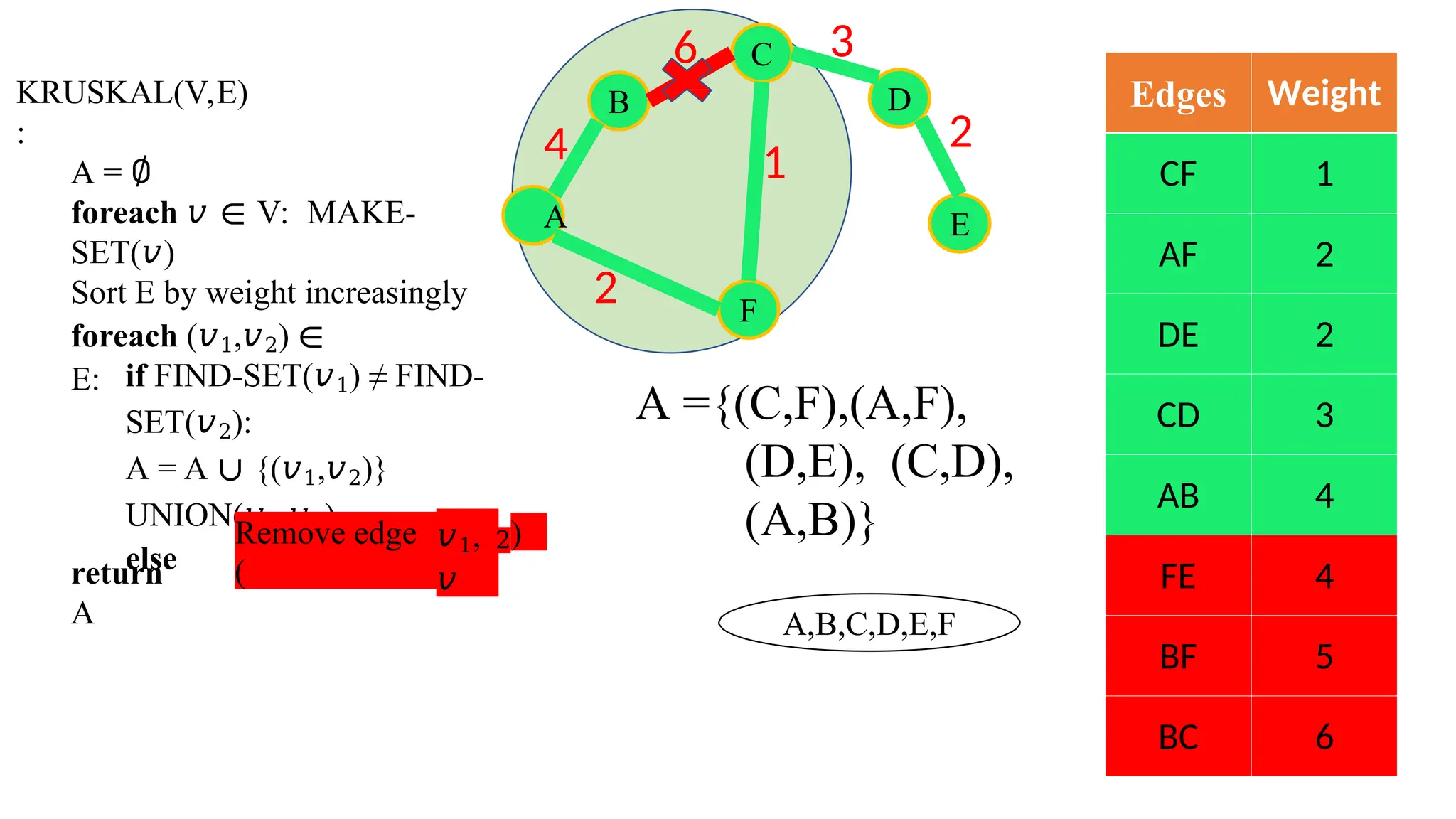
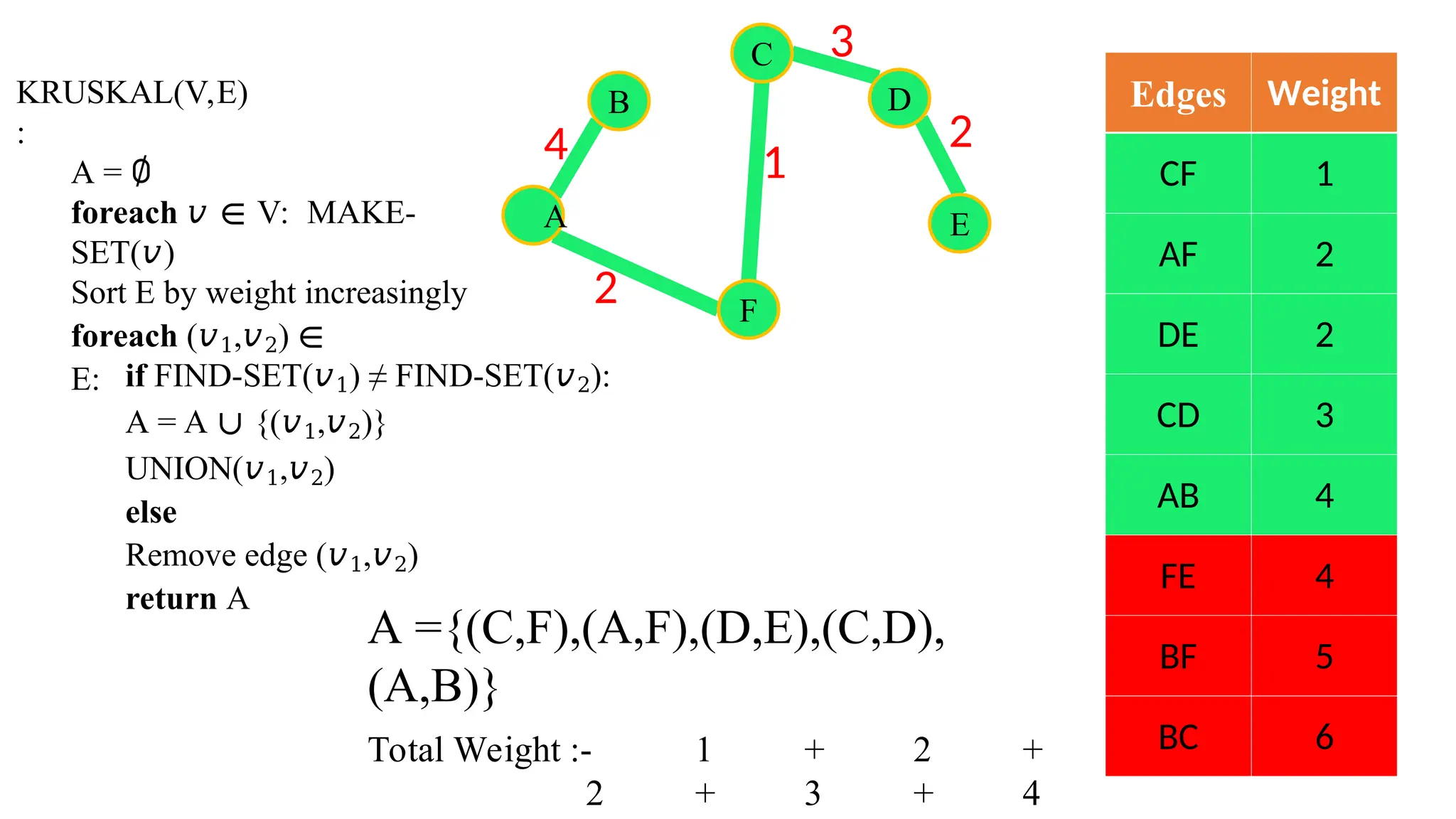
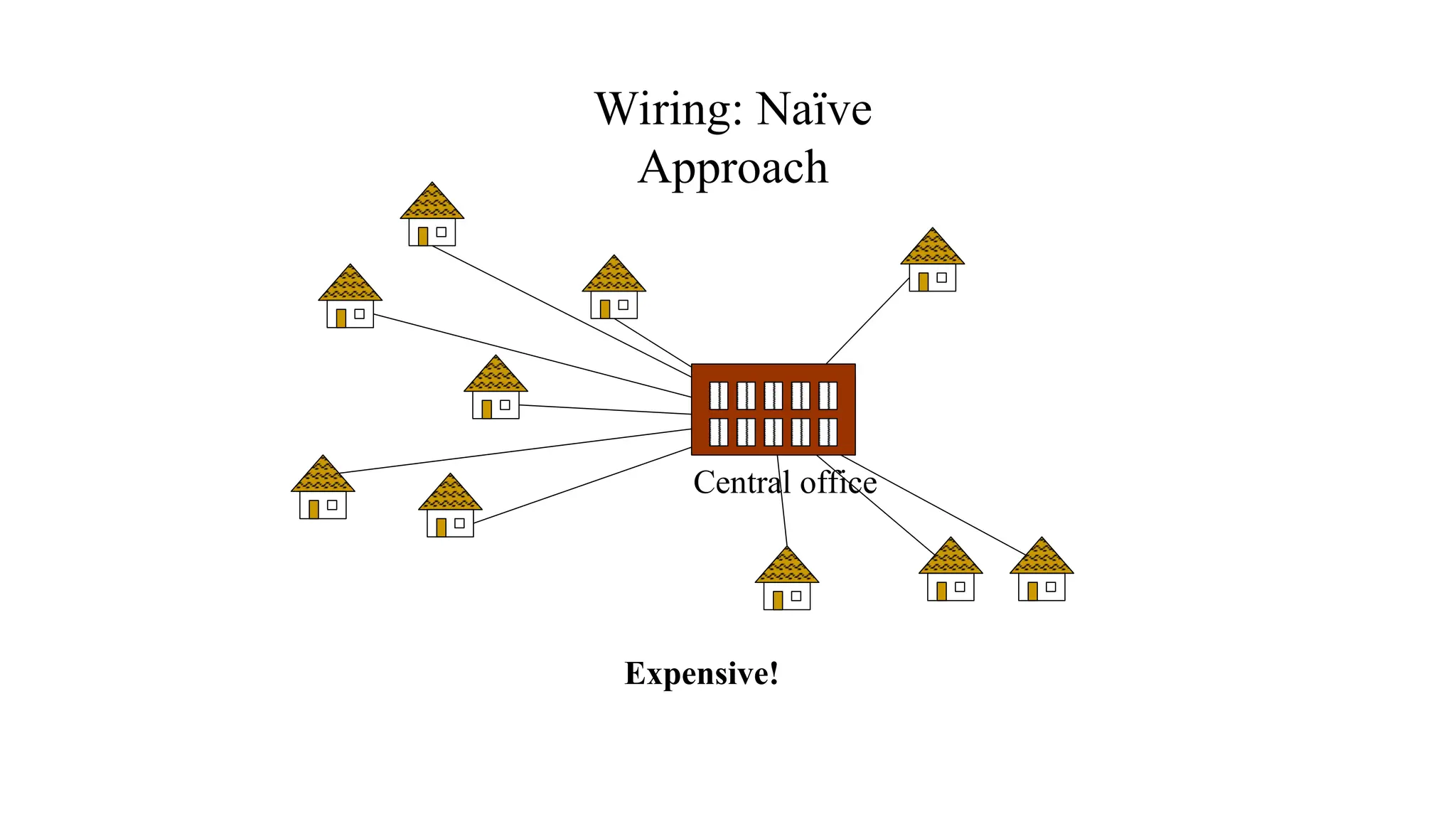
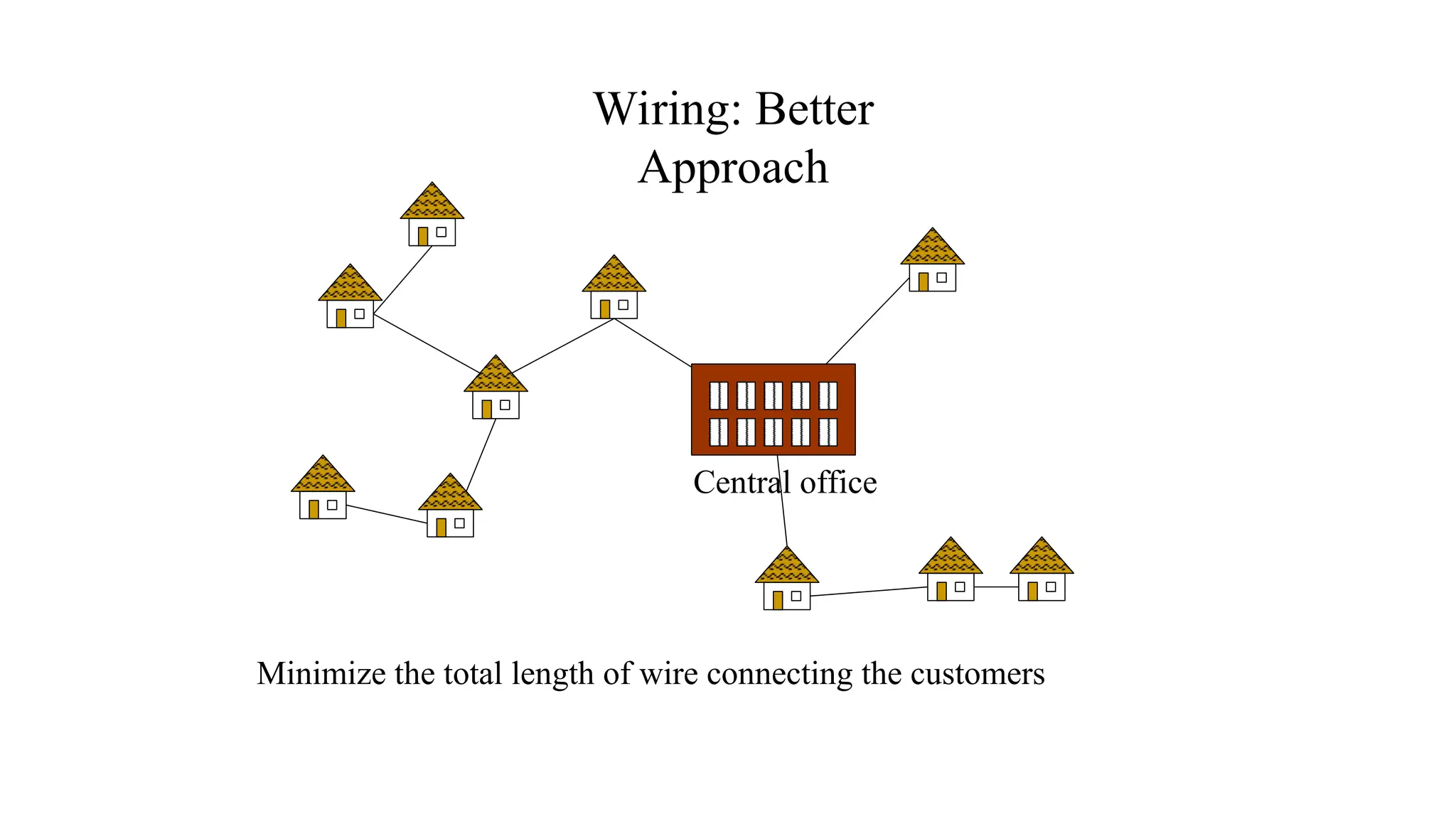
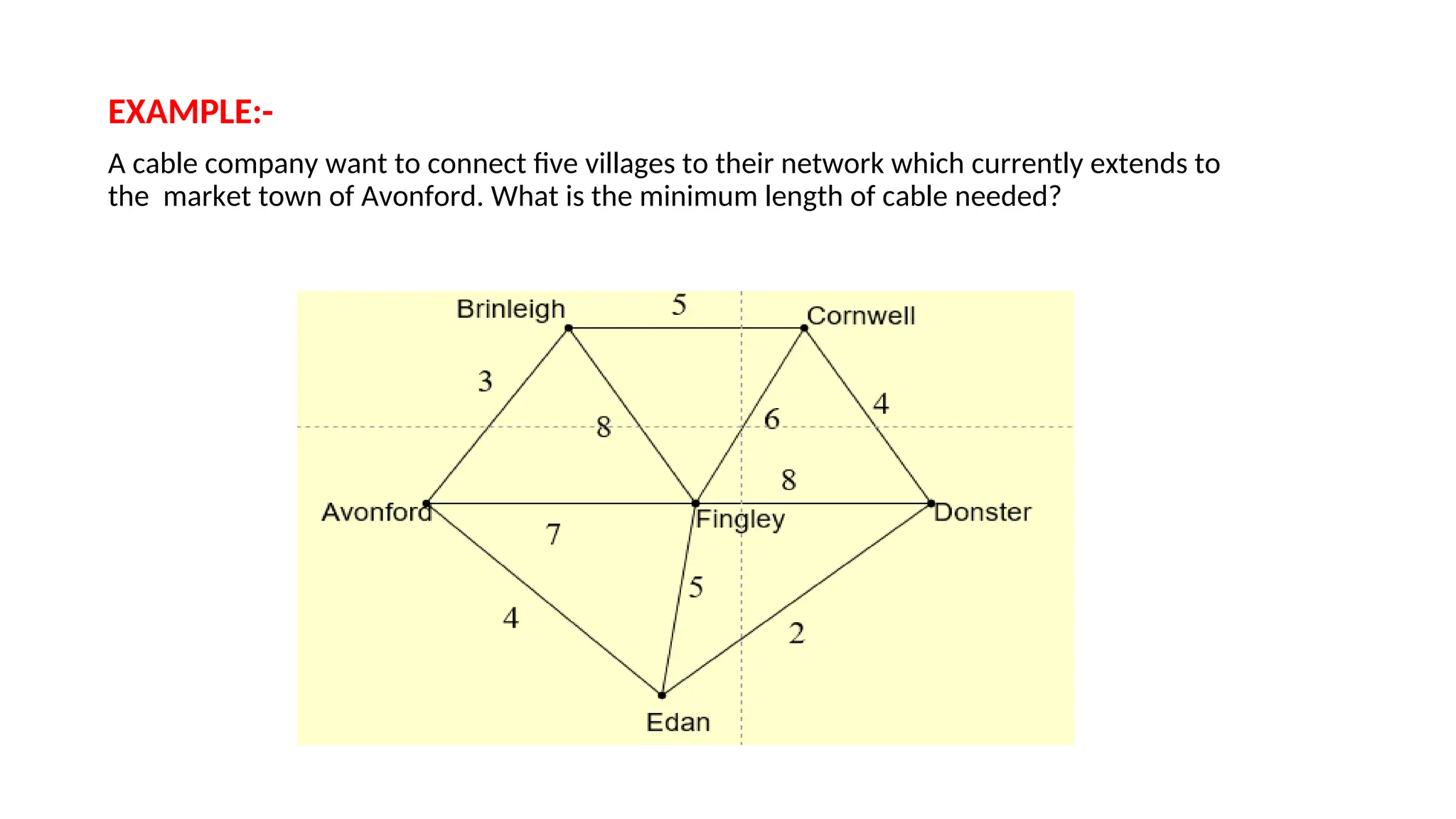
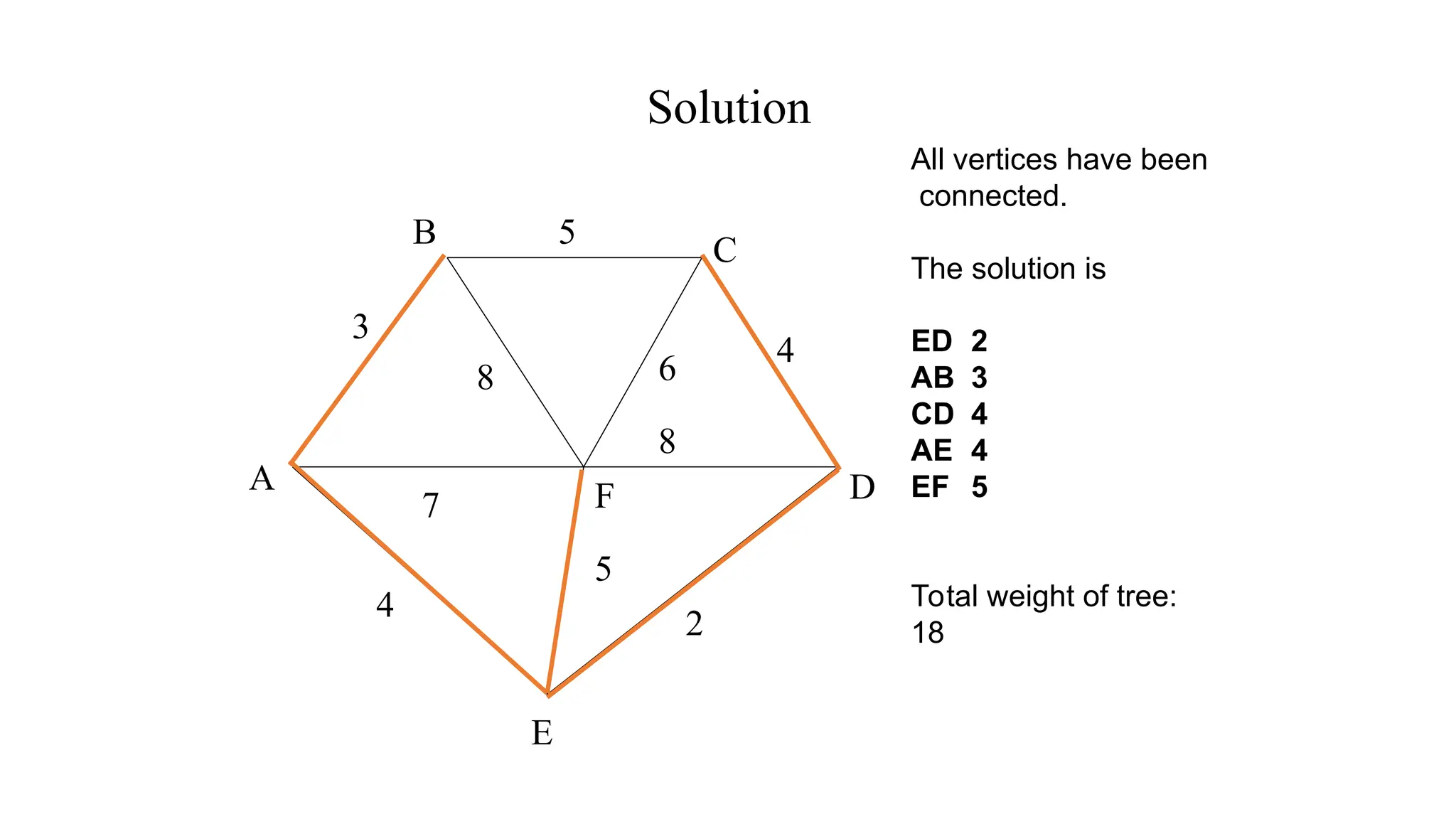
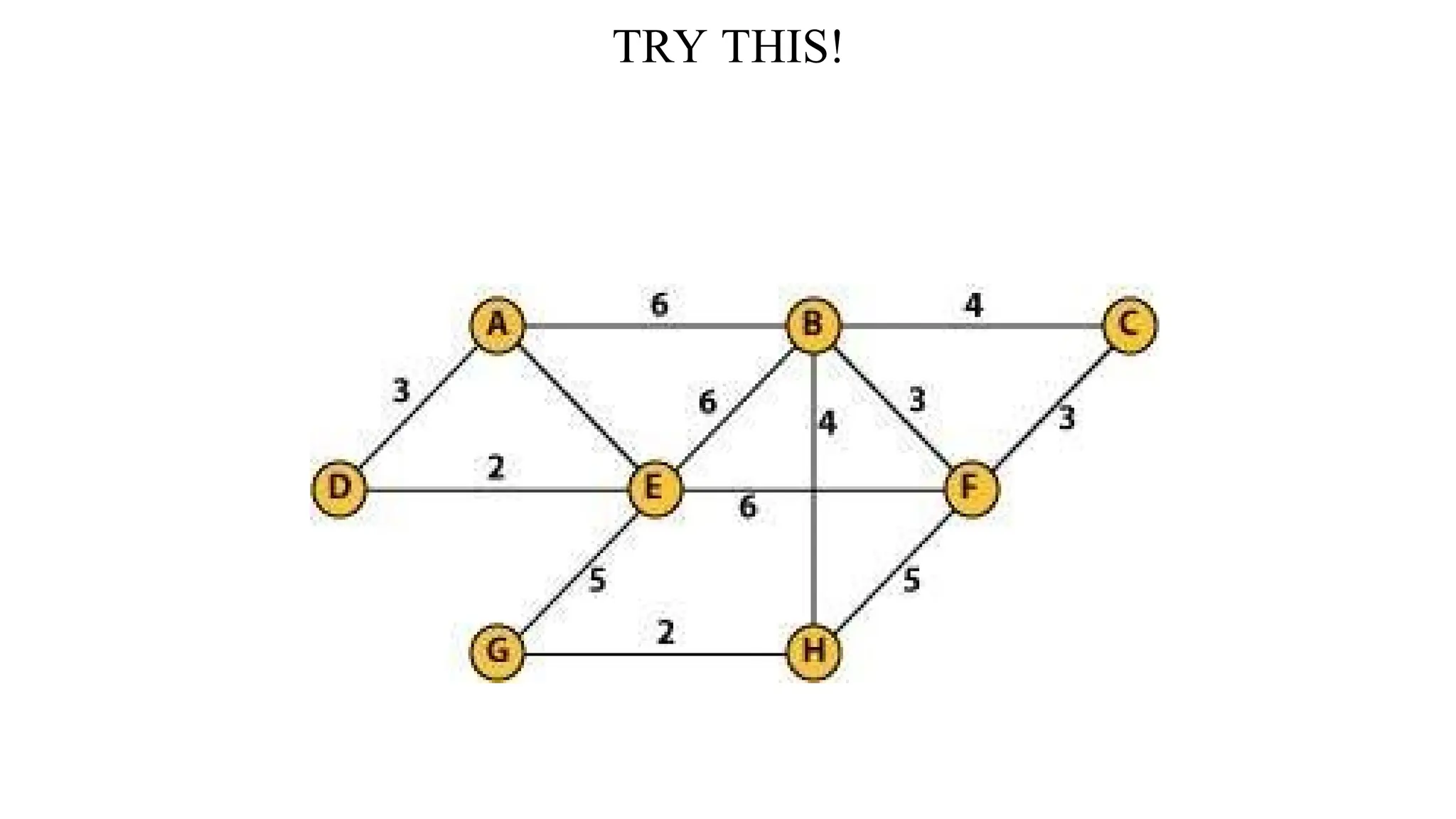
kruskal Algorithm in Algorithm for CS St

Greedy Algorithm
Kruskal’s Algorithm for Computing
MSTs

Tre
e
A tree is a graph with the following properties:
•The graph is connected (can go from anywhere to
anywhere)
•There are no cycles(acyclic)
Graphs that are not trees
Tree

Minimum Spanning Tree
(MST)
3
Let G=(V,E) be an undirected connected graph.
A sub graph T=(V,E’) of G is a spanning tree of G if :-
•T is a tree (i.e., it is acyclic)
•T covers all the vertices V
• contains |V| - 1 edges
•T has minimum total weight
•A single graph can have many different spanning trees.

Connected undirected
graph
Spanning
Tree

Kruskal’s
Algorithm
• It is a algorithm used to find a minimum cost spanning tree for connected weighted
undirected graph
• This algorithm first appeared in Proceedings of the American Mathematical
Society
in 1956, and was written by Joseph Kruskal
C D
Connected
Weighted
3
1
A B
4
6 2
5
A
1
B
2
C

Disjoint Sets
6
• A disjoint set is a data structure which keeps track of all elements that are separated
by
a number of disjoint (not connected) subsets.
• It supports three useful operations
• MAKE-SET(x): Make a new set with a single element x
• UNION (S1,S2): Merge the set S1 and set S2
• FIND-SET(x): Find the set containing the element x

Disjoint Sets
7
by
1 2 3
S1 S2 S3
MAKE-SET(1), MAKE-SET(2), MAKE-
SET(3) creates new set S1,S2,S3

Disjoint Sets
8
by
1 2
UNION (1,2) merge set S1 and set
S2 to create set S4
1 2 3
S4
S1 S2 S3
MAKE-SET(1), MAKE-SET(2), MAKE-
SET(3) creates new set S1,S2,S3

Disjoint Sets
by
a number of disjoint (not connected) subsets
1 2
UNION (1,2) merge set S1 and set S2
to create set S49
1 2 3
S4
FIND-SET(2) returns set S4
1 2
S4
S1 S2 S3
MAKE-SET(1), MAKE-
SET(2), MAKE-SET(3)
creates

KRUSKAL(V,E):
A = ∅
foreach 𝑣∈ V: MAKE-SET(𝑣)
Sort E by weight increasingly
foreach (𝑣1,𝑣2) ∈ E:
if FIND-SET(𝑣1) ≠ FIND-SET(𝑣2):
A = A ∪ {(𝑣1,𝑣2)} UNION(𝑣1,𝑣2)
else
Remove edge (𝑣1,𝑣2)
return A
Kruskal’s
Algorithm

B
C
F
D
E
4
A
6 3
2
4
2
5 1
Edges Weight
AB 4
BC 6
CD 3
DE 2
EF 4
AF 2
BF 5
CF 1
KRUSKAL(V,E)
:
A = ∅
foreach 𝑣 ∈ V: MAKE-
SET(𝑣)
foreach (𝑣1,𝑣2) ∈
E: if FIND-SET(𝑣1) ≠ FIND-SET(𝑣2):
A = A ∪ {(𝑣1,𝑣2)}
UNION(𝑣1,𝑣2)
else
return A

KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
E: if FIND-SET(𝑣1) ≠ FIND-
SET(𝑣2):
A = A ∪ {(𝑣1,𝑣2)}
UNION(𝑣1,𝑣2)
else
Remove edge
(𝑣1,𝑣2)
return A
B
C
F
D
E
4
A
6 3
2
4
2
5 1
Edges Weight
AB 4
BC 6
CD 3
DE 2
EF 4
AF 2
BF 5
CF 1
A ={ }

KRUSKAL(V,E)
:
A =
∅
foreach 𝑣∈V:
MAKE-SET(�
�
)
SET(𝑣2):
A = A ∪ {(𝑣1,𝑣2)}
UNION(𝑣1,𝑣2)
else
Remove edge
(𝑣1,𝑣2)
return
A
B
C
F
D
E
4
A
6 3
2
4
2
5 1
Edges Weight
AB 4
BC 6
CD 3
DE 2
EF 4
AF 2
BF 5
CF 1
A B C
A
={ }
F D
E

KRUSKAL(V,E)
:
A = ∅
foreach 𝑣 ∈ V:
MAKE-SET(𝑣)
SET(𝑣2):
A = A ∪ {(𝑣1,𝑣2)}
UNION(𝑣1,𝑣2)
else
Remove edge
(𝑣1,𝑣2)
return
A
B
C
F
D
E
4
A
6 3
2
4
2
5 1
Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
A B C
F D
E
A
={ }

KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
foreach ( 2)
𝑣1,𝑣 ∈
E:
if FIND-SET(𝑣1) ≠ FIND-
SET(𝑣2):
A = A ∪ {(𝑣1,𝑣2)}
UNION(𝑣1,𝑣2)
else
return A
B
C
F
D
E
4
A
6 3
2
4
2
5 1
A
={ }
A B C
F D
E
Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6

KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
E: if FIND-SET(�
�
1) ≠ FIND-SET(�
�
2
A = A ∪
{(𝑣1,𝑣2)}
UNION(𝑣1,𝑣2)
else
Remove edge
(𝑣1,𝑣2)
return
A
B
C
F
D
E
4
A
6 3
2
4
2
):
5 1
Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
A
={ }
A B C
F D
E

KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
SET(𝑣2): 2
A = A ∪ {(𝑣1,𝑣
)}
UNION(𝑣1,𝑣2)
else
Remove edge
(𝑣1,𝑣2)
return
A
B
C
F
D
E
4
A
6 3
2
4
2
5 1
Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
A ={(C,F)}
A B C
F D
E

KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
SET(𝑣2):
A = A ∪
{(𝑣1,𝑣2)}
UNION(𝑣1,
𝑣
2)
else
return
A
B
C
F
D
E
4
A
6 3
2
4
2
5 1
Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
A
={(C,F)}
A B
D
E
C,F

KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
E: if FIND-SET(�
�
1) ≠ FIND-SET(�
�
2
A = A ∪
{(𝑣1,𝑣2)}
UNION(𝑣1,𝑣2)
else
Remove edge
(𝑣1,𝑣2)
return
A
B
C
F
D
E
4
A
6 3
2
4
2
):
5 1
Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
A
={(C,F)}
A B
D
E
C,F

KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
SET(𝑣2): 2
A = A ∪ {(𝑣1,𝑣 )}
UNION(𝑣1,𝑣2)
else
Remove edge
(𝑣1,𝑣2)
return
A
B
F
D
E
4
A
6 3
2
4
2
5 1
Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
C
A ={(C,F),(A,F)}
A B
D
E
C,F

KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
SET(𝑣2):
A = A ∪
{(𝑣1,𝑣2)}
UNION(𝑣1,
𝑣
2)
else
return
A
B
F
D
E
4
A
6 3
2
4
2
5 1
A,C,F
Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
C
A ={(C,F),
(A,F)}
B
D
E

KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
E: if FIND-SET(�
�
1) ≠ FIND-SET(�
�
2
A = A ∪
{(𝑣1,𝑣2)}
UNION(𝑣1,𝑣2)
else
Remove edge
(𝑣1,𝑣2)
return
A
Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
B D
E
6 3
2
4
2
):
5 1
4
A
F
C
A ={(C,F),
(A,F)}
A,C,F
B
D
E

KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
SET(𝑣2): 2
A = A ∪ {(𝑣1,𝑣 )}
UNION(𝑣1,𝑣2)
else
Remove edge
(𝑣1,𝑣2)
return
A
Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
B
6 3
2
4
2
5 1
D
E
4
A
F
C
A ={(C,F),(A,F),(D,E)}
A,C,F
B
D
E

KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
SET(𝑣2):
A = A ∪
{(𝑣1,𝑣2)}
UNION(𝑣1,
𝑣
2)
else
return
A
Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
D,E
B
6 3
2
4
2
5 1
D
E
4
A
F
C
A ={(C,F),(A,F),
(D,E)}
A,C,F
B

KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
E: if FIND-SET(�
�
1) ≠ FIND-SET(�
�
2
A = A ∪
{(𝑣1,𝑣2)}
UNION(𝑣1,𝑣2)
else
Remove edge
(𝑣1,𝑣2)
return
A
Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
B
6 3
2
4
2
):
5 1
4
A
C
F
D
E
A ={(C,F),(A,F),
(D,E)}
D,E
A,C,F
B

KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
SET(𝑣2): 2
A = A ∪ {(𝑣1,𝑣 )}
UNION(𝑣1,𝑣2
)
else
Remove edge
(𝑣1,𝑣2)
return
A
Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
B
6 3
2
4
2
5 1
4
A
C
F
D
E
A ={(C,F),(A,F),(D,E),
(C,D)}
D,E
A,C,F
B

KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
SET(𝑣2):
A = A ∪
{(𝑣1,𝑣2)}
UNION(𝑣1,
𝑣
2)
else
Remove edge
(𝑣1,𝑣2)
return
A
Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
A,C,D,E,F
B
6 3
2
4
2
5 1
4
A
C
F
D
E
A ={(C,F),(A,F),
(D,E), (C,D)}
B

KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
E: if FIND-SET(�
�
1) ≠ FIND-SET(�
�
2
A = A ∪
{(𝑣1,𝑣2)}
UNION(𝑣1,𝑣2
)
else
Remove edge
(𝑣1,𝑣2)
return
A
Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
B
6 3
2
4
2
):
5 1
4
A
C
F
D
E
A ={(C,F),(A,F),
(D,E), (C,D)}
A,C,D,E,F
B

KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
SET(𝑣2): 2
A = A ∪ {(𝑣1,𝑣 )}
UNION(𝑣1,𝑣2
)
else
Remove edge
(𝑣1,𝑣2)
return
A
Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
6 3
2
4
2
5 1
B
4
A
C
F
D
E
A ={(C,F),(A,F),(D,E),
(C,D),(A,B)}
A,C,D,E,F
B

Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
B
C
F
D
E
4
A
6 3
2
4
2
5 1
KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
SET(𝑣2):
A = A ∪
{(𝑣1,𝑣2)}
UNION(𝑣1,
𝑣
2)
else
Remove edge
(𝑣1,𝑣2)
return A
A ={(C,F),(A,F),
(D,E), (C,D),
(A,B)}
A,B,C,D,E,F

Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
6 3
2
4
5 1
4
A
B
C
F
D
E
KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
E: if FIND-SET(�
�
1) ≠ FIND-SET(�
�
2
2
):
A = A ∪
{(𝑣1,𝑣2)}
UNION(𝑣1,𝑣2
)
else
Remove edge
(𝑣1,𝑣2)
return A
A ={(C,F),(A,F),
(D,E), (C,D),
(A,B)}
A,B,C,D,E,F

Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
F
E
6 3
2
4
2
5 1
Is in a same set.
4
A
B
C
D
It is cyclic
KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
SET(𝑣2):
A = A ∪ {(𝑣1,𝑣2)}
UNION(𝑣1,𝑣2
)
else
Remove edge
(𝑣1,𝑣2)
return A
A ={(C,F),(A,F),
(D,E), (C,D),
(A,B)}
A,B,C,D,E,F

Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
B
C
F
D
E
4
A
6 3
2
2
5 1
KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
SET(𝑣2):
A = A ∪ {(𝑣1,𝑣2)}
UNION(𝑣1,𝑣2)
else
Remove edge
(
𝑣1,
𝑣
2)
return
A
A ={(C,F),(A,F),
(D,E), (C,D),
(A,B)}
A,B,C,D,E,F
4

Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
6 3
2
5 1
F
E
4
A
B
C
D
KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
E: if FIND-SET(�
�
1) ≠ FIND-SET(�
�
2
2
):
A = A ∪
{(𝑣1,𝑣2)}
UNION(𝑣1,𝑣2
)
else
Remove edge
(𝑣1,𝑣2)
return A
A ={(C,F),(A,F),
(D,E), (C,D),
(A,B)}
A,B,C,D,E,F

KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
SET(𝑣2):
A = A ∪ {(𝑣1,𝑣2)}
UNION(𝑣1,𝑣2
)
else
Remove edge
(𝑣1,𝑣2)
return A
Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
B
C
F
D
E
4
A
6 3
2
2
5 1
Is in a same set.
It is cyclic
A ={(C,F),(A,F),
(D,E), (C,D),
(A,B)}
A,B,C,D,E,F

Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
B
C
F
D
E
4
A
6 3
2
2
1
KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
SET(𝑣2):
A = A ∪ {(𝑣1,𝑣2)}
UNION(𝑣1,𝑣2)
else
Remove edge
(
𝑣1,
𝑣
2)
return
A
A ={(C,F),(A,F),
(D,E), (C,D),
(A,B)}
A,B,C,D,E,F
5

Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
6 3
2
1
F
E
4
A
B
C
D
KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
E: if FIND-SET(�
�
1) ≠ FIND-SET(�
�
2
2
):
A = A ∪
{(𝑣1,𝑣2)}
UNION(𝑣1,𝑣2
)
else
Remove edge
(𝑣1,𝑣2)
return A
A ={(C,F),(A,F),
(D,E), (C,D),
(A,B)}
A,B,C,D,E,F

KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
SET(𝑣2):
A = A ∪ {(𝑣1,𝑣2)}
UNION(𝑣1,𝑣2
)
else
Remove edge
(𝑣1,𝑣2)
return A
Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
B
C
F
D
E
4
A
6 3
2
2
1
It is cyclic
A ={(C,F),(A,F),
(D,E), (C,D),
(A,B)}
Is in a same set.
A,B,C,D,E,F

Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
B
C
F
D
E
4
A
3
2
2
1
KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
SET(𝑣2):
A = A ∪ {(𝑣1,𝑣2)}
UNION(𝑣1,𝑣2)
else
Remove edge
(
𝑣1,
𝑣
2)
return
A
A ={(C,F),(A,F),
(D,E), (C,D),
(A,B)}
A,B,C,D,E,F
6

Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
3
2
2
1
F
E
4
A
B
C
D
KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
SET(𝑣2):
A = A ∪ {(𝑣1,𝑣2)}
UNION(𝑣1,𝑣2)
else
Remove edge
(𝑣1,𝑣2)
return A
A ={(C,F),(A,F),(D,E),
(C,D),(A,B)}

KRUSKAL(V,E)
:
A = ∅
SET(𝑣)
E: if FIND-SET(𝑣1) ≠ FIND-SET(𝑣2):
A = A ∪ {(𝑣1,𝑣2)}
UNION(𝑣1,𝑣2)
else
return A
Edges Weight
CF 1
AF 2
DE 2
CD 3
AB 4
FE 4
BF 5
BC 6
3
2
2
1
F
E
4
A
B
C
D
A ={(C,F),(A,F),(D,E),(C,D),
(A,B)}
Total Weight :- 1 + 2 +
2 + 3 + 4

KRUSKAL(V,E)
:
A = ∅
foreach 𝑣 ∈ V: MAKE-SET(𝑣)
A = A ∪ {(𝑣1,𝑣2)} UNION(𝑣1,𝑣2)
else
return A
Time
Complexity
O(1)
O(V)
O(E log E)
O(E log V)

KRUSKAL(V,E)
:
Time
Complexity
O(1)
O(V)
O(E log E)
A = ∅
foreach 𝑣 ∈ V: MAKE-SET(𝑣)
A = A ∪ {(𝑣1,𝑣2)} UNION(𝑣1,𝑣2)
else
return A
Time Complexity = O(1)+ O(V)+O(E log E)+O(E log V)
= O(E log E) + O(E log V) Since, |E| ≤ |V|2 ⇒log |E| = O(2 log V) = O(log V).
= O(E log V) + O(E log V)
= O(E log V)
O(E log V)

Real-life applications of Kruskal's
algorithm
• Landing Cables
• TV Network
• Tour Operations
• Computer networking
• Study of Molecular bonds in Chemistry
• Routing Algorithms

Problem: Laying Telephone
Wire
Central office

Wiring: Naïve
Approach
Central office
Expensive!

Wiring: Better
Approach
Central office
Minimize the total length of wire connecting the customers

EXAMPLE:-
A cable company want to connect five villages to their network which currently extends to
the market town of Avonford. What is the minimum length of cable needed?

All vertices have been
connected.
The solution is
ED 2
AB 3
CD 4
AE 4
EF 5
Total weight of tree:
18
A
B C
D
2
7
4
F
5
8
4
5
3
6
8
Solution
E

kruskal Algorithm in Algorithm for CS St

More Related Content

Similar to kruskal Algorithm in Algorithm for CS St

Recently uploaded

kruskal Algorithm in Algorithm for CS St