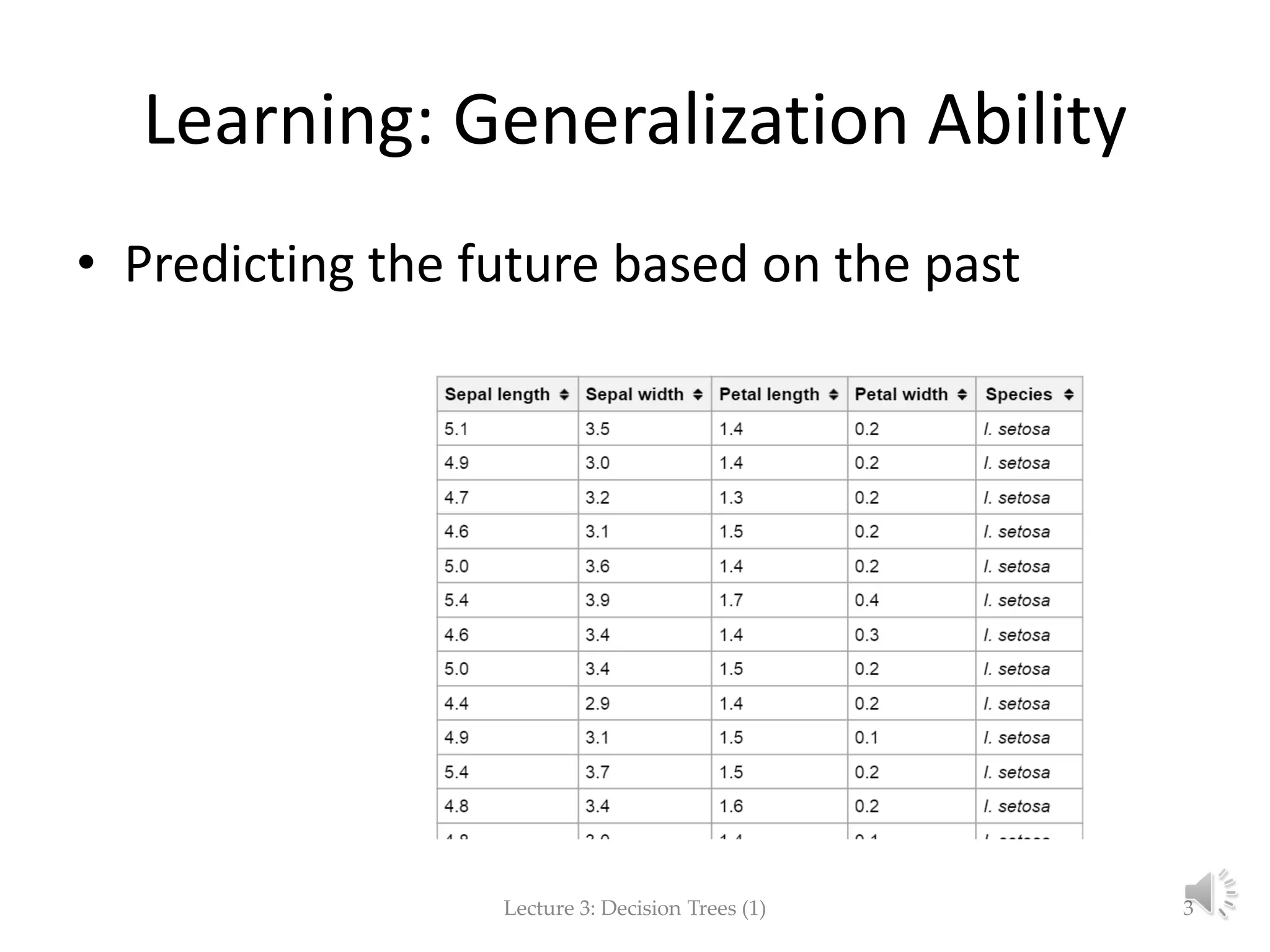
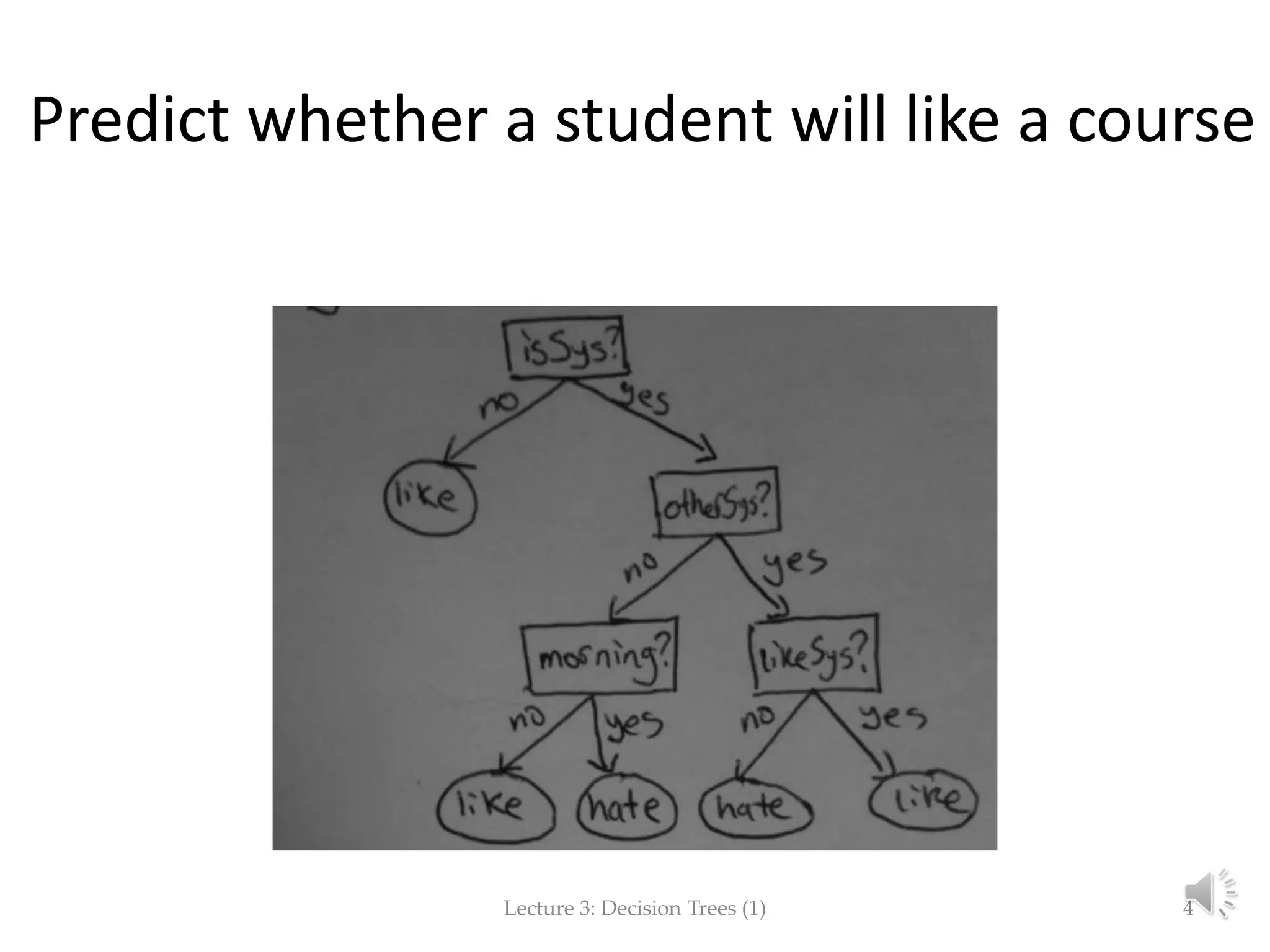
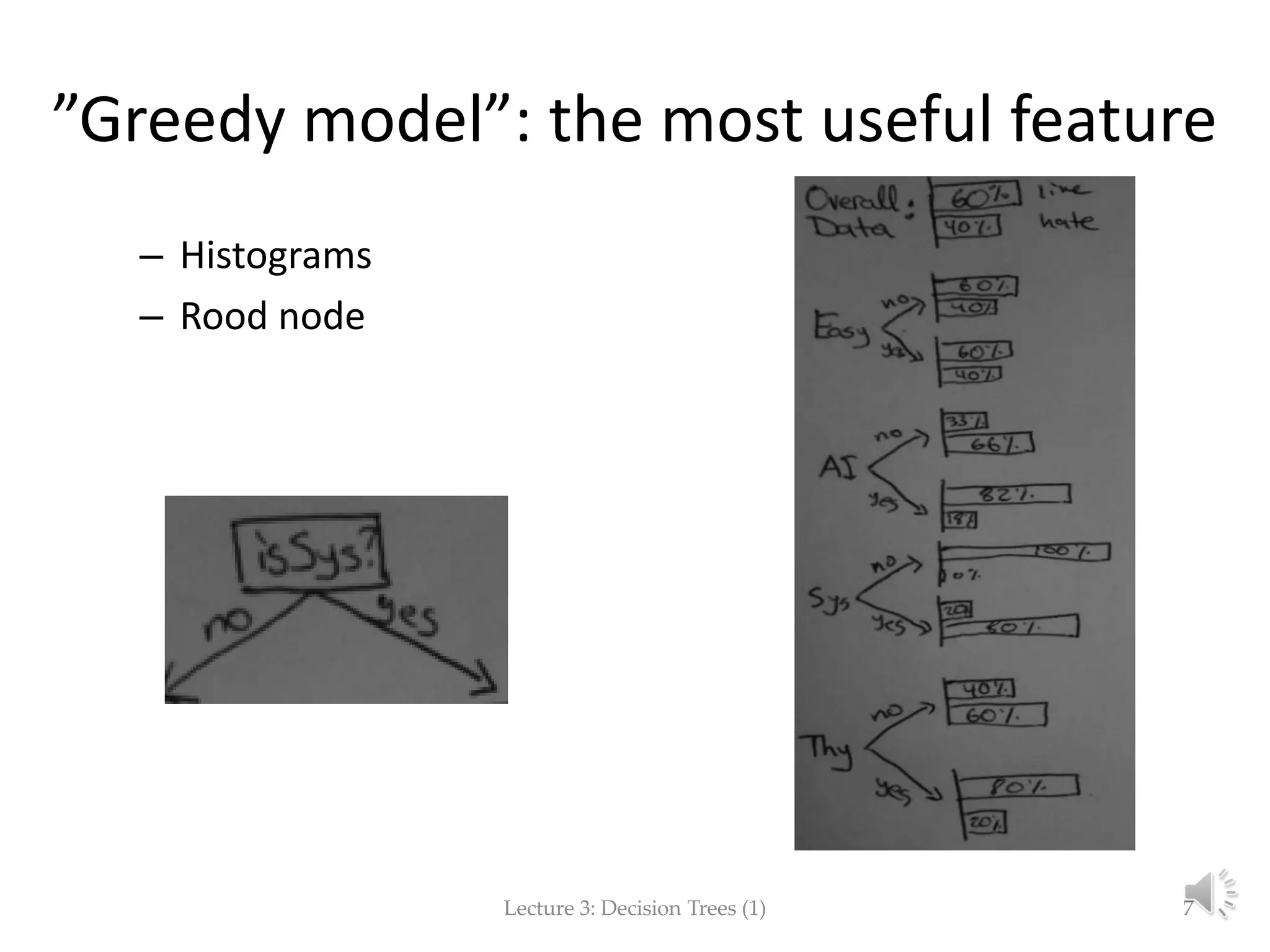
The document focuses on decision trees in machine learning, outlining concepts such as greedy models, divide and conquer strategies, inductive bias, loss functions, and expected loss. It explains the structure of decision trees, which consist of nodes representing tests on attributes and class labels, and discusses the importance of training and empirical errors in learning. The content is framed within a lecture series by Marina Santini at Uppsala University in 2015.