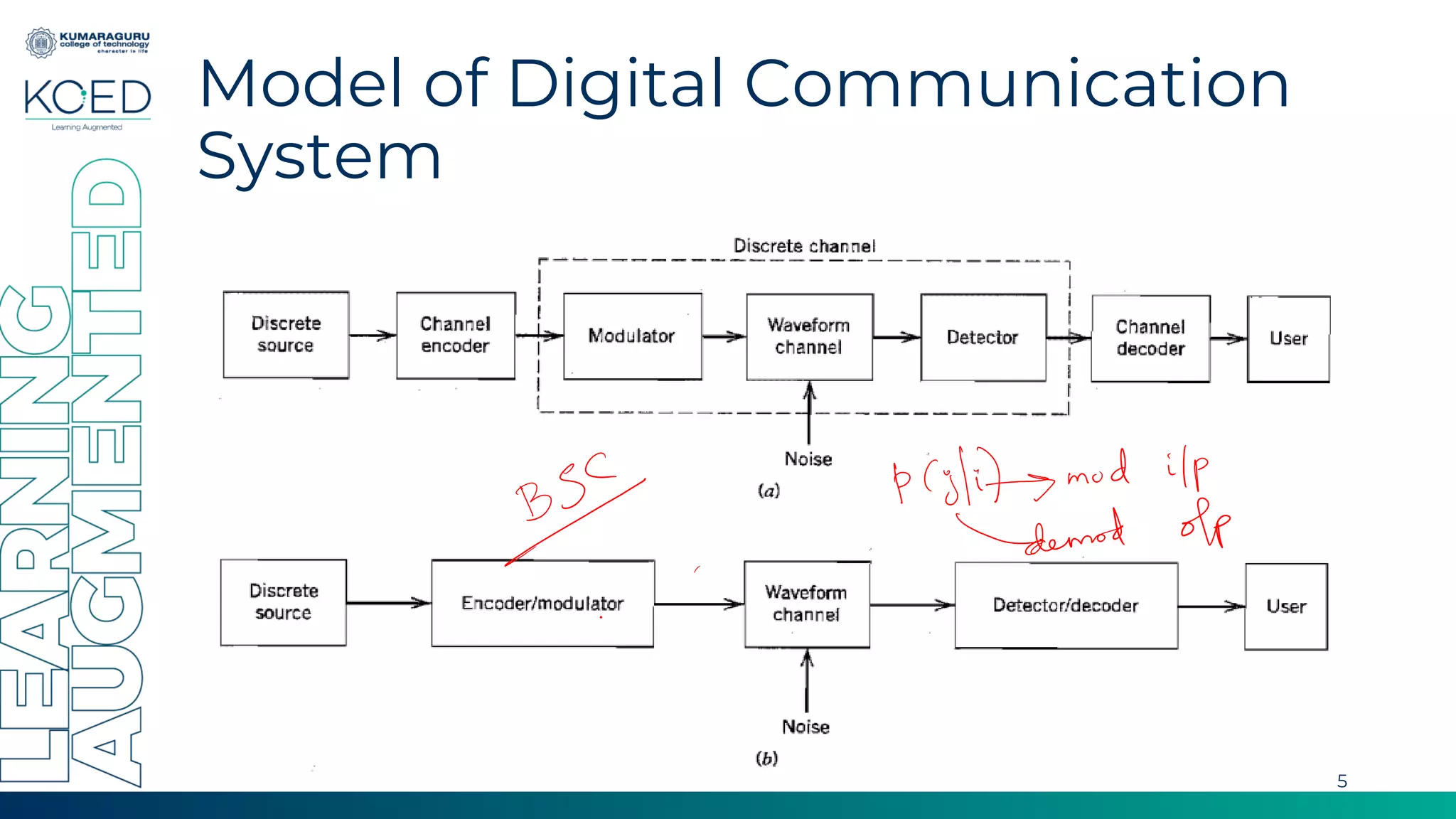
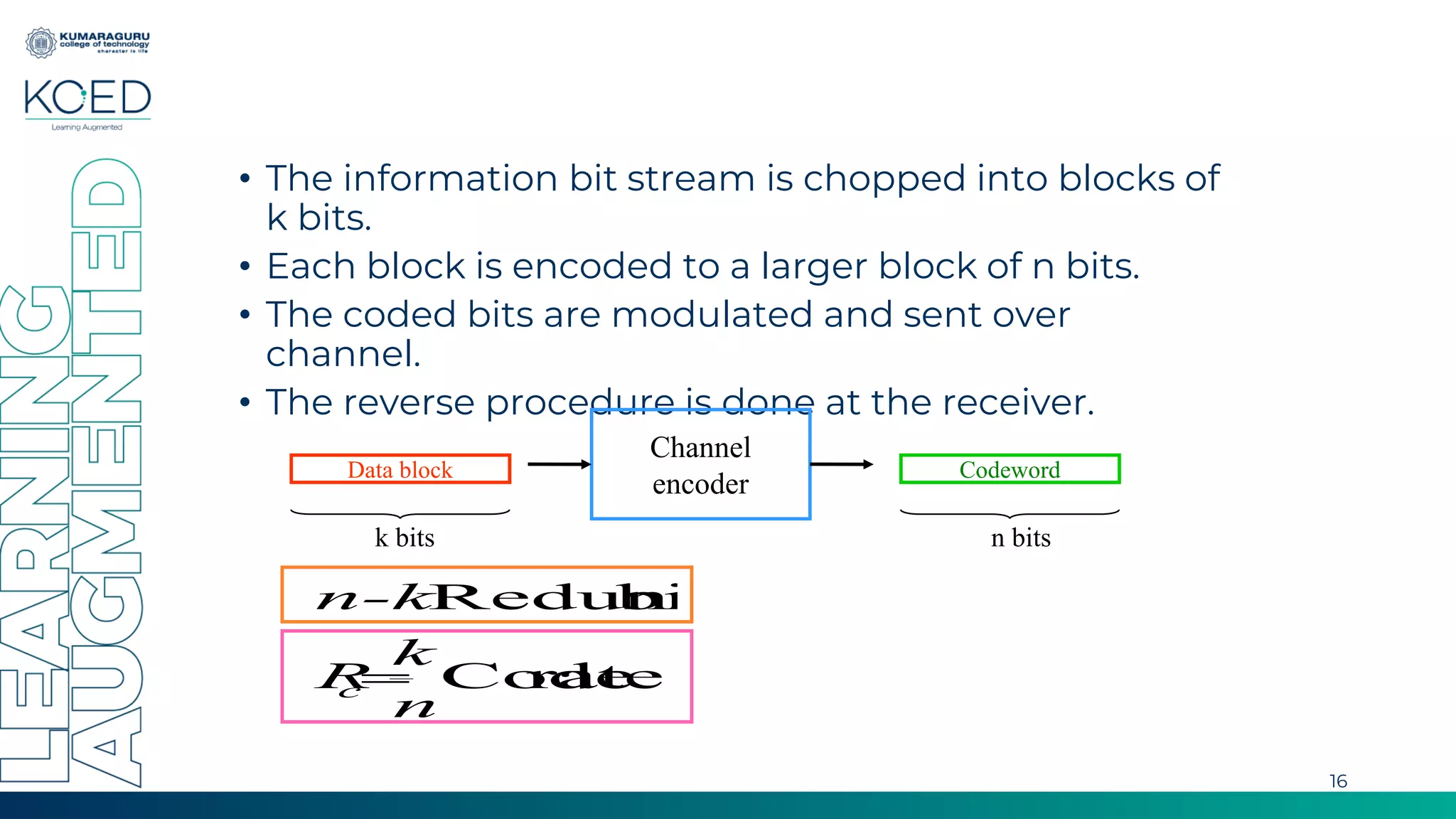
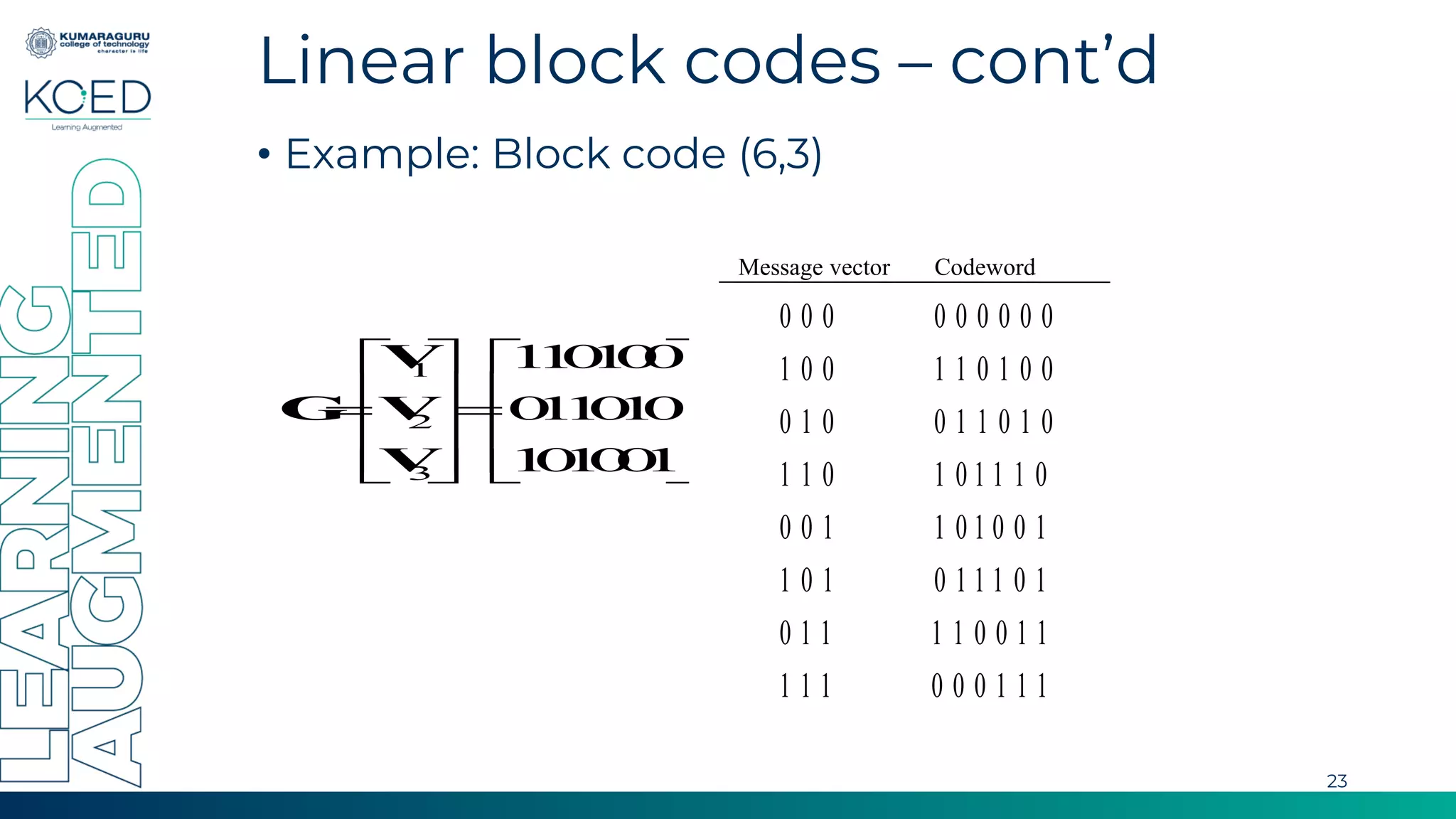
Linear block codes take binary data in blocks and encode them into longer codewords by adding redundant bits to allow for error detection and correction. The document discusses key concepts of linear block codes including generator and parity check matrices, syndrome detection, minimum distance, and applications. It also provides an example of a (6,3) linear block code and a (7,4) Hamming code.







![Linear block codes
• A code is said to be linear if any two code words in the
code can be added in modulo-2 arithmetic to produce
a third code word in the code.
• (n,k) representation
• n-o/p bits; k-msg bits[ 2^k msg combinations]
• n-k—parity bits
• Code word structure:
9](https://image.slidesharecdn.com/linearblockcode-230802060126-dff993a2/75/Linear-Block-code-pdf-9-2048.jpg)









![Linear block codes – cont’d
• Systematic block code (n,k)
• For a systematic code, the first (or last) k elements
in the codeword are information bits.
matrix
)
(
matrix
identity
]
[
k
n
k
k
k
k
k
k
−
=
=
=
P
I
I
P
G
)
,...,
,
,
,...,
,
(
)
,...,
,
(
bits
message
2
1
bits
parity
2
1
2
1
k
k
n
n m
m
m
p
p
p
u
u
u −
=
=
U
20](https://image.slidesharecdn.com/linearblockcode-230802060126-dff993a2/75/Linear-Block-code-pdf-20-2048.jpg)
![Linear block codes – cont’d
• Systematic block code (n,k)
• For a systematic code, the first (or last) k elements
in the codeword are information bits.
matrix
)
(
matrix
identity
]
[
k
n
k
k
k
k
k
k
−
=
=
=
P
I
I
P
G
)
,...,
,
,
,...,
,
(
)
,...,
,
(
bits
message
2
1
bits
parity
2
1
2
1
k
k
n
n m
m
m
p
p
p
u
u
u −
=
=
U
21](https://image.slidesharecdn.com/linearblockcode-230802060126-dff993a2/75/Linear-Block-code-pdf-21-2048.jpg)

![Linear block codes – cont’d
• For any linear code we can find an matrix
such that its rows are orthogonal to the
rows of :
• H is called the parity check matrix and
its rows are linearly independent.
• For systematic linear block codes:
n
k
n
− )
(
H
G
0
GH =
T
]
[ T
k
n P
I
H −
=
24](https://image.slidesharecdn.com/linearblockcode-230802060126-dff993a2/75/Linear-Block-code-pdf-24-2048.jpg)







![PROPERTY 3:
• The syndrome s is the sum of those columns of
matrix H corresponding to the error locations
H=[ …… ]therefore,
s=
32](https://image.slidesharecdn.com/linearblockcode-230802060126-dff993a2/75/Linear-Block-code-pdf-32-2048.jpg)






![Hamming codes
• Example: Systematic Hamming code
(7,4)
]
[
1
0
1
1
1
0
0
1
1
0
1
0
1
0
1
1
1
0
0
0
1
3
3
T
P
I
H
=
=
]
[
1
0
0
0
1
1
1
0
1
0
0
0
1
1
0
0
1
0
1
0
1
0
0
0
1
1
1
0
4
4
=
= I
P
G
39](https://image.slidesharecdn.com/linearblockcode-230802060126-dff993a2/75/Linear-Block-code-pdf-39-2048.jpg)







