Numpy_Arrays in python libraries use.pptx

Numpy_Arrays in python libraries use.pptx

• 1.
  NumPy Arrays inDetail With Examples and Output
• 2.
  What is NumPy? •NumPy (Numerical Python) is a library for numerical operations. • - Supports multi-dimensional arrays • - Efficient and fast operations • - Used in ML, data science, and scientific computing
• 3.
  Creating Arrays • 1DArray: np.array([1, 2, 3]) → [1 2 3] • 2D Array: np.array([[1, 2], [3, 4]]) → [[1 2] [3 4]]
• 4.
  Array Attributes • a.shape→ (2, 2) • a.ndim → 2 • a.dtype → int64 • a.itemsize → 8
• 5.
  Array Creation Functions •np.zeros((2,2)) → [[0. 0.] [0. 0.]] • np.ones((2,2)) → [[1. 1.] [1. 1.]
• 6.
  Array Range andLinspace • np.arange(0, 10, 2) → [0 2 4 6 8] • np.linspace(0, 1, 5) → [0. 0.25 0.5 0.75 1. ]
• 7.
  Random Arrays • np.random.rand(2,2)→ 2x2 array with random floats [0,1) • np.random.randint(1, 10, (2, 2)) → 2x2 array of ints
• 8.
  Indexing and Slicing •a = np.array([[1, 2], [3, 4]]) • a[0,1] → 2 • a[:,0] → [1 3] • a[1,:] → [3 4]
• 9.
  Reshaping and Flattening •a = np.arange(6).reshape(2, 3) → [[0 1 2] • [3 4 5]] • a.flatten() → [0 1 2 3 4 5]
• 10.
  Mathematical Operations • a= np.array([1, 2, 3]) • b = np.array([4, 5, 6]) • a + b → [5 7 9] • a * b → [4 10 18] • np.sqrt(a) → [1. 1.41 1.73]
• 11.
  Aggregate Functions • a= np.array([[1, 2], [3, 4]]) • a.sum() → 10 • a.mean() → 2.5 • a.min() → 1 • a.max() → 4 • a.sum(axis=0) → [4 6]
• 12.
  Broadcasting • a =np.array([[1], [2], [3]]) • b = np.array([10, 20]) • a + b → [[11 21] • [12 22] • [13 23]]
• 13.
  Copy vs View •a = np.array([1, 2, 3]) • b = a.view() → Shares memory • c = a.copy() → New memory • Changing b affects a; changing c does not
• 14.
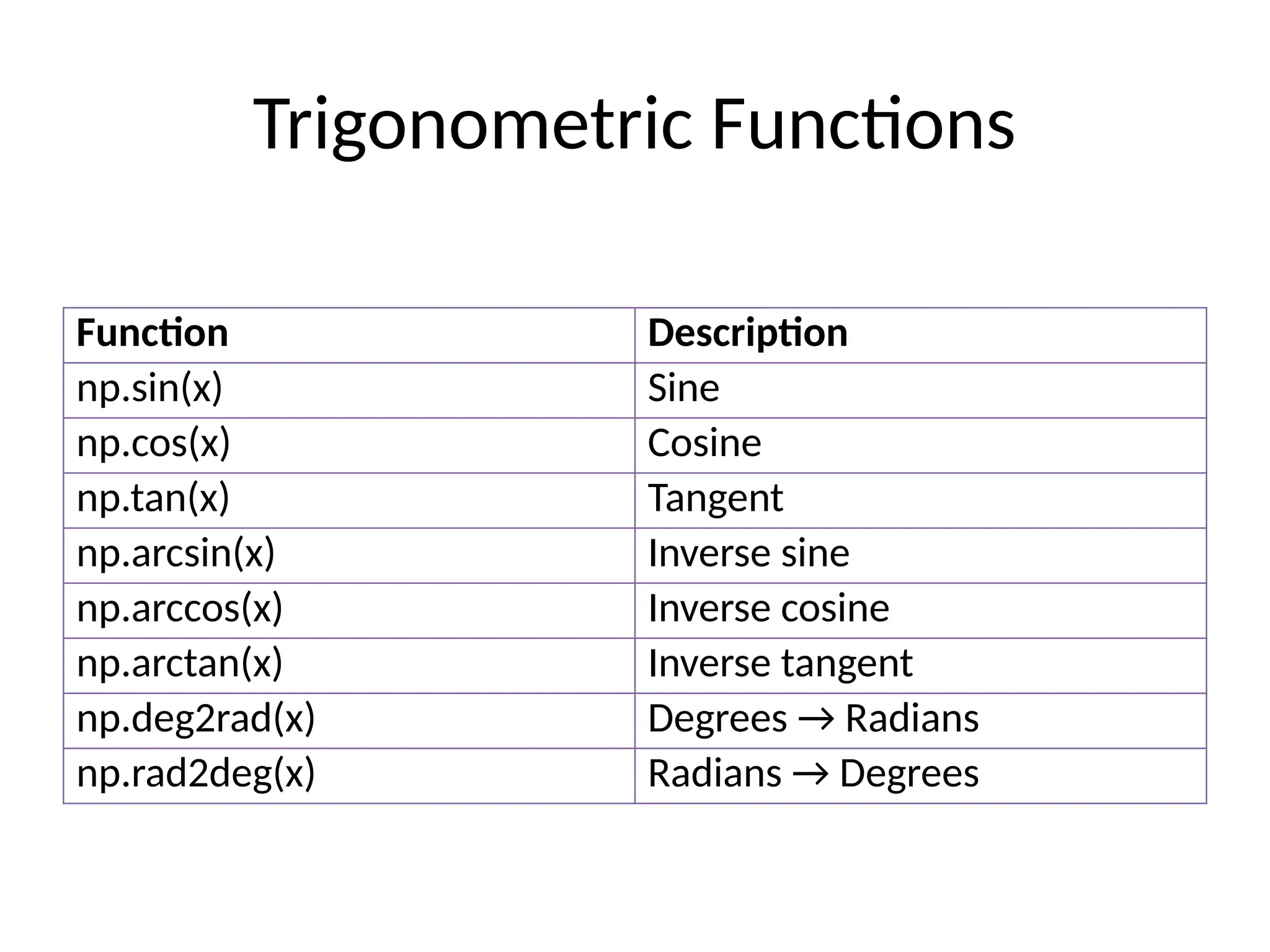
  Trigonometric Functions Function Description np.sin(x)Sine np.cos(x) Cosine np.tan(x) Tangent np.arcsin(x) Inverse sine np.arccos(x) Inverse cosine np.arctan(x) Inverse tangent np.deg2rad(x) Degrees → Radians np.rad2deg(x) Radians → Degrees
• 15.
  Example import numpy asnp angle_deg = 45 angle_rad = np.deg2rad(angle_deg) print("sin(45°):", np.sin(angle_rad)) print("cos(45°):", np.cos(angle_rad)) print("tan(45°):", np.tan(angle_rad))
• 16.
  Exponential Functions Function Description np.exp(x)exe^x np.exp2(x) 2x2^x np.expm1(x) ex−1e^x - 1 (more accurate for small x)
• 17.
  Example x = 3 print("e^3:",np.exp(x)) print("2^3:", np.exp2(x)) print("exp(3) - 1:", np.expm1(x))
• 18.
  Logarithmic Functions Function Description np.log(x)Natural log ln⁡ xln x np.log10(x) Base-10 log np.log2(x) Base-2 log np.log1p(x) ln⁡ (1+x) (accurate for small x)
• 19.
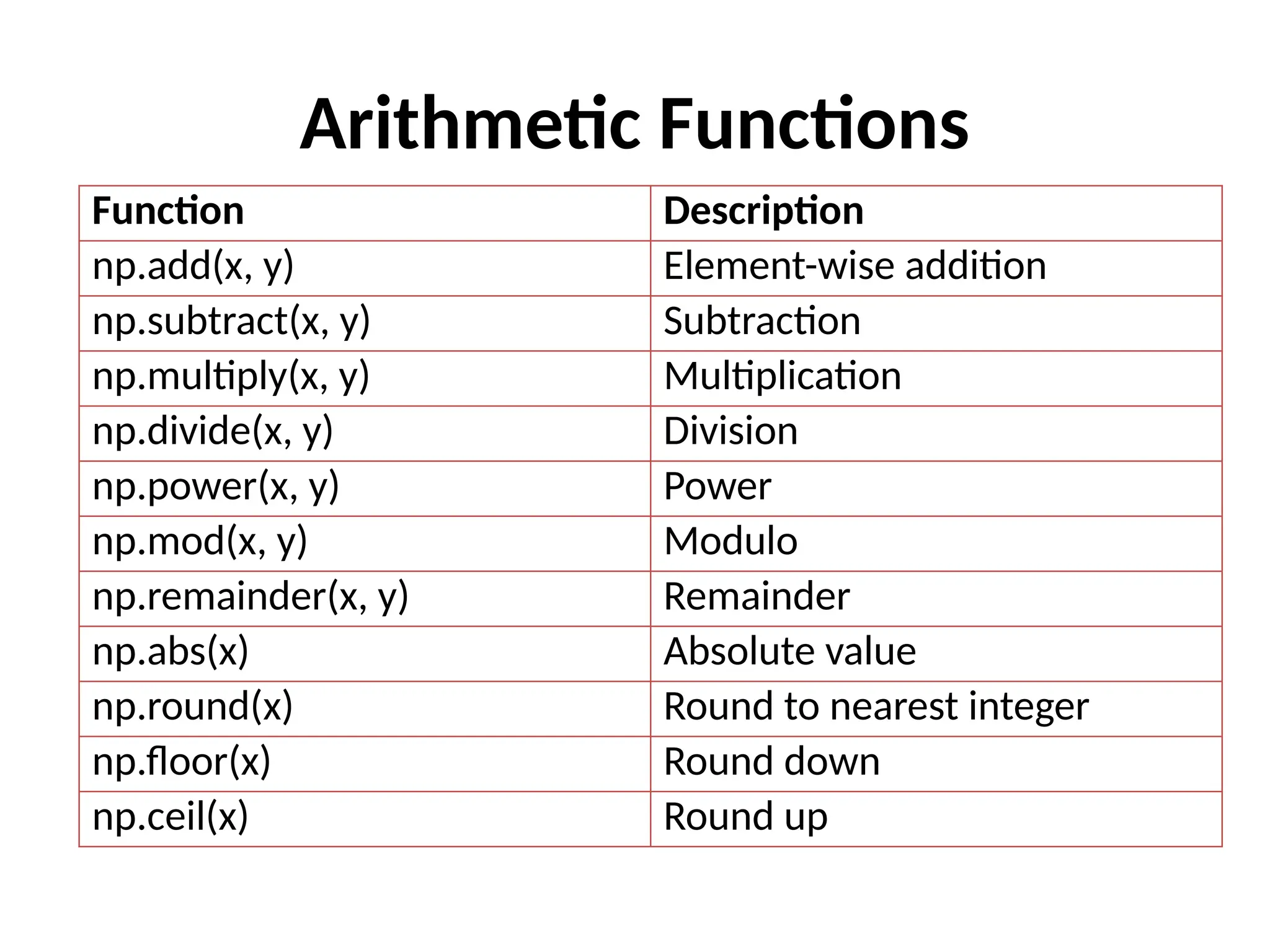
  Example x = 10 print("log(x):",np.log(x)) print("log10(x):", np.log10(x)) print("log2(x):", np.log2(x)) print("log1p(x):", np.log1p(x))
• 20.
  Arithmetic Functions Function Description np.add(x,y) Element-wise addition np.subtract(x, y) Subtraction np.multiply(x, y) Multiplication np.divide(x, y) Division np.power(x, y) Power np.mod(x, y) Modulo np.remainder(x, y) Remainder np.abs(x) Absolute value np.round(x) Round to nearest integer np.floor(x) Round down np.ceil(x) Round up
• 21.
  Example a = np.array([1,2, 3]) b = np.array([4, 5, 6]) print("a + b:", np.add(a, b)) print("a * b:", np.multiply(a, b)) print("a^2:", np.power(a, 2)) print("abs([-3, -5]):", np.abs([-3, -5]))