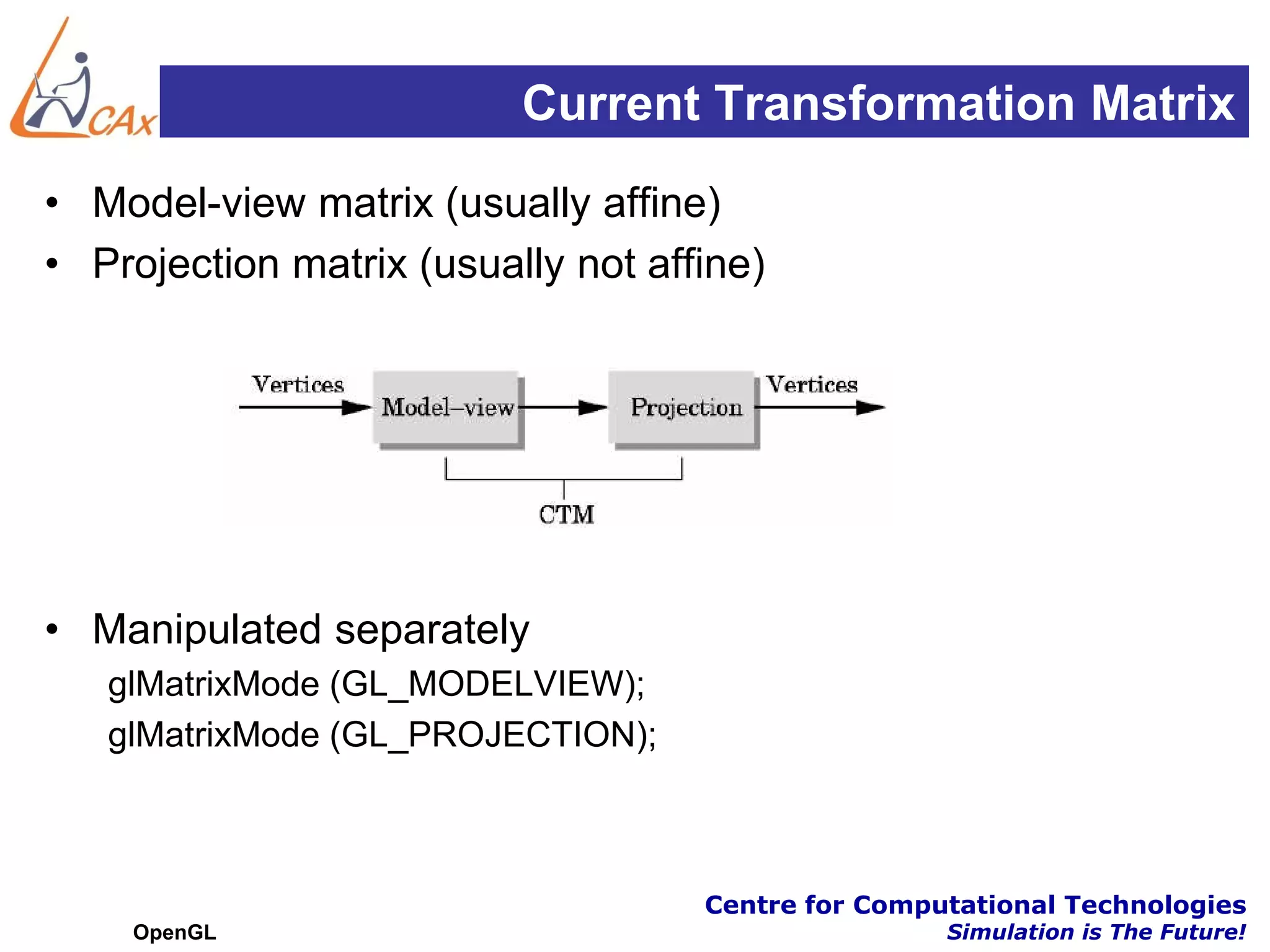
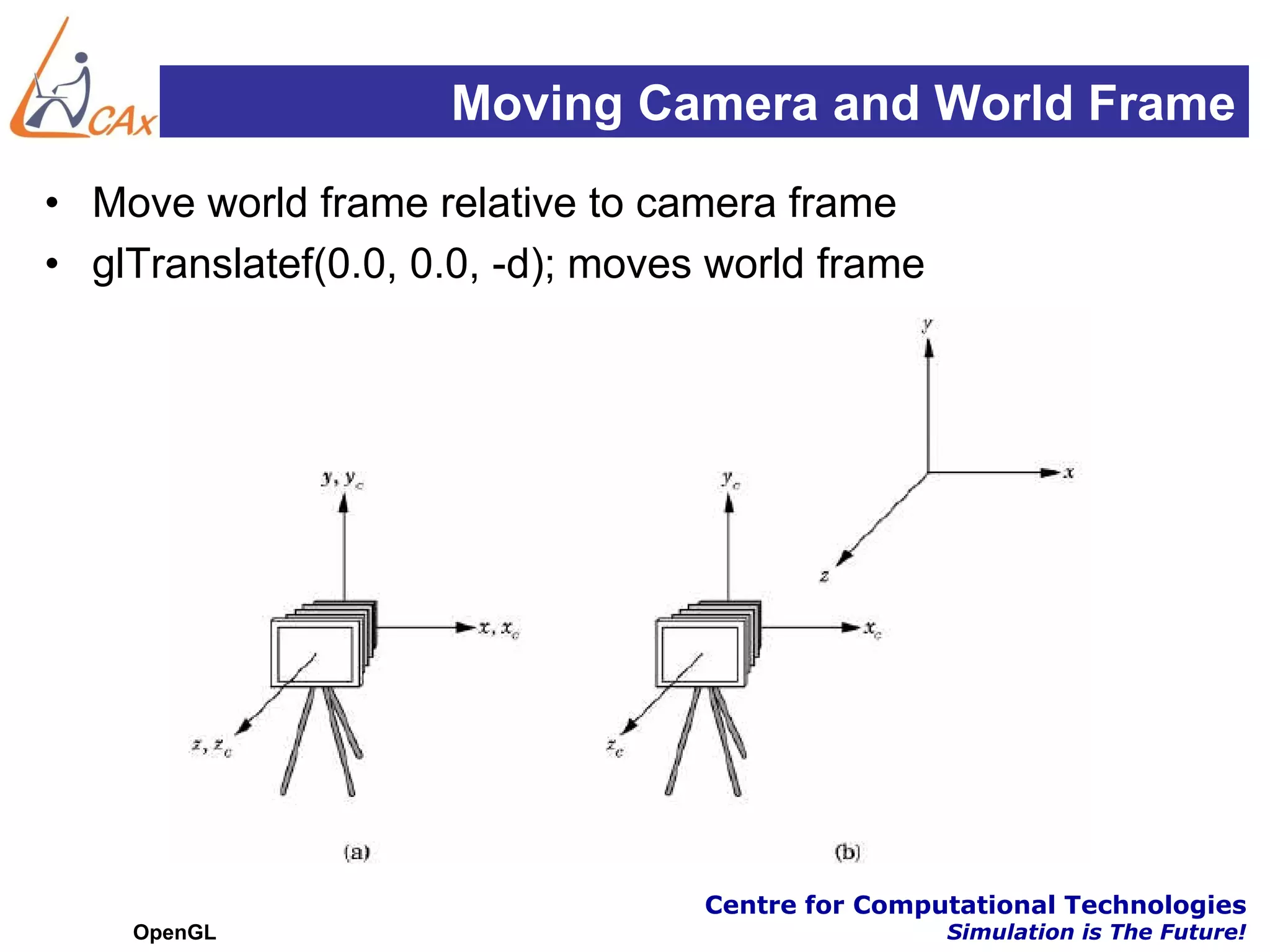
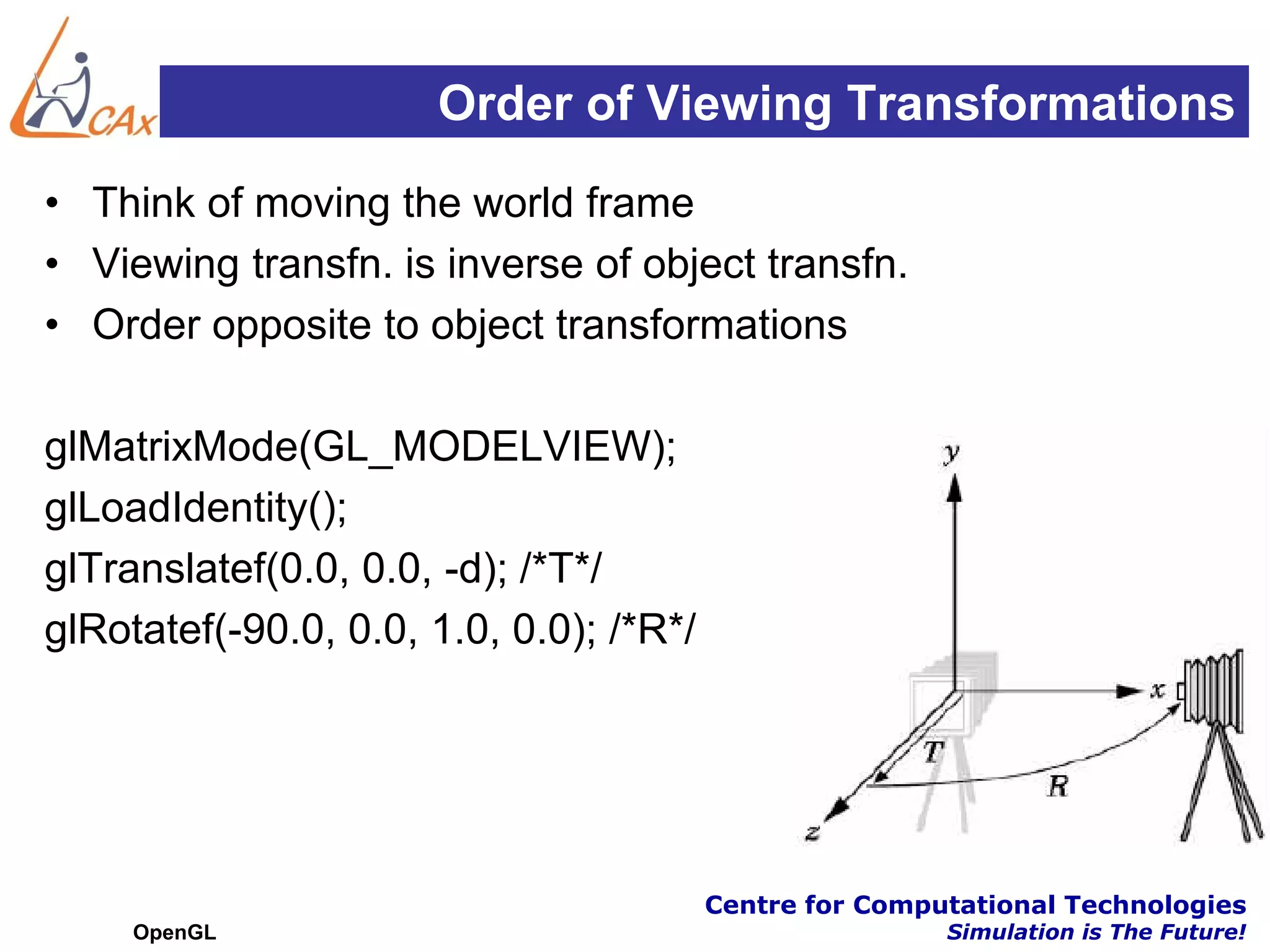
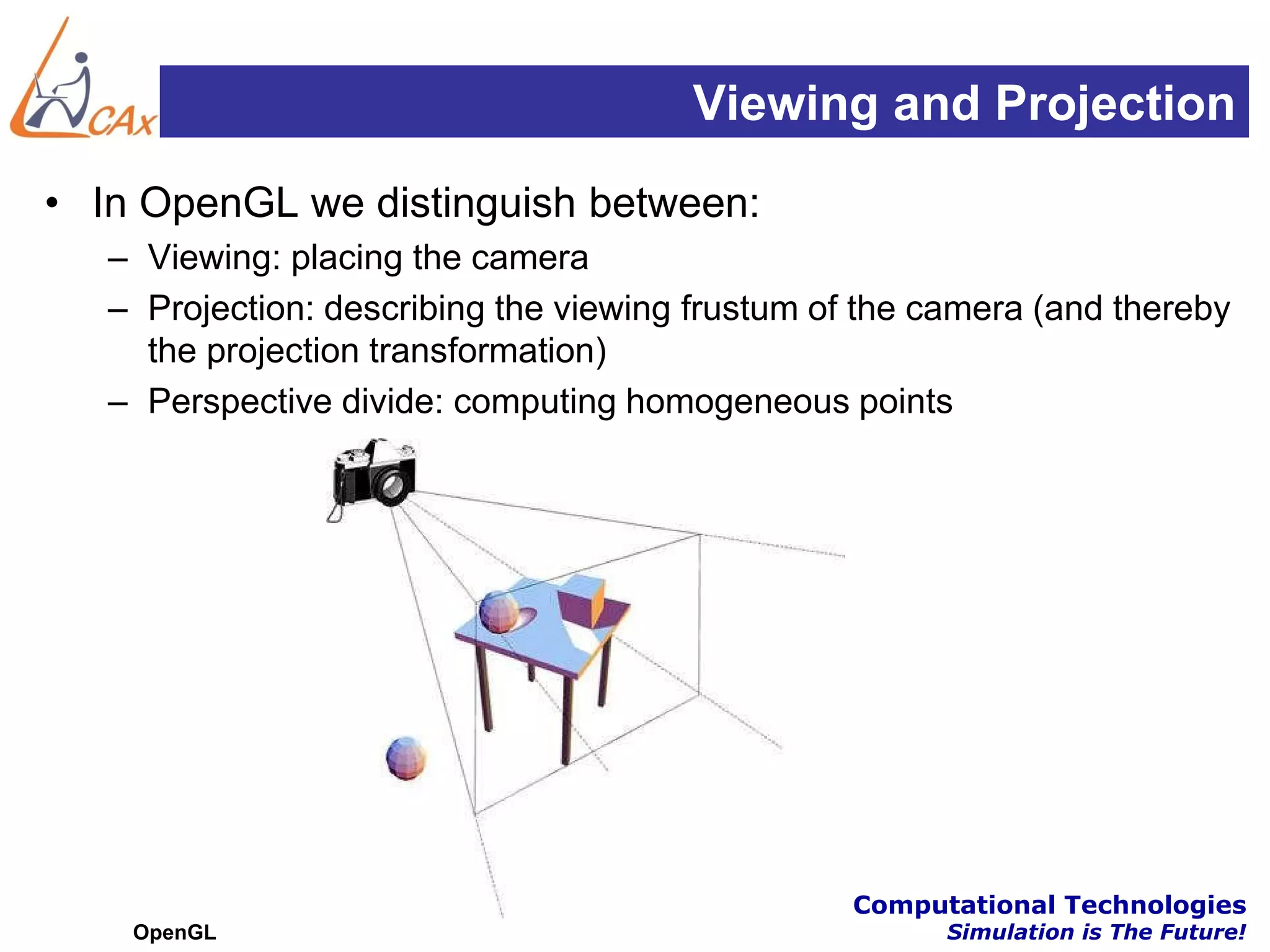
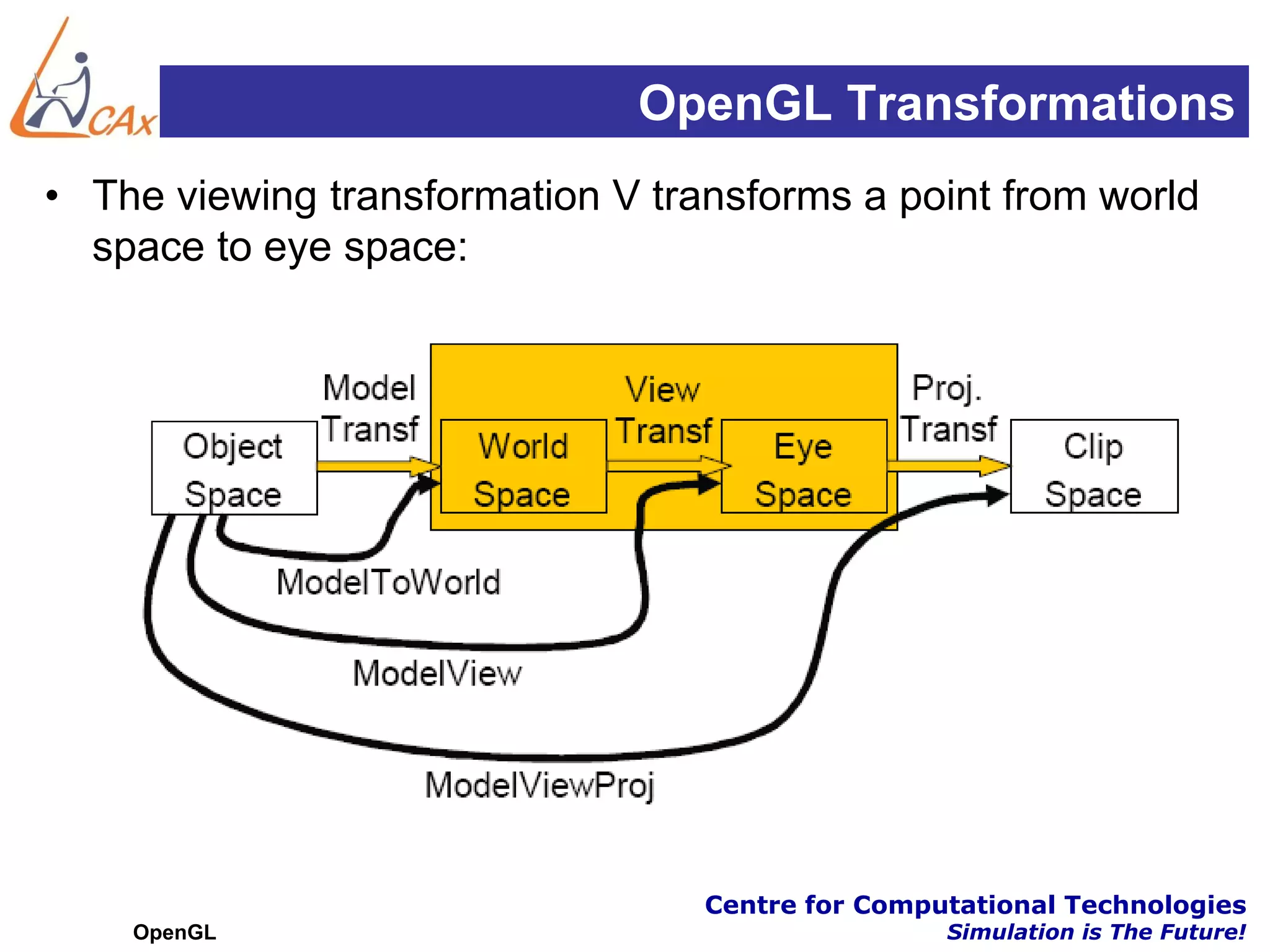
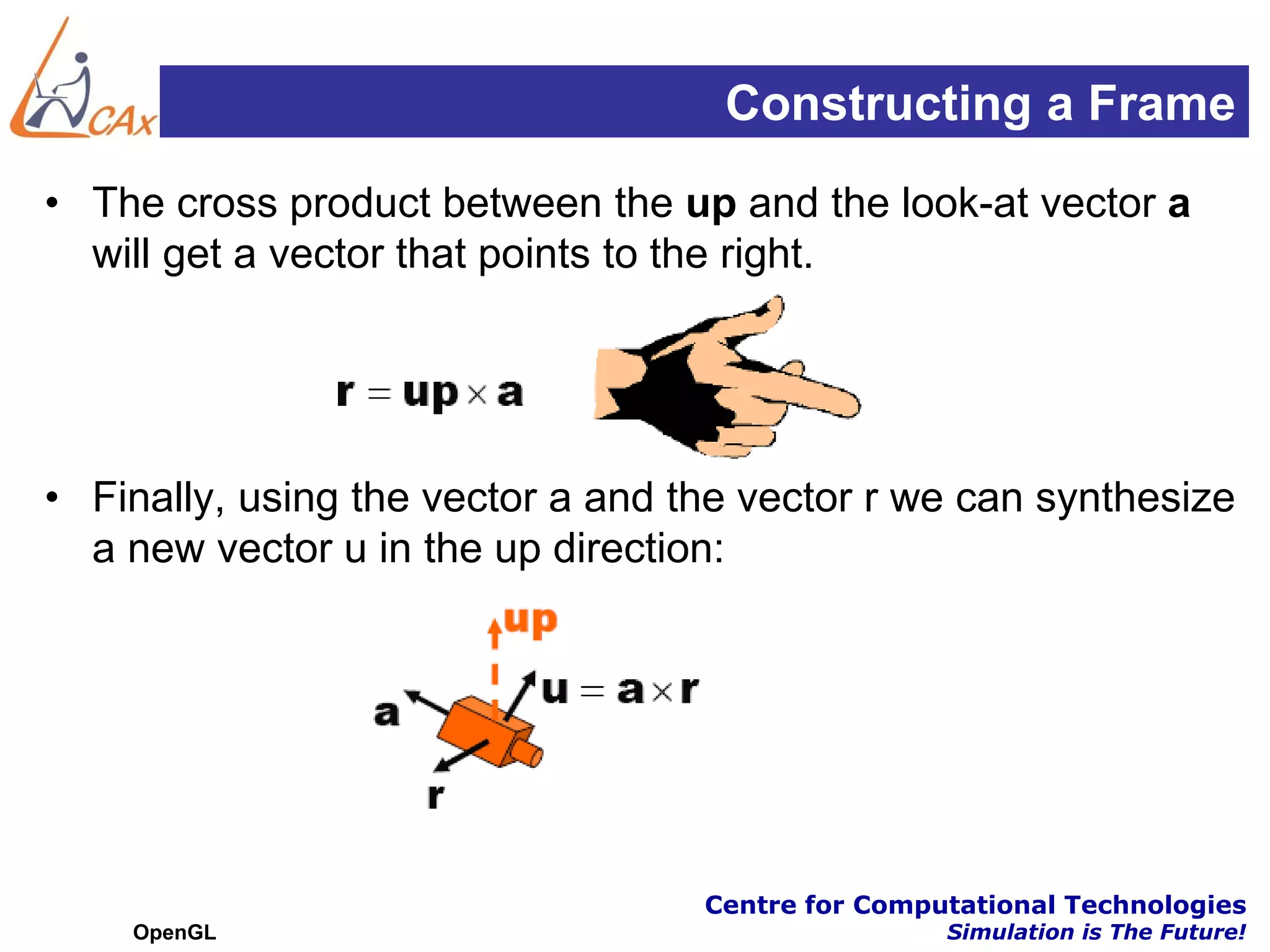
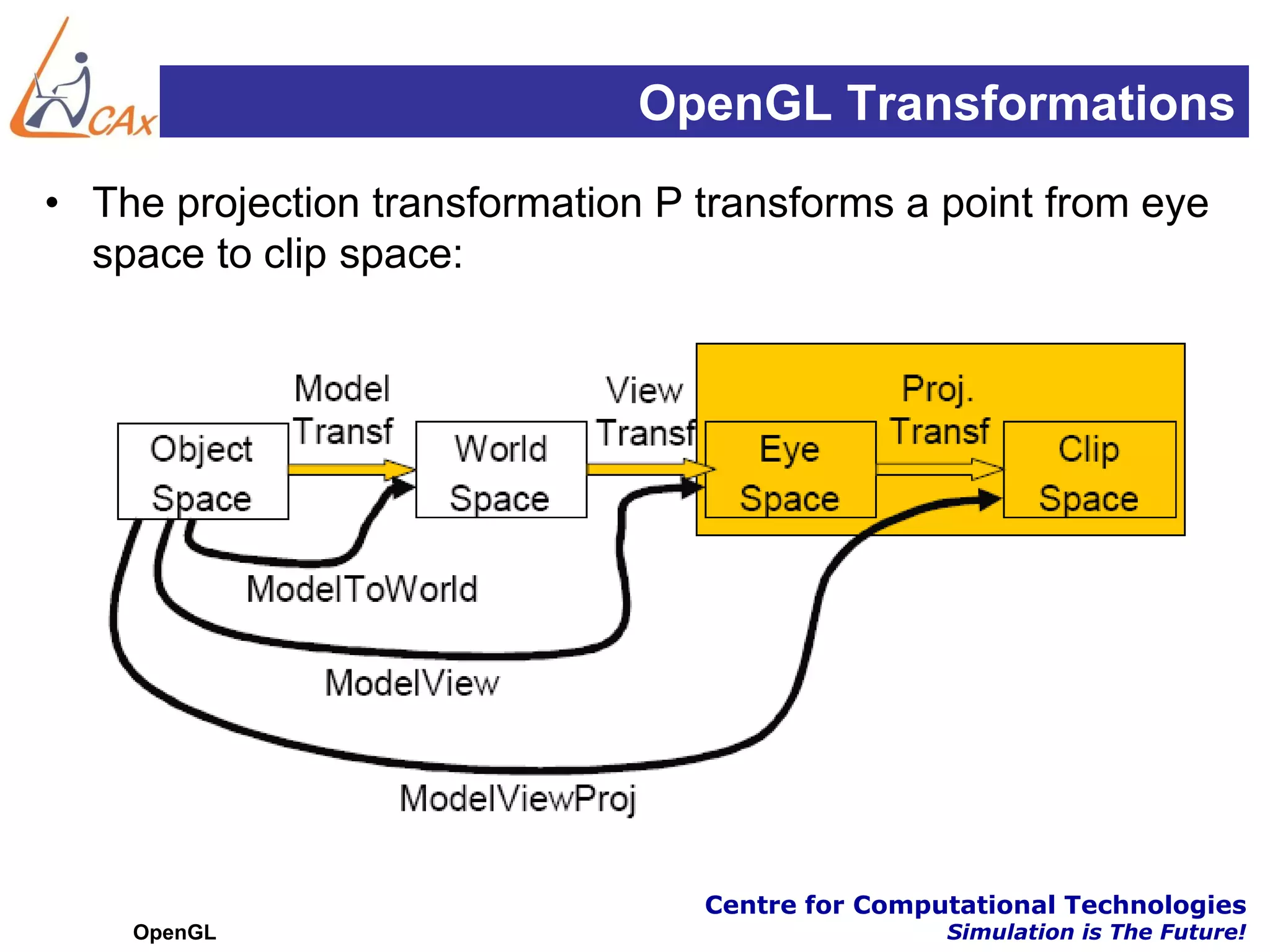
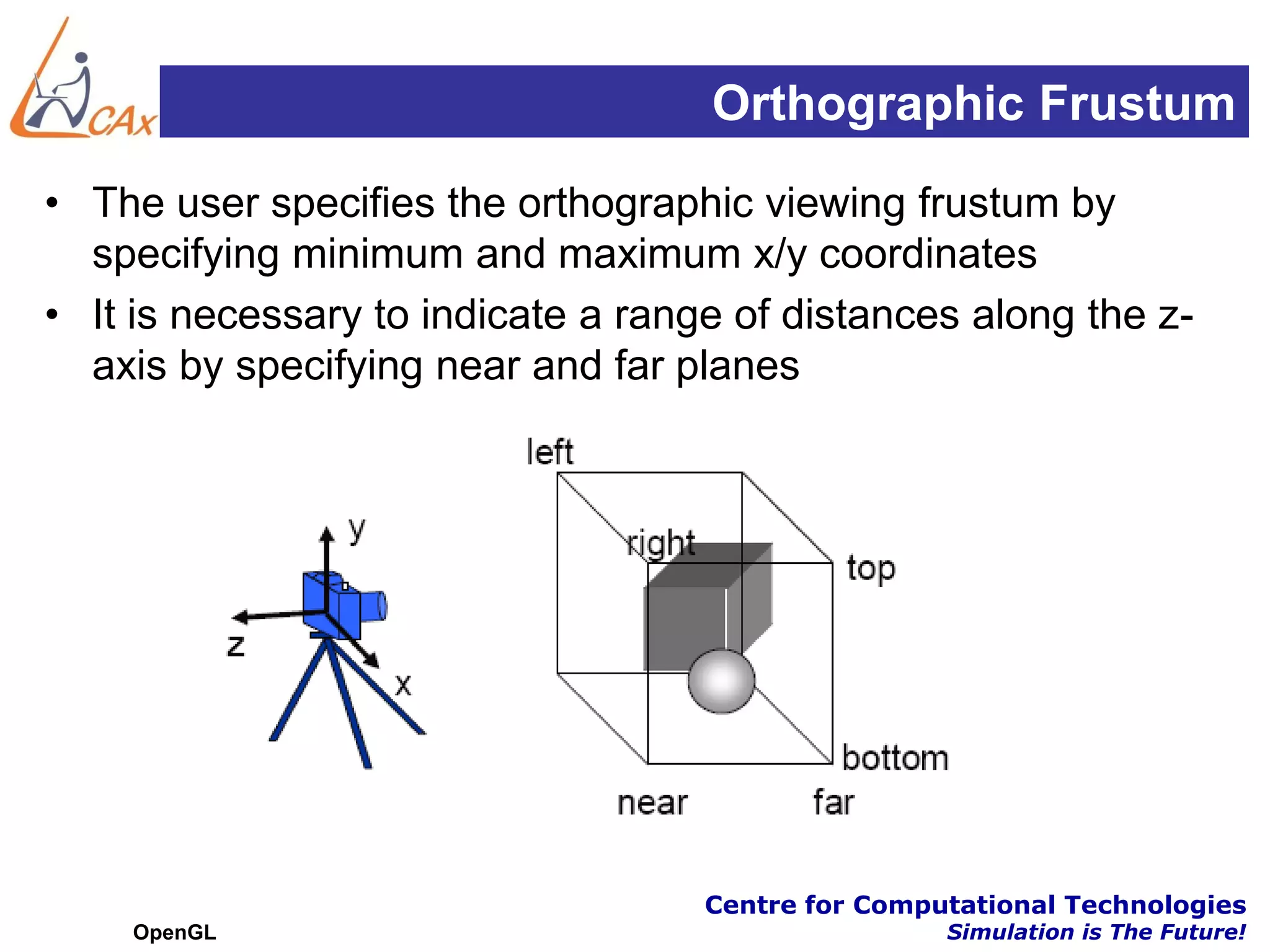
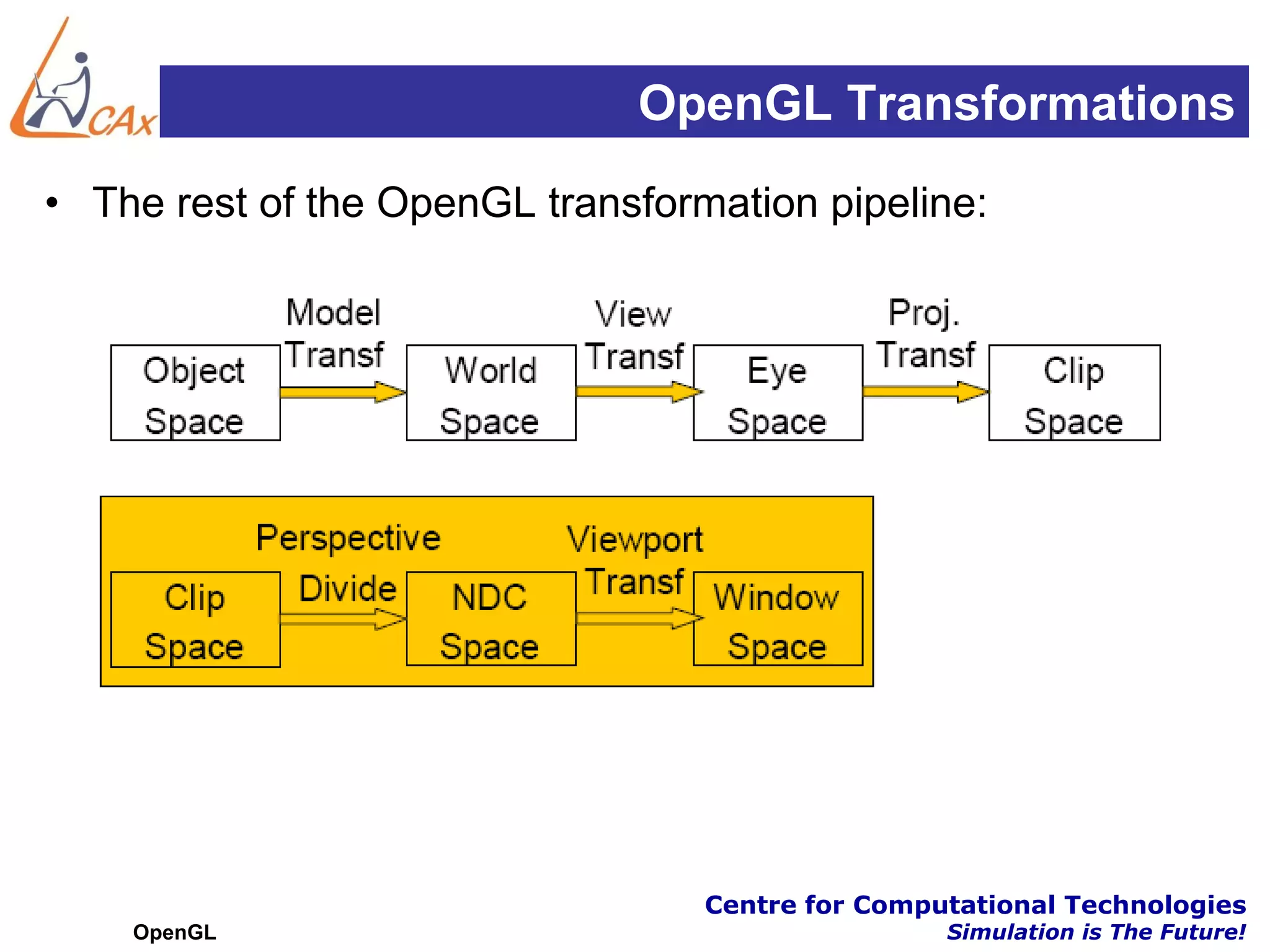
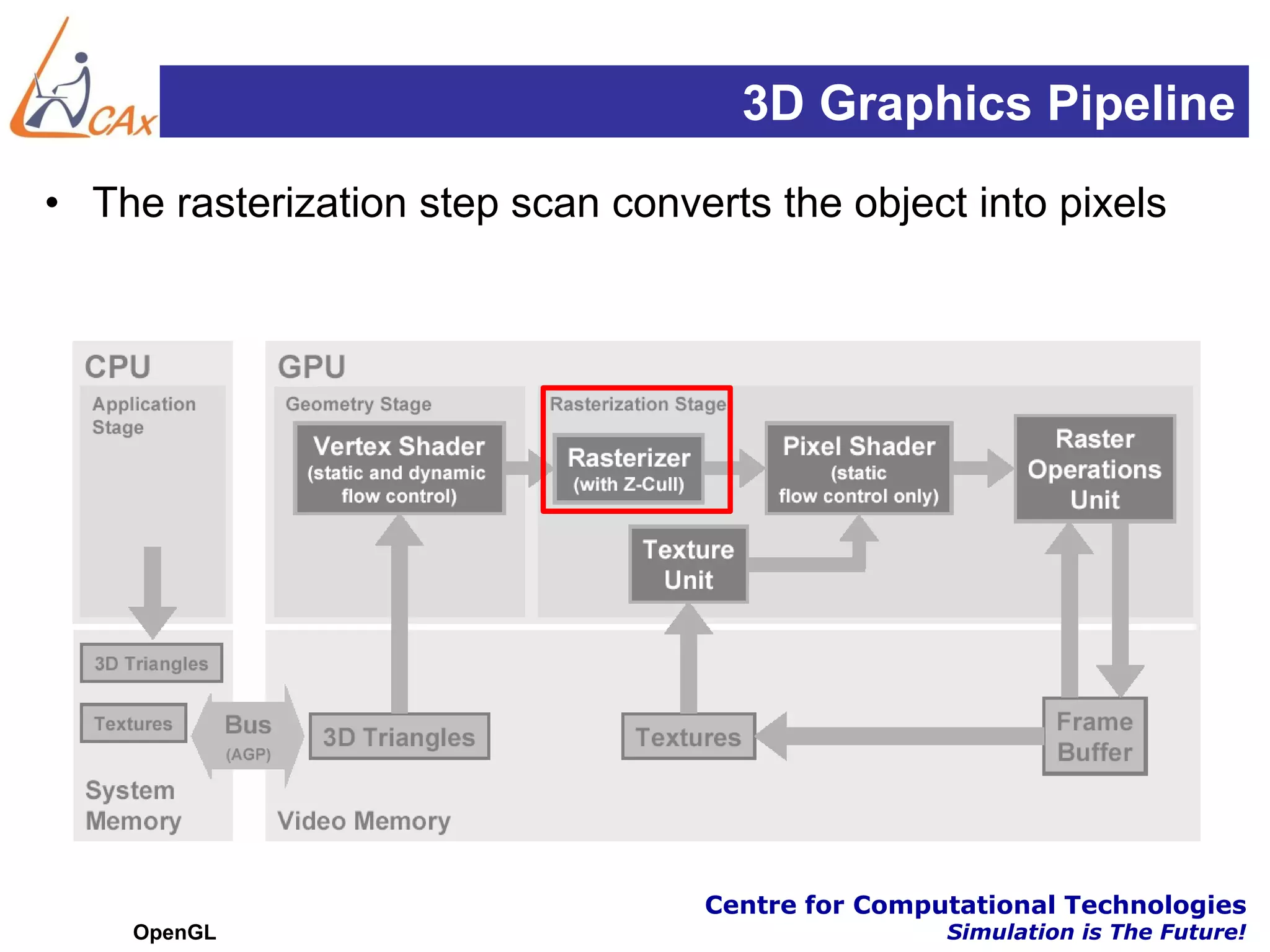
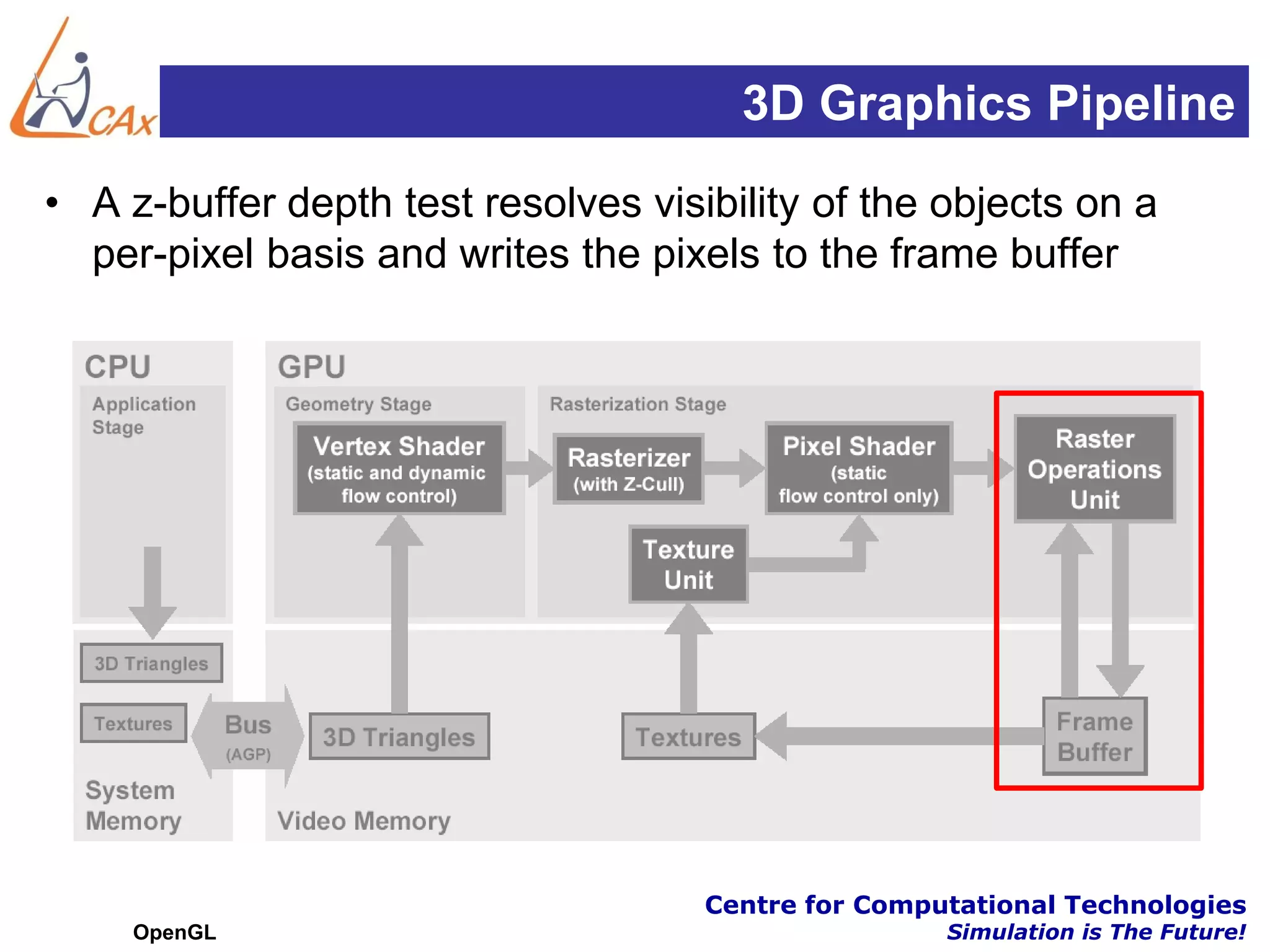
This document discusses OpenGL transformations. It describes how geometric objects are represented and transformed using matrices. Transformation matrices for modeling, viewing and projection are manipulated separately in OpenGL. The viewing transformation places the camera in the 3D world. Projection can be parallel (orthographic) or perspective, with perspective being more realistic. OpenGL provides functions for common viewing and projection setups. The full transformation pipeline involves clipping, perspective division, viewport mapping and rasterization to render the 3D scene to a 2D framebuffer.