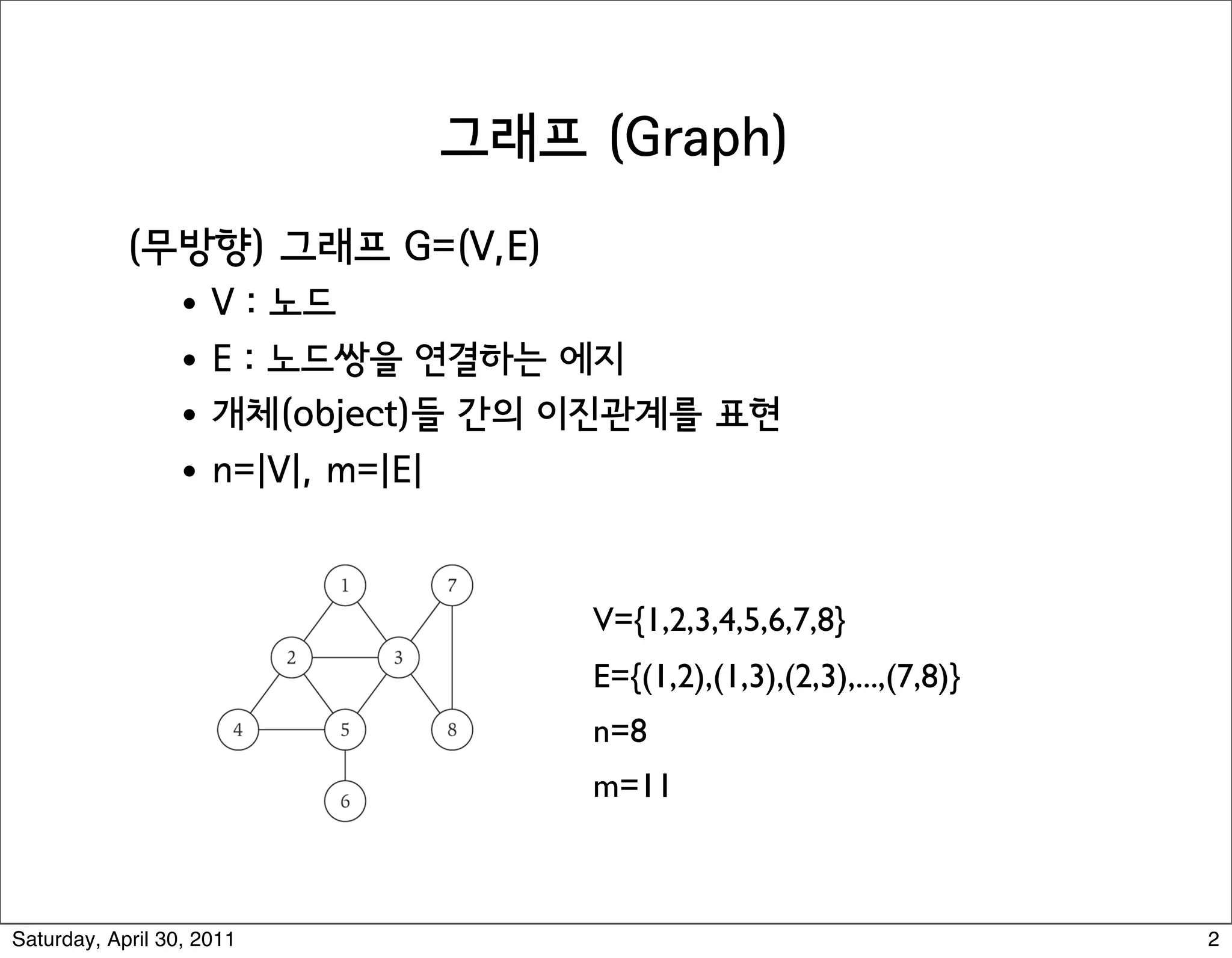
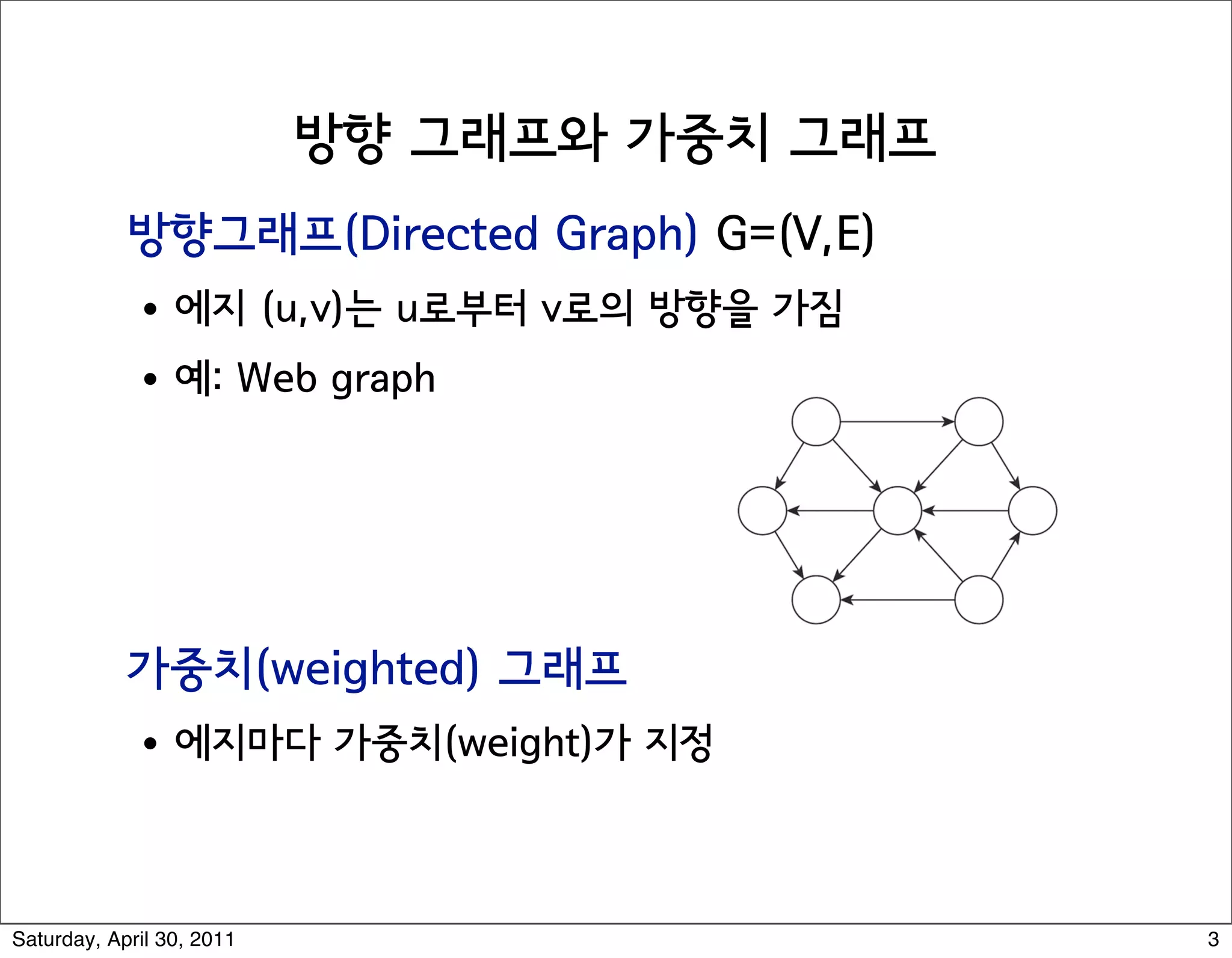
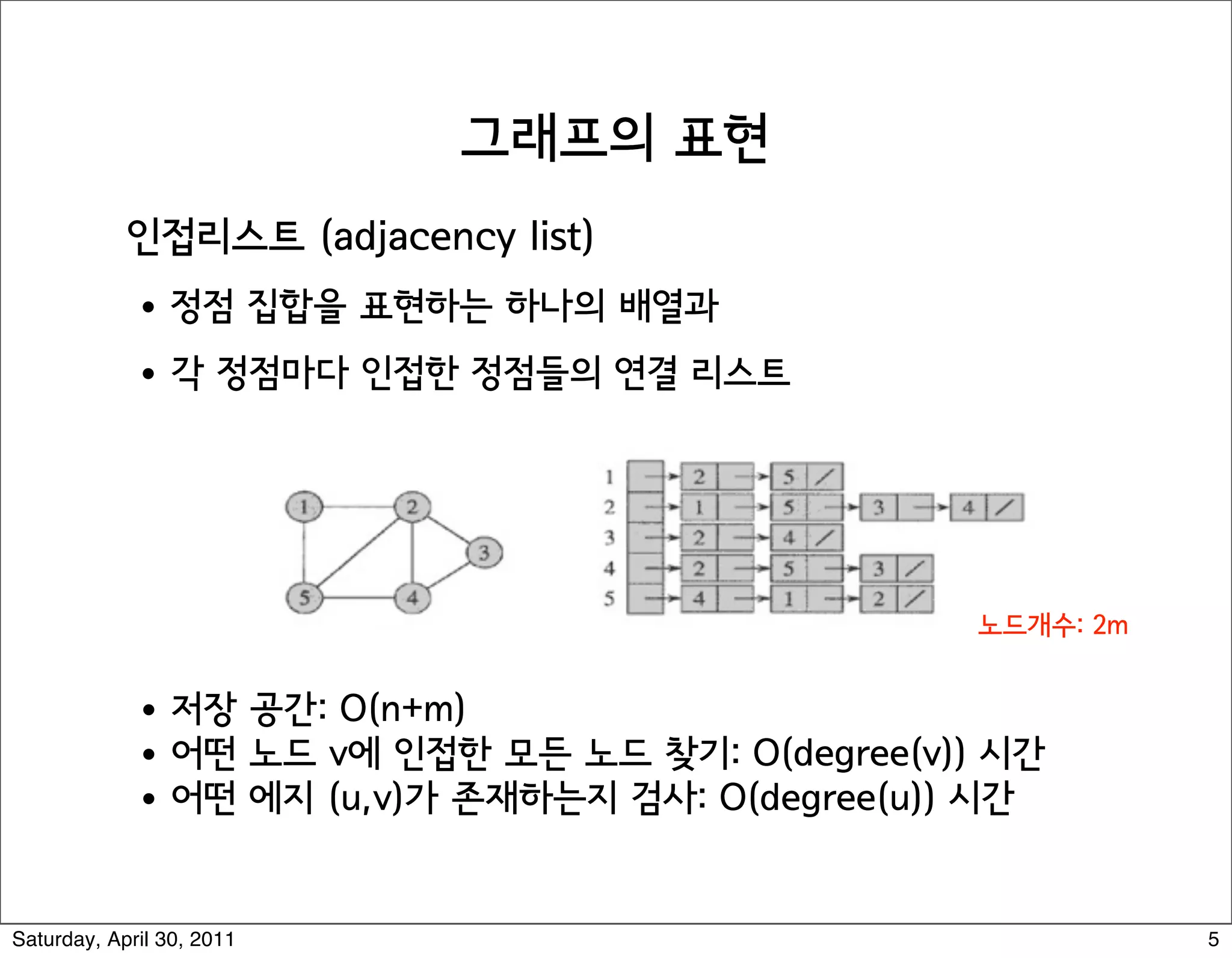
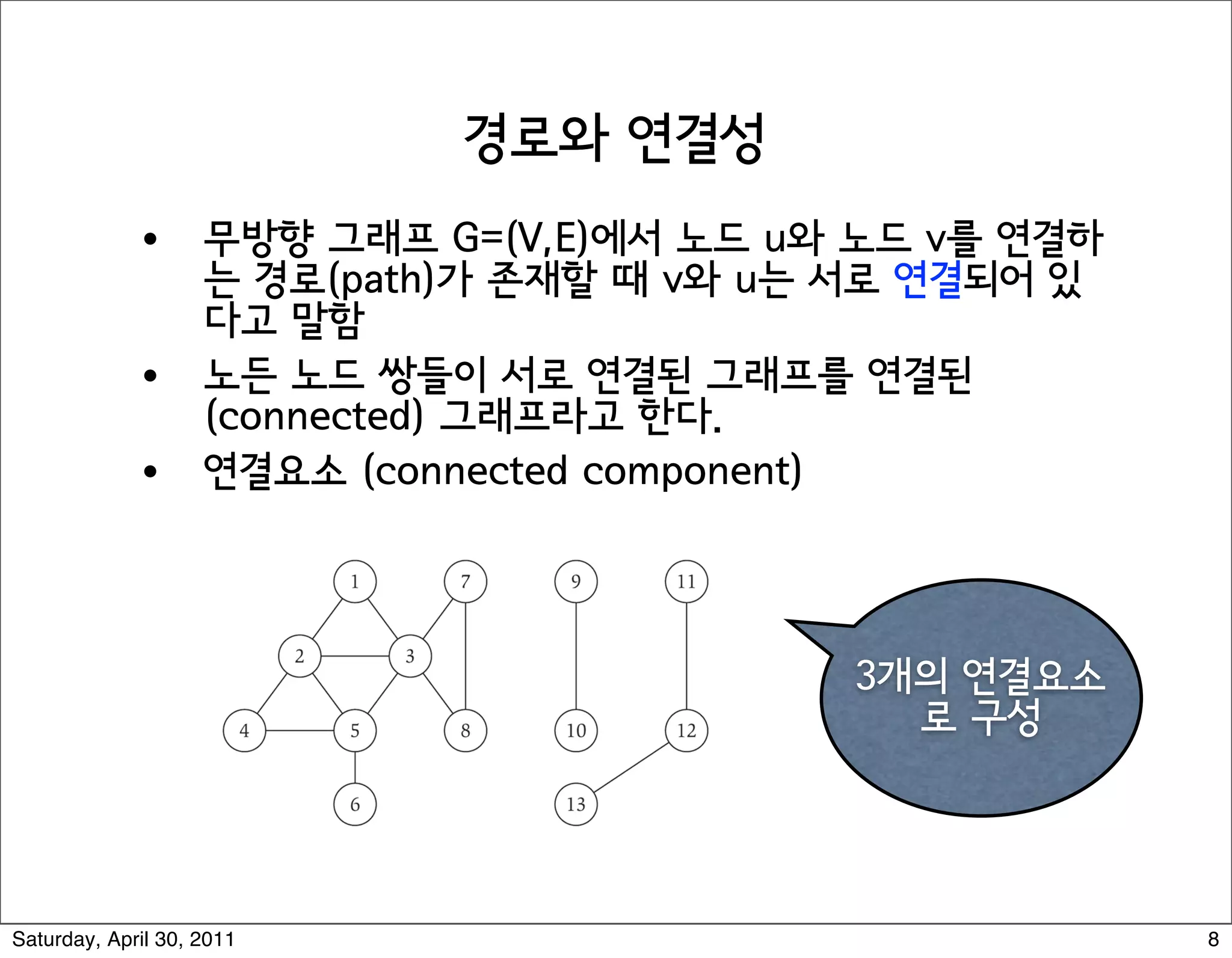
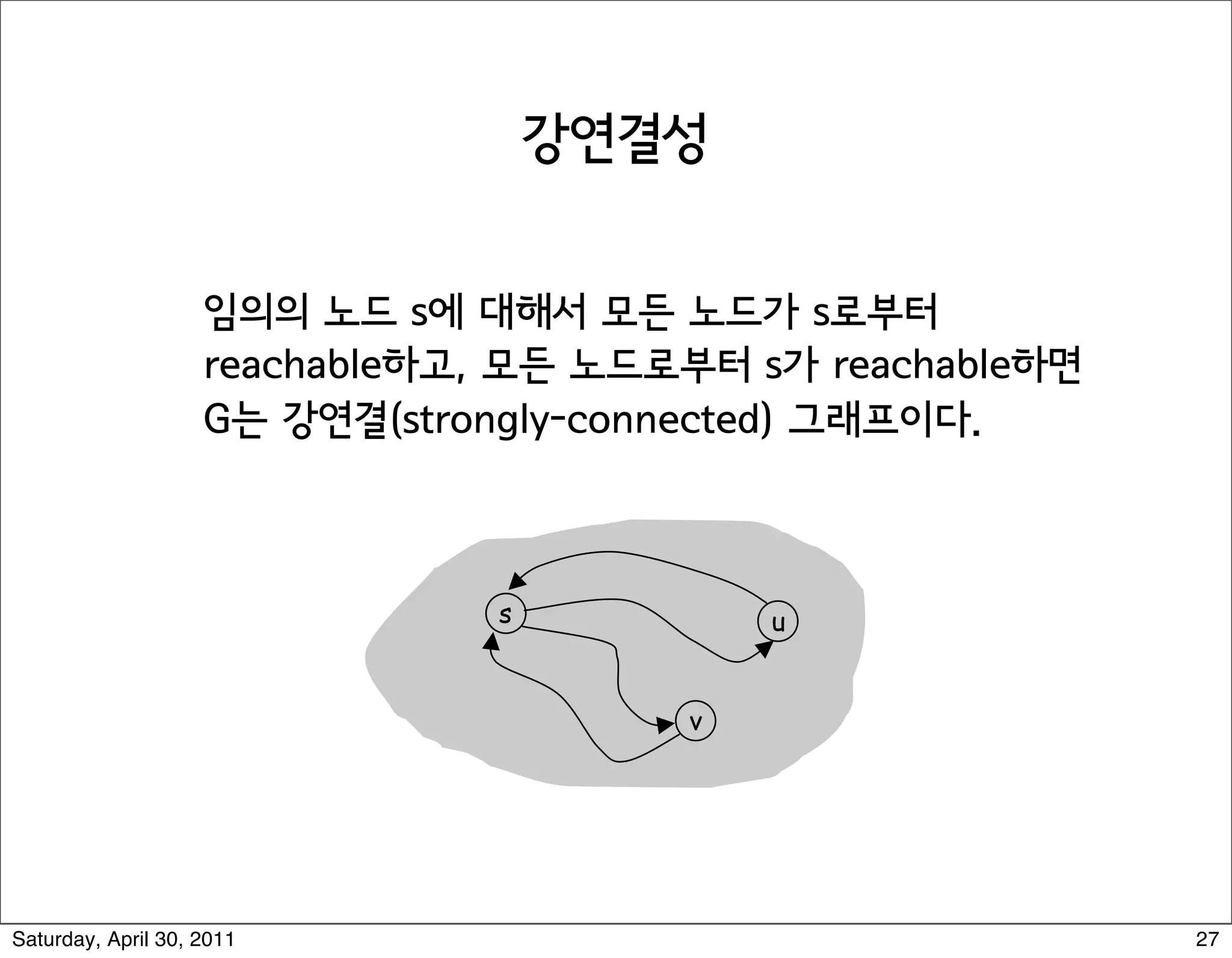
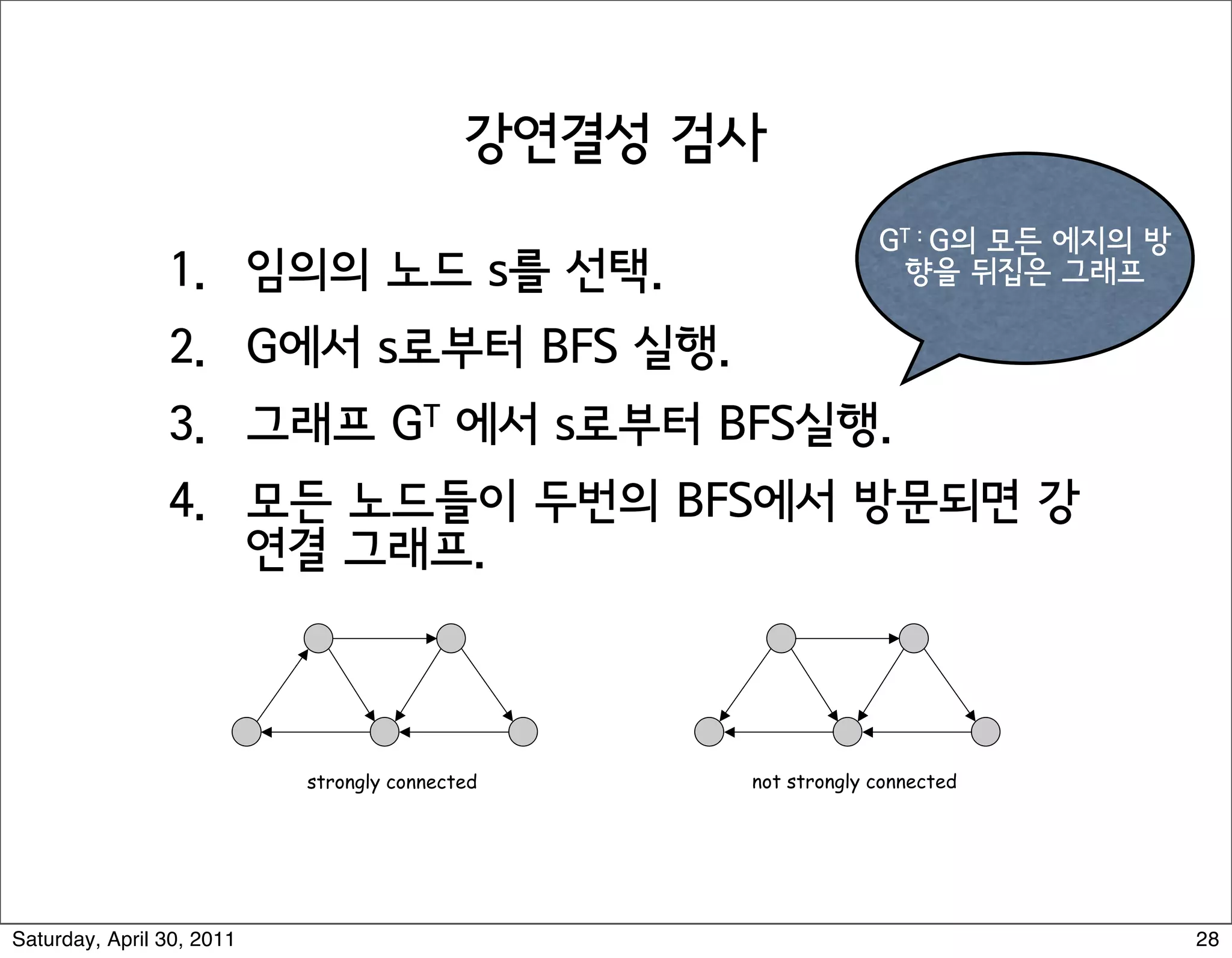
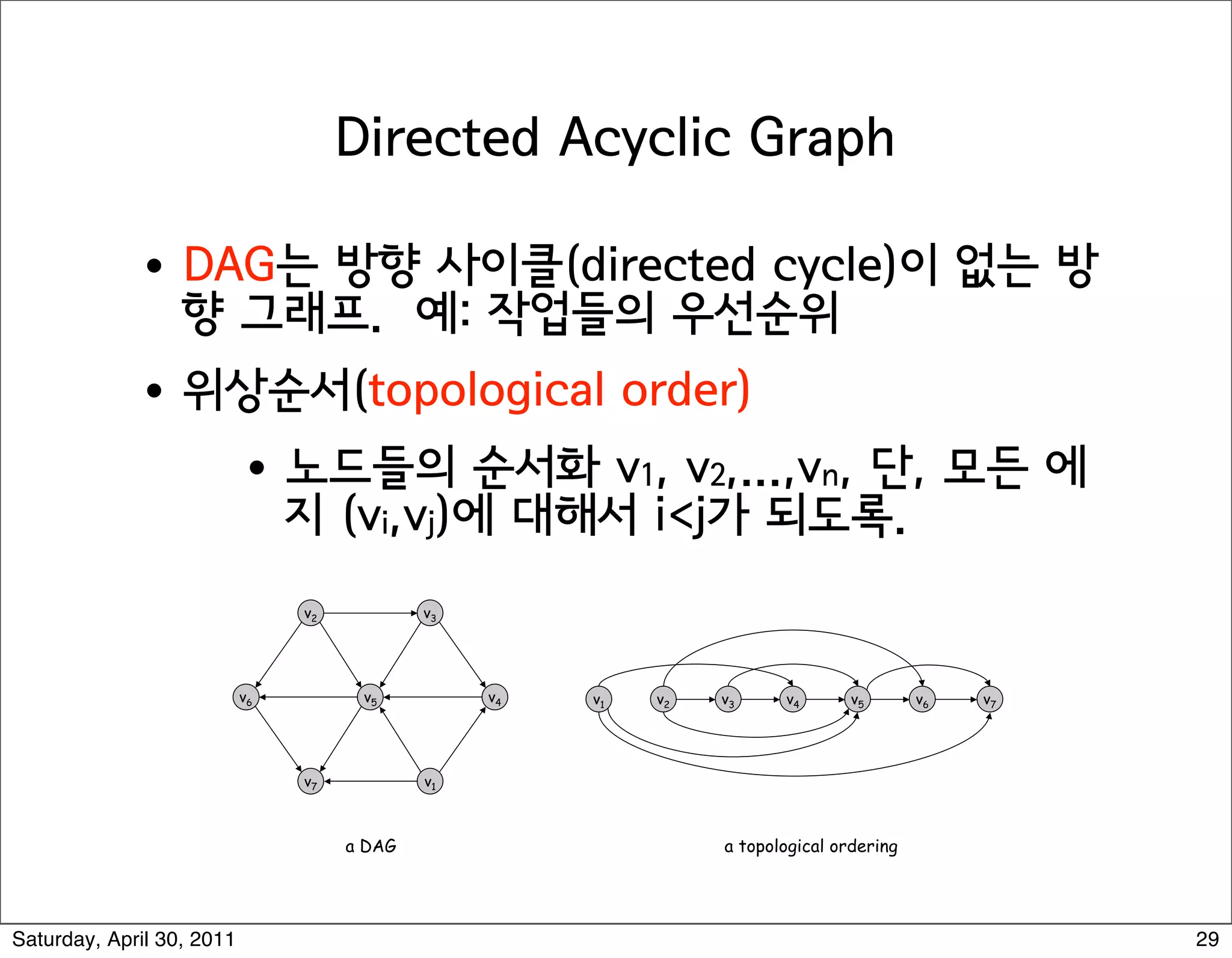
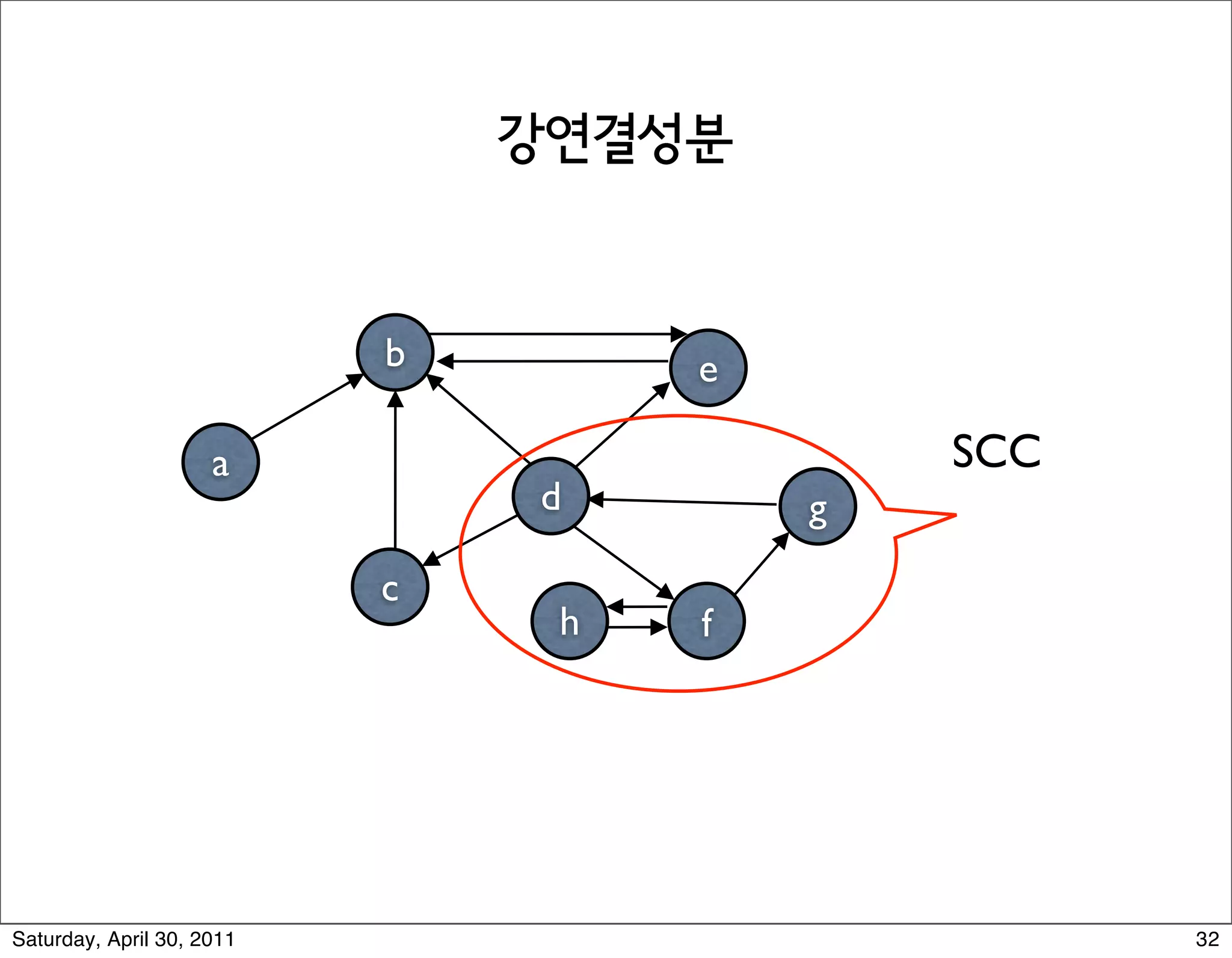
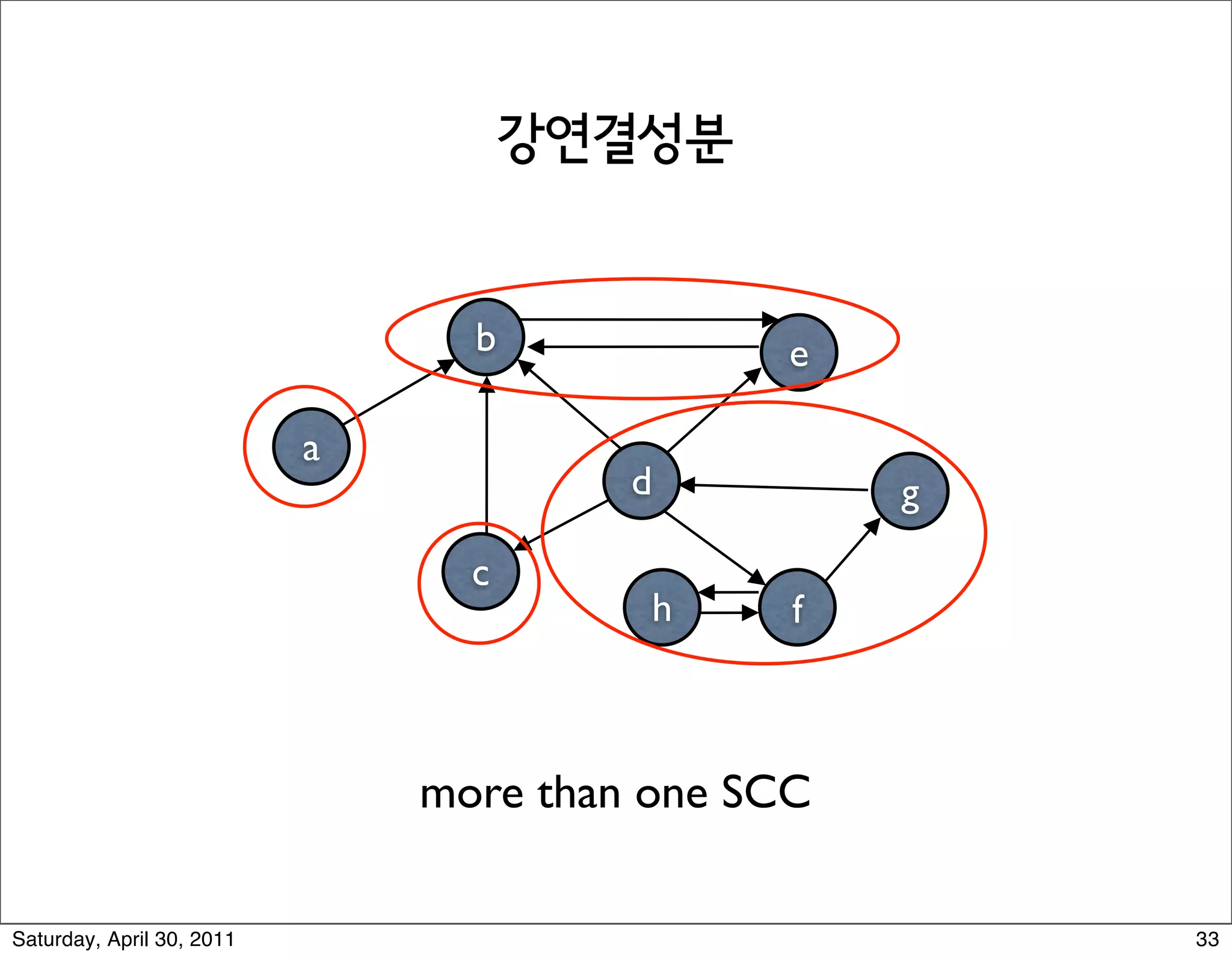
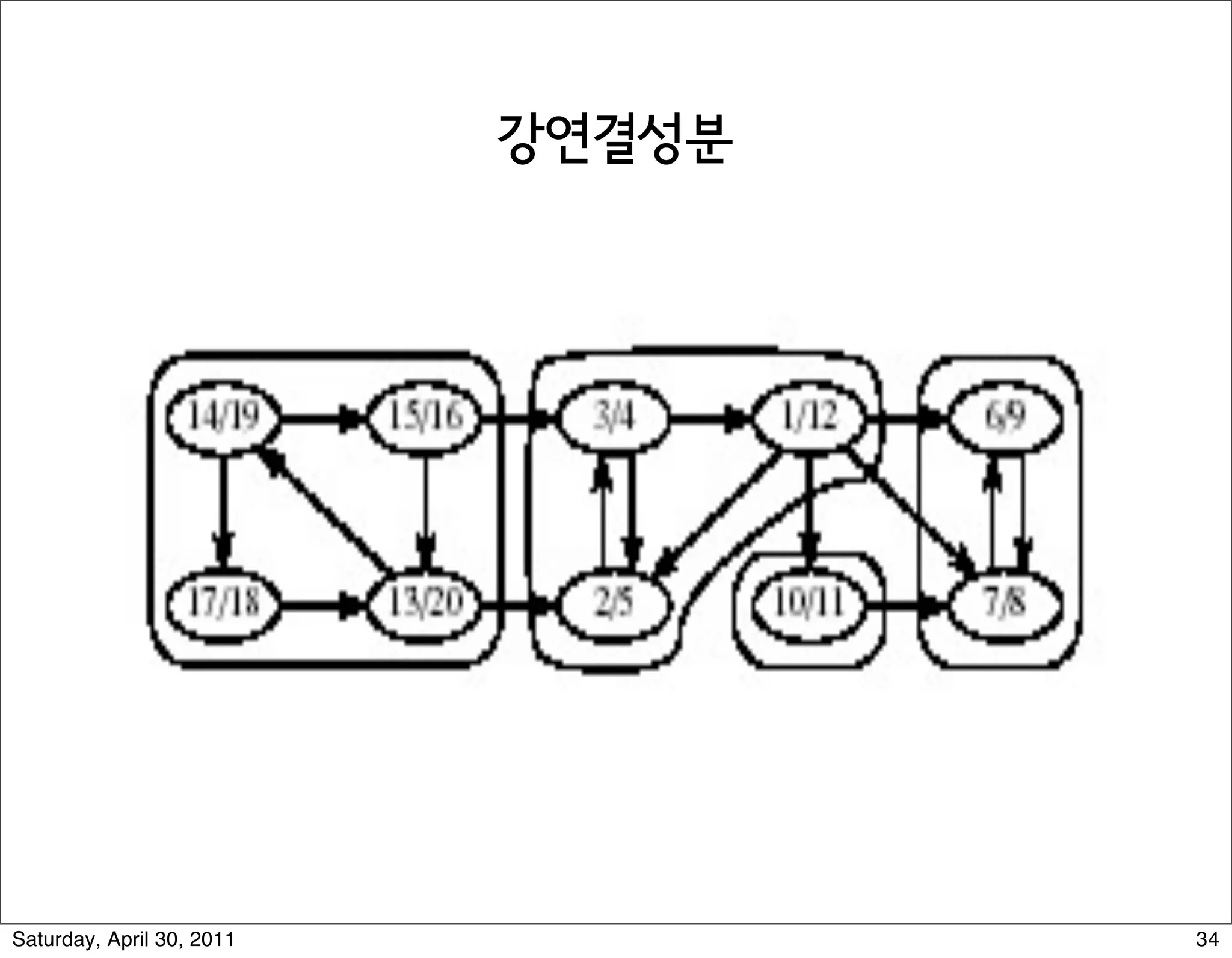
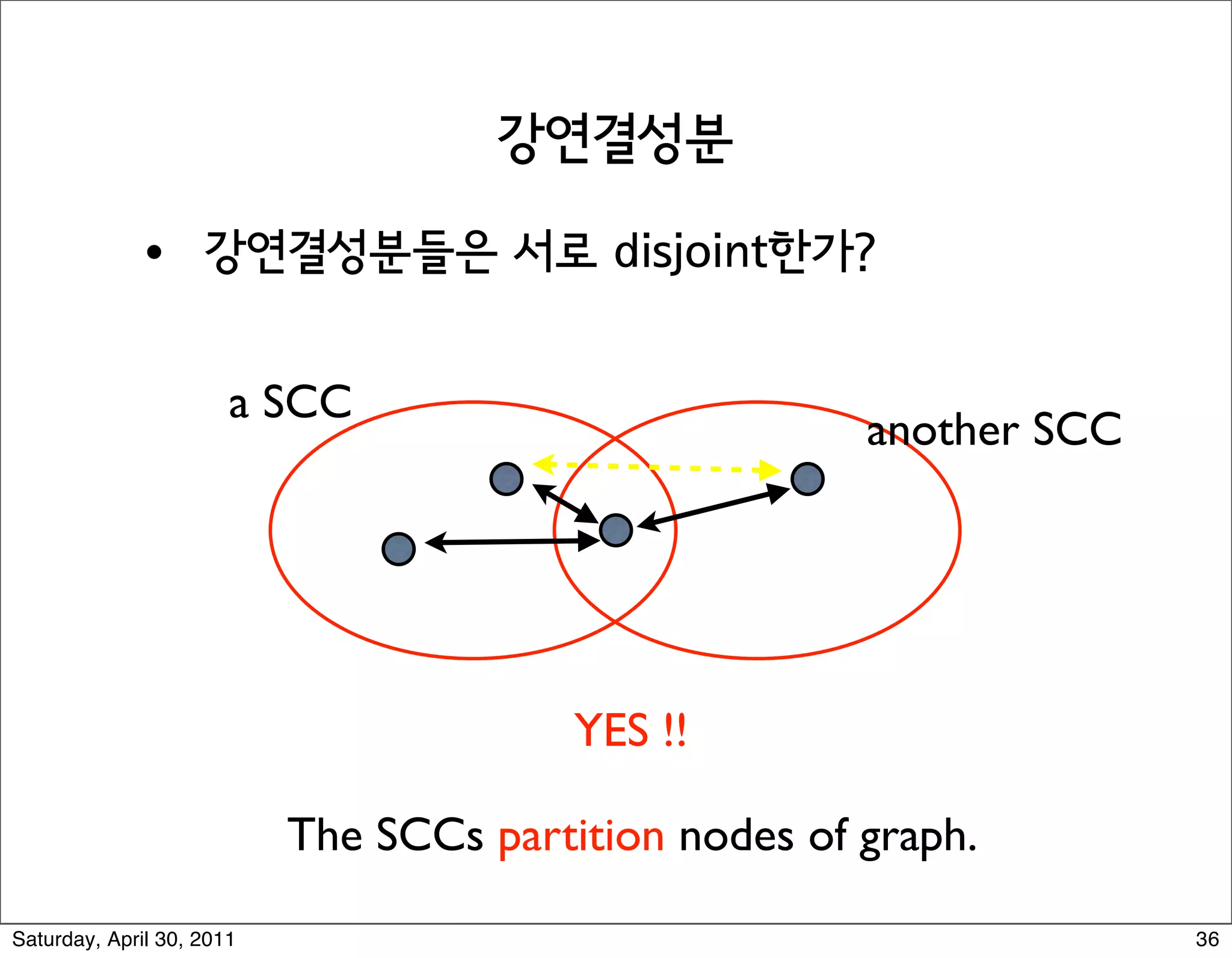
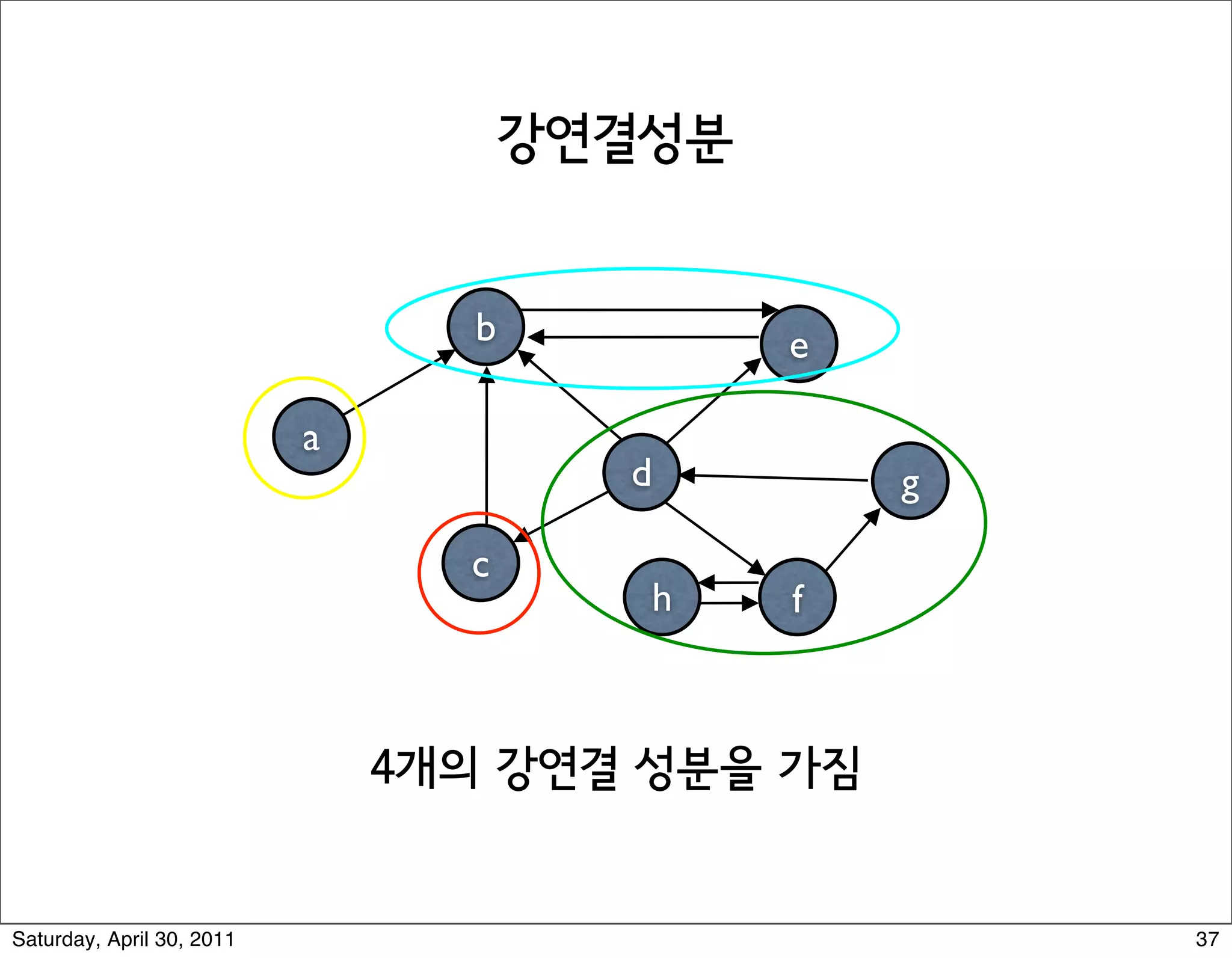
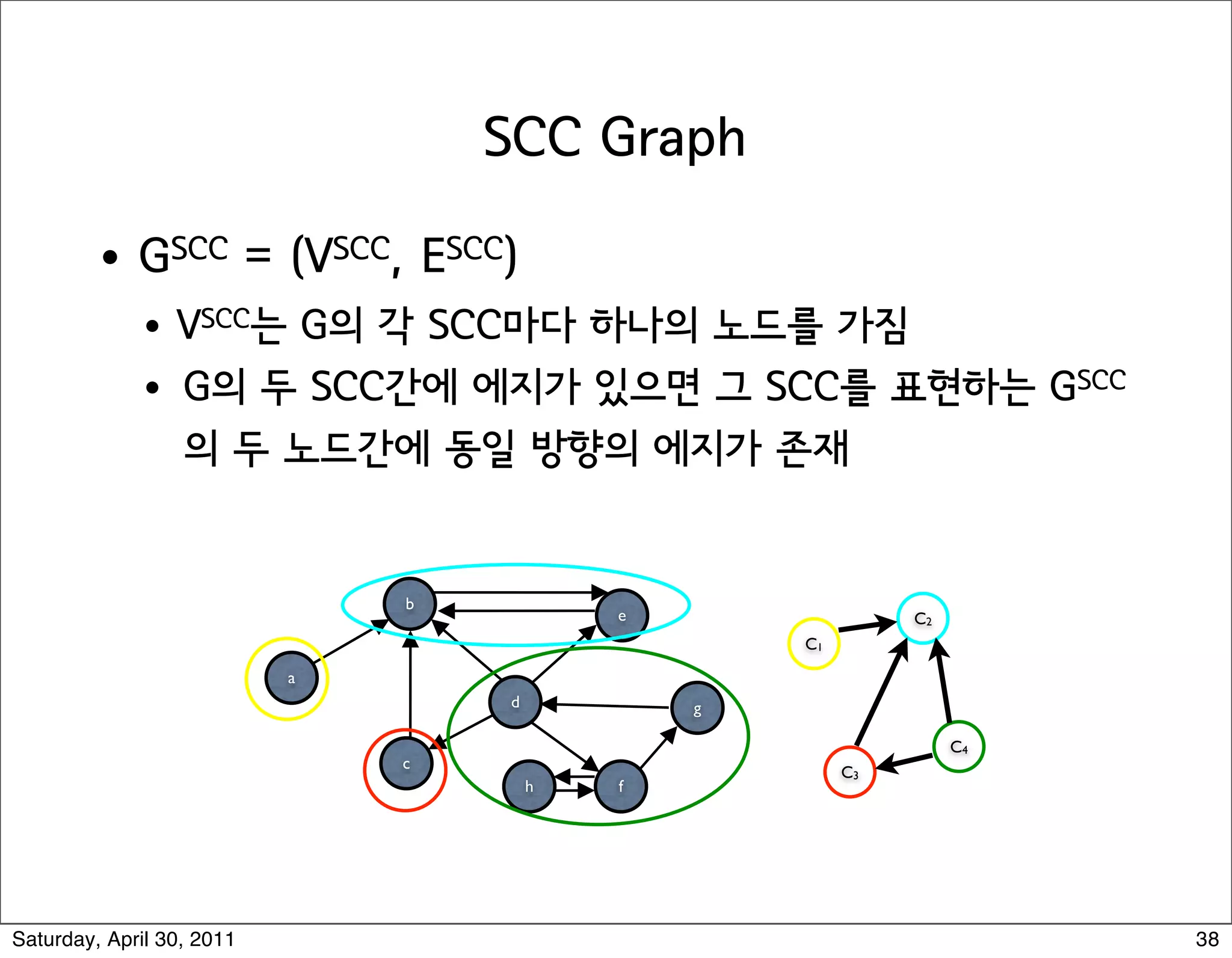
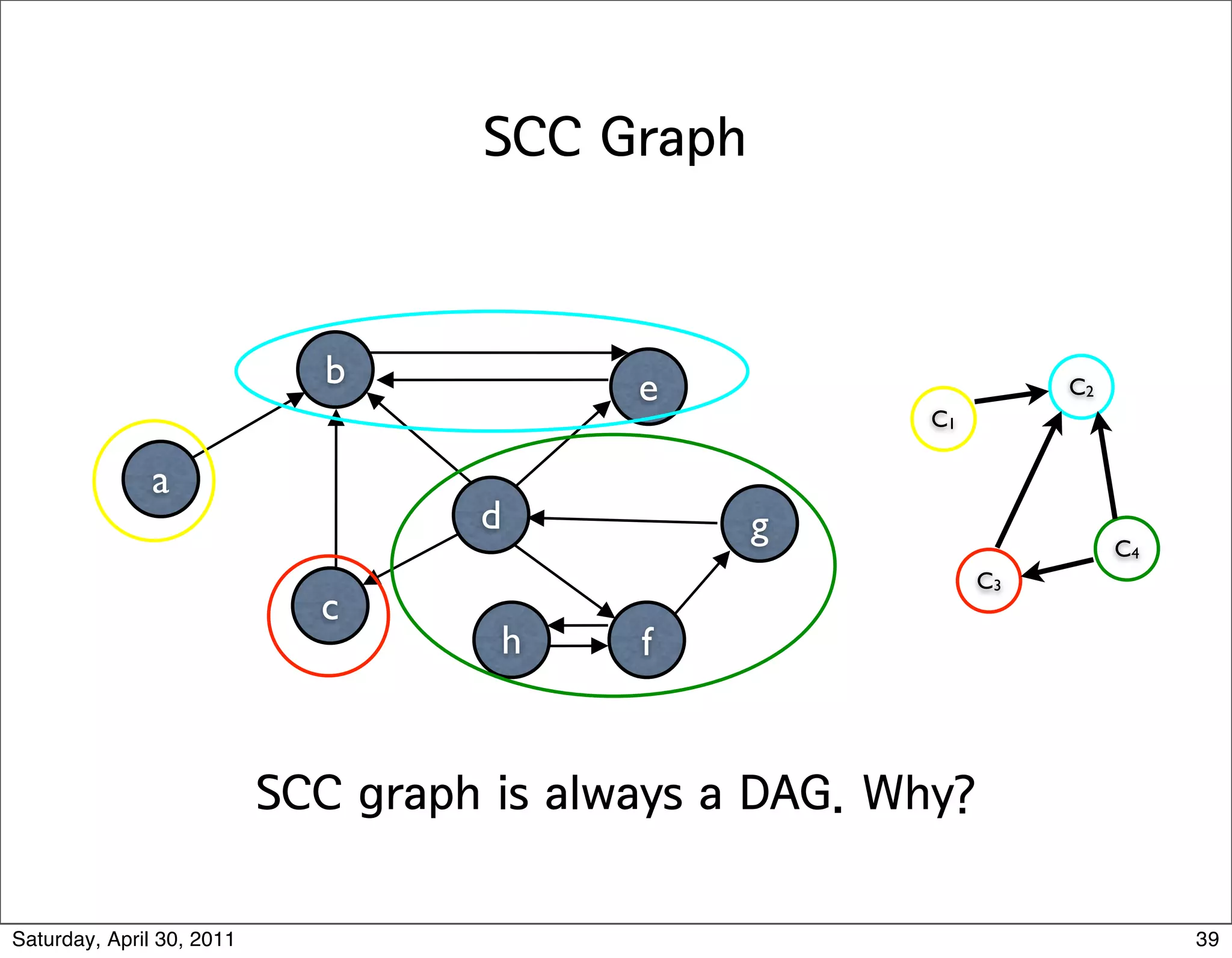
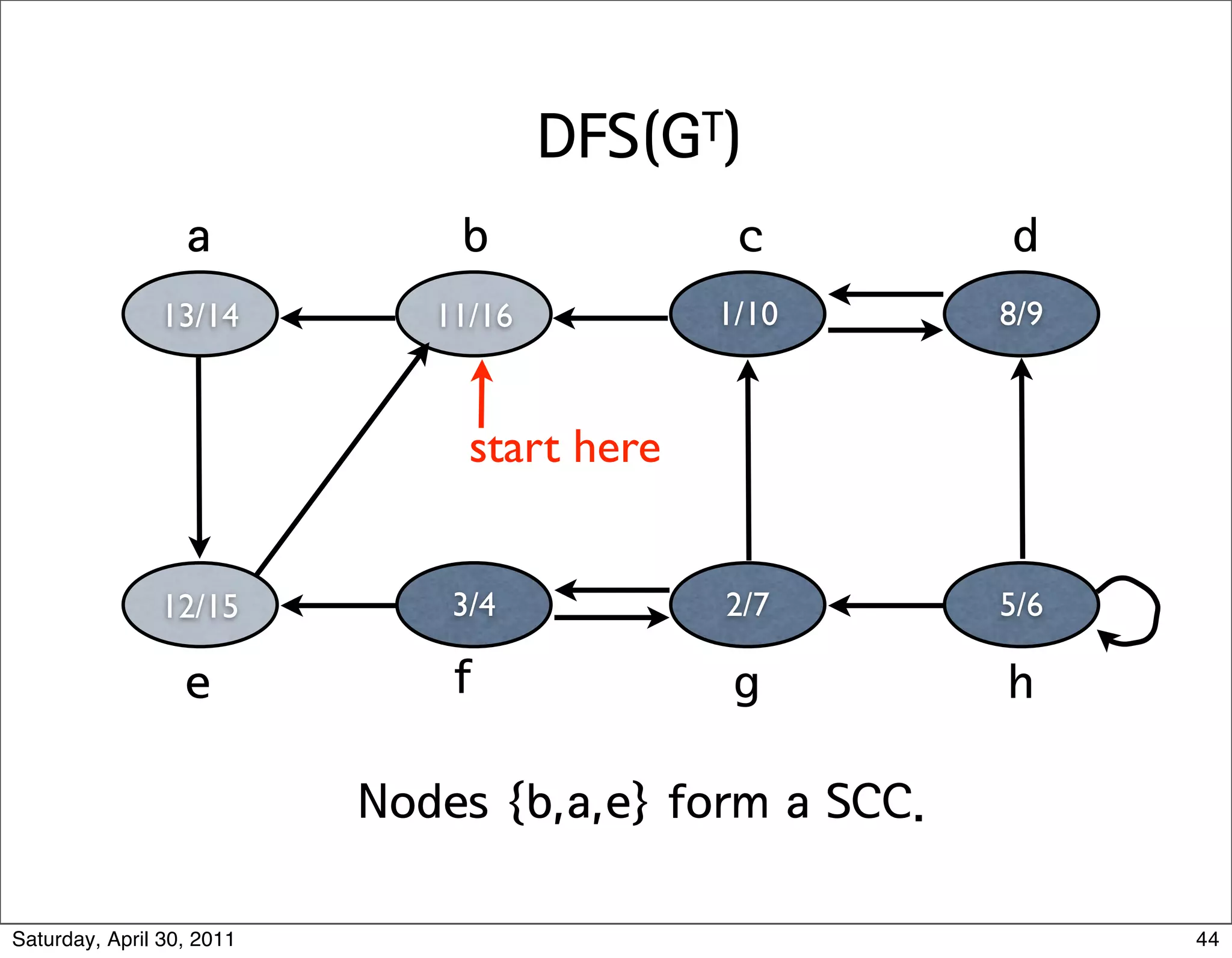
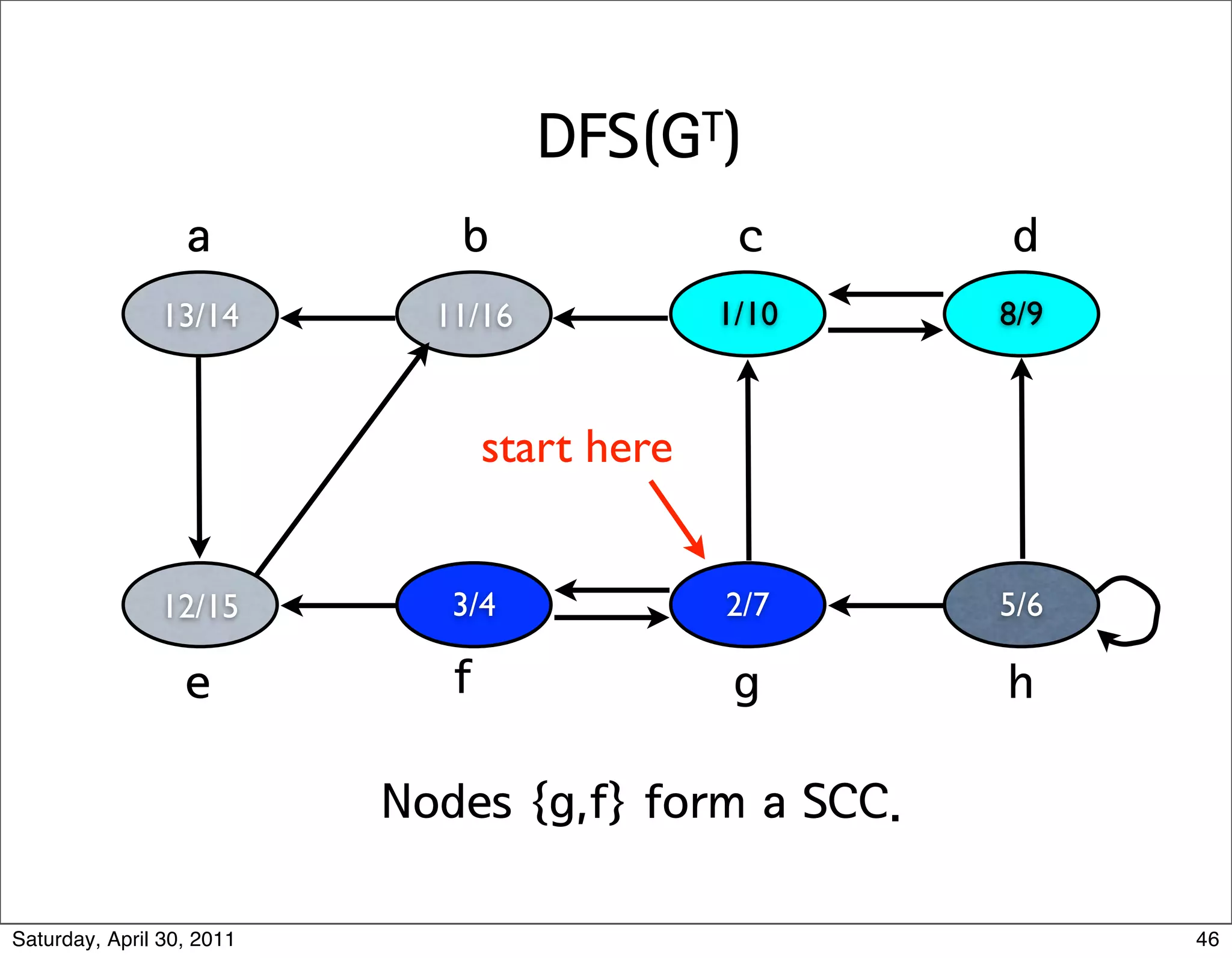
The document discusses various graph algorithms and representations including:
1) Undirected and directed graphs represented by adjacency matrices which take O(n^2) space and O(1) time to check edges.
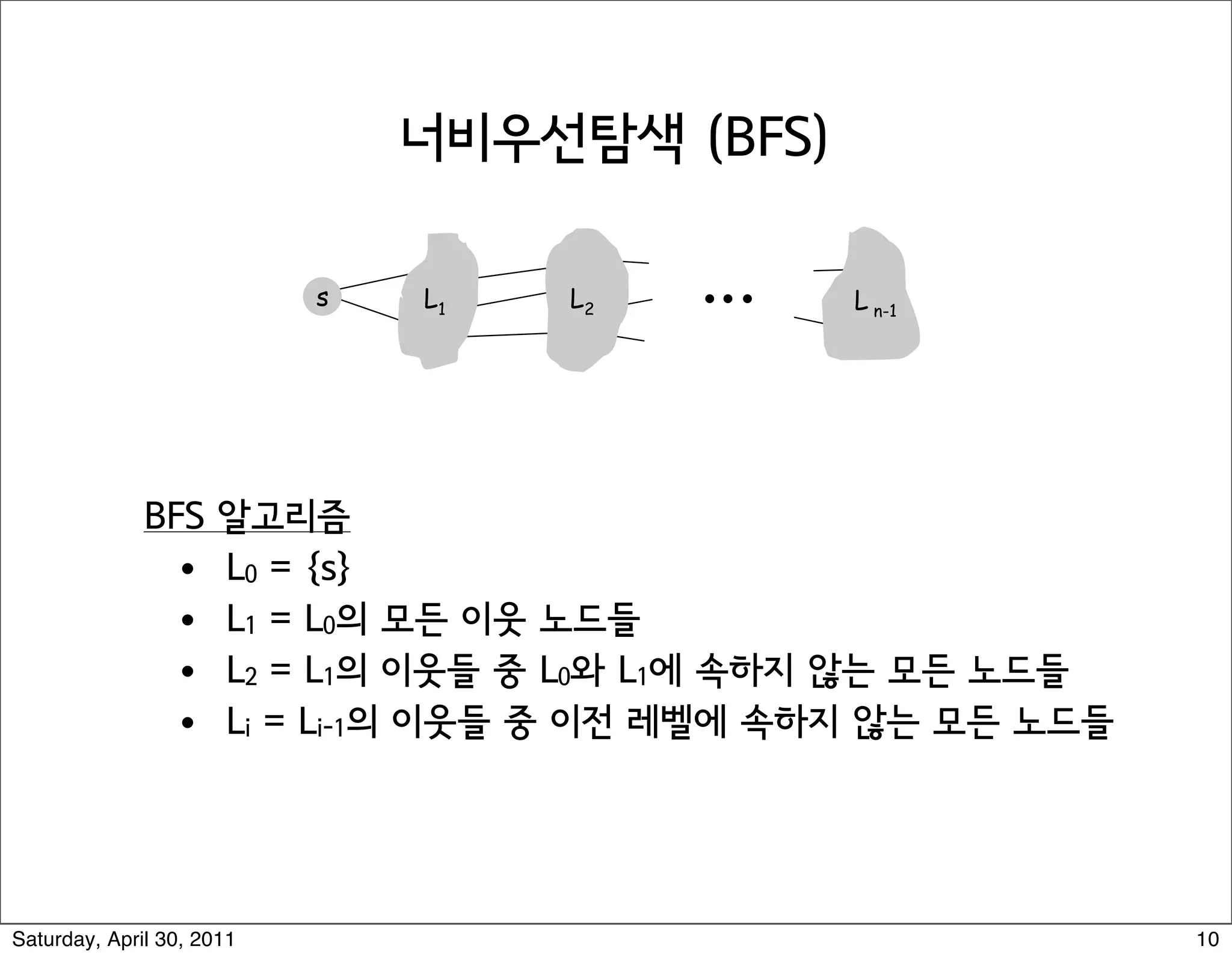
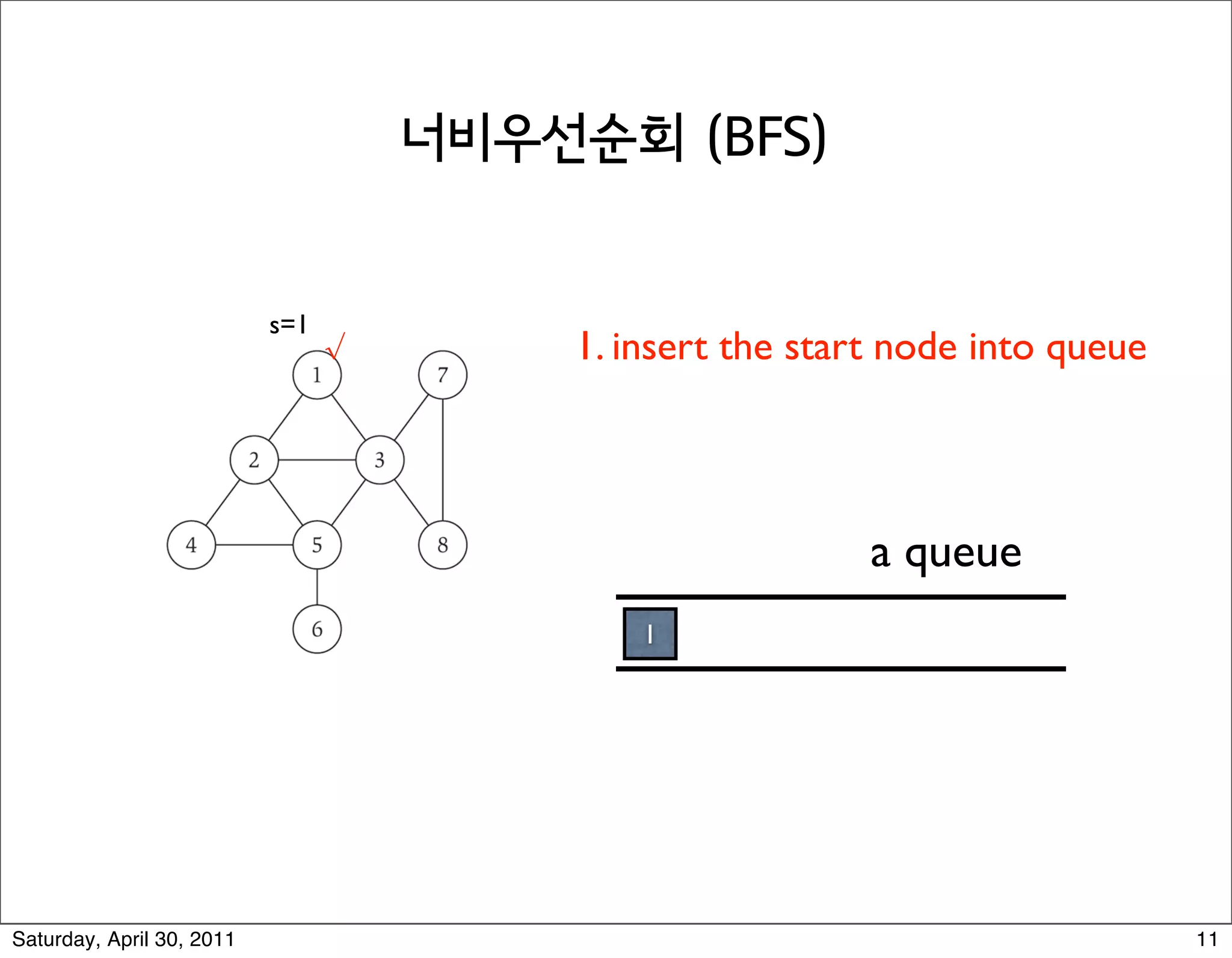
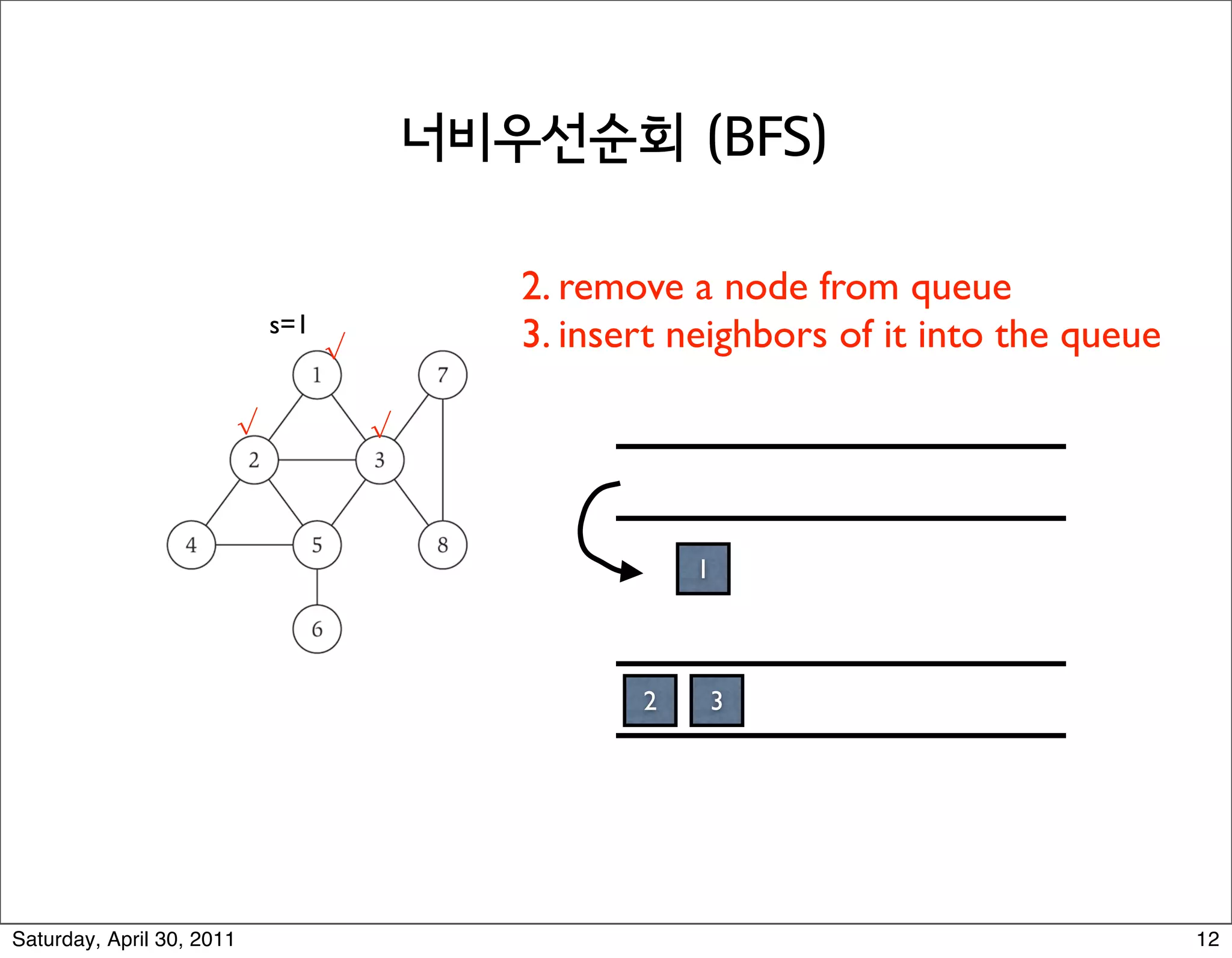
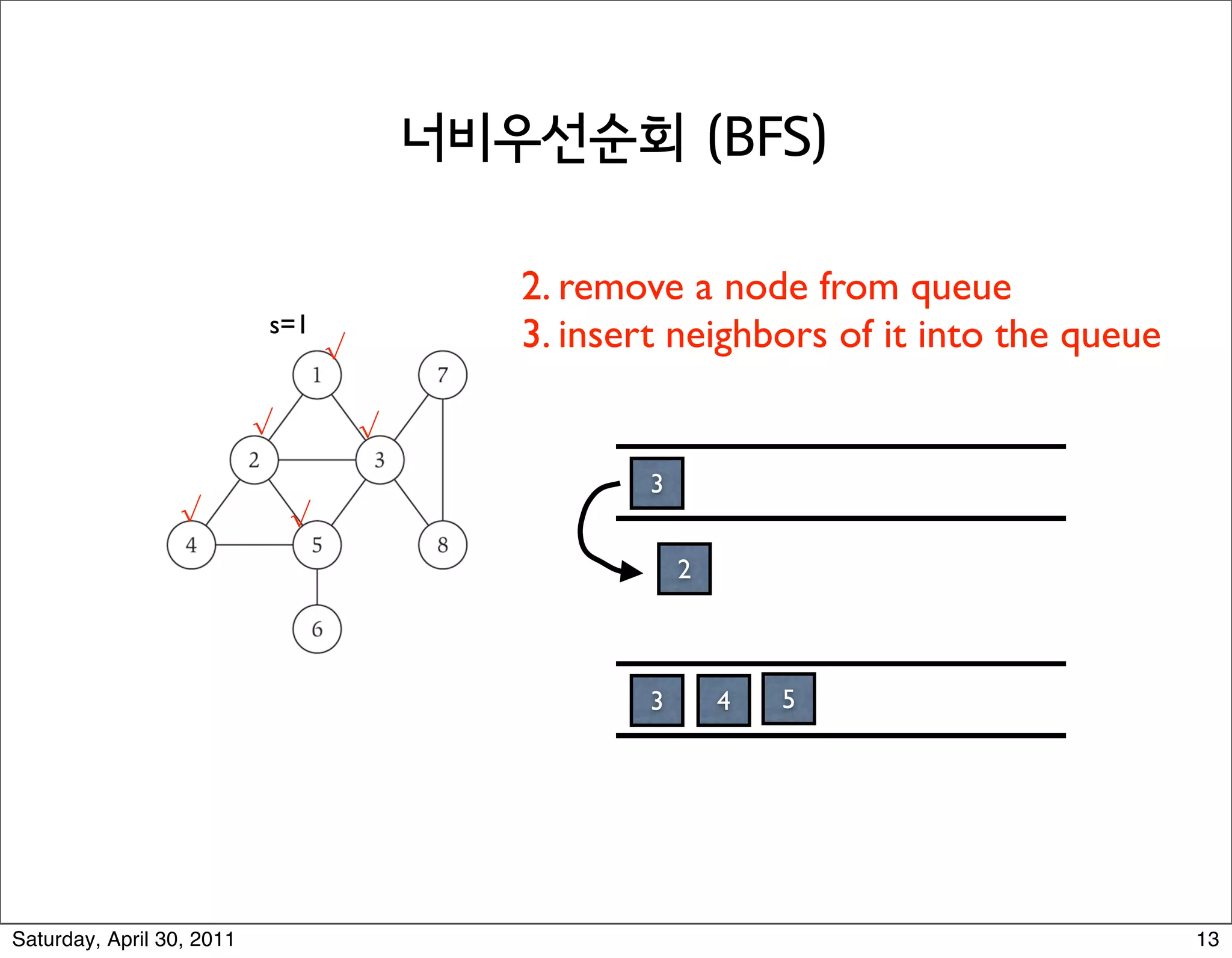
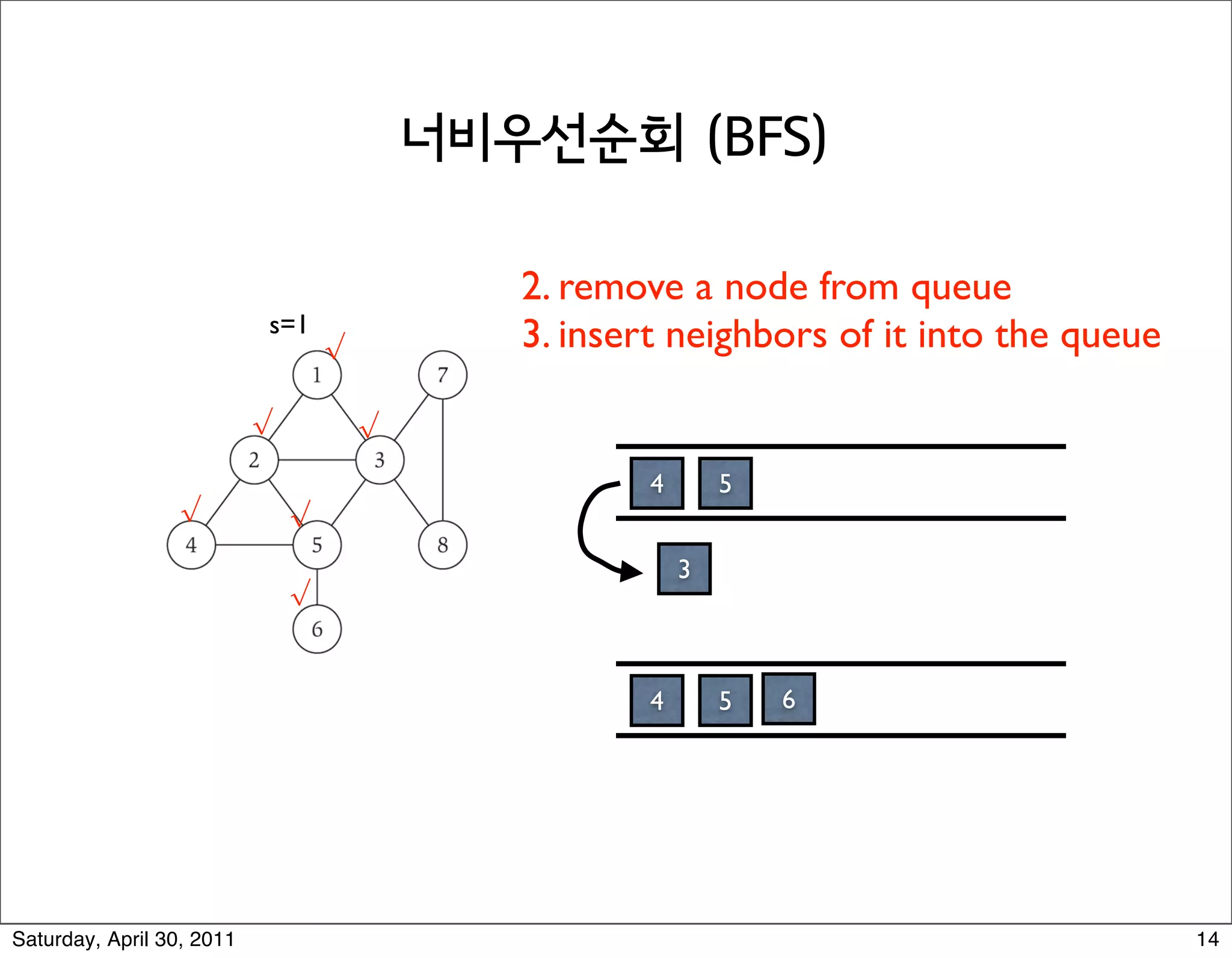
2) Breadth-first search (BFS) which explores the graph outwards from the source node in layers, finding all nodes at distance i before i+1.
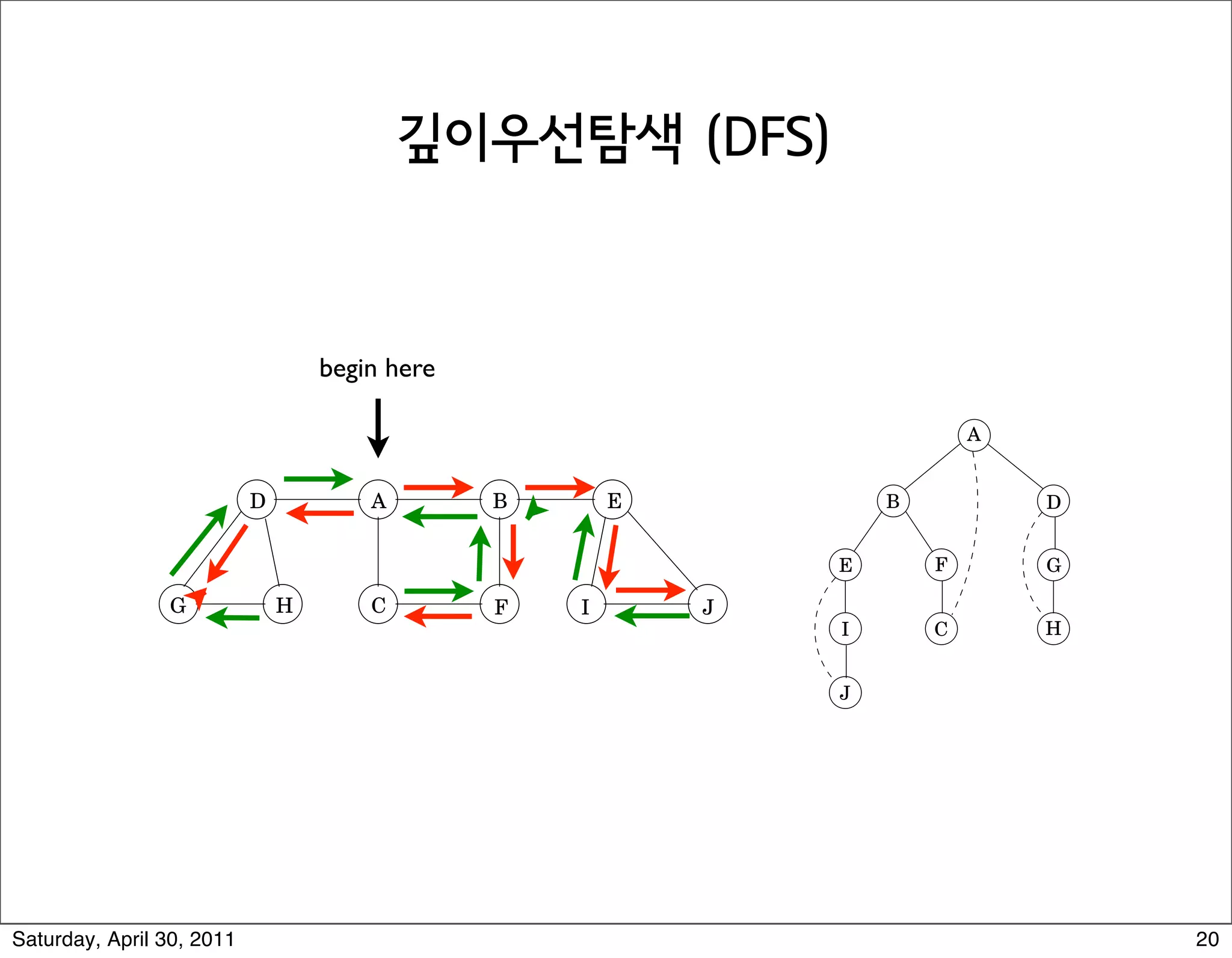
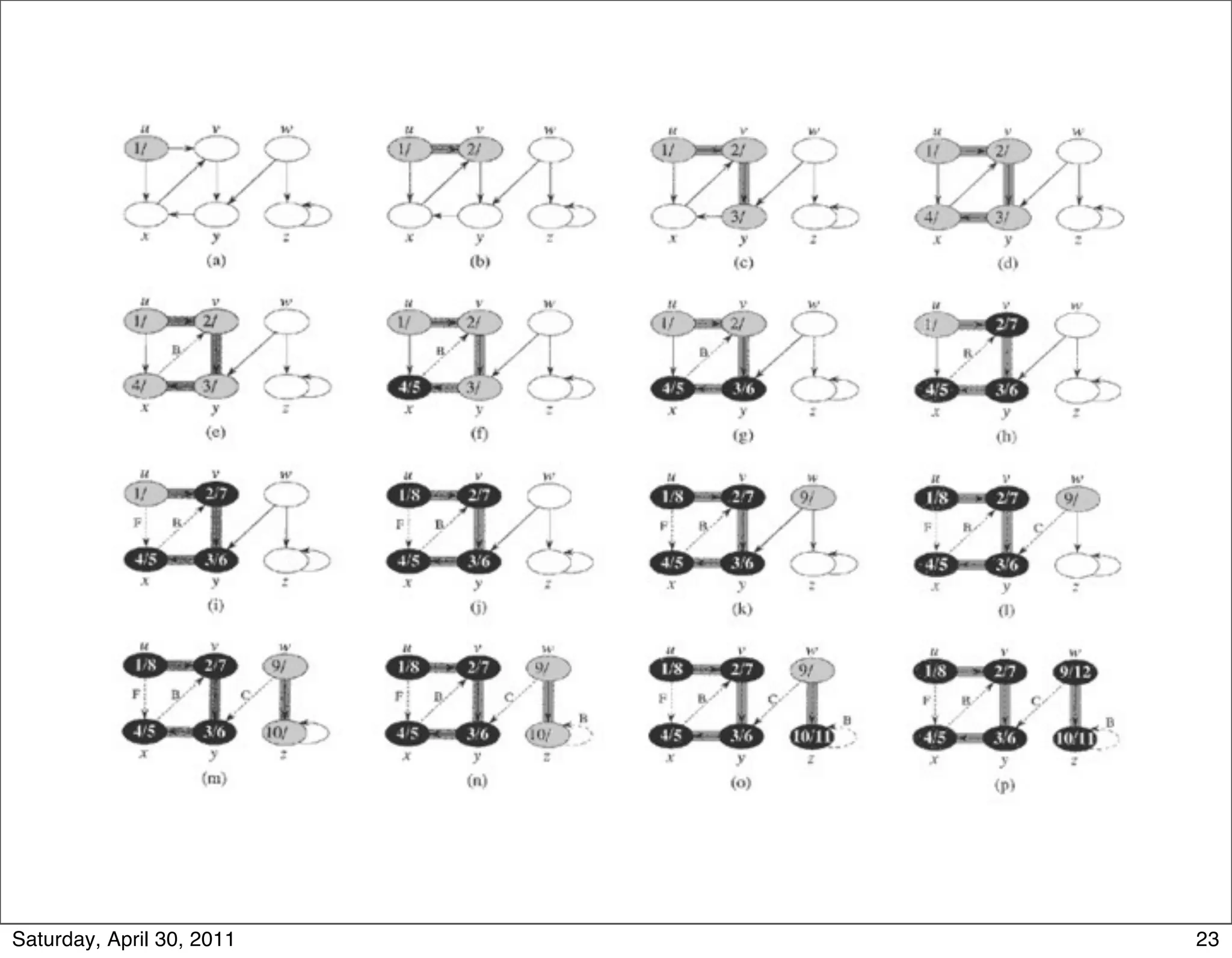
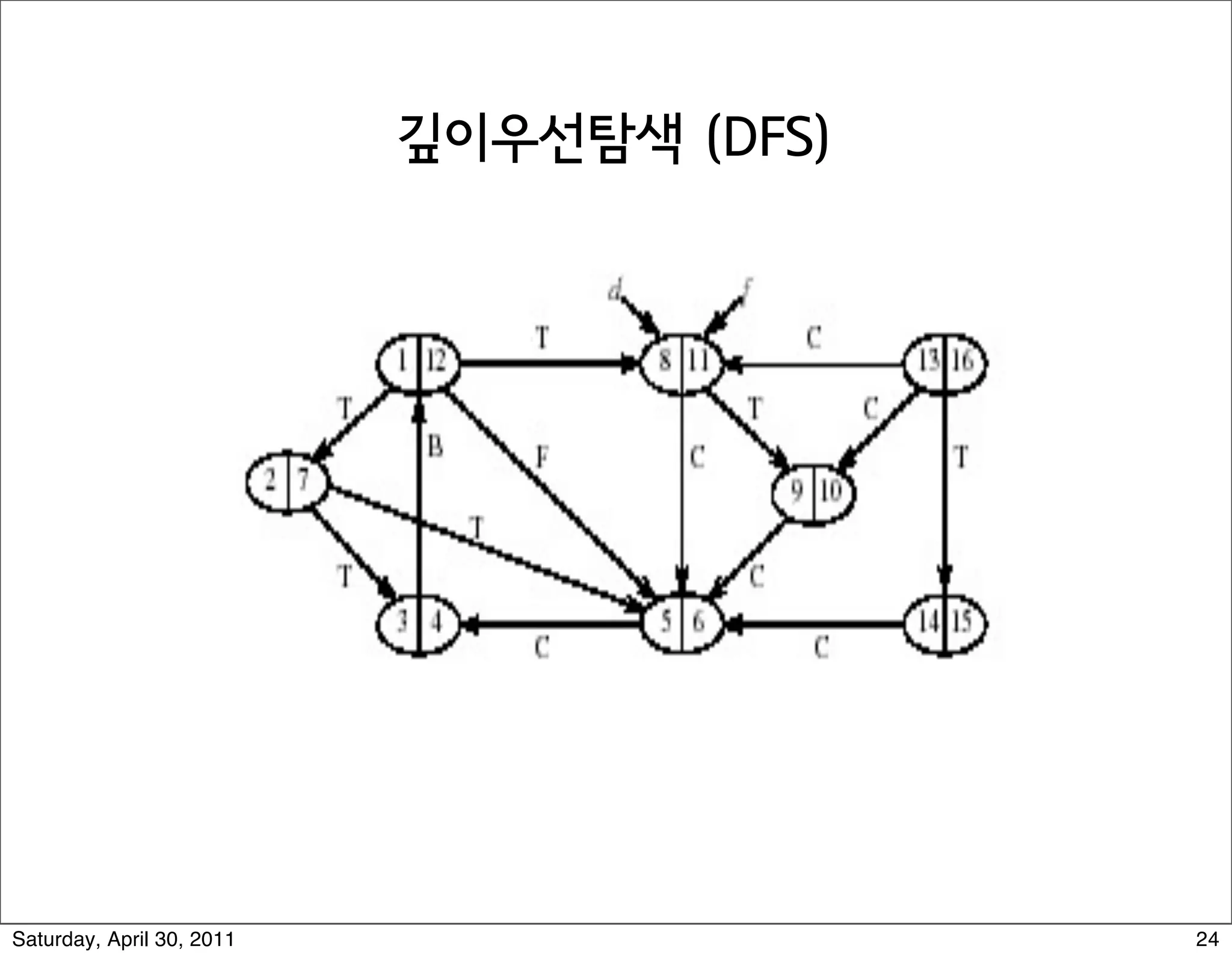
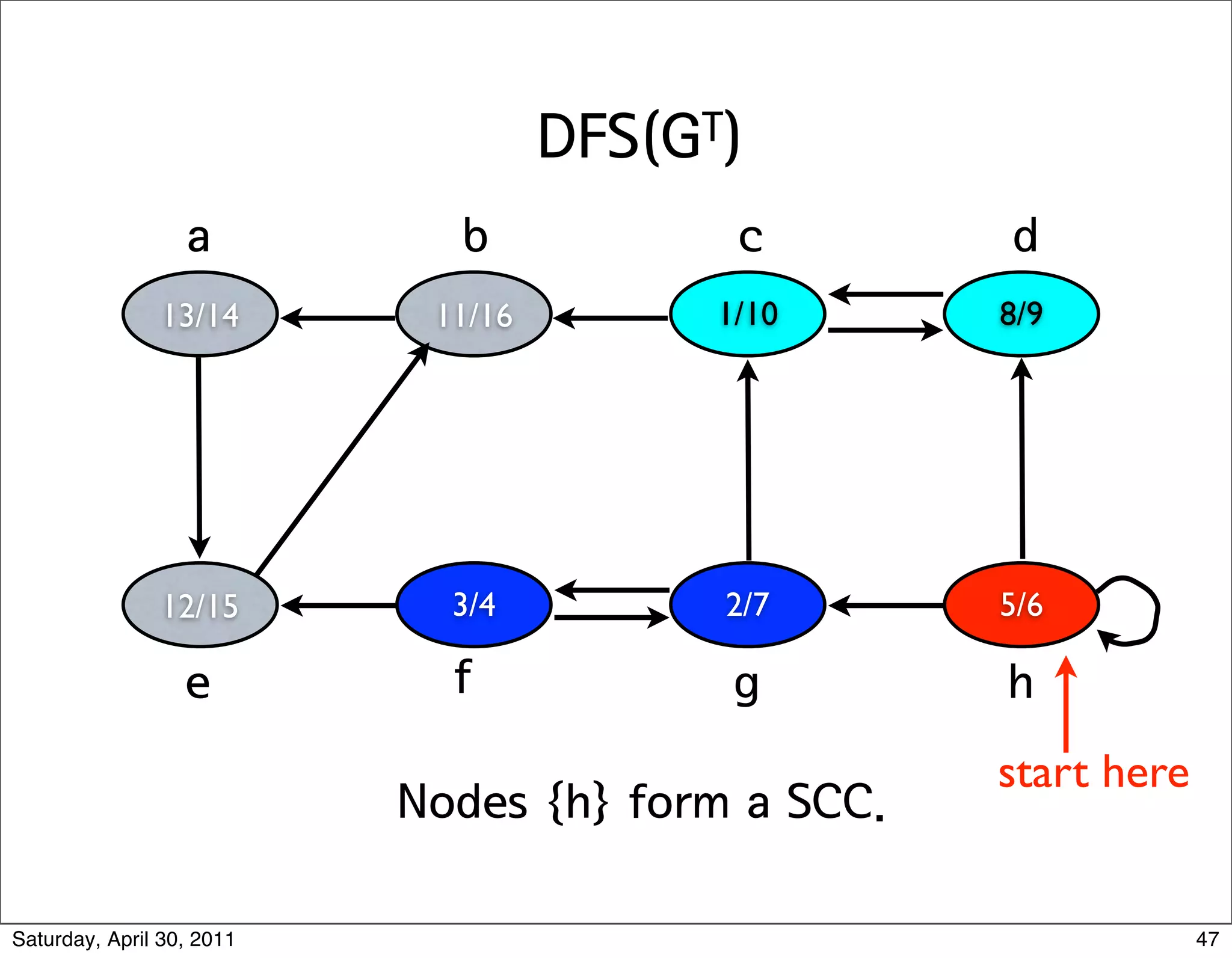
3) Depth-first search (DFS) which fully explores nodes reachable from the source before backtracking and exploring other branches.