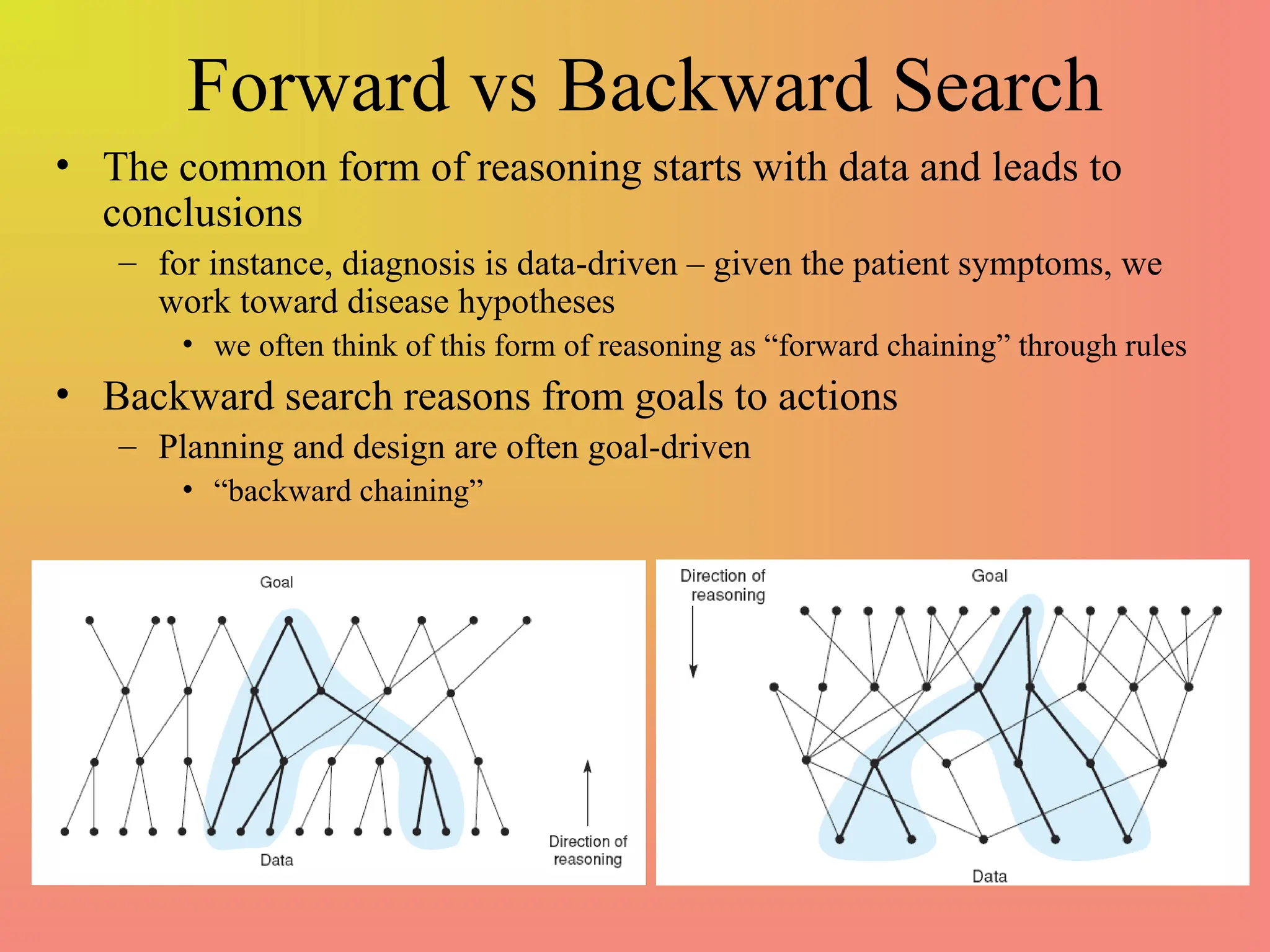
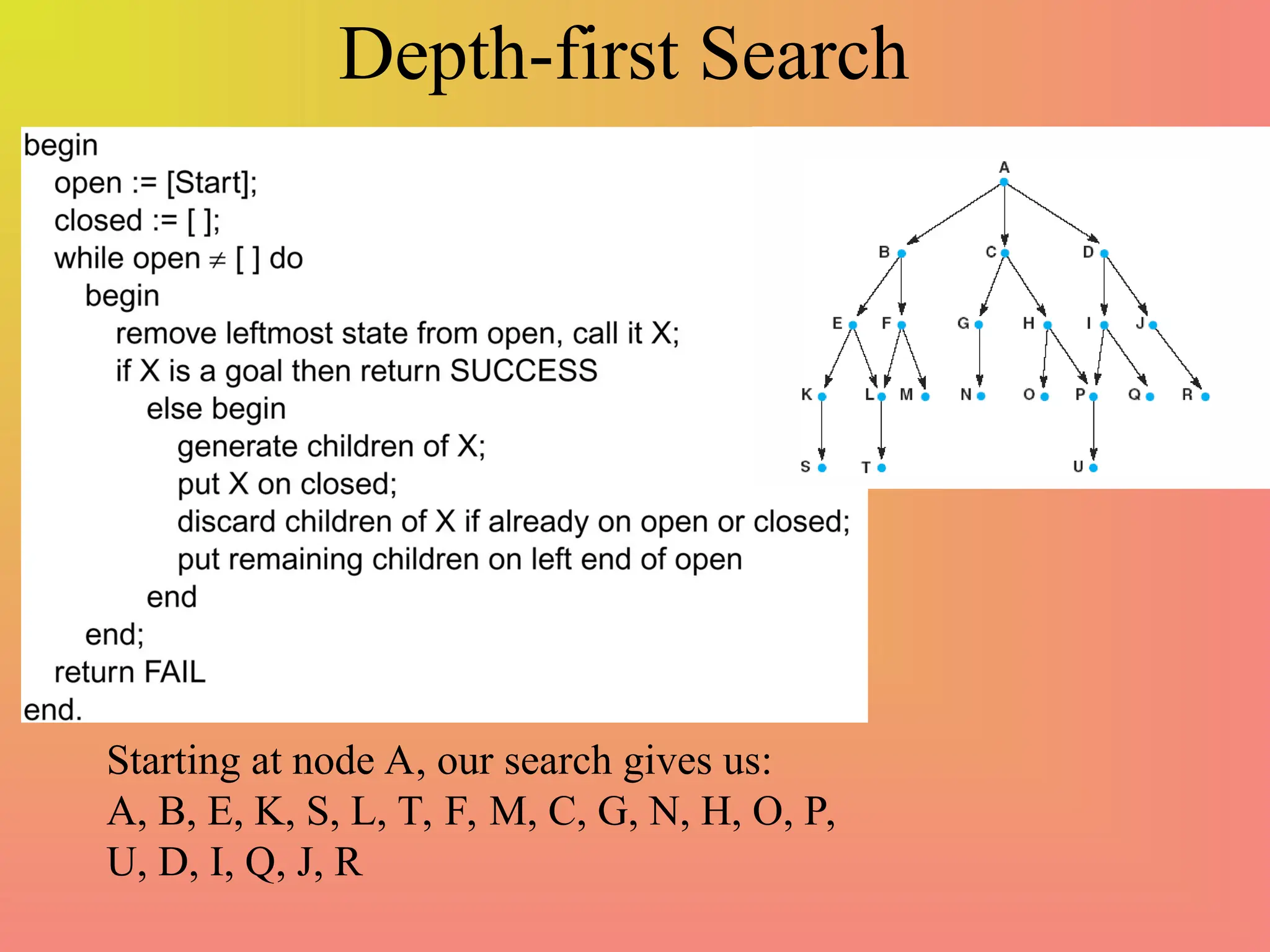
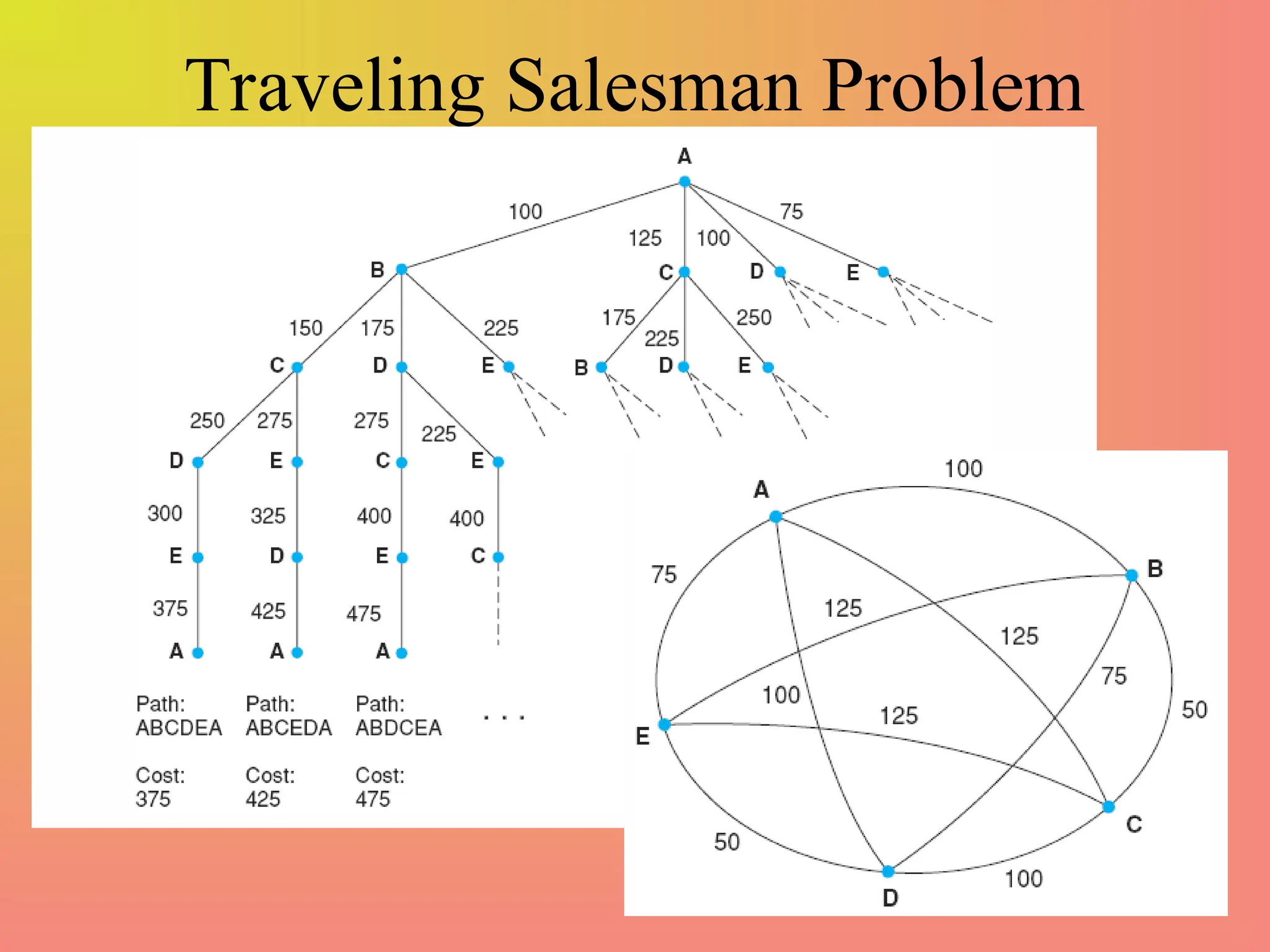
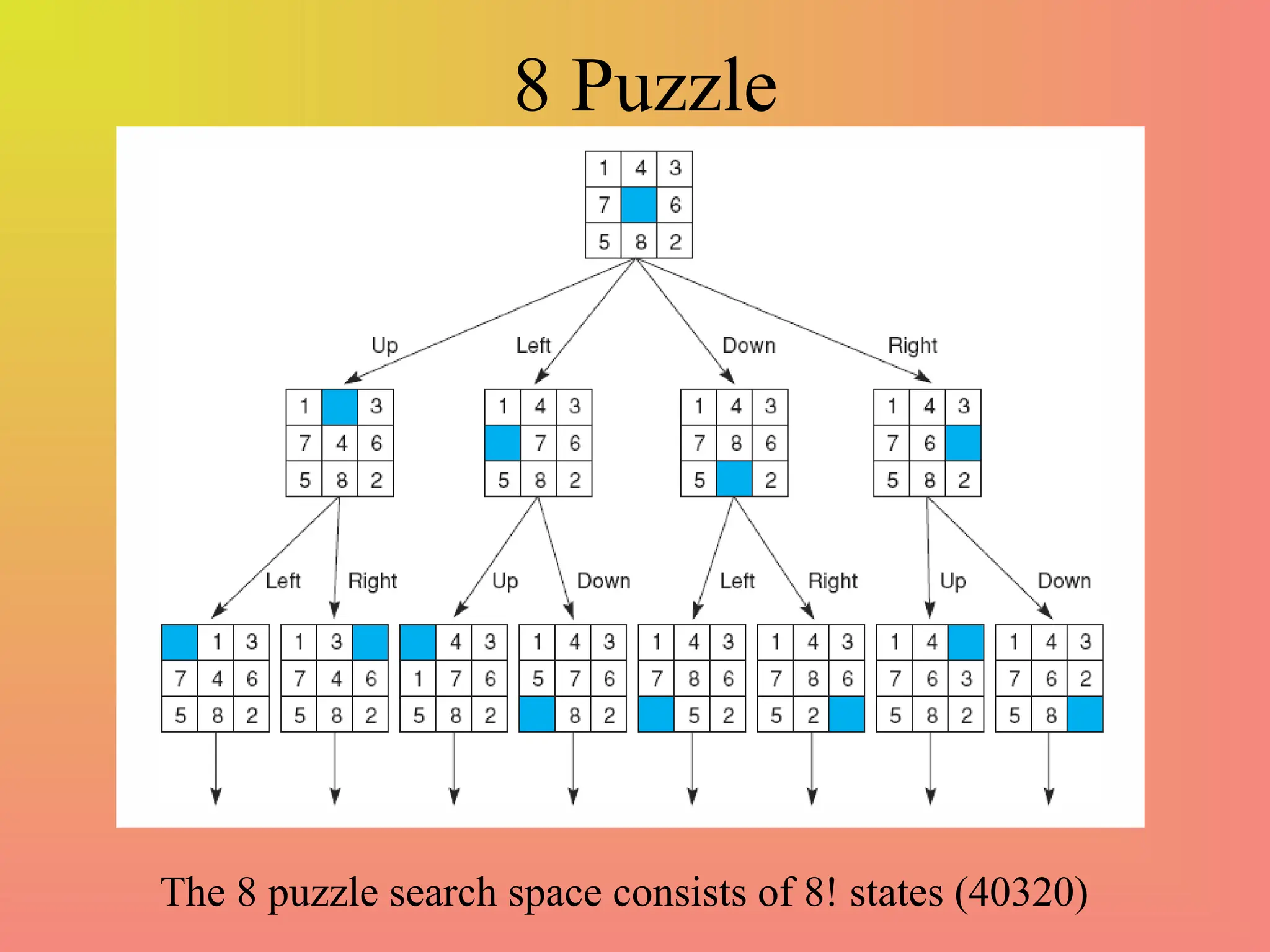
The document defines key concepts in artificial intelligence problem-solving, including state space, initial and goal states, and actions to transition between states. It presents examples such as the monkey and bananas problem, and the missionaries and cannibals problem, emphasizing the complexity and state space size in these problems. It also discusses search strategies, distinguishing between brute force and heuristic searches, and introduces concepts like forward and backward search reasoning.



![Search
• Given a problem expressed as a state space (whether
explicitly or implicitly)
– with operators/actions, an initial state and a goal state, how do
we find the sequence of operators needed to solve the problem?
– this requires search
• Formally, we define a search space as [N, A, S, GD]
– N = set of nodes or states of a graph
– A = set of arcs (edges) between nodes that correspond to the
steps in the problem (the legal actions or operators)
– S = a nonempty subset of N that represents start states
– GD = a nonempty subset of N that represents goal states
• Our problem becomes one of traversing the graph from a
node in S to a node in GD
– we can use any of the numerous graph traversal techniques for
this but in general, they divide into two categories:
• brute force – unguided search
• heuristic – guided search](https://image.slidesharecdn.com/ch3-241113052418-296d33f0/75/Ppt-on-chapter-3-made-by-students-in-python-5-2048.jpg)