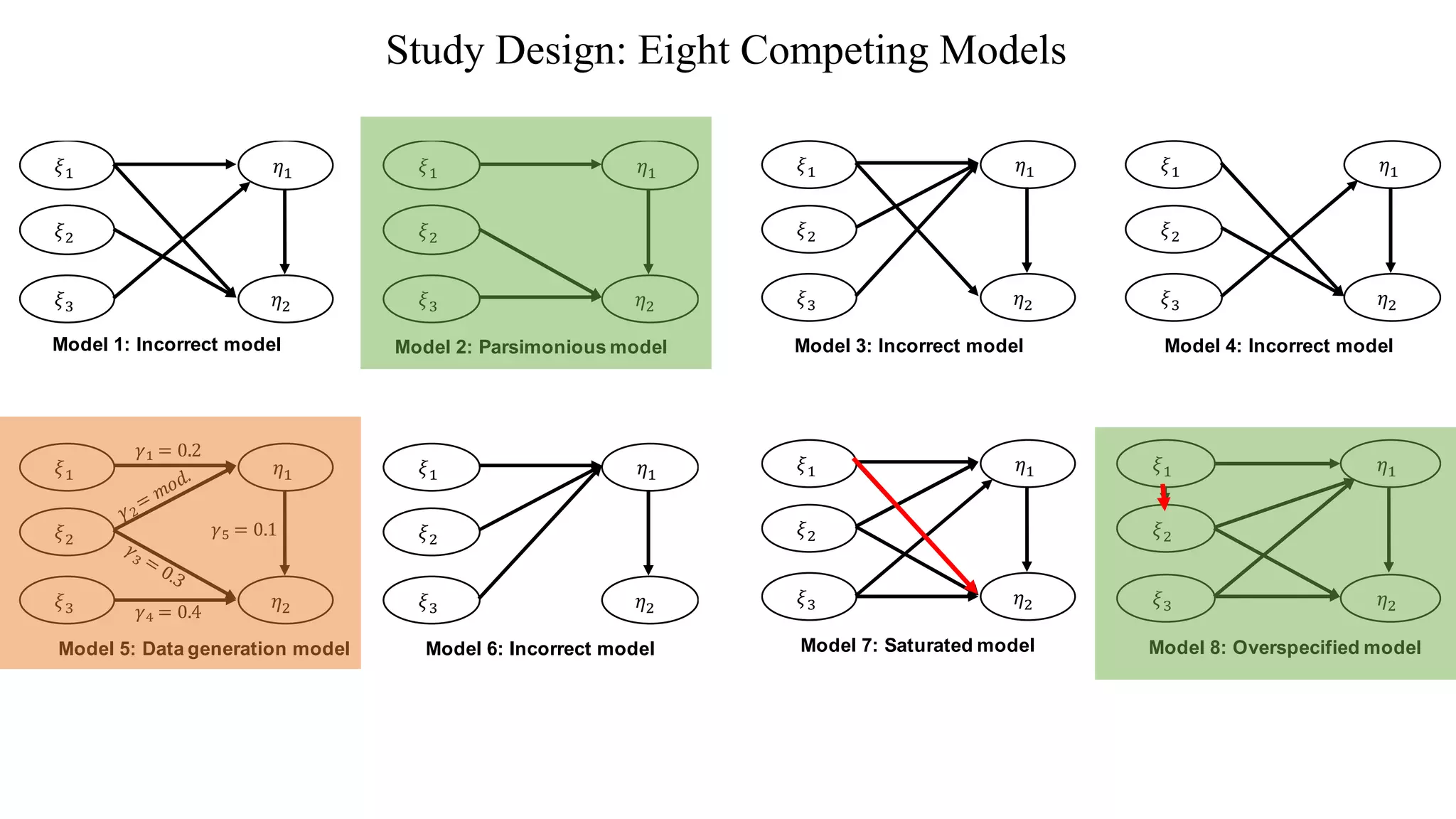
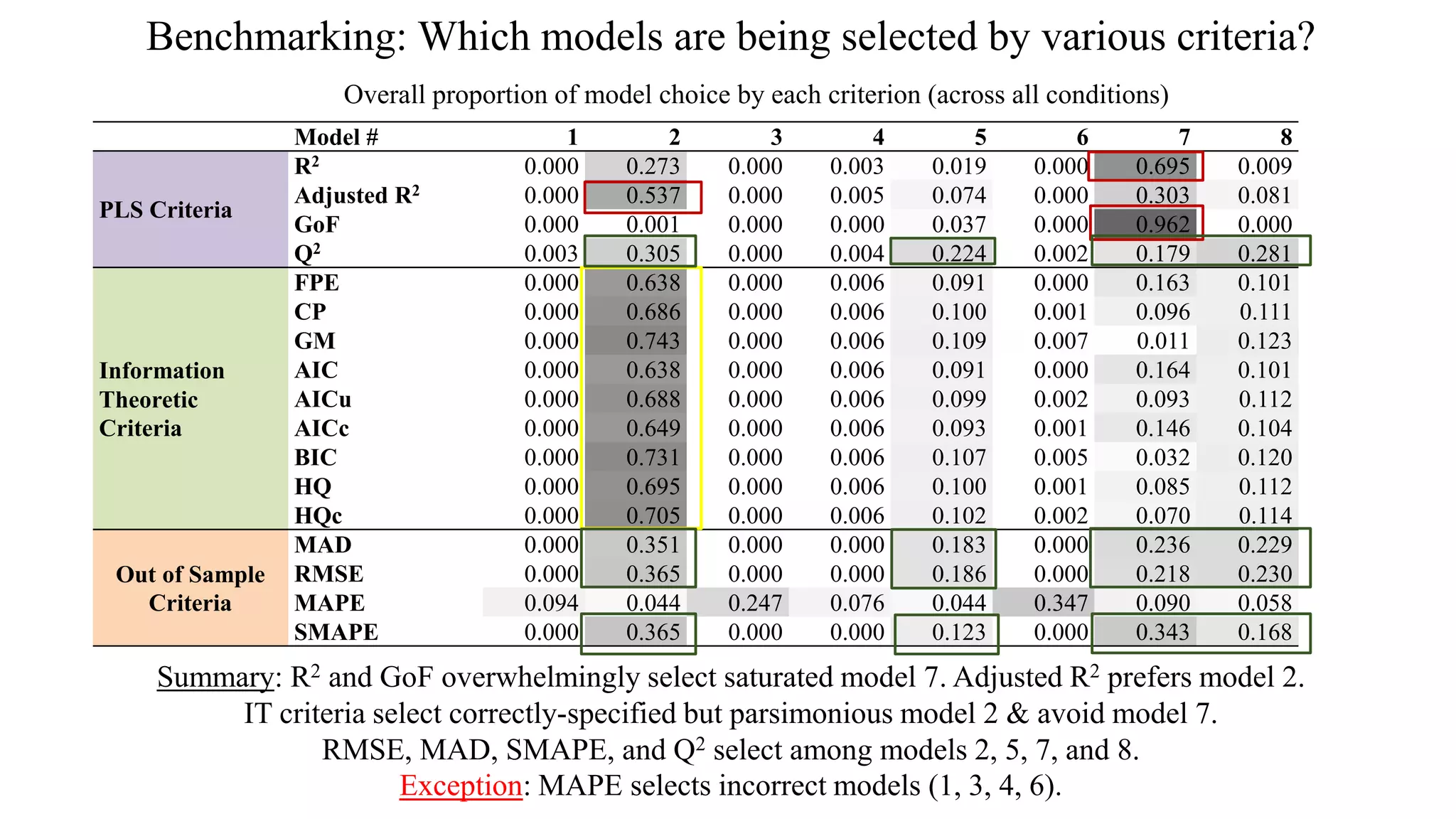
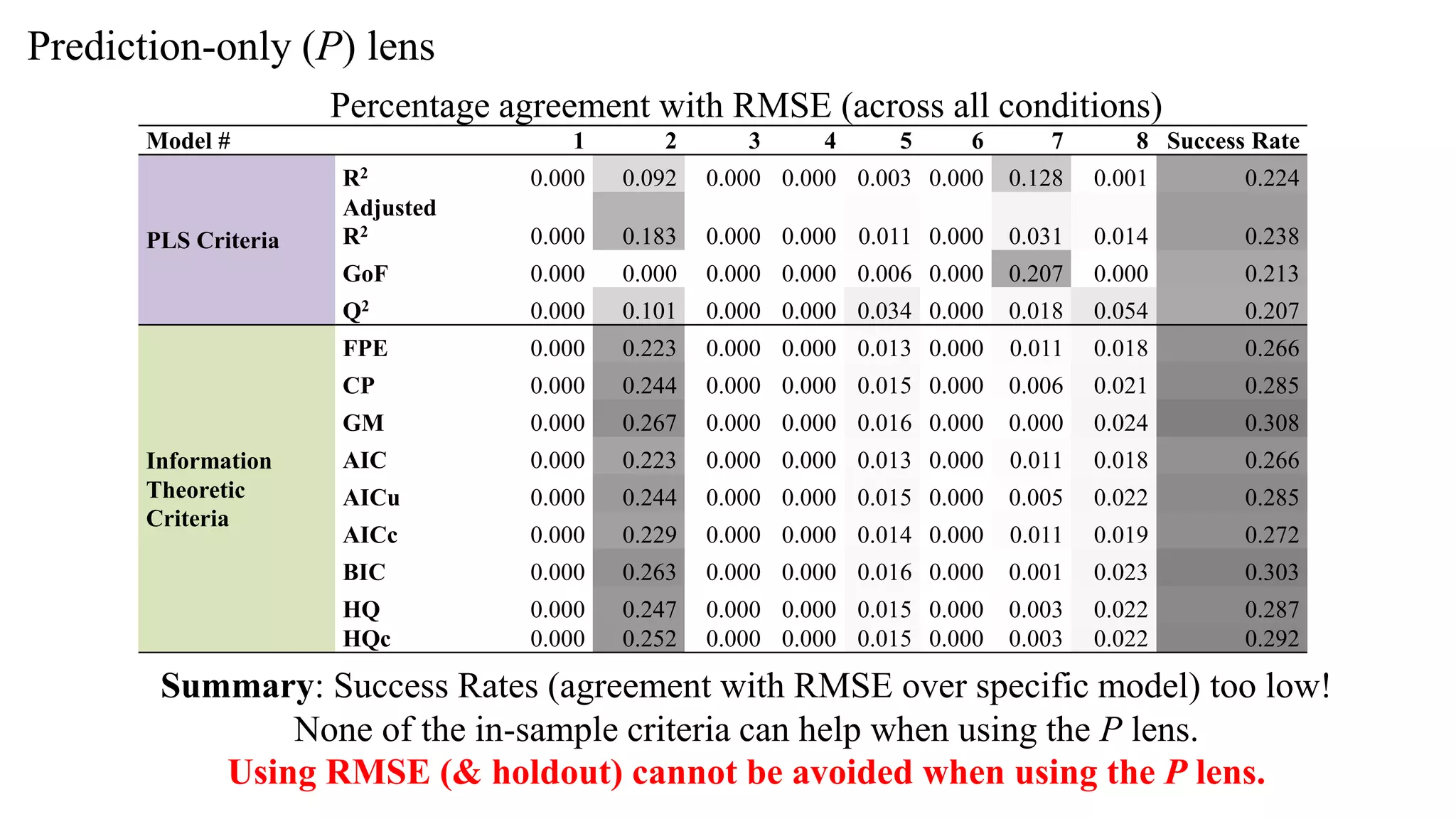
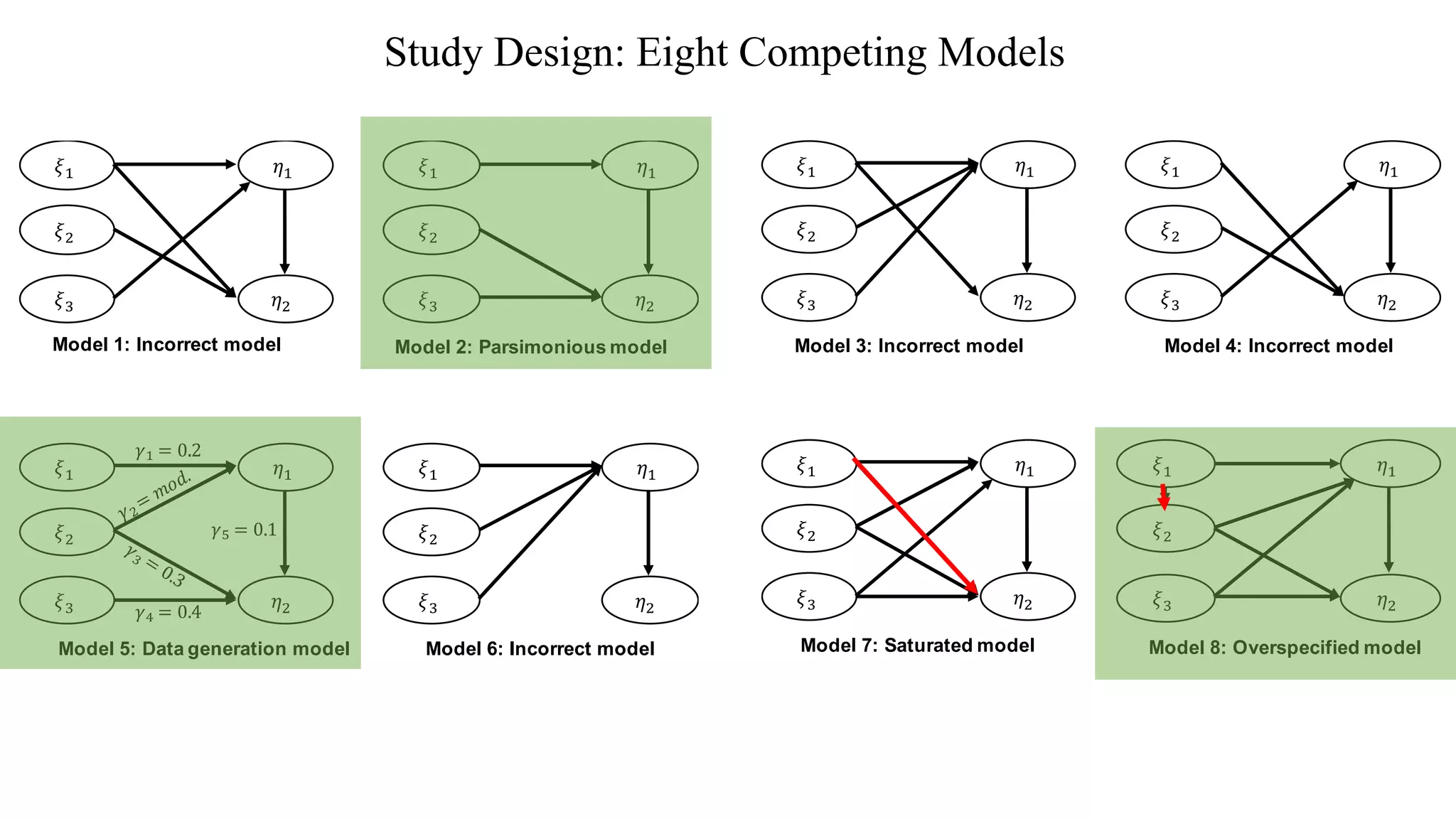
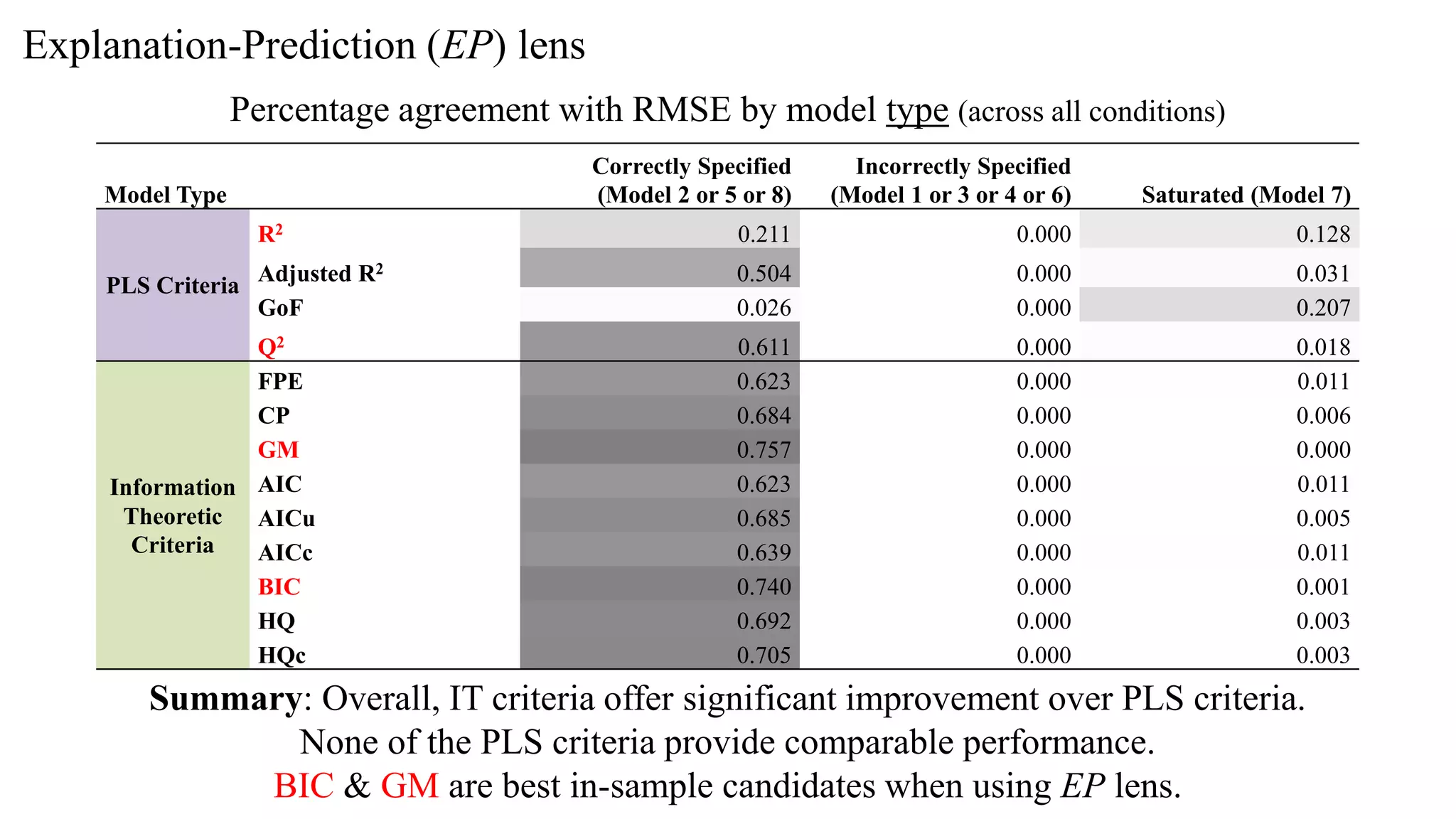
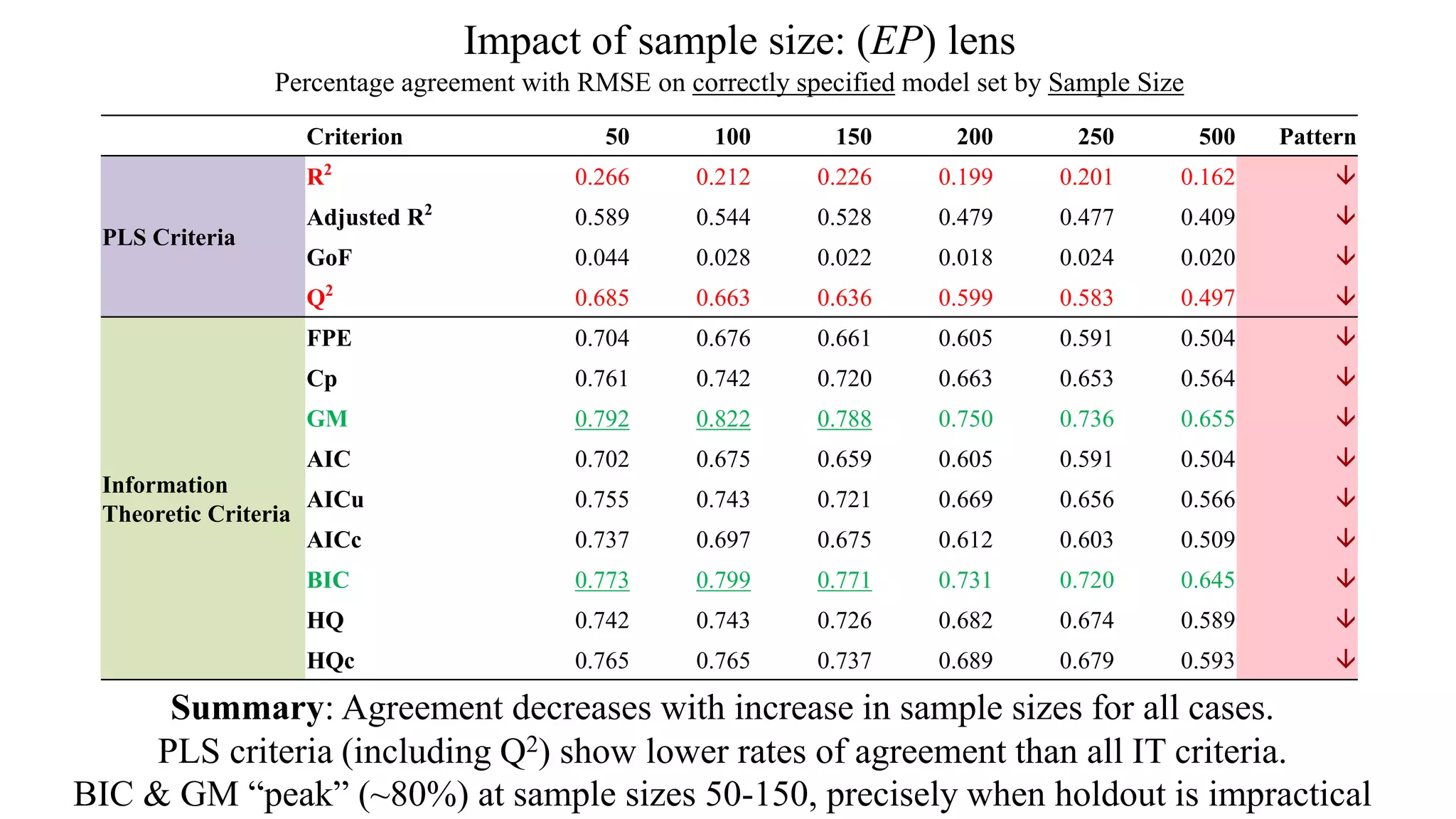
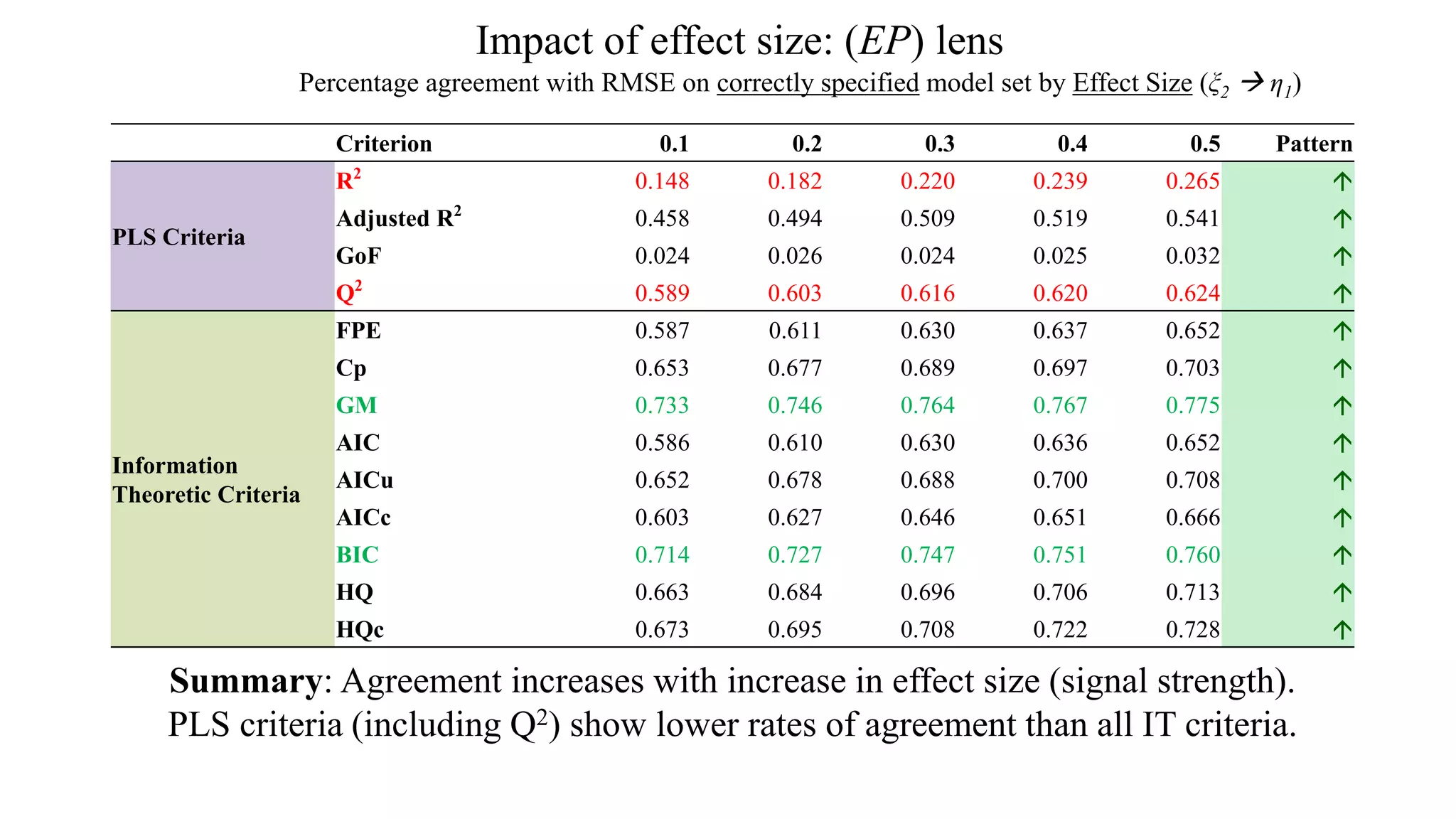
The document presents a study comparing various in-sample model selection criteria to out-of-sample criteria in predicting outcomes using partial least squares path modeling (PLS-PM). The study finds that information theoretic criteria like AIC, BIC, and HQ agree best with the gold standard RMSE criterion, correctly selecting predictive yet parsimonious models. Agreement rates decrease with larger sample sizes, where holdout samples are less critical. Information criteria outperform PLS criteria like R2 and Q2 at predictive model selection in PLS-PM.