Recursive Definitions in Discrete Mathmatcs.pptx

1
Recursive Definitions
Recursion is a principle closely related to
mathematical induction.
In a recursive definition, an object is defined in
terms of itself.
We can recursively define sequences, functions
and sets.

2
Recursively Defined Sequences
Example:
The sequence {an} of powers of 2 is given by
an = 2n for n = 0, 1, 2, … .
The same sequence can also be defined
recursively:
a0 = 1
an+1 = 2an for n = 0, 1, 2, …
Obviously, induction and recursion are similar
principles.

3
Recursively Defined Functions
We can use the following method to define a
function with the natural numbers as its domain:
1. Specify the value of the function at zero.
2. Give a rule for finding its value at any integer
from its values at smaller integers.
Such a definition is called recursive or inductive
definition.

4
Example:
f(0) = 3
f(n + 1) = 2f(n) + 3
f(0) = 3
f(1) = 2f(0) + 3 = 23 + 3 = 9
f(2) = 2f(1) + 3 = 29 + 3 = 21
f(3) = 2f(2) + 3 = 221 + 3 = 45
f(4) = 2f(3) + 3 = 245 + 3 = 93

5
How can we recursively define the factorial
function f(n) = n! ?
f(0) = 1
f(n + 1) = (n + 1)f(n)
f(0) = 1
f(1) = 1f(0) = 11 = 1
f(2) = 2f(1) = 21 = 2
f(3) = 3f(2) = 32 = 6
f(4) = 4f(3) = 46 = 24

6
A famous example: The Fibonacci numbers
f(0) = 0, f(1) = 1
f(n) = f(n – 1) + f(n - 2)
f(0) = 0
f(1) = 1
f(2) = f(1) + f(0) = 1 + 0 = 1
f(3) = f(2) + f(1) = 1 + 1 = 2
f(4) = f(3) + f(2) = 2 + 1 = 3
f(5) = f(4) + f(3) = 3 + 2 = 5
f(6) = f(5) + f(4) = 5 + 3 = 8

7
Recursively Defined Sets
If we want to recursively define a set, we need to
provide two things:
• an initial set of elements,
• rules for the construction of additional
elements from elements in the set.
Example: Let S be recursively defined by:
3  S
(x + y)  S if (x  S) and (y  S)
S is the set of positive integers divisible by 3.

8
Proof:
Let A be the set of all positive integers divisible by 3.
To show that A = S, we must show that
A  S and S  A.
Part I: To prove that A  S, we must show that
every positive integer divisible by 3 is in S.
We will use mathematical induction to show this.

9
Let P(n) be the statement “3n belongs to S”.
Basis step: P(1) is true, because 3 is in S.
Inductive step: To show:
If P(n) is true, then P(n + 1) is true.
Assume 3n is in S. Since 3n is in S and 3 is in S, it
follows from the recursive definition of S that
3n + 3 = 3(n + 1) is also in S.
Conclusion of Part I: A  S.

10
Part II: To show: S  A.
Basis step: To show:
All initial elements of S are in A. 3 is in A. True.
Inductive step: To show:
(x + y) is in A whenever x and y are in A.
If x and y are both in A, it follows that 3 | x and 3 | y.
As we already know, it follows that 3 | (x + y).
Conclusion of Part II: S  A.
Overall conclusion: A = S.

11
Another example:
The well-formed formulas of variables, numerals
and operators from {+, -, *, /, ^} are defined by:
x is a well-formed formula if x is a numeral or
variable.
(f + g), (f – g), (f * g), (f / g), (f ^ g) are well-formed
formulas if f and g are.

12
With this definition, we can construct formulas such
as:
(x – y)
((z / 3) – y)
((z / 3) – (6 + 5))
((z / (2 * 4)) – (6 + 5))

13
Recursive Algorithms
An algorithm is called recursive if it solves a problem
by reducing it to an instance of the same problem with
smaller input.
Example I: Recursive Euclidean Algorithm
procedure gcd(a, b: nonnegative integers with a < b)
if a = 0 then gcd(a, b) := b
else gcd(a, b) := gcd(b mod a, a)

14
Example II: Recursive Fibonacci Algorithm
procedure fibo(n: nonnegative integer)
if n = 0 then fibo(0) := 0
else if n = 1 then fibo(1) := 1
else fibo(n) := fibo(n – 1) + fibo(n – 2)

15
Recursive Fibonacci Evaluation:
f(4)
f(3)
f(2)
f(1) f(0)
f(1)
f(2)
f(1) f(0)

16
procedure iterative_fibo(n: nonnegative integer)
if n = 0 then y := 0
else
begin
x := 0
y := 1
for i := 1 to n-1
begin
z := x + y
x : = y
y := z
end
end {y is the n-th Fibonacci number}

17
For every recursive algorithm, there is an equivalent
iterative algorithm.
Recursive algorithms are often shorter, more
elegant, and easier to understand than their
iterative counterparts.
However, iterative algorithms are usually more
efficient in their use of space and time.

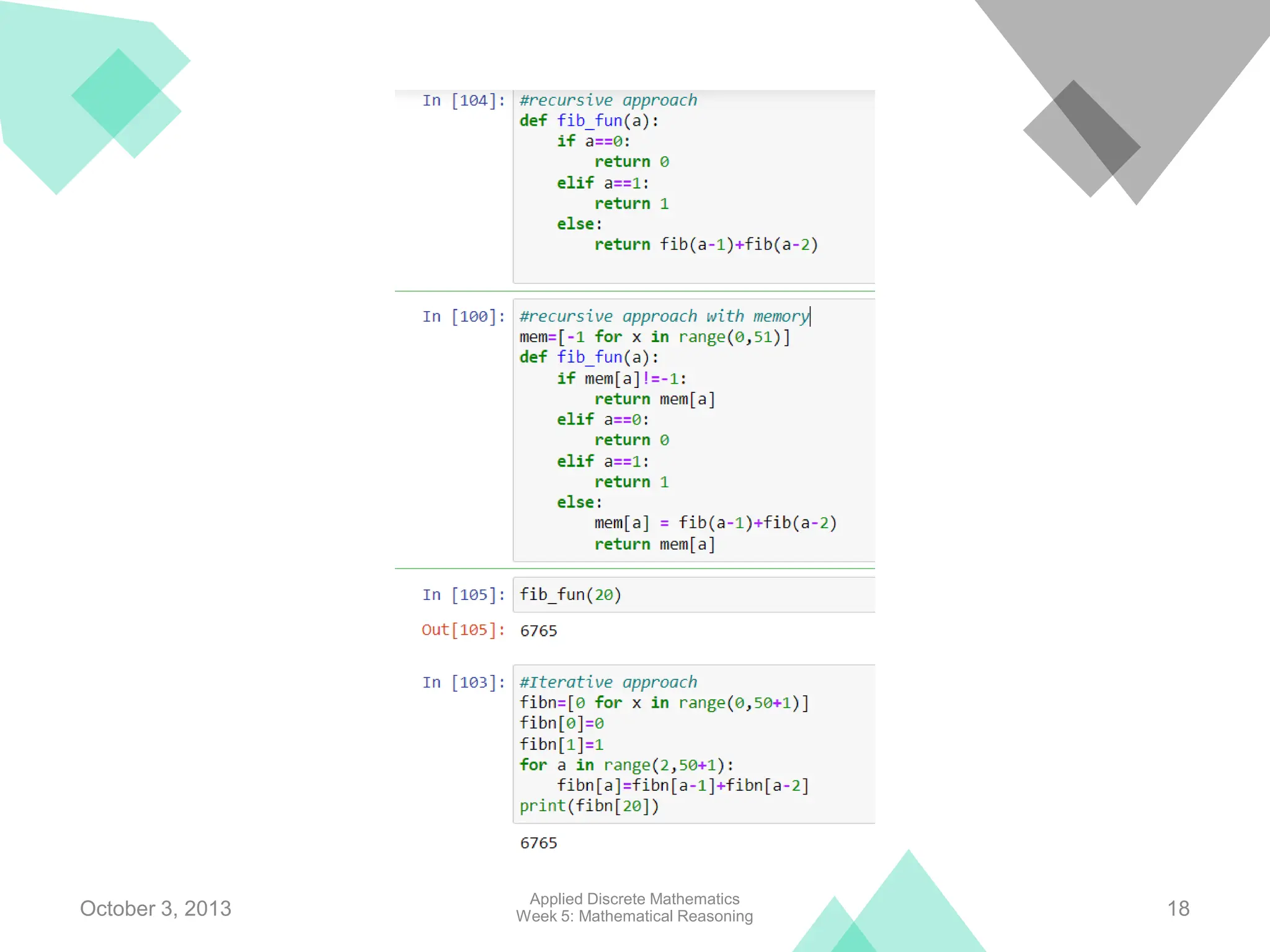
October 3, 2013
Applied Discrete Mathematics
Week 5: Mathematical Reasoning 18

Recursive Definitions in Discrete Mathmatcs.pptx

More Related Content

What's hot

Similar to Recursive Definitions in Discrete Mathmatcs.pptx

Recently uploaded

Recursive Definitions in Discrete Mathmatcs.pptx