This document presents an overview of ridge regression, lasso, and elastic net techniques within linear regression, highlighting their applications in estimation and prediction. It discusses the importance of regularization for improving prediction accuracy in the presence of multicollinearity among predictors and compares the strengths and weaknesses of each method. Practical examples, such as leukemia classification, illustrate the challenges and solutions associated with these regression techniques.


![2/13/2014
Ridge Regression, LASSO and Elastic Net
Quality of an estimator
+
T
0
x = y
, the difference between the actual response and the model prediction
2
2
])
T
0
)
T
0
x
T
0
T
0
x (raV + )
0
T
0
x
y([E = ) 0 x(EPE
x(E +
2
2
= ) 0 x(EPE
x( sa iB[ +
2
.
0
x
in estimating
T
T
0
x
)
= ) 0 x(EPE
T
0
x
T
0
0
x(E = )
T
0
x( sa iB
· The second and third terms make up the mean squared error of
0
x
Where
] 0 x = x| )
0
0
· Prediction error at
,
is the true value and
) 1 , 0(
Suppose
.
· How to estimate prediction error?
4/42
file:///Users/ytsun/elasticnet/index.html#42
4/42](https://image.slidesharecdn.com/ridgeregressionlassoandelasticnet-140213173630-phpapp02/75/Ridge-regression-lasso-and-elastic-net-4-2048.jpg)


![2/13/2014
Ridge Regression, LASSO and Elastic Net
Quality of an estimator
· Mean squared error of the estimator
2
] )
)
0
(raV + )
([ E = )
2
(ESM
( sa iB = )
(ESM
· A biased estimator may achieve smaller MSE than an unbiased estimator
· useful when our goal is to understand the relationship instead of prediction
7/42
file:///Users/ytsun/elasticnet/index.html#42
7/42](https://image.slidesharecdn.com/ridgeregressionlassoandelasticnet-140213173630-phpapp02/75/Ridge-regression-lasso-and-elastic-net-7-2048.jpg)








![2/13/2014
Ridge Regression, LASSO and Elastic Net
Ridge Regression
#cos tnn prmtr
hoe uig aaee
rdemdl=l.ig( ~.-1 d lmd =sq0 1,01)
ig.oe
mrdey
, , aba
e(, 0 .)
lmd.p =rdemdllmd[hc.i(ig.oe$C)
abaot
ig.oe$abawihmnrdemdlGV]
#rdergeso (hikcefcet)
ig ersin srn ofiins
ce(mrdey~.-1 d lmd =lmd.p)
ofl.ig(
, , aba
abaot)
#
#
x
1
x
2
x
3
# 017 010 015
# .71 .92 .28
17/42
file:///Users/ytsun/elasticnet/index.html#42
17/42](https://image.slidesharecdn.com/ridgeregressionlassoandelasticnet-140213173630-phpapp02/75/Ridge-regression-lasso-and-elastic-net-17-2048.jpg)
![2/13/2014
Ridge Regression, LASSO and Elastic Net
Approximately multicollinear
· show that ridge regreesion correct coefficient signs and reduce mean squared error
x =x +x +00 *romn 0 1
3
1
2
.5
nr(, , )
d=dt.rm( =y x =x,x =x,x =x)
aafaey
, 1
1 2
2 3
3
dtan=d140 ]
.ri
[:0,
dts =d4150 ]
.et
[0:0,
18/42
file:///Users/ytsun/elasticnet/index.html#42
18/42](https://image.slidesharecdn.com/ridgeregressionlassoandelasticnet-140213173630-phpapp02/75/Ridge-regression-lasso-and-elastic-net-18-2048.jpg)
![2/13/2014
Ridge Regression, LASSO and Elastic Net
OLS
ostan=l( ~.-1 dtan
l.ri
my
, .ri)
ce(l.ri)
ofostan
#
#
x
1
x
2
x
3
# -.74-.52 063
# 036 032
.89
#peito err
rdcin ros
sm(.ety-peitostan nwaa=dts)^)
u(dts$
rdc(l.ri, edt
.et)2
# []3.3
# 1 75
19/42
file:///Users/ytsun/elasticnet/index.html#42
19/42](https://image.slidesharecdn.com/ridgeregressionlassoandelasticnet-140213173630-phpapp02/75/Ridge-regression-lasso-and-elastic-net-19-2048.jpg)
![2/13/2014
Ridge Regression, LASSO and Elastic Net
Ridge Regression
#cos tnn prmtrfrrdergeso
hoe uig aaee o ig ersin
rdetan=l.ig( ~.-1 dtan lmd =sq0 1,01)
ig.ri
mrdey
, .ri, aba
e(, 0 .)
lmd.p =rdetanlmd[hc.i(ig.ri$C)
abaot
ig.ri$abawihmnrdetanGV]
rdemdl=l.ig( ~.-1 dtan lmd =lmd.p)
ig.oe
mrdey
, .ri, aba
abaot
ce(ig.oe) #cretsgs
ofrdemdl
orc in
#
#
x
1
x
2
x
3
# 011 013 014
# .73 .96 .30
ces=ce(ig.oe)
of
ofrdemdl
sm(.ety-a.arxdts[ -] %%mti(of,3 1)2
u(dts$
smti(.et, 1) * arxces , )^)
# []3.7
# 1 68
20/42
file:///Users/ytsun/elasticnet/index.html#42
20/42](https://image.slidesharecdn.com/ridgeregressionlassoandelasticnet-140213173630-phpapp02/75/Ridge-regression-lasso-and-elastic-net-20-2048.jpg)



![2/13/2014
Ridge Regression, LASSO and Elastic Net
LARS Path
S LO
] 1 , 0[
s ,1
s
1
. t. s
2
2
X
Y
n im
24/42
file:///Users/ytsun/elasticnet/index.html#42
24/42](https://image.slidesharecdn.com/ridgeregressionlassoandelasticnet-140213173630-phpapp02/75/Ridge-regression-lasso-and-elastic-net-24-2048.jpg)
![2/13/2014
Ridge Regression, LASSO and Elastic Net
parsimonious model
lbayMS)
irr(AS
n=2
0
#bt i sas
ea s pre
bt =mti((,15 0 0 2 0 0 0,8 1
ea
arxc3 ., , , , , , ) , )
p=lnt(ea
eghbt)
ro=03
h
.
cr =mti(,p p
or
arx0 , )
fr( i sqp){
o i n e()
fr( i sqp){
o j n e()
cr[,j =roasi-j
ori ]
h^b(
)
}
}
X=mromn m =rp0 p,Sga=cr)
vnr(, u
e(, ) im
or
y=X%%bt +3*romn 0 1
* ea
nr(, , )
d=a.aafaecidy X)
sdt.rm(bn(, )
clae()=c"" pse(x,sqp)
onmsd
(y, at0"" e())
25/42
file:///Users/ytsun/elasticnet/index.html#42
25/42](https://image.slidesharecdn.com/ridgeregressionlassoandelasticnet-140213173630-phpapp02/75/Ridge-regression-lasso-and-elastic-net-25-2048.jpg)
![2/13/2014
Ridge Regression, LASSO and Elastic Net
OLS
nsm=10
.i
0
me=rp0 nsm
s
e(, .i)
fr( i sqnsm){
o i n e(.i)
X=mromn m =rp0 p,Sga=cr)
vnr(, u
e(, ) im
or
y=X%%bt +3*romn 0 1
* ea
nr(, , )
d=a.aafaecidy X)
sdt.rm(bn(, )
clae()=c"" pse(x,sqp)
onmsd
(y, at0"" e())
#ftOSwtotitret
i L ihu necp
osmdl=l( ~.-1 d
l.oe
my
, )
mei =sm(ofosmdl -bt)2
s[]
u(ce(l.oe)
ea^)
}
mda(s)
einme
# []63
# 1 .2
26/42
file:///Users/ytsun/elasticnet/index.html#42
26/42](https://image.slidesharecdn.com/ridgeregressionlassoandelasticnet-140213173630-phpapp02/75/Ridge-regression-lasso-and-elastic-net-26-2048.jpg)
![2/13/2014
Ridge Regression, LASSO and Elastic Net
Ridge Regression
nsm=10
.i
0
me=rp0 nsm
s
e(, .i)
fr( i sqnsm){
o i n e(.i)
X=mromn m =rp0 p,Sga=cr)
vnr(, u
e(, ) im
or
y=X%%bt +3*romn 0 1
* ea
nr(, , )
d=a.aafaecidy X)
sdt.rm(bn(, )
clae()=c"" pse(x,sqp)
onmsd
(y, at0"" e())
rdec =l.ig( ~.-1 d lmd =sq0 1,01)
ig.v
mrdey
, , aba
e(, 0 .)
lmd.p =rdec$abawihmnrdec$C)
abaot
ig.vlmd[hc.i(ig.vGV]
#ftrdergeso wtotitret
i ig ersin ihu necp
rdemdl=l.ig( ~.-1 d lmd =lmd.p)
ig.oe
mrdey
, , aba
abaot
mei =sm(ofrdemdl -bt)2
s[]
u(ce(ig.oe)
ea^)
}
mda(s)
einme
# []404
# 1 .7
27/42
file:///Users/ytsun/elasticnet/index.html#42
27/42](https://image.slidesharecdn.com/ridgeregressionlassoandelasticnet-140213173630-phpapp02/75/Ridge-regression-lasso-and-elastic-net-27-2048.jpg)
![2/13/2014
Ridge Regression, LASSO and Elastic Net
LASSO
lbayeatce)
irr(lsint
nsm=10
.i
0
me=rp0 nsm
s
e(, .i)
fr( i sqnsm){
o i n e(.i)
X=mromn m =rp0 p,Sga=cr)
vnr(, u
e(, ) im
or
y=X%%bt +3*romn 0 1
* ea
nr(, , )
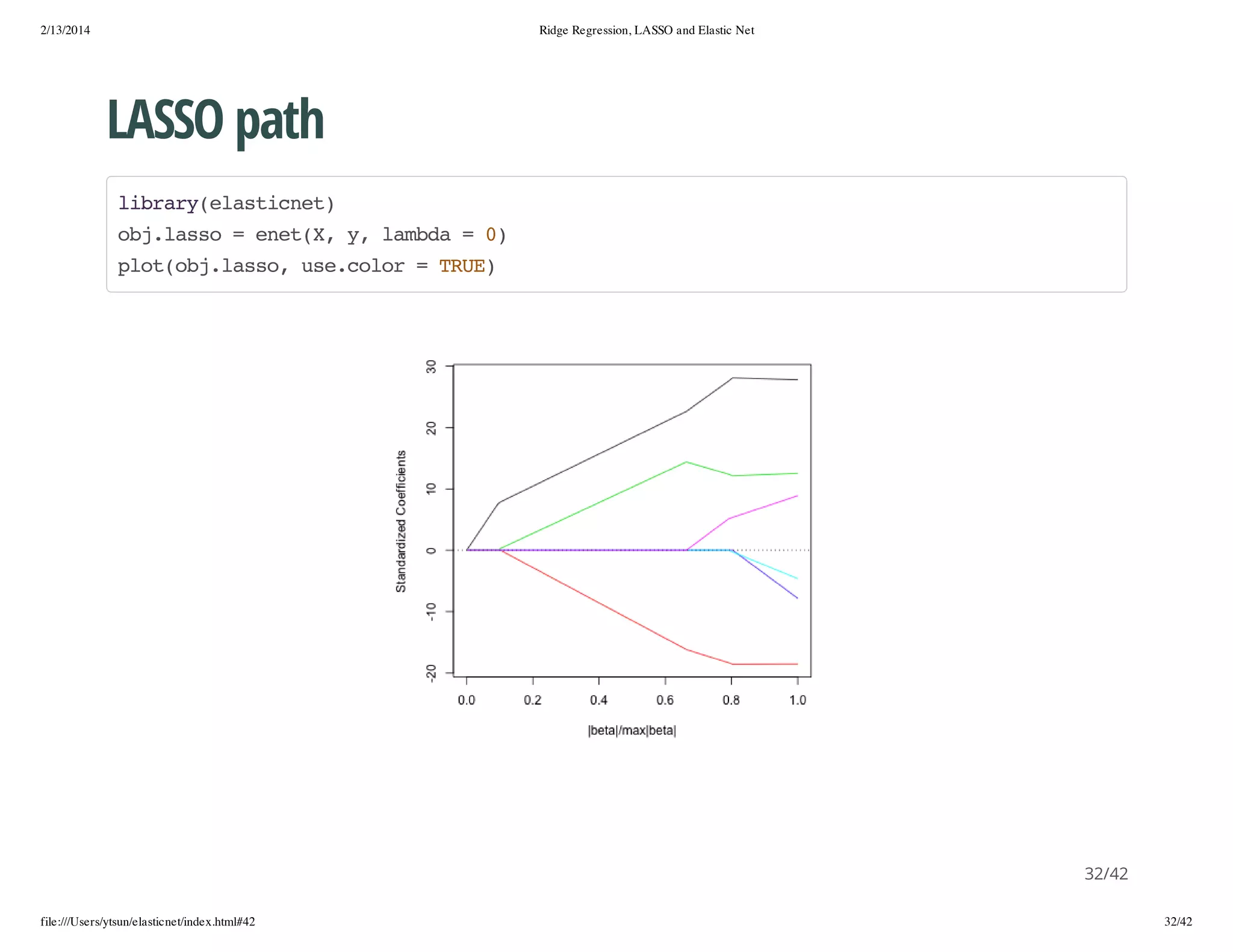
ojc =c.ntX y lmd =0 s=sq01 1 lnt =10,po.t=FLE
b.v
vee(, , aba
,
e(., , egh
0) lti
AS,
md ="rcin,tae=FLE mxses=8)
oe
fato" rc
AS, a.tp
0
sot=ojc$[hc.i(b.vc)
.p
b.vswihmnojc$v]
lsomdl=ee(,y lmd =0 itret=FLE
as.oe
ntX , aba
, necp
AS)
ces=peitlsomdl s=sot tp ="ofiins,md ="rcin)
of
rdc(as.oe,
.p, ye
cefcet" oe
fato"
mei =sm(of$ofiins-bt)2
s[]
u(cescefcet
ea^)
}
mda(s)
einme
# []333
# 1 .9
28/42
file:///Users/ytsun/elasticnet/index.html#42
28/42](https://image.slidesharecdn.com/ridgeregressionlassoandelasticnet-140213173630-phpapp02/75/Ridge-regression-lasso-and-elastic-net-28-2048.jpg)







![2/13/2014
Ridge Regression, LASSO and Elastic Net
Exercise 1: simulated data
bt =mti((e(,1) rp0 2),4,1
ea
arxcrp3 5, e(, 5) 0 )
sga=1
im
5
n=50
0
z =mti(nr(,0 1,n 1
1
arxromn , ) , )
z =mti(nr(,0 1,n 1
2
arxromn , ) , )
z =mti(nr(,0 1,n 1
3
arxromn , ) , )
X =z %%mti(e(,5,1 5 +00 *mti(nr( *5,n 5
1
1 * arxrp1 ) , )
.1
arxromn
) , )
X =z %%mti(e(,5,1 5 +00 *mti(nr( *5,n 5
2
2 * arxrp1 ) , )
.1
arxromn
) , )
X =z %%mti(e(,5,1 5 +00 *mti(nr( *5,n 5
3
3 * arxrp1 ) , )
.1
arxromn
) , )
X =mti(nr( *2,0 1,n 2)
4
arxromn
5 , ) , 5
X=cidX,X,X,X)
bn(1 2 3 4
Y=X%%bt +sga*romn 0 1
* ea
im
nr(, , )
Ytan=Y140
.ri
[:0]
Xtan=X140 ]
.ri
[:0,
Yts =Y4050
.et
[0:0]
Xts =X4050 ]
.et
[0:0,
39/42
file:///Users/ytsun/elasticnet/index.html#42
39/42](https://image.slidesharecdn.com/ridgeregressionlassoandelasticnet-140213173630-phpapp02/75/Ridge-regression-lasso-and-elastic-net-39-2048.jpg)

![2/13/2014
Ridge Regression, LASSO and Elastic Net
Exercise 2: Diabetes
· x a matrix with 10 columns
· y a numeric vector (442 rows)
· x2 a matrix with 64 columns
lbayeatce)
irr(lsint
dt(ibts
aadaee)
clae(ibts
onmsdaee)
# []"" "" "2
# 1 x
y
x"
41/42
file:///Users/ytsun/elasticnet/index.html#42
41/42](https://image.slidesharecdn.com/ridgeregressionlassoandelasticnet-140213173630-phpapp02/75/Ridge-regression-lasso-and-elastic-net-41-2048.jpg)
