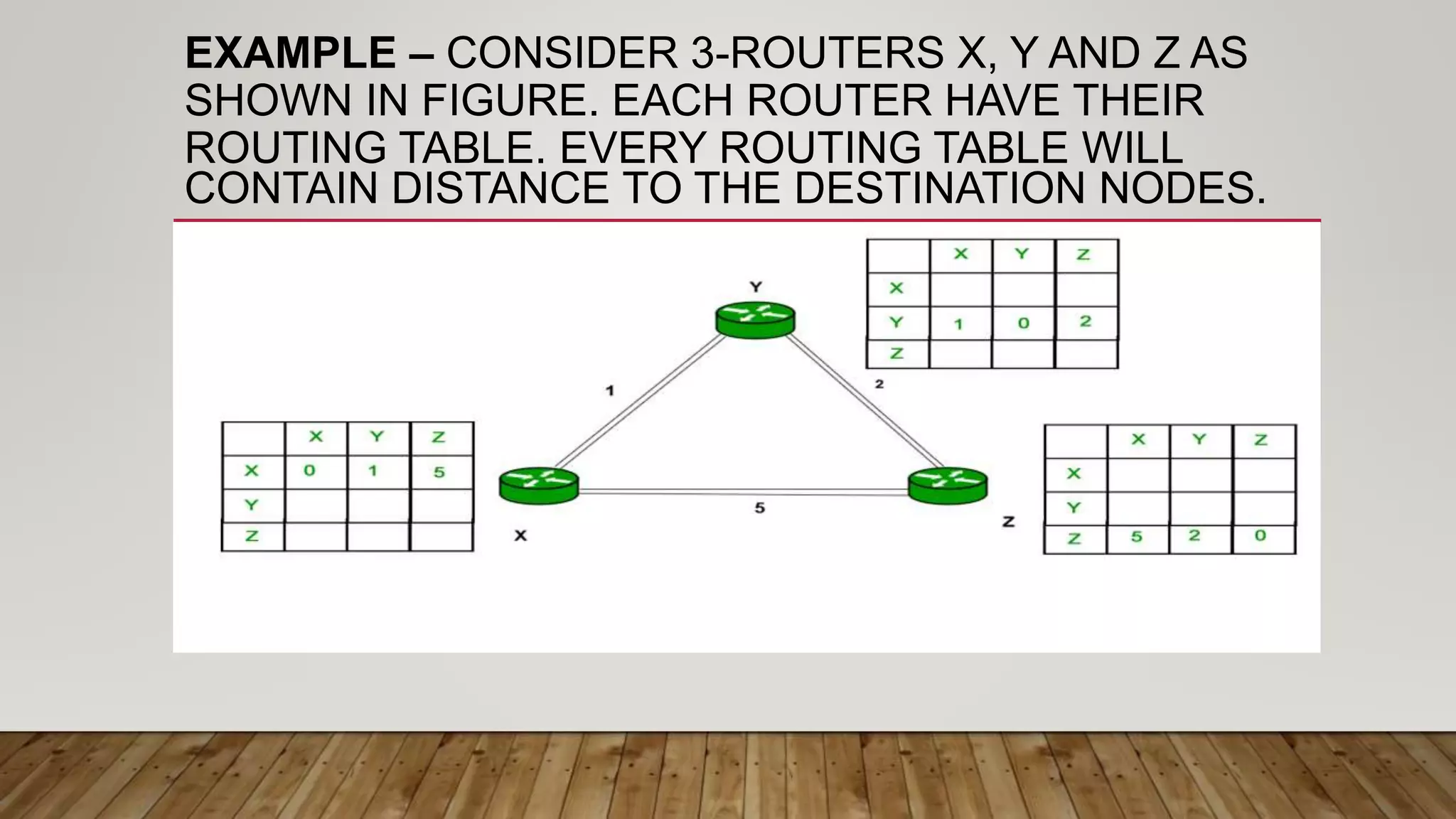
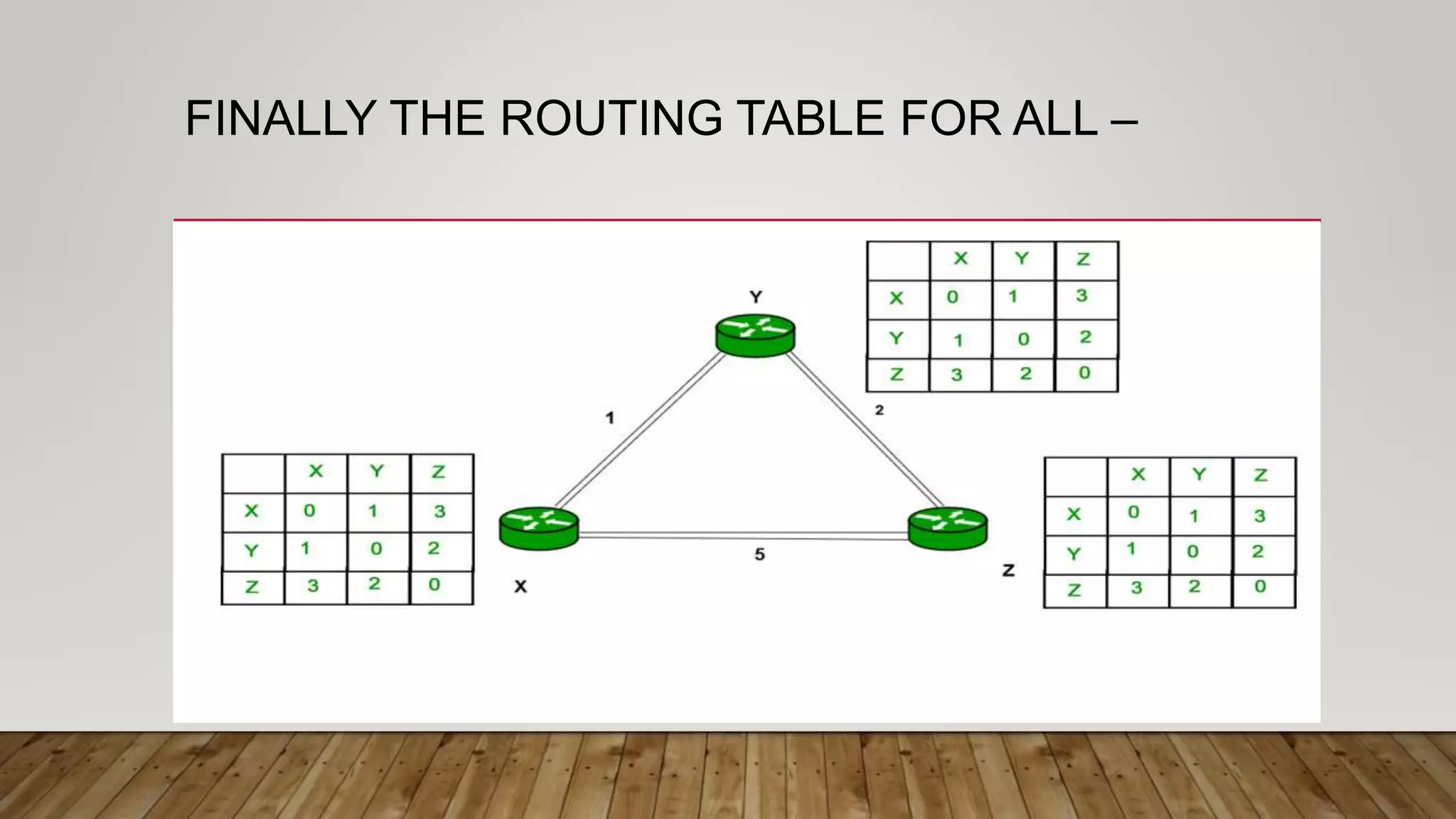
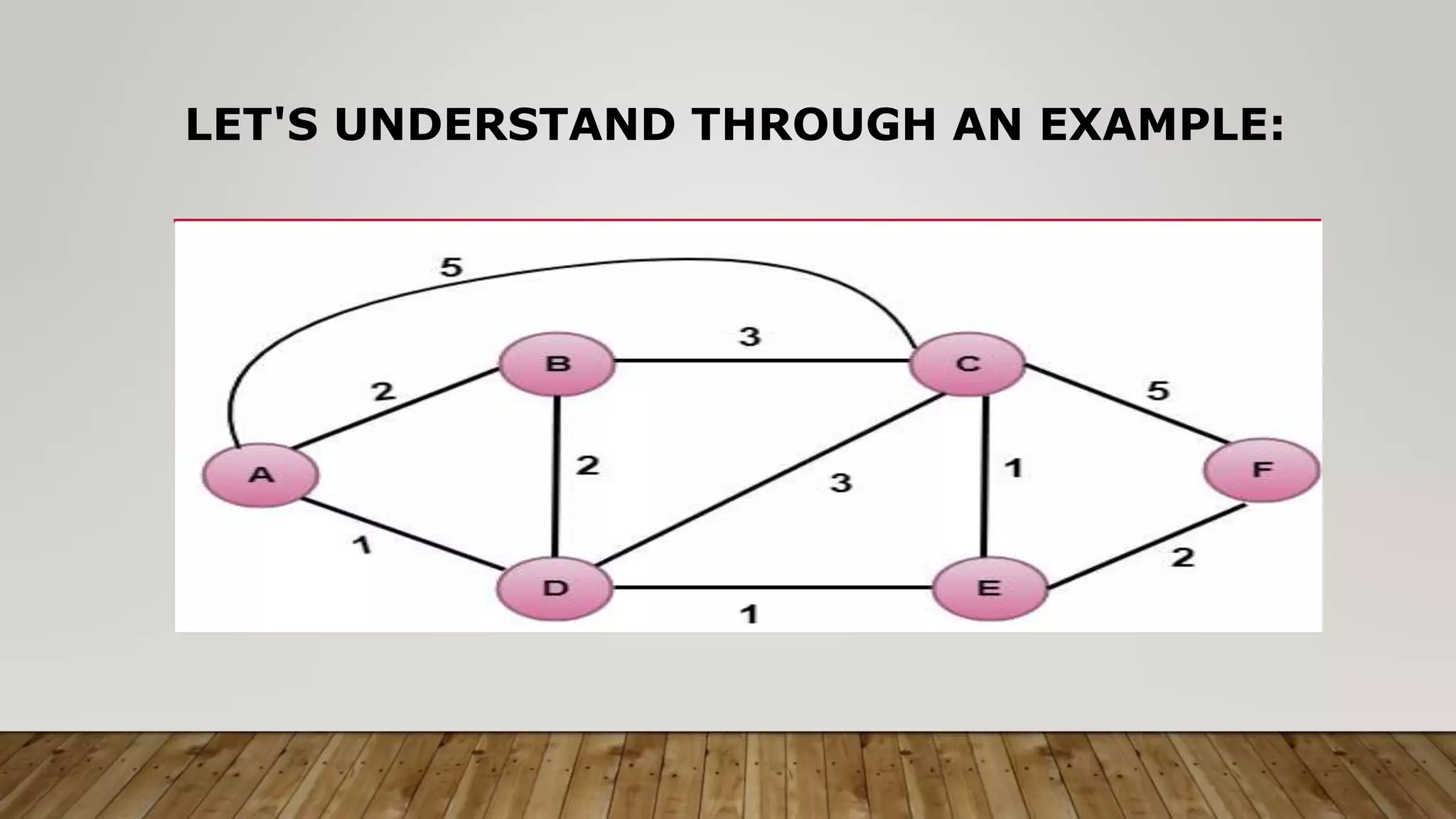
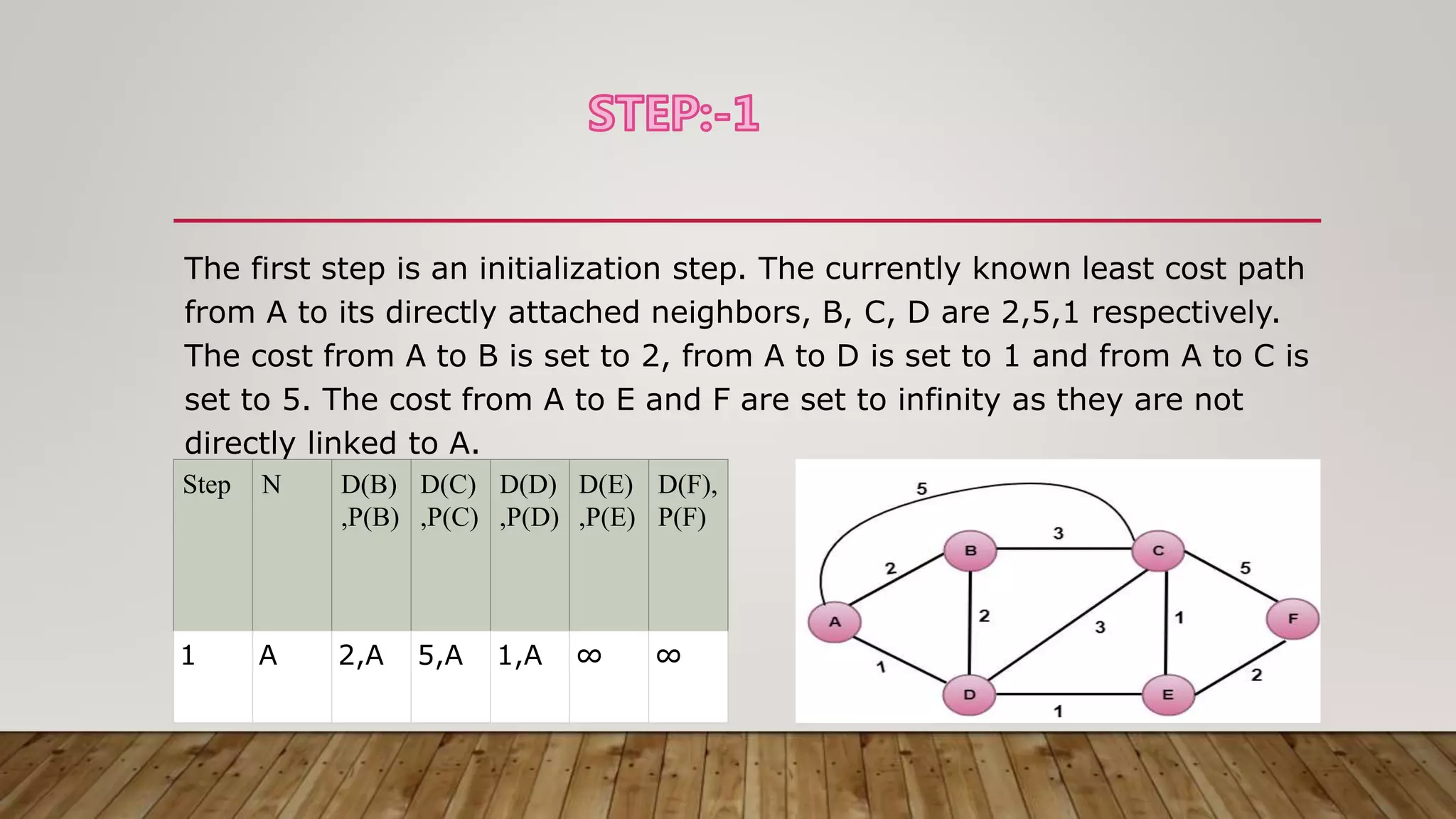
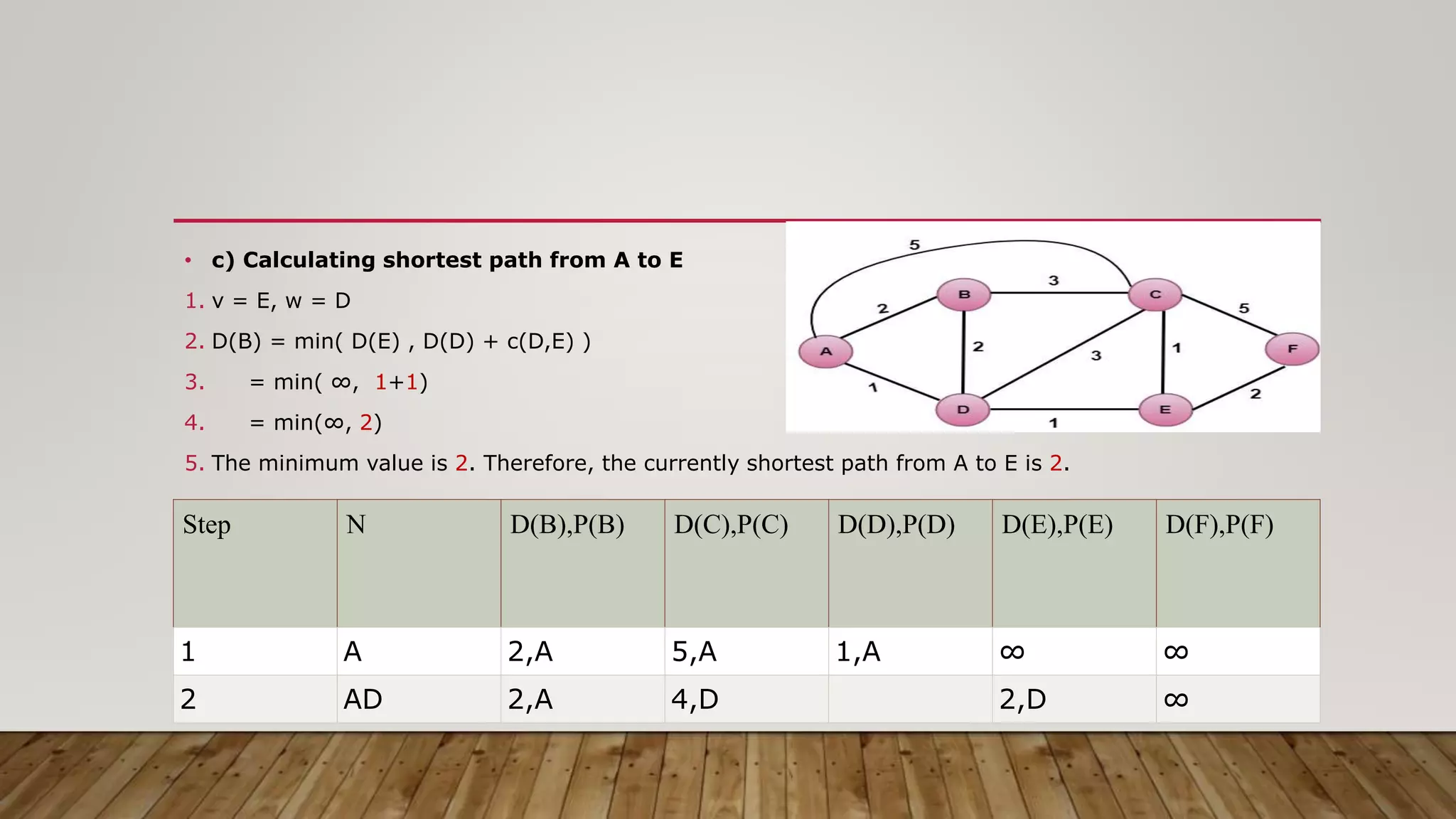
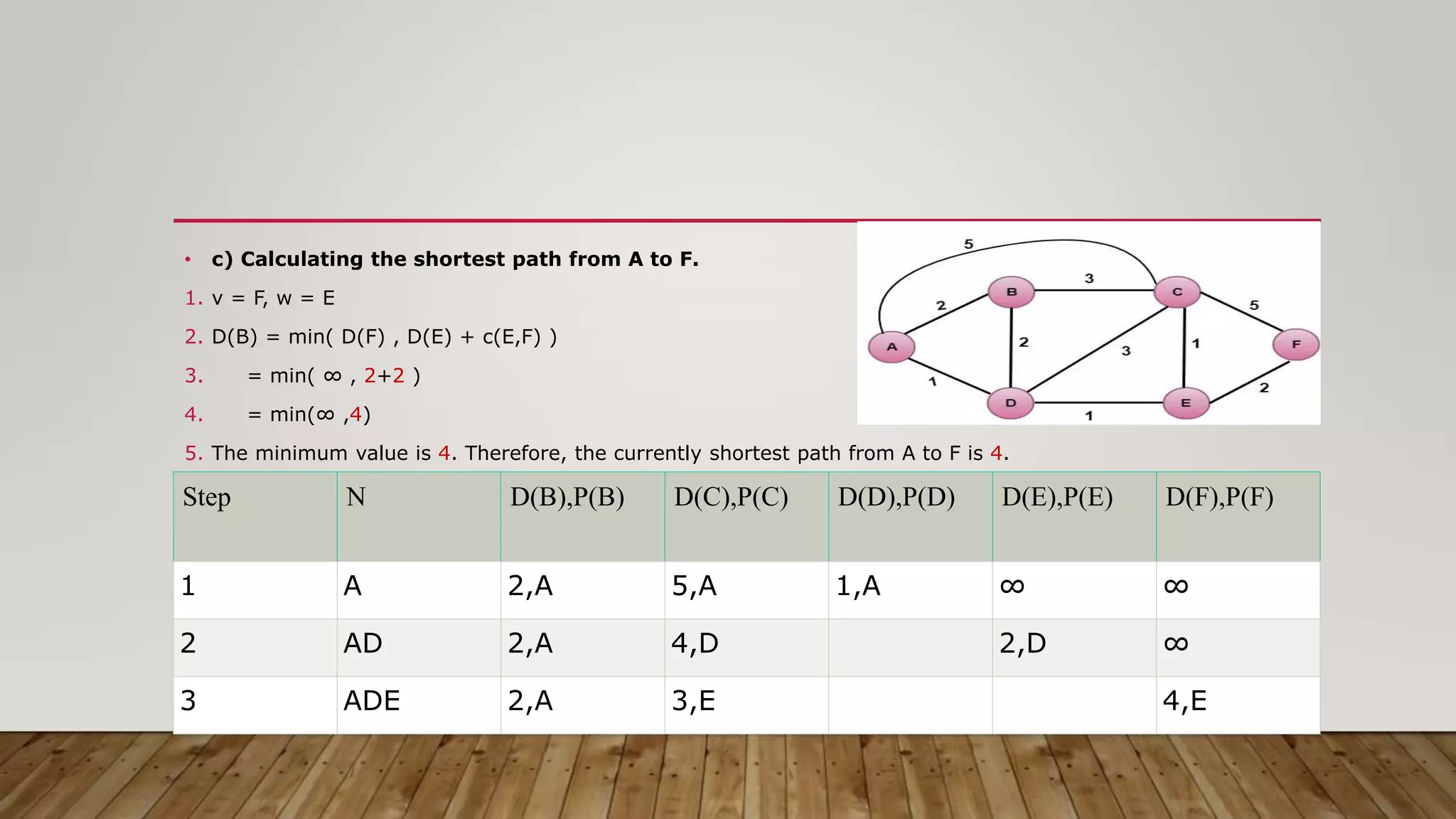
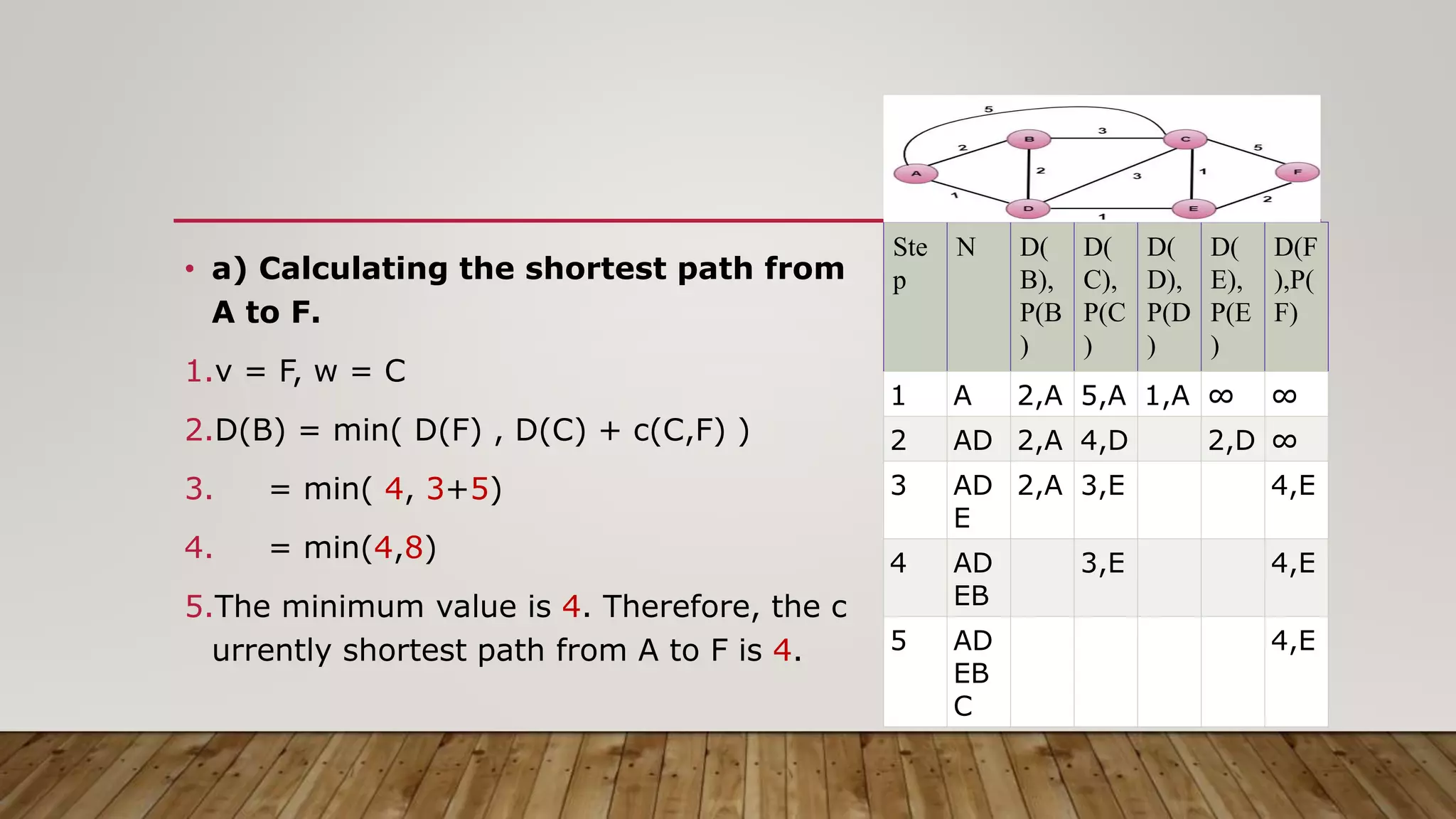
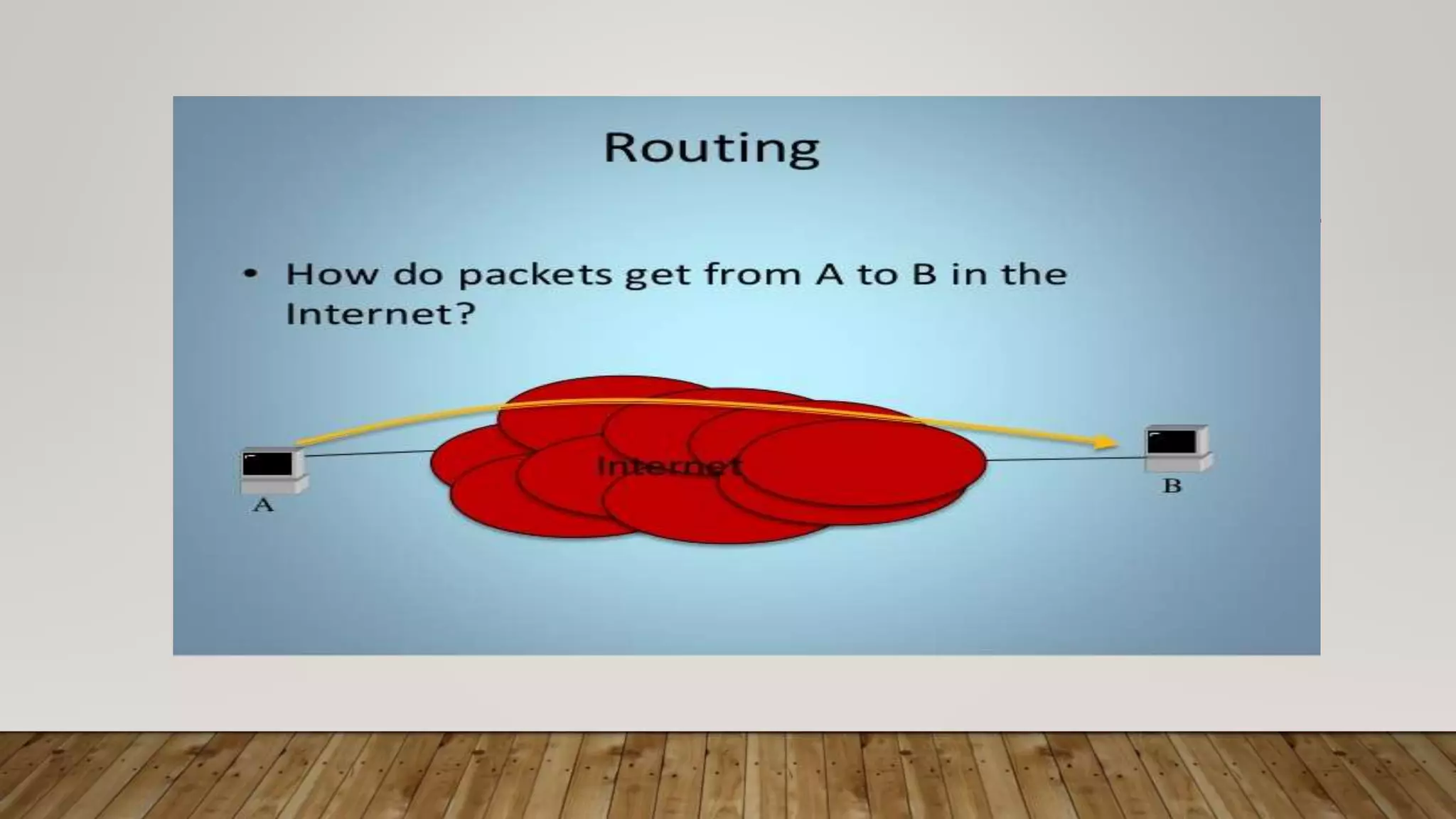
The document discusses routing algorithms in computer networks. It describes the key components of routers and their functions. It then explains the concepts of distance vector routing (DVR) and link state routing algorithms. For DVR, it provides an example to illustrate how routers calculate and update their routing tables using the Bellman-Ford algorithm. For link state routing, it explains the key steps of reliable flooding of link state information and route calculation using Dijkstra's algorithm through an example network topology. It compares the advantages and disadvantages of both routing approaches.









![Defines distance at each node:
dx(y)=cost of path x to y
[x=source,y=destination]
Update distance based on neighbours:
dx(y)=min{cost(x,v)+dv(y)}
[x=source,y=destination,v=intermediate node]](https://image.slidesharecdn.com/1703anusuabasu-201113172728/75/routing-algorithm-11-2048.jpg)