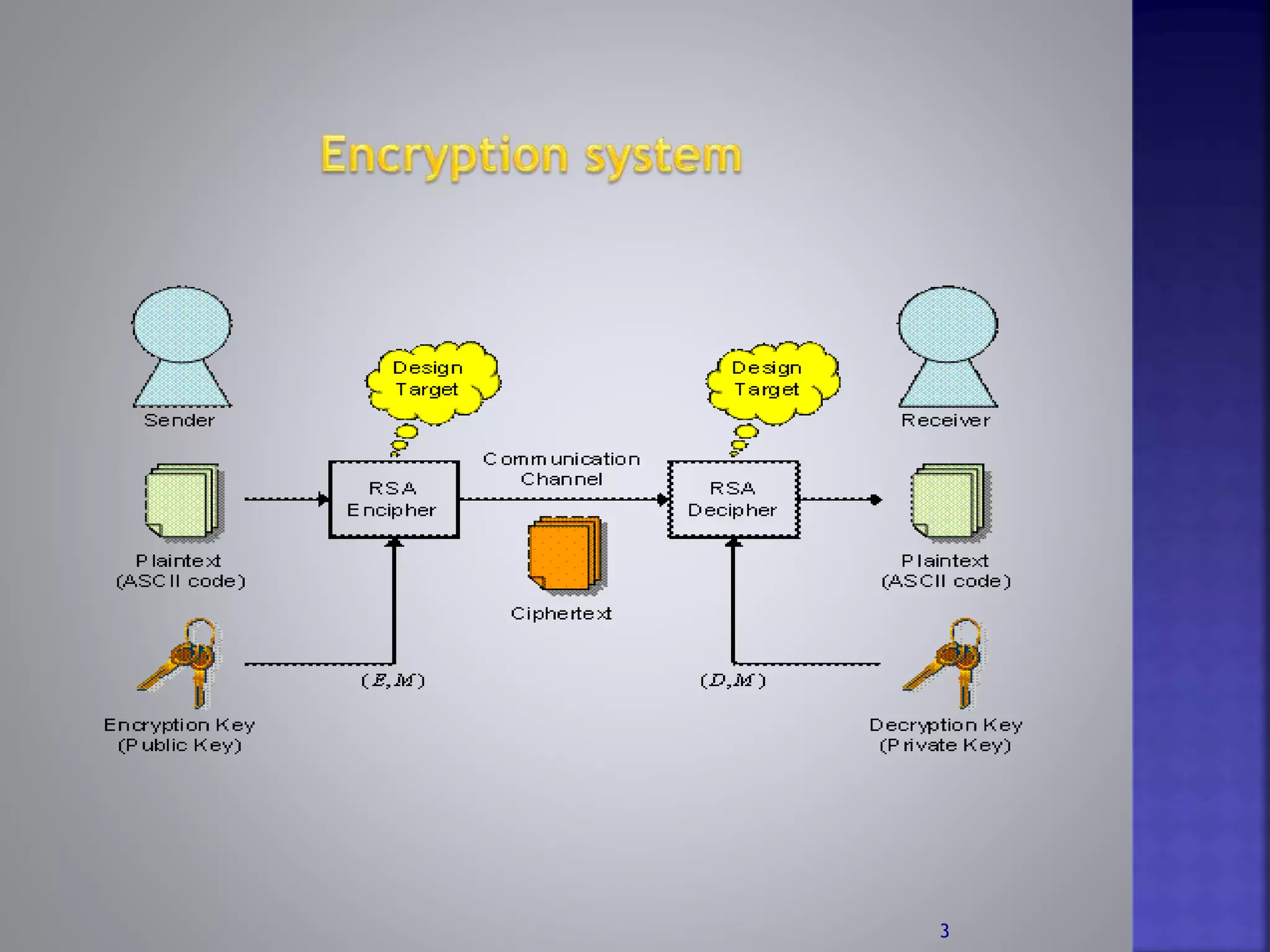
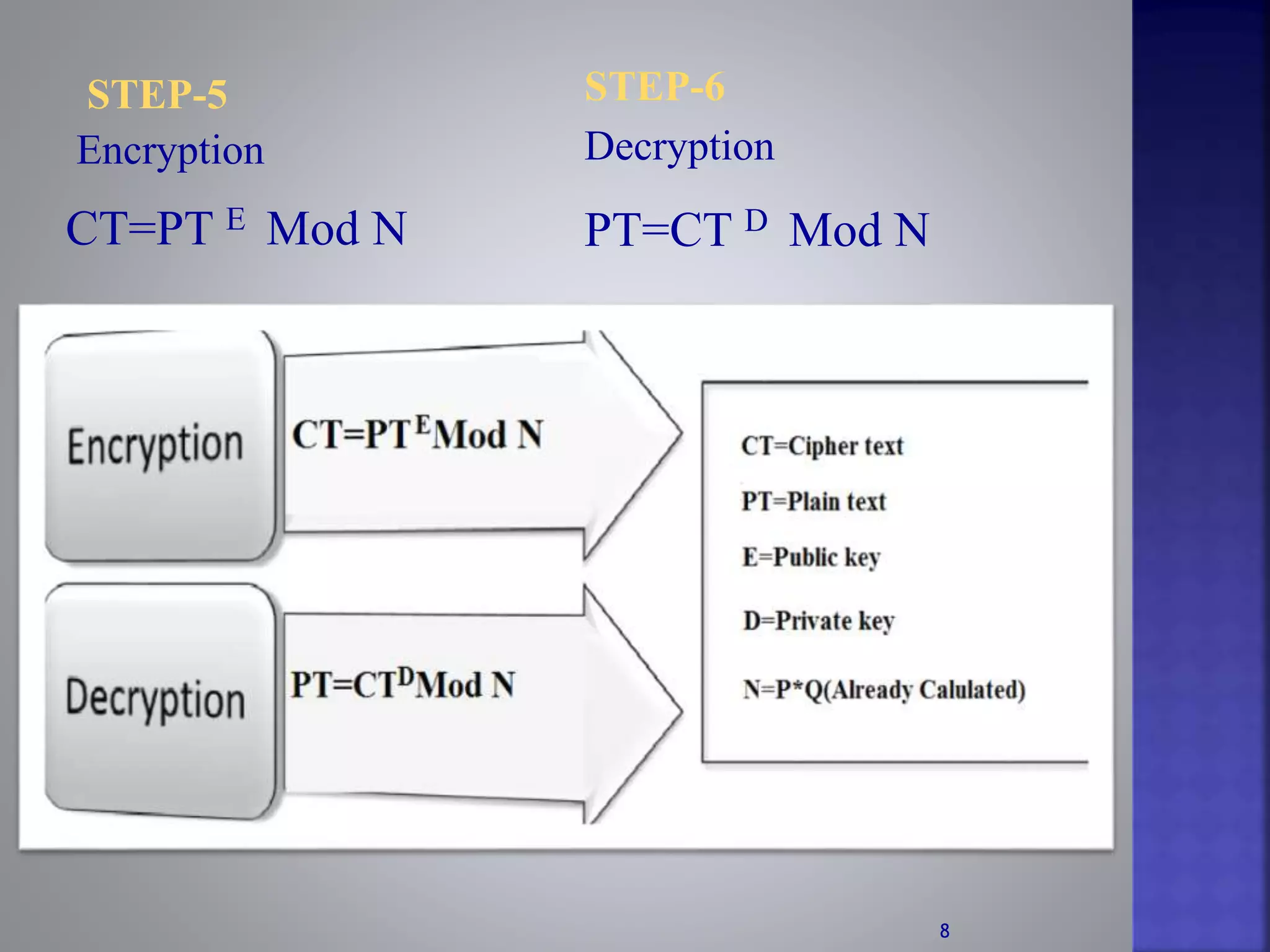
Rsa algorithm key generation

Rsa algorithm key generation

• 1.
  1
• 2.
  RSAAlgorithm is thefirst public key algorithm discovered by a group of three scientists namely Ron Rivest,Adi Shamir and Len Adleman and was first published in 1978. * RSAAlgorithm is based on the original work of Diffie. * It uses the key for encryption is different from (but related to ) the key used for decryption. * The RSA algorithm can be used for both public key encryption and digital signature purposes.*
• 3.
  3
• 4.
  * The Keysused for encryption and decryption in RSA algorithm, are generated using random data ( 300-400 digit). The key used for encryption is a public key and the key used for decryption is a private key. Public keys are stored anywhere publicly accessible. The sender of message encrypt the data using the receiver's public key, and the receiver decrypt it using its own private key. That’s why, no one else can intercept the data except receiver. * Continue.. 4
• 5.
  Select the twolargest random prime number P and Q to calculate the key. STEP -1 A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. Example:- 2,3,5,7,11,13,…………. etc 5
• 6.
  STEP -2 Calculate thesystem modulus –N of P and Q which is a common number for both public and private keys. N = P *Q STEP -3 Calculate Encryption key(E) as Find factors of (P-1)*(Q-1)  Choose E such that E should not divided by any factor of (P-1)*(Q-1) 6
• 7.
  STEP -4 Calculate decryptionkey (D) such that (E * D) mod (P-1)(Q-1) = 1 (P-1)(Q-1) * K + 1 = value1, value2,….. Where k = 1,2,3,…… 7
• 8.
  Encryption STEP-5 CT=PT E ModN STEP-6 Decryption PT=CT D Mod N 8
• 9.
  Consider RSA algorithmWhere P and Q are 17 and 11 respectively find E and D P=17 Q=11 Step-1 Calculate N N=P x Q N=17 x 11 N=187 9
• 10.
  Step-2 Calculate encryption key(E) Findfactorial of (P-1)(Q-1) =(17-1) (11-1) =(16) (10) =2 x 2 x 2 x 2 x 2 x 5 Now We choose E such that E should not divided by any factor of (P-1) x (Q-1) 10
• 11.
  Choose E=3 Step-3 => E xD mod (P-1)(Q-1)=1 => E x D mod 160 =1 => 3 x D mod 160 =1 160 x k + 1 , 160 x k + 1 161 , 321 => 3 x D = 321 => D=321/3 => D=107 Continue.. 11
• 12.
  12