Sorting algorithms bubble sort to merge sort.pdf

Sorting
• Sorting is a process that organizes a collection of data into either
ascending or descending order.
• An internal sort requires that the collection of data fit entirely in
the computer’s main memory.
• We can use an external sort when the collection of data cannot
fit in the computer’s main memory all at once but must reside in
secondary storage such as on a disk.
• We will analyze only internal sorting algorithms.
• A comparison-based sorting algorithm makes ordering decisions
only on the basis of comparisons.

Sorting Algorithms
• There are many sorting algorithms, such as:
– Selection Sort
– Insertion Sort
– Bubble Sort
– Merge Sort
– Quick Sort
• The first three are the foundations for faster
and more efficient algorithms.

Selection Sort
• The list is divided into two sublists, sorted and unsorted, which
are divided by an imaginary wall.
• We find the smallest element from the unsorted sublist and swap
it with the element at the beginning of the unsorted data.
• After each selection and swapping, the imaginary wall between
the two sublists move one element ahead, increasing the number
of sorted elements and decreasing the number of unsorted ones.
• Each time we move one element from the unsorted sublist to the
sorted sublist, we say that we have completed a sort pass.
• A list of n elements requires n-1 passes to completely rearrange
the data.

23 78 45 8 32 56
8 78 45 23 32 56
8 23 45 78 32 56
8 23 32 78 45 56
8 23 32 45 78 56
8 23 32 45 56 78
Original List
After pass 1
After pass 2
After pass 3
After pass 4
After pass 5
Sorted Unsorted

Selection Sort (cont.)
void selectionSort( int a[], int n) {
for (int i = 0; i < n-1; i++) {
int min = i;
for (int j = i+1; j < n; j++)
if (a[j] < a[min]) min = j;
int tmp = a[i];
a[i] = a[min];
a[min] = tmp;
}
}

Selection Sort -- Analysis
• In general, we compare keys and move items (or exchange items)
in a sorting algorithm (which uses key comparisons).
 So, to analyze a sorting algorithm we should count the
number of key comparisons and the number of moves.
• Ignoring other operations does not affect our final result.
• In selectionSort function, the outer for loop executes n-1 times.
• We invoke swap function once at each iteration.
 Total Swaps: n-1
 Total Moves: 3*(n-1) (Each swap has three moves)

Selection Sort – Analysis (cont.)
• The inner for loop executes the size of the unsorted part minus 1
(from 1 to n-1), and in each iteration we make one key
comparison.
 # of key comparisons = 1+2+...+n-1 = n*(n-1)/2
 So, Selection sort is O(n2)
• The best case, the worst case, and the average case of the
selection sort algorithm are same.  all of them are O(n2)
– This means that the behavior of the selection sort algorithm does not
depend on the initial organization of data.
– Since O(n2) grows so rapidly, the selection sort algorithm is appropriate
only for small n.

Insertion Sort
• Insertion sort is a simple sorting algorithm that is
appropriate for small inputs.
– Most common sorting technique used by card players.
• The list is divided into two parts: sorted and unsorted.
• In each pass, the first element of the unsorted part is
picked up, transferred to the sorted sublist, and inserted
at the appropriate place.
• A list of n elements will take at most n-1 passes to sort
the data.

Original List
After pass 1
After pass 2
After pass 3
After pass 4
After pass 5
23 78 45 8 32 56
23 78 45 8 32 56
23 45 78 8 32 56
8 23 45 78 32 56
8 23 32 45 78 56
8 23 32 45 56 78
Sorted Unsorted

Insertion Sort Algorithm
void insertionSort(int a[], int n)
{
for (int i = 1; i < n; i++)
{
int tmp = a[i];
for (int j=i; j>0 && tmp < a[j-1]; j--)
a[j] = a[j-1];
a[j] = tmp;
}
}

Insertion Sort – Analysis
• Running time depends on not only the size of the array but also
the contents of the array.
• Best-case:  O(n)
– Array is already sorted in ascending order.
– Inner loop will not be executed.
– The number of moves: 2*(n-1)  O(n)
– The number of key comparisons: (n-1)  O(n)
• Worst-case:  O(n2)
– Array is in reverse order:
– Inner loop is executed i-1 times, for i = 2,3, …, n
– The number of moves: 2*(n-1)+(1+2+...+n-1)= 2*(n-1)+ n*(n-1)/2  O(n2)
– The number of key comparisons: (1+2+...+n-1)= n*(n-1)/2  O(n2)
• Average-case:  O(n2)
– We have to look at all possible initial data organizations.
• So, Insertion Sort is O(n2)

Bubble Sort
• The list is divided into two sublists: sorted and
unsorted.
• The smallest element is bubbled from the unsorted
list and moved to the sorted sublist.
• After that, the wall moves one element ahead,
increasing the number of sorted elements and
decreasing the number of unsorted ones.
• Each time an element moves from the unsorted part to
the sorted part one sort pass is completed.
• Given a list of n elements, bubble sort requires up to
n-1 passes to sort the data.

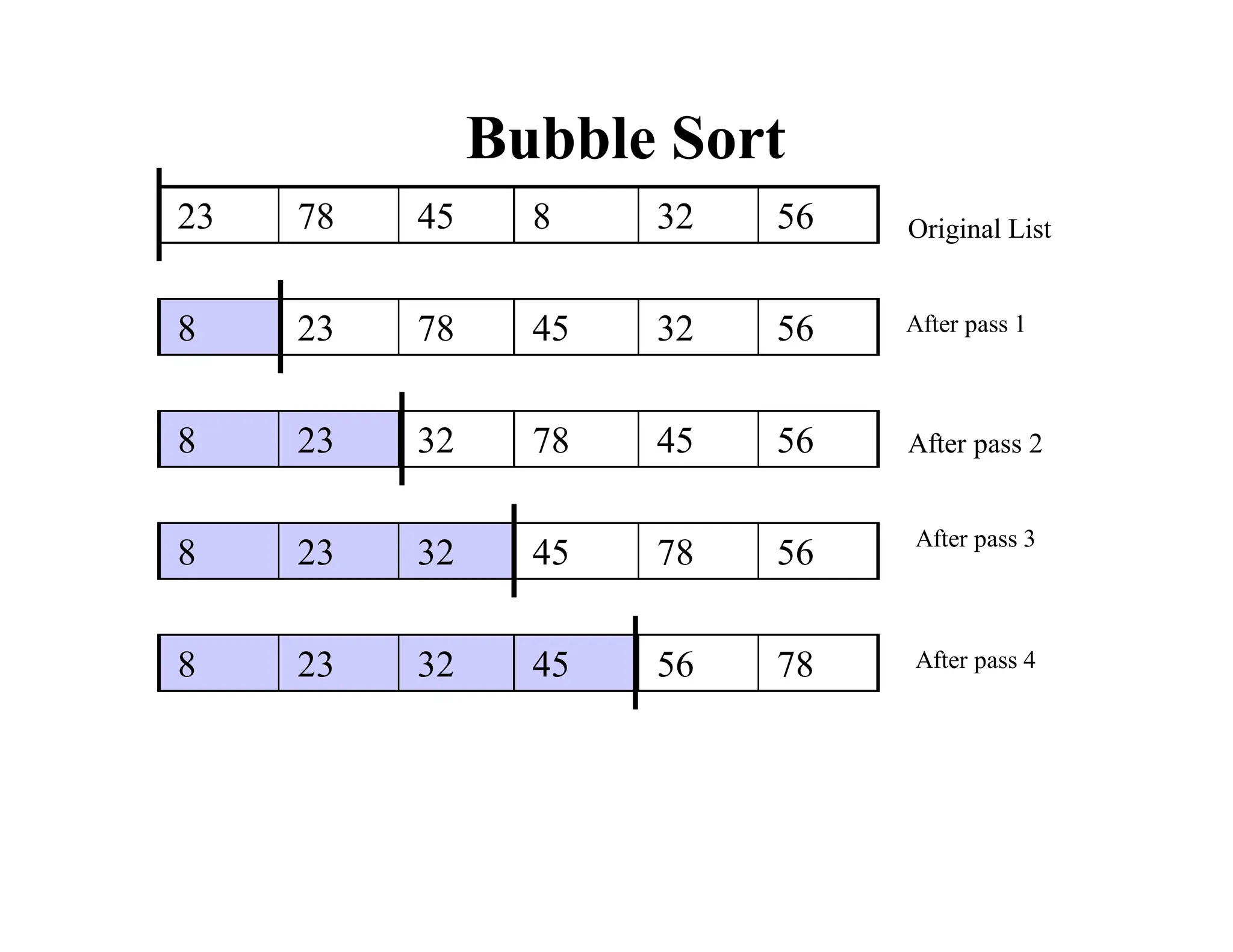
Bubble Sort
23 78 45 8 32 56
8 23 78 45 32 56
8 23 32 78 45 56
8 23 32 45 78 56
8 23 32 45 56 78
Original List
After pass 1
After pass 2
After pass 3
After pass 4

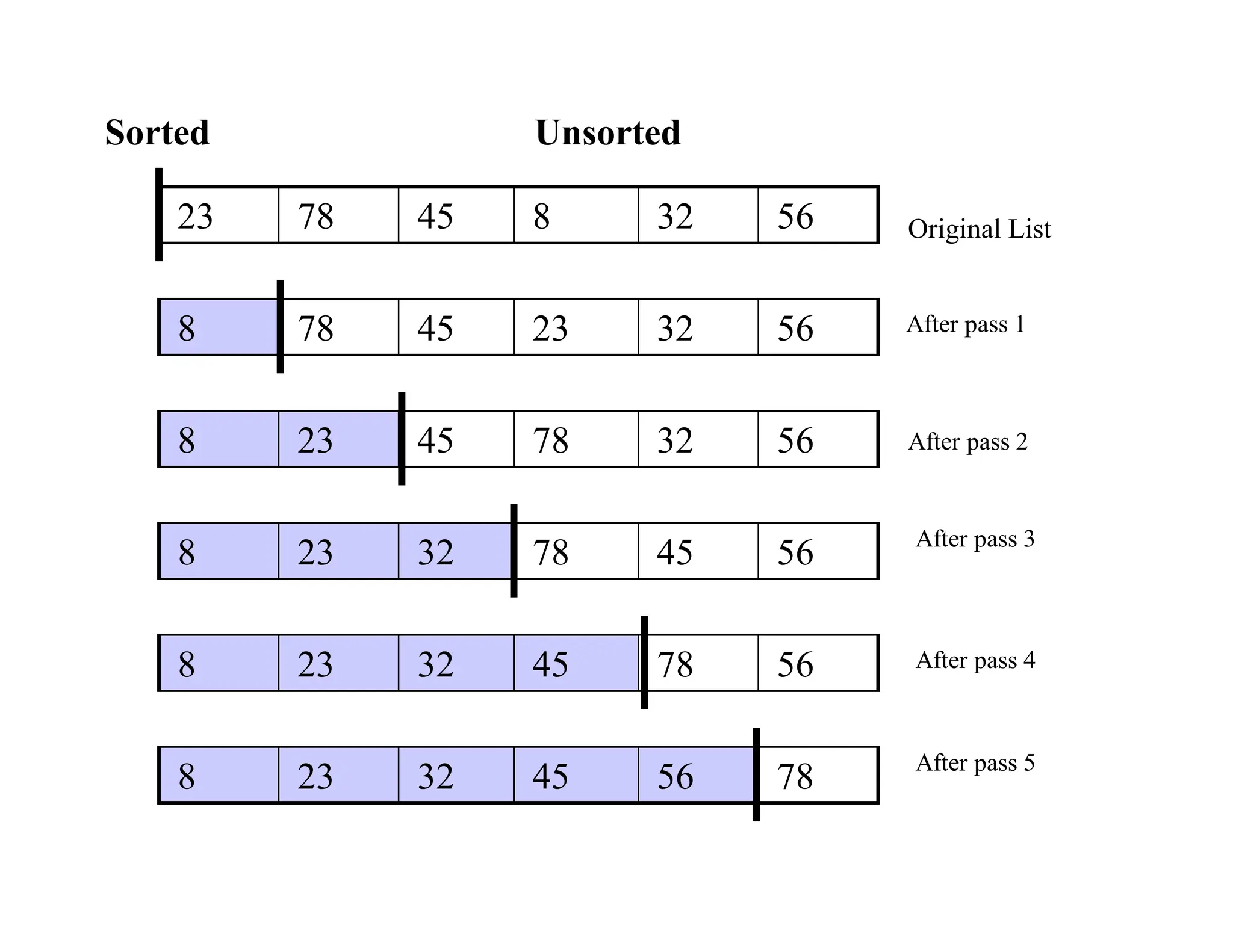
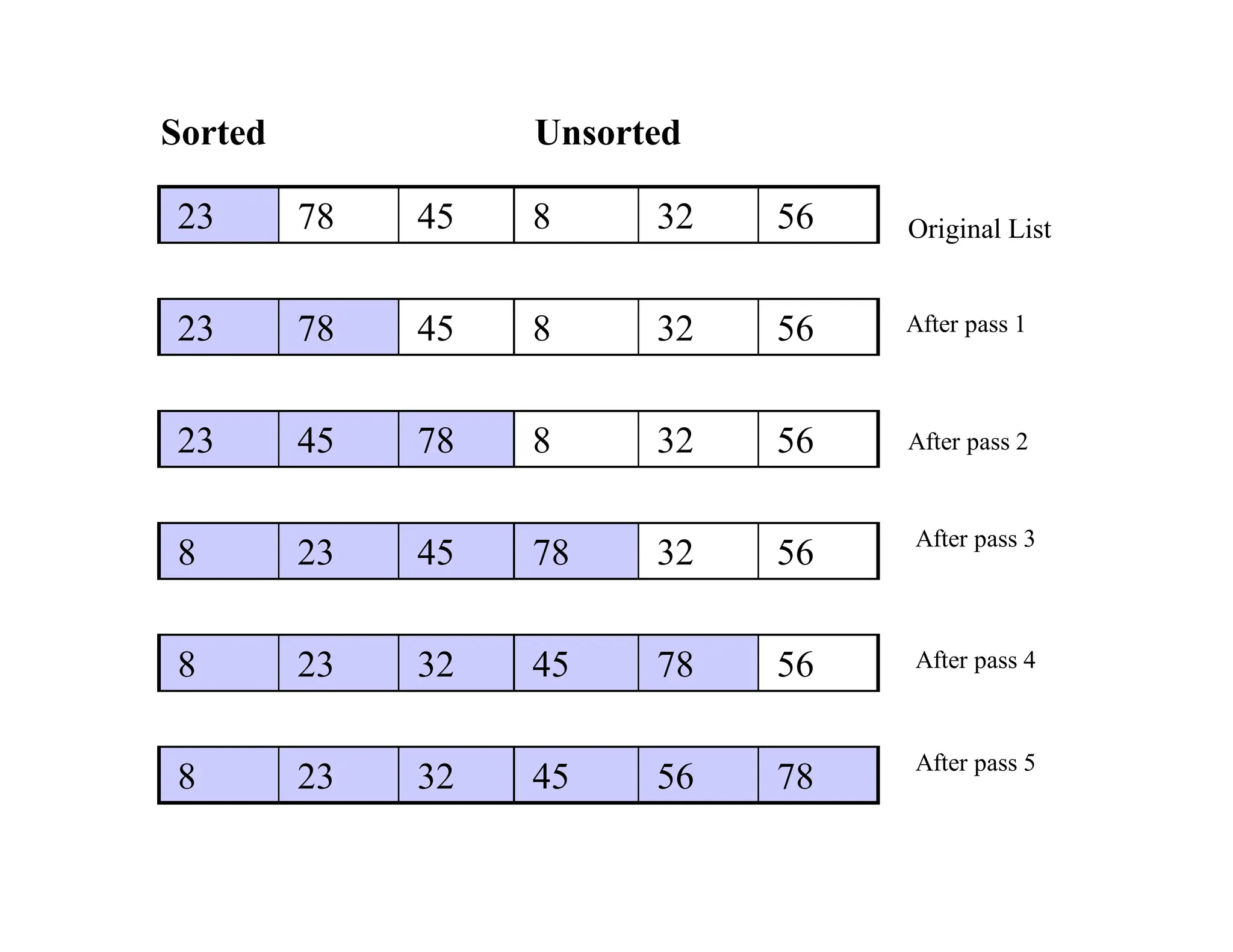
Bubble Sort Algorithm
void bubleSort(int a[], int n)
{
bool sorted = false;
int last = n-1;
for (int i = 0; (i < last) && !sorted; i++){
sorted = true;
for (int j=last; j > i; j--)
if (a[j-1] > a[j]{
int temp=a[j];
a[j]=a[j-1];
a[j-1]=temp;
sorted = false; // signal exchange
}
}
}

Bubble Sort – Analysis
• Best-case:  O(n)
– Array is already sorted in ascending order.
– The number of moves: 0  O(1)
– The number of key comparisons: (n-1)  O(n)
• Worst-case:  O(n2)
– Array is in reverse order:
– Outer loop is executed n-1 times,
– The number of moves: 3*(1+2+...+n-1) = 3 * n*(n-1)/2  O(n2)
– The number of key comparisons: (1+2+...+n-1)= n*(n-1)/2  O(n2)
• Average-case:  O(n2)
– We have to look at all possible initial data organizations.
• So, Bubble Sort is O(n2)

Mergesort
• Mergesort algorithm is one of two important divide-and-conquer
sorting algorithms (the other one is quicksort).
• It is a recursive algorithm.
– Divides the list into halves,
– Sort each halve separately, and
– Then merge the sorted halves into one sorted array.

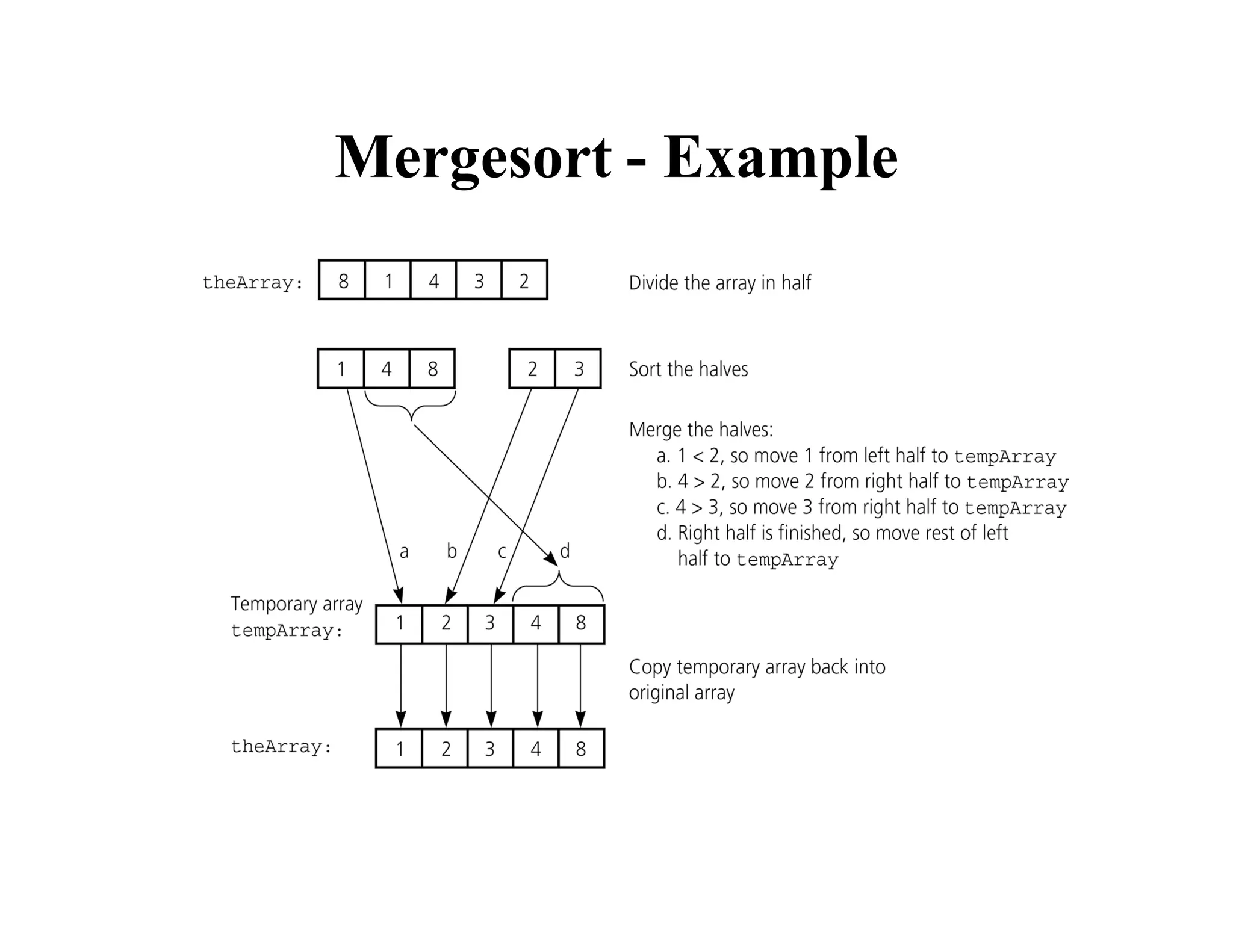
Merge
const int MAX_SIZE = maximum-number-of-items-in-array;
void merge(int theArray[], int first, int mid, int last) {
int tempArray[MAX_SIZE]; // temporary array
int first1 = first; // beginning of first subarray
int last1 = mid; // end of first subarray
int first2 = mid + 1; // beginning of second subarray
int last2 = last; // end of second subarray
int index = first1; // next available location in tempArray
for ( ; (first1 <= last1) && (first2 <= last2); ++index) {
if (theArray[first1] < theArray[first2]) {
tempArray[index] = theArray[first1];
++first1;
}
else {
++first2;
} }

Merge (cont.)
// finish off the first subarray, if necessary
for (; first1 <= last1; ++first1, ++index)
// finish off the second subarray, if necessary
for (; first2 <= last2; ++first2, ++index)
// copy the result back into the original array
for (index = first; index <= last; ++index)
theArray[index] = tempArray[index];
} // end merge

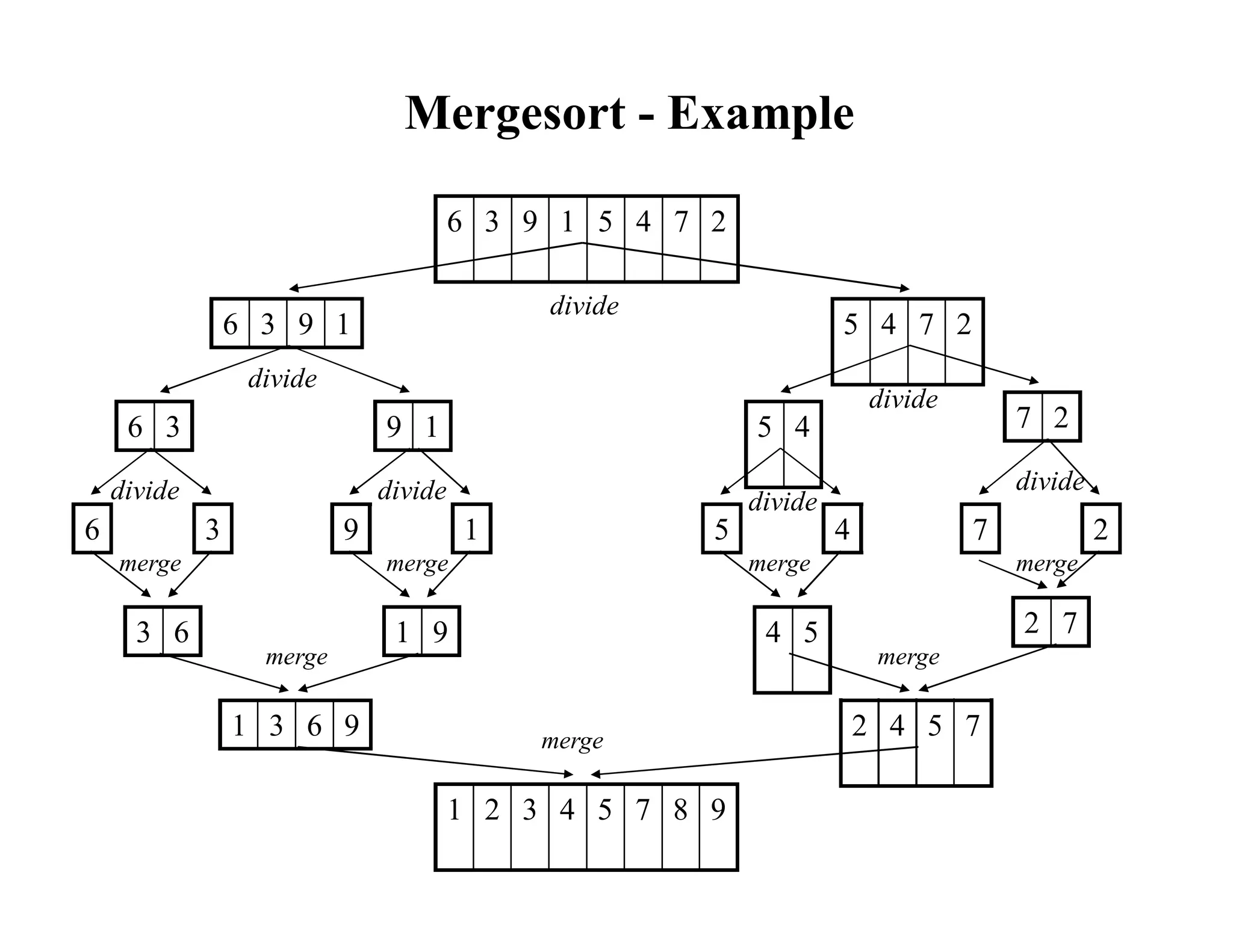
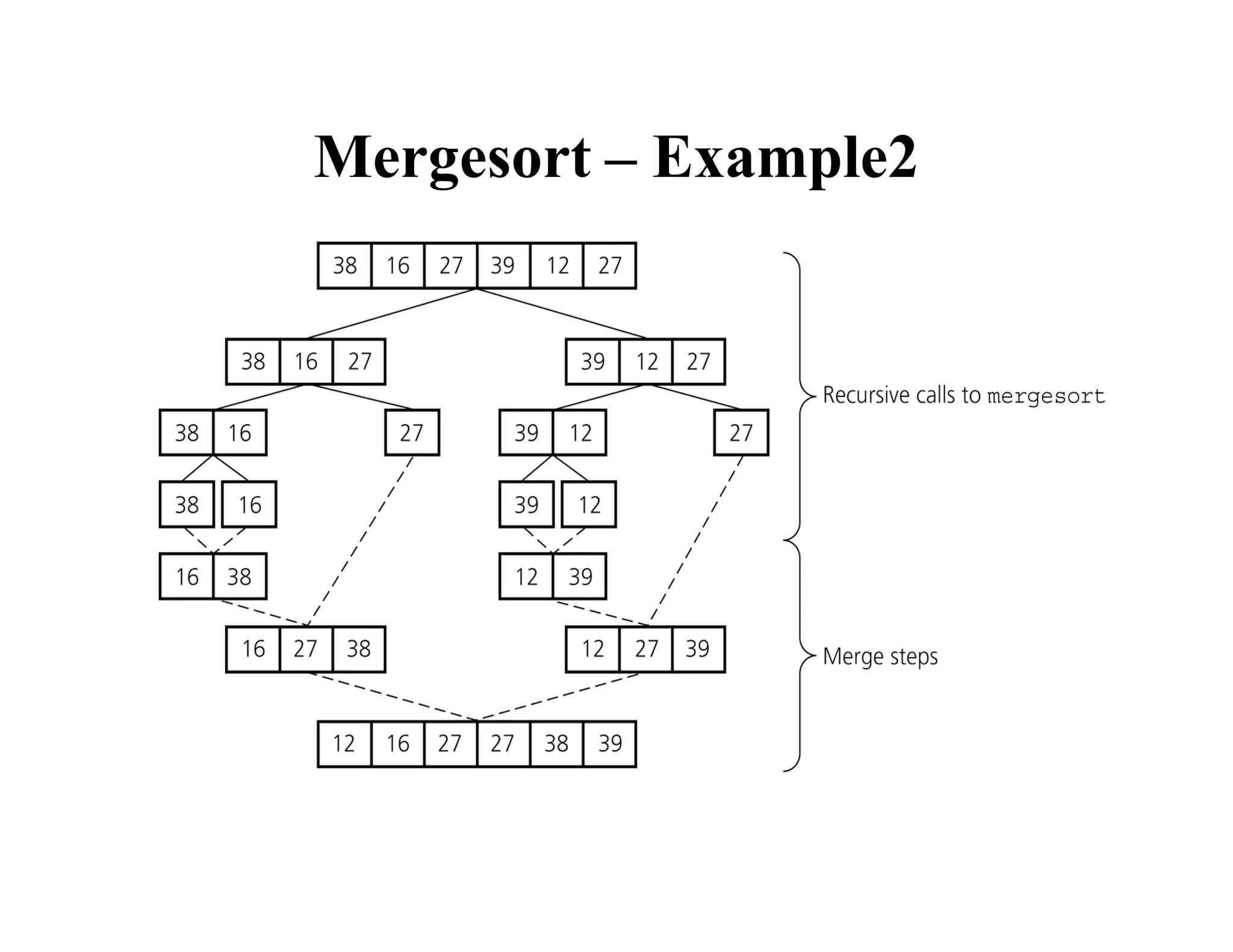
Mergesort
void mergesort(int theArray[], int first, int last) {
if (first < last) {
int mid = (first + last)/2; // index of midpoint
mergesort(theArray, first, mid);
mergesort(theArray, mid+1, last);
// merge the two halves
merge(theArray, first, mid, last);
}
} // end mergesort

Mergesort - Example
6 3 9 1 5 4 7 2
5 4 7 2
6 3 9 1
6 3 9 1 7 2
5 4
6 3 1
9 5 4 2
7
3 6 1 9 2 7
4 5
2 4 5 7
1 3 6 9
1 2 3 4 5 7 8 9
divide
divide
divide
divide
divide
divide
divide
merge merge
merge
merge
merge merge
merge

Mergesort – Analysis of Merge
A worst-case instance of the merge step in mergesort

Mergesort – Analysis of Merge (cont.)
Merging two sorted arrays of size k
• Best-case:
– All the elements in the first array are smaller (or larger) than all the
elements in the second array.
– The number of moves: 2k
– The number of key comparisons: k
• Worst-case:
– The number of moves: 2k
– The number of key comparisons: 2k-1
...... ......
......
0 k-1 0 k-1
0 2k-1

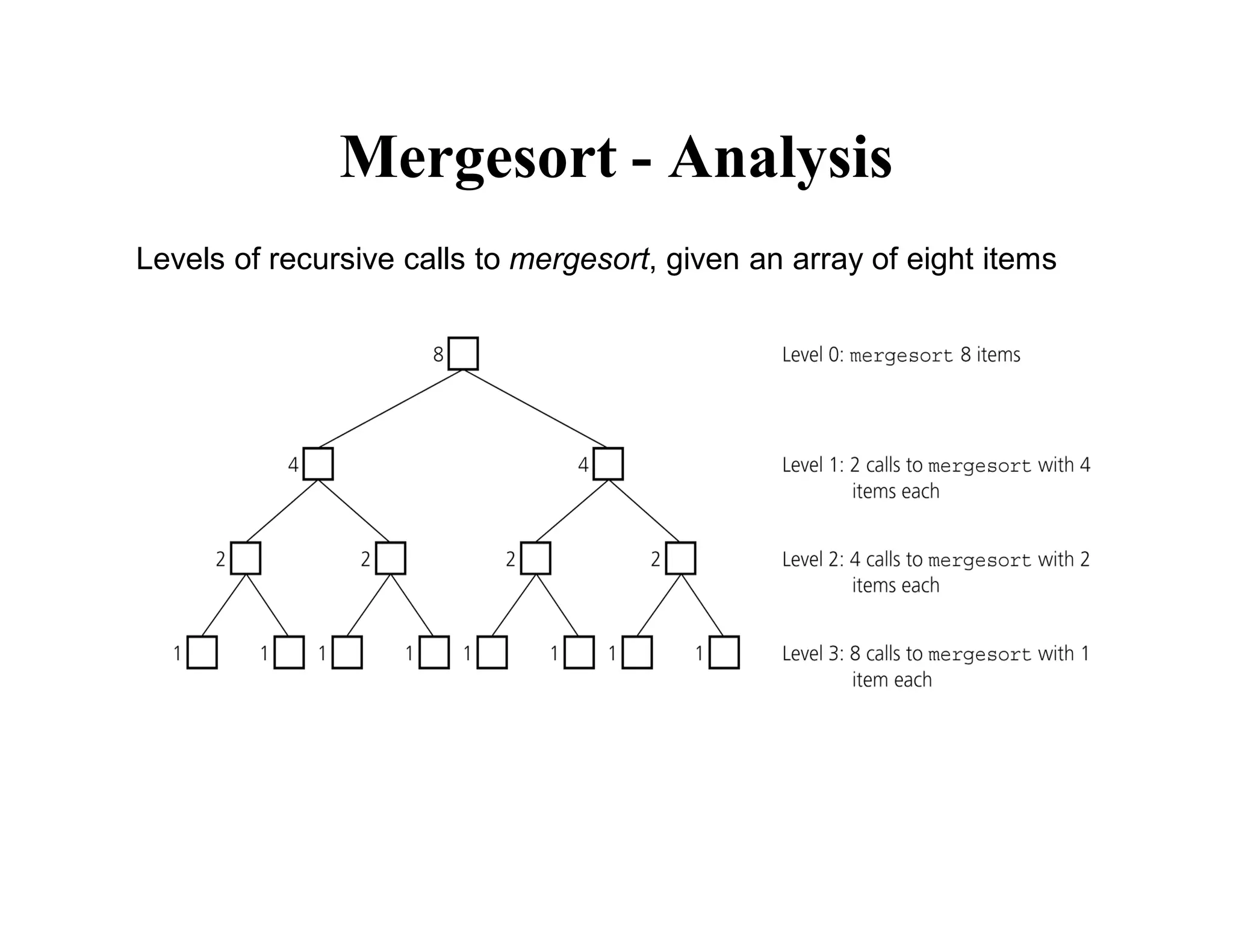
Mergesort - Analysis
Levels of recursive calls to mergesort, given an array of eight items

Mergesort – Recurrence Relation
T(n) = 2 T(n/2) + cn
= 2 [2 T(n/4) + cn/2] + cn
= 4 T(n/4) + 2cn
= 4 [2 T(n/8) + cn/4] + 2cn
= 8 T(n/8) + 3cn
…
…
= 2k T(n/2k) + kcn
We know that T(1) = 1
Putting n/2k = 1, we get n = 2k OR log2 n = k
Hence,
T(n)=nT(1)+cn log2n = n + cn log2n = O(log n)

Quicksort Algorithm
Given an array of n elements (e.g., integers):
• If array only contains one element, return
• Else
– pick one element to use as pivot.
– Partition elements into two sub-arrays:
• Elements less than or equal to pivot
• Elements greater than pivot
– Quicksort two sub-arrays
– Return results

Example
We are given array of n integers to sort:
40 20 10 80 60 50 7 30 100

Pick Pivot Element
There are a number of ways to pick the pivot element. In this
example, we will use the first element in the array:
40 20 10 80 60 50 7 30 100

Partitioning Array
Given a pivot, partition the elements of the array
such that the resulting array consists of:
1. One sub-array that contains elements >= pivot
2. Another sub-array that contains elements < pivot
The sub-arrays are stored in the original data array.
Partitioning loops through, swapping elements
below/above pivot.

40 20 10 80 60 50 7 30 100
pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
too_big_index too_small_index

40 20 10 80 60 50 7 30 100
pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
1. While data[too_big_index] <= data[pivot]
++too_big_index

40 20 10 80 60 50 7 30 100
pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
++too_big_index
2. While data[too_small_index] > data[pivot]
--too_small_index

40 20 10 80 60 50 7 30 100
pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
++too_big_index
--too_small_index
3. If too_big_index < too_small_index
swap data[too_big_index] and data[too_small_index]

40 20 10 30 60 50 7 80 100
pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
++too_big_index
--too_small_index

40 20 10 30 60 50 7 80 100
pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
++too_big_index
--too_small_index
4. While too_small_index > too_big_index, go to 1.

++too_big_index
--too_small_index
40 20 10 30 7 50 60 80 100
pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]

++too_big_index
--too_small_index
5. Swap data[too_small_index] and data[pivot_index]
40 20 10 30 7 50 60 80 100
pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]

++too_big_index
--too_small_index
7 20 10 30 40 50 60 80 100
pivot_index = 4
[0] [1] [2] [3] [4] [5] [6] [7] [8]

Partition Result
7 20 10 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
<= data[pivot] > data[pivot]

Recursion: Quicksort Sub-arrays
7 20 10 30 40 50 60 80 100
[0] [1] [2] [3] [4] [5] [6] [7] [8]
<= data[pivot] > data[pivot]

33
Complexity Analysis
T(N) = T(i) + T(N - i -1) + cN
The time to sort the file is equal to
 the time to sort the left partition
with i elements, plus
 the time to sort the right partition with
N-i-1 elements, plus
 the time to build the partitions.

34
Worst-Case Analysis
The pivot is the smallest (or the largest) element
T(N) = T(N-1) + cN, N > 1
Telescoping:
T(N-1) = T(N-2) + c(N-1)
T(N-2) = T(N-3) + c(N-2)
T(N-3) = T(N-4) + c(N-3)
…………...
T(2) = T(1) + c.2

35
Worst-Case Analysis
T(N) + T(N-1) + T(N-2) + … + T(2) =
= T(N-1) + T(N-2) + … + T(2) + T(1) +
c(N) + c(N-1) + c(N-2) + … + c.2
T(N) = T(1) +
c times (the sum of 2 thru N)
= T(1) + c (N (N+1) / 2 -1) = O(N2)

36
Best-Case Analysis
The pivot is in the middle
T(N) = 2T(N/2) + cN
Like mergesort
T(N)=O(N log N)

Quicksort: Worst Case
• Assume first element is chosen as pivot.
• Assume we get array that is already in
order:
2 4 10 12 13 50 57 63 100
pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]

++too_big_index
--too_small_index
2 4 10 12 13 50 57 63 100
pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]

++too_big_index
--too_small_index
2 4 10 12 13 50 57 63 100
pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
> data[pivot]
<= data[pivot]

Improved Pivot Selection
Pick median value of three elements from data array:
data[0], data[n/2], and data[n-1].
Use this median value as pivot.
However selection of median value takes O(n) time.

Radix Sort
Sort by keys
K0, K1, …, Kr-1
Most significant key Least significant key
R0, R1, …, Rn-1 are said to be sorted w.r.t. K0, K1, …, Kr-1 iff
( , ,..., ) ( , ,..., )
k k k k k k
i i i
r
i i i
r
0 1 1
1
0
1
1
1
1

  

 0i<n-1
Most significant digit first: sort on K0, then K1, ...
Least significant digit first: sort on Kr-1, then Kr-2, ...

Radix Sort
0  K  999
(K0, K1, K2)
MSD LSD
0-9 0-9 0-9
radix 10 sort
radix 2 sort

Example for LSD Radix Sort
front[0] NULL rear[0]
front[1] 271 NULL rear[1]
front[3] 93 33 NULL rear[3]
front[9] 179 859 9 NULL rear[9]
179, 208, 306, 93, 859, 984, 55, 9, 271, 33
271, 93, 33, 984, 55, 306, 208, 179, 859, 9 After the first pass
Sort
by
digit
concatenate
d (digit) = 3, r (radix) = 10 ascending order

306 208 9 null
null
null
33 null
null
55 859 null
null
271 179 null
984 null
93 null
rear[0]
rear[1]
rear[2]
rear[3]
rear[4]
rear[5]
rear[6]
rear[7]
rear[8]
rear[9]
front[0]
front[1]
front[2]
front[3]
front[4]
front[5]
front[6]
front[7]
front[8]
front[9]
306, 208, 9, 33, 55, 859, 271, 179, 984, 93 (second pass)

9 33 55
306 null
null
null
859 null
984 null
rear[0]
rear[1]
rear[2]
rear[3]
rear[4]
rear[5]
rear[6]
rear[7]
rear[8]
rear[9]
front[0]
front[1]
front[2]
front[3]
front[4]
front[5]
front[6]
front[7]
front[8]
front[9]
9, 33, 55, 93, 179, 208, 271, 306, 859, 984 (third pass)
93 null
179 null
208 271 null
null
null

Time Complexity of Radix Sort
If d is the maximum number of digits in any key
and there are n keys then the worst case time
complexity of Radix sort is O(dn).

Stable sort algorithms
• A stable sort keeps
equal elements in the
same order
• This may matter when
you are sorting data
according to some
characteristic
• Example: sorting
students by test scores
Bob
Ann
Joe
Zöe
Dan
Pat
Sa
m
90
98
98
86
75
86
90
original
array
Bob
Ann
Joe
Zöe
Dan
Pat
Sa
m
90
98
98
86
75
86
90
stably
sorted

Unstable sort algorithms
• An unstable sort
may or may not
keep equal
elements in the
same order
• Stability is usually
not important, but
sometimes it is
important
Bob
Ann
Joe
Zöe
Dan
Pat
Sa
m
90
98
98
86
75
86
90
original
array
Bob
Ann
Joe
Zöe
Dan
Pat
Sa
m
90
98
98
86
75
86
90
unstably
sorted

Sorting algorithms bubble sort to merge sort.pdf

More Related Content

Similar to Sorting algorithms bubble sort to merge sort.pdf

Recently uploaded

Sorting algorithms bubble sort to merge sort.pdf