Unit 7 sorting

Sorting
Kalyani Neve
Asst.Prof.
GHRIBM,Jalgaon

In computer science, a sorting algorithm is an algorithm that
puts elements of a list in a certain order. Ordering the data in an
increasing or decreasing fashion according to some relationship
among the data item is called sorting.
Efficient sorting is important for optimizing the use of other
algorithms (such as search and merge algorithms) that require sorted
lists to work correctly.
Two main classification of sorting :
1. Internal Sorting Internal sorting is a process of sorting the data
in the main memory.
2. External Sorting External sorting is process of sorting in which
large blocks of data stored in storage devices
are moved to the main memory and then
sorted.

1.Insertion Sort :
Suppose an array A with n elements A[1], A[2],…..,A[n] is in
memory. The insertion sort algorithm. Scans A from A[1] to A[n],
inserting each element A[K] into its proper position in the
previously sorted sub array A[1], A[2], …,A[K-1]. That is:
Pass 1: A[1] by itself is trivially sorted.
Pass 2: A[2] is inserted either before or after A[1] so that A[1], A[2]
is sorted.
Pass 3: A[3] is inserted into its proper place in A[1], A[2], that is
before A[1], between A[1] and A[2], or after A[2], So that
A[1], A[2],A[3] is sorted.

Pass 4: A[4] is inserted into its proper place in A[1],A[2],A[3]
so that:
A[1],A[2],A[3],A[4] is sorted.
.
.
.
.
.
Pass N : A[N] is inserted into its proper place in
A[1],A[2],…,A[N-1] so that :
A[1],A[2],……,A[N] is sorted.

Algorithm :
INSERTION(A,N)
1. Set A[0] := -∞ [Initializes element]
2. Repeat Steps 3 to 5 for K = 2,3,…..,N:
3. Set TEMP := A[K] and PTR := K-1
4. Repeat while TEMP < A[PTR]:
1. Set A[PTR + 1] := A[PTR]. [Moves element
forward.]
2. Set PTR := PTR – 1
5. Set A[PTR + 1] := TEMP [Inserts element in proper
place.]
[End of Step 2 loop.]
6. Return

Pass A[0] A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8]
K=1: -∞ 33 44 11 88 22 66 55
K=2: -∞ 77 33 44 11 88 22 66 55
K=3: -∞ 33 77 44 11 88 22 66 55
K=4: -∞ 33 44 77 11 88 22 66 55
K=5: -∞ 11 33 44 77 88 22 66 55
K=6: -∞ 11 33 44 77 88 22 66 55
K=7: -∞ 11 22 33 44 77 88 66 55
K=8: -∞ 11 22 33 44 66 77 88 55
Sorted: -∞ 11 22 33 44 55 66 77 88
Array A is, 77, 33, 44, 11, 88, 22, 66, 55
77

2. Selection Sort :
memory. The selection sort algo. For sorting A as follows:
Pass 1: Find the location LOC of the smallest in the list of N elements
A[1],A[2],….,A[N], and then interchange A[LOC] and A[1],
Then : A[1] is sorted.
Pass 2: Find the location LOC of the smallest in the sublist of N-1
elements A[1],A[2],….,A[N], and then interchange A[LOC]
and A[2], Then : A[1], A[2]is sorted. Since A[1] <= A[2].
Pass 3:Find the location LOC of the smallest in the sub list of N-2
elements A[1],A[2],….,A[N], and then interchange A[LOC]
and A[3], Then : A[1], A[2],A[3]is sorted. Since A[2] <= A[3].

.
.
.
Pass N-1:Find the location LOC of the smaller of the elements
A[N-1],A[N], and then interchange A[LOC] and A[N-
1], Then : A[1],A[2],….A[N]is sorted.
Since A[N-1] <= A[N].
Thus A is sorted after N-1 passes.

Algorithm :
SELECTION(A,N)
1. Repeat Steps 2 and 3 for K=1,2,….,N-1
2. Call Min (A,K,N,LOC)
3. [Interchange A[K] and A[LOC]]
Set TEMP := A[K], A[K] := A{LOC] and A[LOC] :=
TEMP
[End of step 1 loop]
4. Exit
MIN(A,K,N,LOC)
1. Set MIN := A[K] and LOC := K. [Initialize pointers]
2. Repeat for J=K+1,K+2,….,N
If MIN > A[J], then :
Set MIN := A[J] and LOC := A[J] and LOC := J
[End of loop]
3. Return

Pass A[1] A[2] A[3] A[4] A[5] A[6] A[7] A[8]
K=1:
LOC=4
33 44 11 88 22 66 55
K=2:
LOC=6
11 33 44 77 88 22 66 55
K=3:
LOC=6
11 22 44 77 88 33 66 55
K=4:
LOC=6
11 22 33 77 88 44 66 55
K=5:
LOC=8
11 22 33 44 88 77 66 55
K=6:
LOC=7
11 22 33 44 55 77 66 88
K=7:
LOC=7
11 22 33 44 55 66 77 88
Sorted: 11 22 33 44 55 66 77 88
Array A is, 77, 33, 44, 11, 88, 22, 66, 55
77

3. Bubble Sort :
memory. The bubble sort algo. For sorting A as follows:
Step 1: Compare A[1] and A[2] and arrange them in the desired
order, so that A[1] < A[2]. Then compare A[2] and A[3] and
arrange them so that A[2] < A[3]. Continue until we compare
A[N-1] with A[N] and arrange them.
Step 2: Repeat step 1 with one less comparison, that is, now we
stop after we compare and possibly rearrange A[N-1] and A[N-
1].
.
.
.

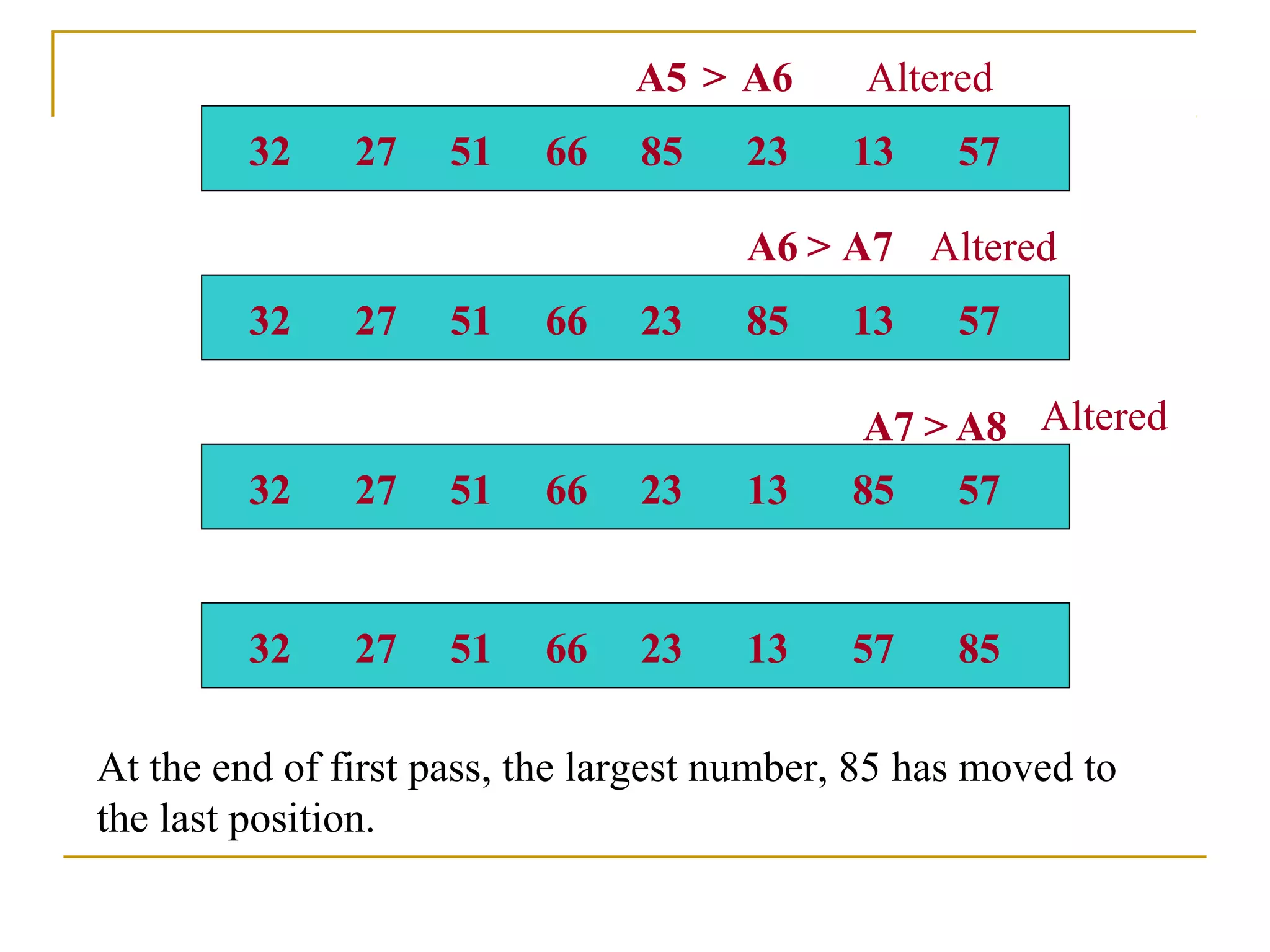
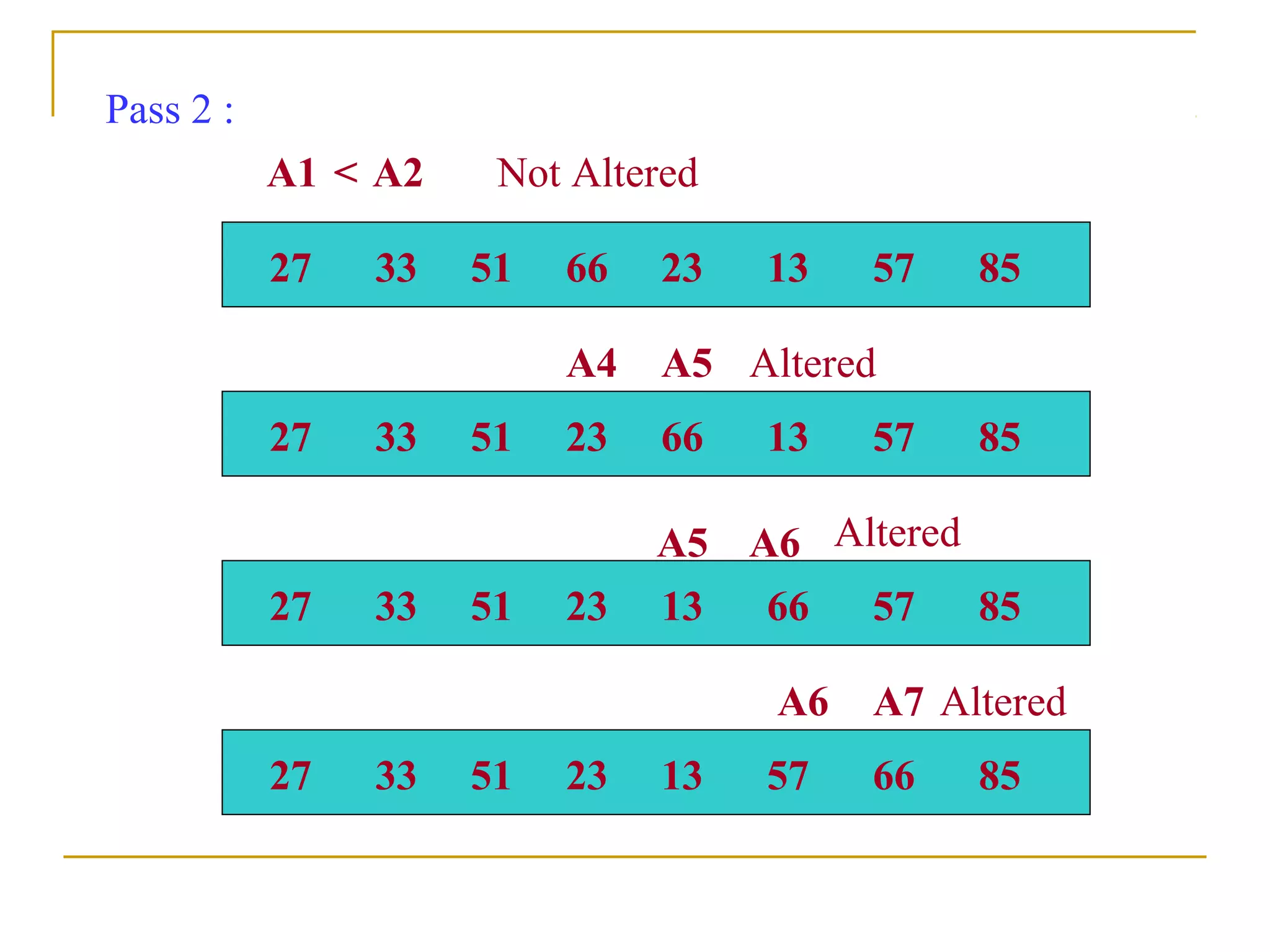
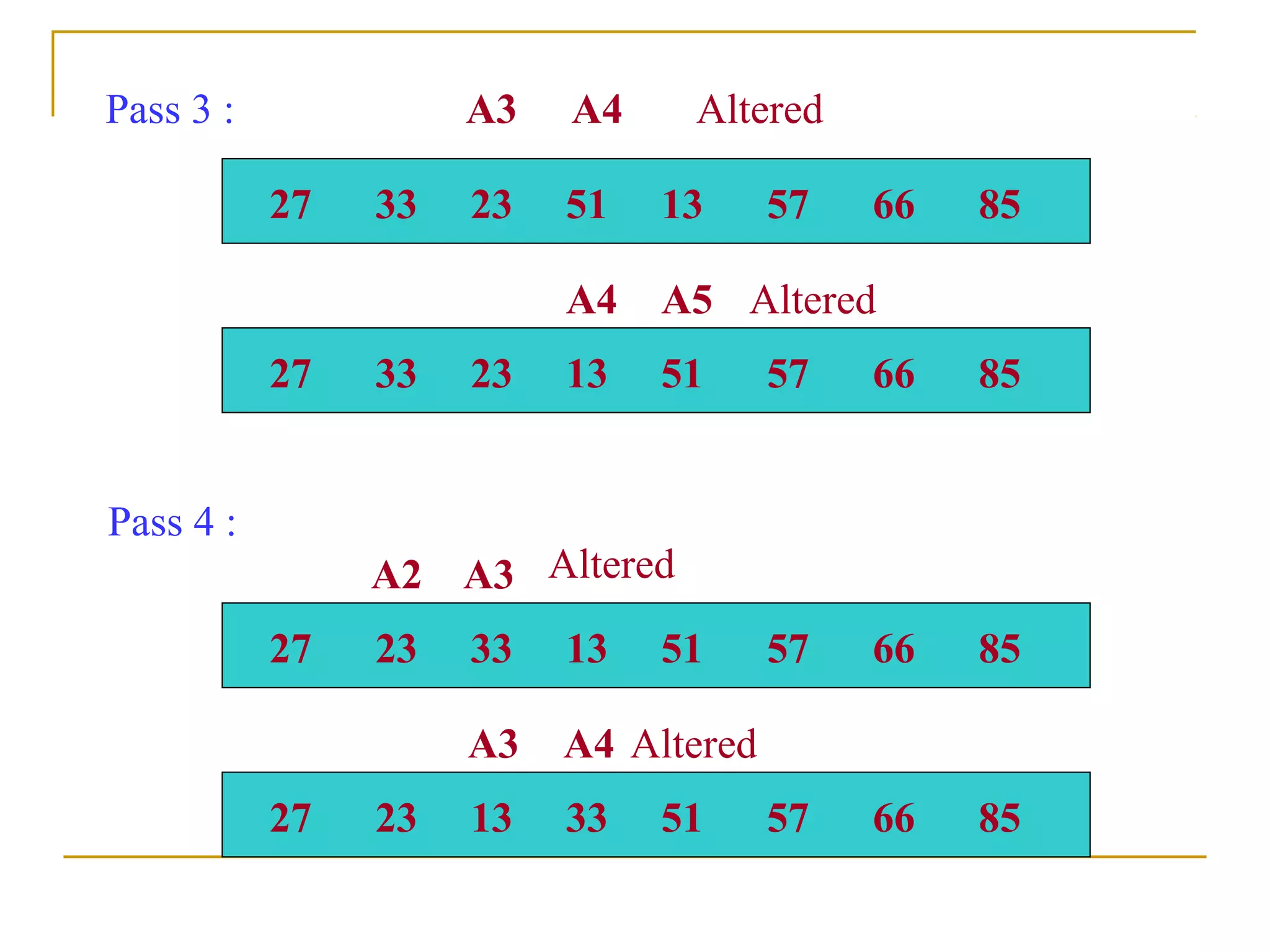
Step N-1 : Compare A[1] with A[2] and arrange them so that
A[1] < A[2].
After N-1 steps, the list will be sorted in increasing order.
Suppose the following numbers are sorted in an array A :
32, 51, 27,85, 66, 23, 13, 57
We apply the bubble sort to the array A.

BUBBLE(DATA, N)
Here DATA is an array with N elements. This algorithm sorts the
elements in DATA.
1. Repeat steps 2 and 3 for K = 1 to N-1.
2. Set PTR := 1. [ Initialize pass pointer PTR]
3. Repeat while PTR <= N – K: [Execute pass]
1. If DATA[PTR] > DATA[PTR + 1], then :
Interchange DATA[PTR] and DATA[PTR + 1]
[End of If structure]
2. Set PTR := PTR + 1.
[End of inner loop]
[End of step 1 outer loop]
4. Exit

Pass 1: We have the following comparisons :
32 51 27 85 66 23 13 57
32 51 27 85 66 23 13 57
32 27 51 85 66 23 13 57
32 27 51 85 66 23 13 57
A1 A2<
>A2 A3
<A3 A4
A4 A5>
Not Altered
Altered
Not Altered
Altered

32 27 51 66 85 23 13 57
32 27 51 66 23 85 13 57
32 27 51 66 23 13 85 57
32 27 51 66 23 13 57 85
A5 A6>
>A6 A7
>A7 A8
Altered
Altered
Altered
At the end of first pass, the largest number, 85 has moved to
the last position.

Pass 2 :
27 33 51 66 23 13 57 85
27 33 51 23 66 13 57 85
27 33 51 23 13 66 57 85
27 33 51 23 13 57 66 85
A1 A2<
A4 A5
A5 A6
A6 A7
Not Altered
Altered
Altered
Altered

Pass 3 :
27 33 23 51 13 57 66 85
27 33 23 13 51 57 66 85
27 23 33 13 51 57 66 85
27 23 13 33 51 57 66 85
A3 A4
A4 A5
A2 A3
A3 A4
Altered
Altered
Altered
Altered
Pass 4 :

23 27 13 33 51 57 66 85
23 13 27 33 51 57 66 85
A1 A2
A2 A3
Altered
Altered
Pass 5 :
13 23 27 33 51 57 66 85
A1 A2 Altered
Pass 6 :
Pass 7 : Finally, A1 is compared with A2. No interchange takes
place. Since the list is sorted.

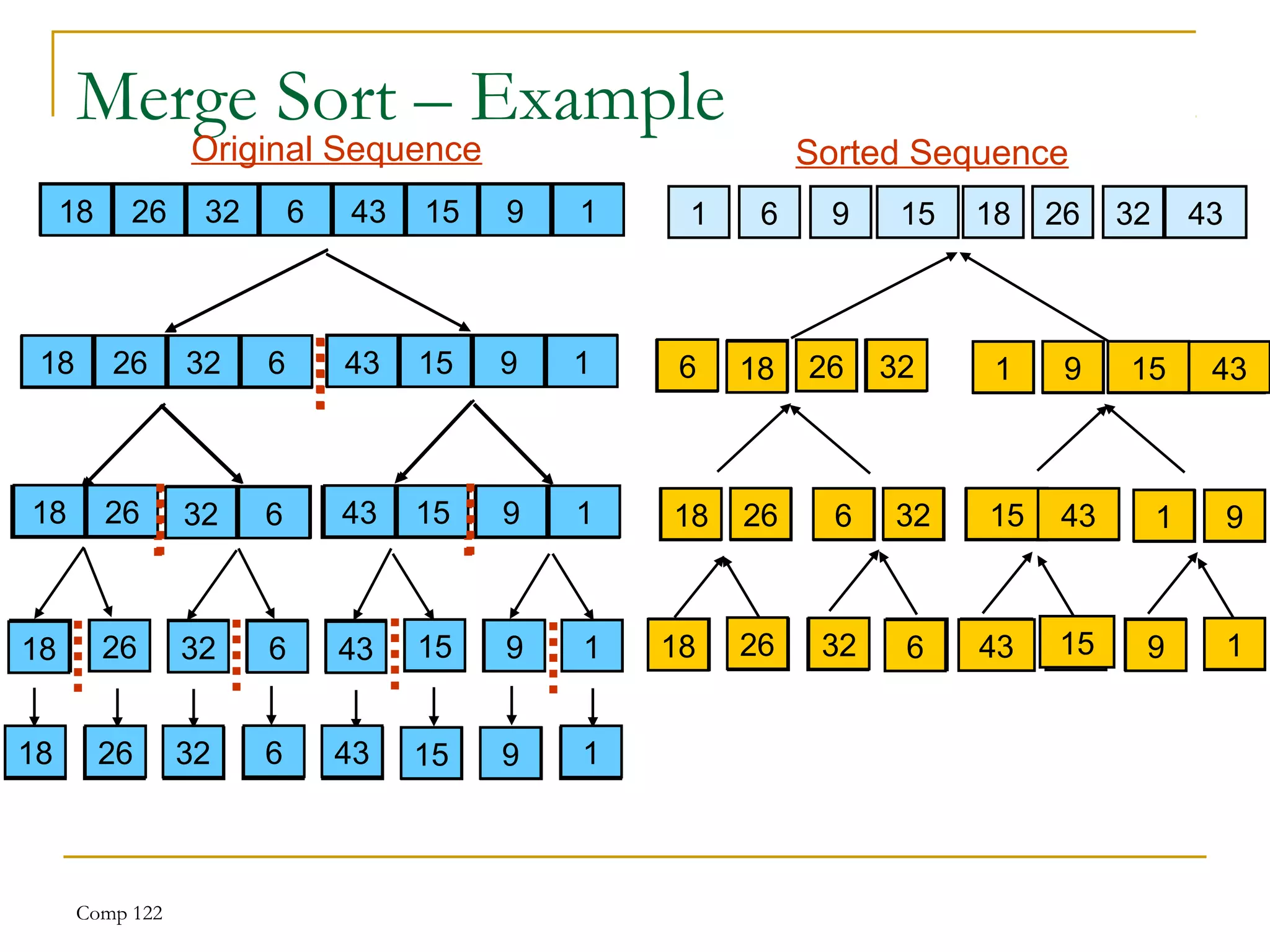
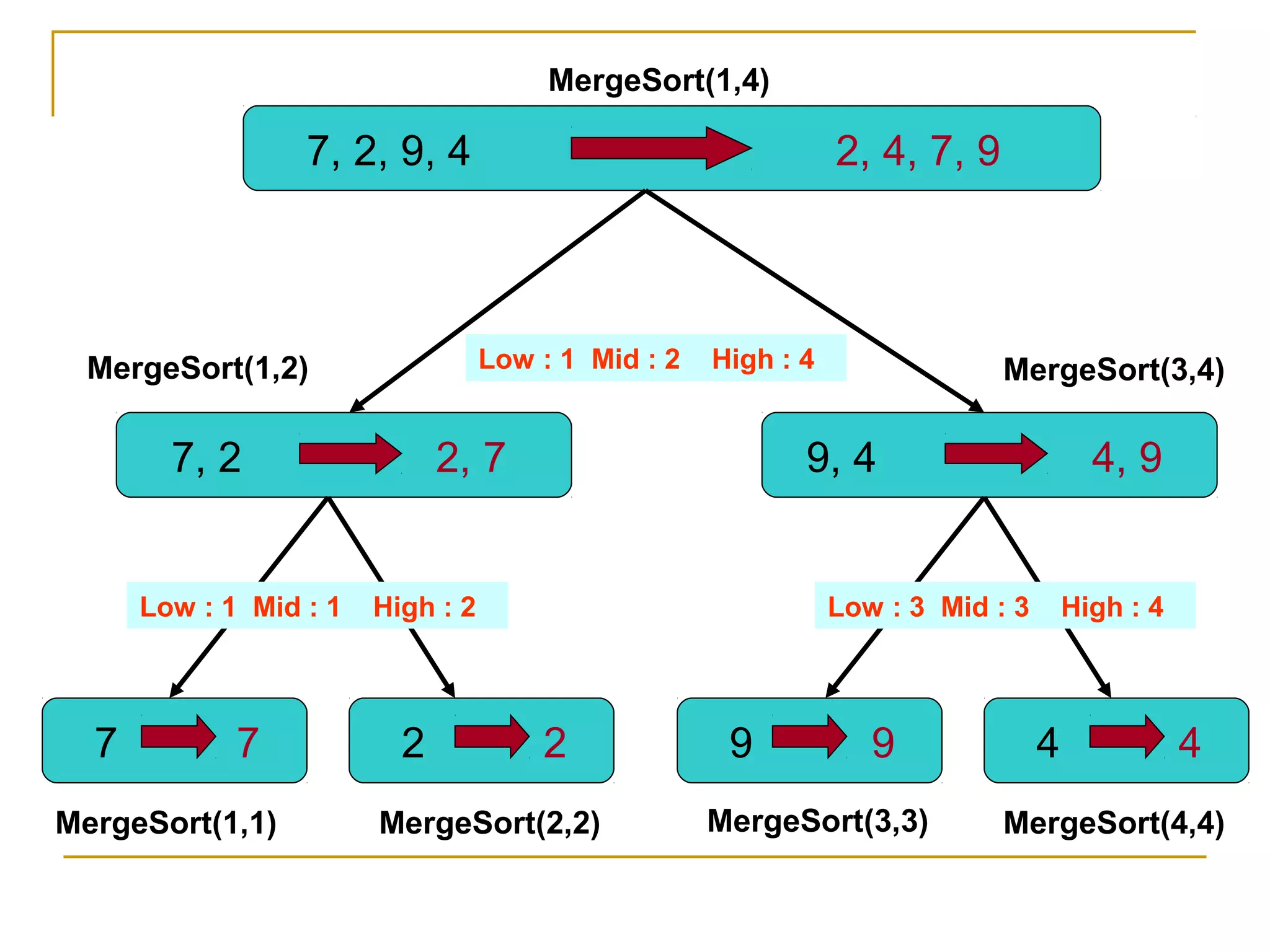
4. Merge Sort :
Suppose an array A with n elements A[1], A[2],
…..,A[n] is in memory. The merge sort algorithm For
sorting A as follows:

Comp 122
Divide and Conquer
 Recursive in structure
 Divide the problem into sub-problems that are
similar to the original but smaller in size
 Conquer the sub-problems by solving them
recursively. If they are small enough, just
solve them in a straightforward manner.
 Combine the solutions to create a solution to
the original problem

Comp 122
An Example: Merge Sort
Sorting Problem: Sort a sequence of n
elements into non-decreasing order.
 Divide: Divide the n-element sequence to be
sorted into two subsequences of n/2
elements each
 Conquer: Sort the two subsequences
recursively using merge sort.
 Combine: Merge the two sorted
subsequences to produce the sorted answer.

Comp 122
Merge Sort – Example
18 26 32 6 43 15 9 1
18 26 32 6 43 15 9 1
18 26 32 6 43 15 9 1
2618 632 1543 19
18 26 32 6 43 15 9 1
18 26 32 6 43 15 9 1
18 26 326 15 43 1 9
6 18 26 32 1 9 15 43
1 6 9 15 18 26 32 43
18 26
18 26
18 26
32
32
6
6
32 6
18 26 32 6
43
43
15
15
43 15
9
9
1
1
9 1
43 15 9 1
18 26 32 6 43 15 9 1
18 26 632
626 3218
1543 19
1 915 43
16 9 1518 26 32 43
Original Sequence Sorted Sequence

MERGESORT(LOW, HIGH)
1. Set LOW := 1.
2. If LOW < HIGH: then:
1. Set MID := (LOW + N)/2
2. Call MERGESORT(LOW, MID)
3. Call MERGESORT(MID+1, HIGH)
4. Call MERGE(LOW,MID,HIGH)
[End of step 2 loop]
7. Exit

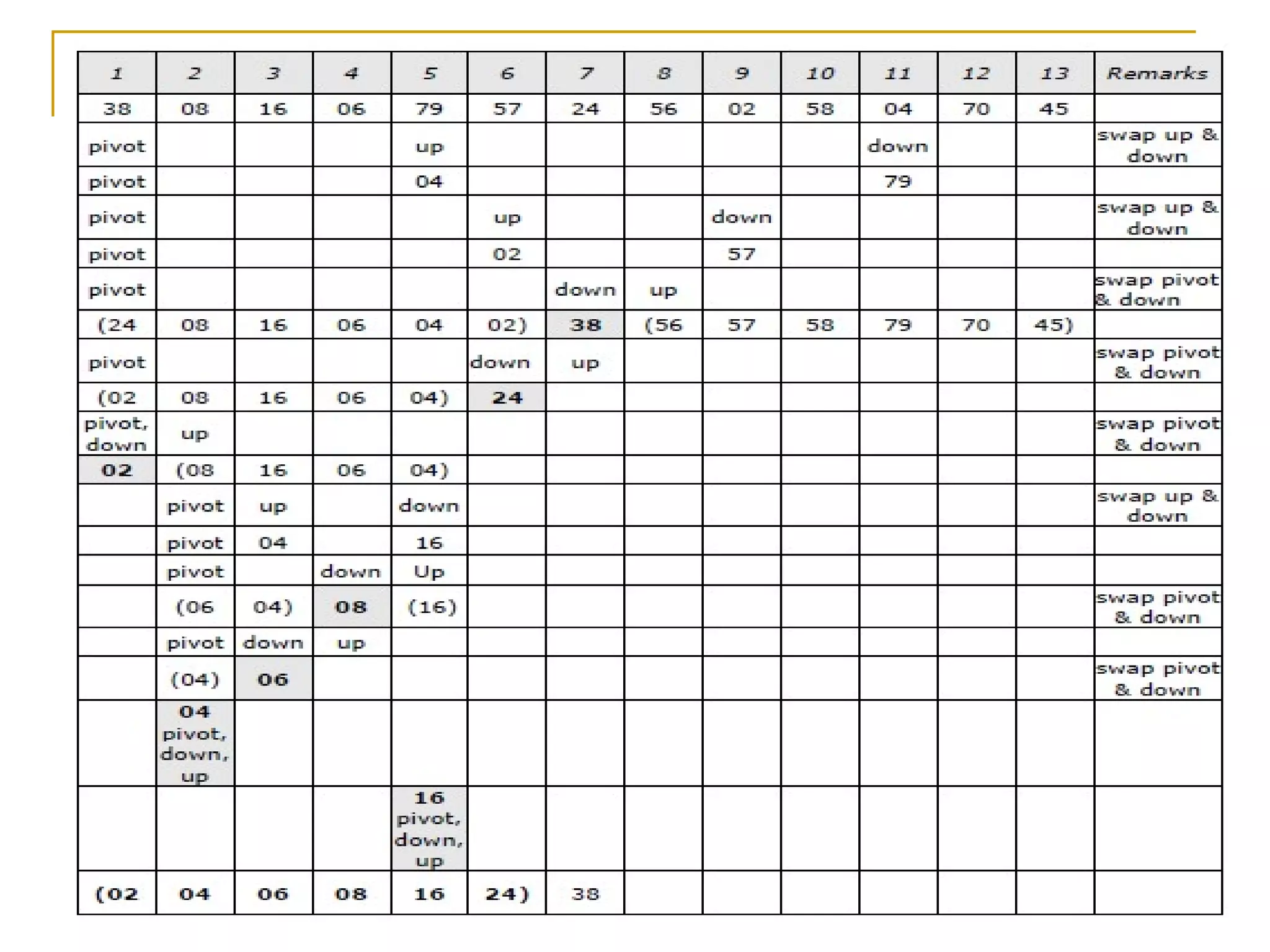
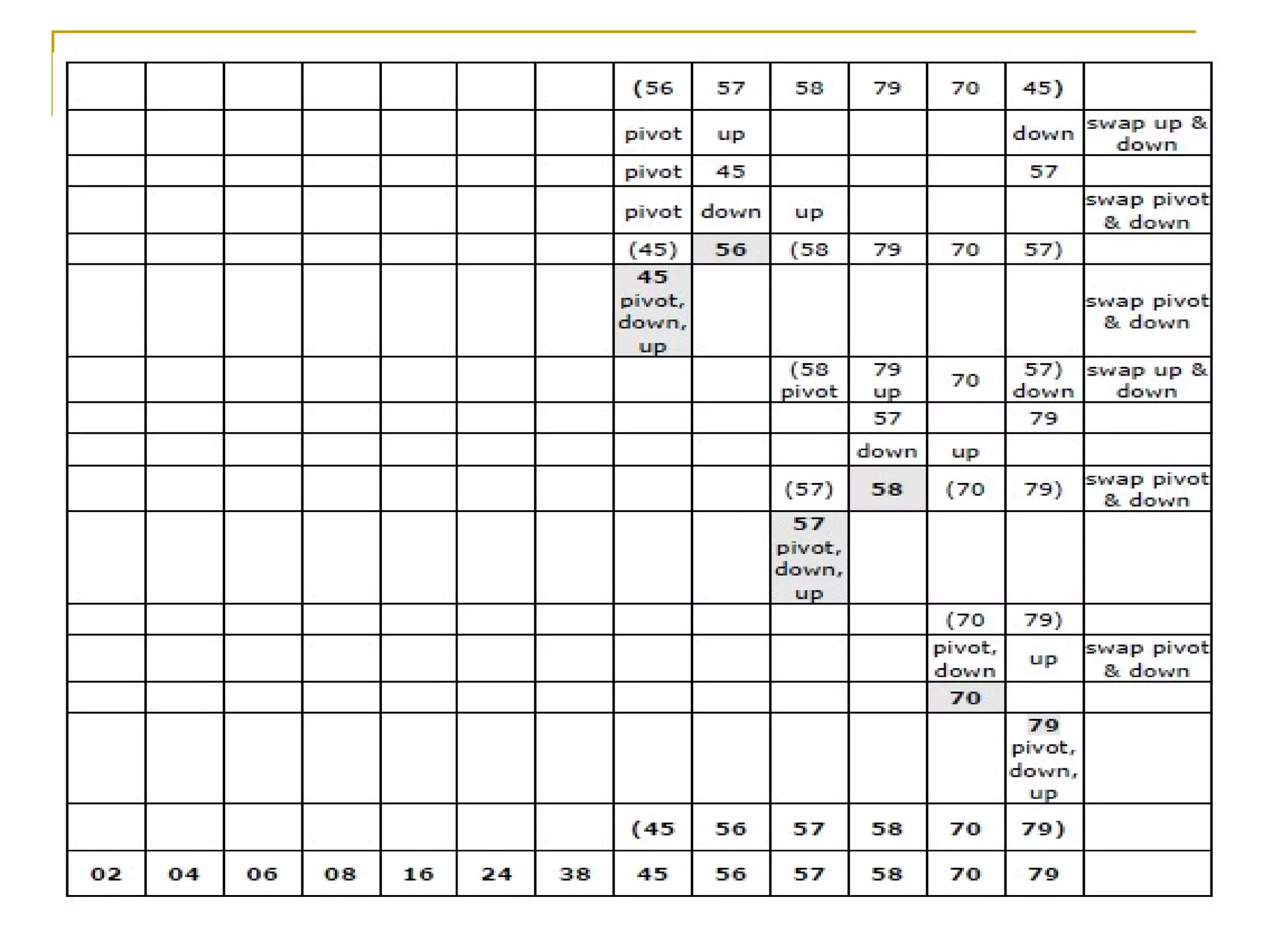
MERGE(A, LOW, MID, HIGH)
This algorithm merges two sorted sub arrays into one
array.
1. [Initialize]
h := LOW, i := LOW, j := MID + 1
2. Repeat while h <= MID && j <= HIGH:
If A[h] <= A[j] then:
Set b[i] := A[h]
Set h := h +1
ELSE:
Set b[i] := A[j]
Set j := j +1
[End of If structure]
Set i := i + 1
[End of loop]

3. If h > MID then:
Set k := j
Repeat while k <= HIGH
Set h[i] := A[k]
Set i := i + 1
ELSE
Set k := h
Repeat while k <= MID
b[i] := a[k];
I := i+1;
4. Set k := LOW
Repeat while k <= HIGH
a[k] := b[k];
5. Return

7 7 2 2 9 9 4 4
Low : 1 Mid : 2 High : 4
Low : 1 Mid : 1 High : 2 Low : 3 Mid : 3 High : 4
7, 2, 9, 4 2, 4, 7, 9
2, 77, 2 9, 4 4, 9
MergeSort(1,2)
MergeSort(1,1) MergeSort(2,2)
MergeSort(1,4)
MergeSort(3,4)
MergeSort(3,3) MergeSort(4,4)

5. Quick Sort :
Quick sort is an algorithm of the divide-and-conquer type. Let us
consider the following example with 13 elements to analyze quick
sort:
Select first element as the pivot element. Move ‘up’ pointer from
left to right in search of an element larger than pivot. Move the
‘down’ pointer from right to left in search of an element smaller
than pivot. If such elements are found, the elements are swapped.
This process continues till the ‘up’ pointer crosses the ‘down’
pointer. If ‘up’ pointer crosses ‘down’ pointer, the position for
pivot is found and interchange pivot and element at ‘down’
position.

Algorithm :
Procedure QUICKSORT (p, q)
integer p, q; global n, A(1:n)
if p < q
then j = q + 1
call PARTITION (p, j)
call QUICKSORT (p, j – 1) // j is the position of
partitioning element
call QUICKSORT (j + 1, q)
endif
End QUICKSORT

Procedure PARTITION (m,p)
integer m, p, i; global A(m:p)
v ← A(m); i ← m //A(m) is the partition element
loop
loop i ← i + 1 until A(i) <= v repeat //i moves left to right
loop p ← p – 1 until A(p) > v repeat //p moves right to left
if i < p
then call INTERCHANGE (A(i), A(p)) //exchange A(i) & A(p)
else exit
endif
repeat
A(m) ← A(p); A(p) ← v //partition element belongs at position p
end PARTITION

Quicksort Algorithm
Given an array of n elements (e.g., integers):
 If array only contains one element, return
 Else
 pick one element to use as pivot.
 Partition elements into two sub-arrays:
 Elements less than or equal to pivot
 Elements greater than pivot
 Quicksort two sub-arrays
 Return results

Example
We are given array of n integers to sort:
40 20 10 80 60 50 7 30 100

Pick Pivot Element
There are a number of ways to pick the pivot element.
In this example, we will use the first element in the
array:
40 20 10 80 60 50 7 30 100

Partitioning Array
Given a pivot, partition the elements of the array
such that the resulting array consists of:
1. One sub-array that contains elements >= pivot
2. Another sub-array that contains elements < pivot
The sub-arrays are stored in the original data
array.
Partitioning loops through, swapping elements
below/above pivot.

40 20 10 80 60 50 7 30 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i j

40 20 10 80 60 50 7 30 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i j
1. While data[i] <= data[pivot]
++i

40 20 10 80 60 50 7 30 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i j
++i
2. While data[j] > data[pivot]
--j

40 20 10 80 60 50 7 30 100pivot_index = 0
[0] [1] [2] [3] [4] [5] [6] [7] [8]
i j
++i
--j
3. If i < j
swap data[i] and data[j]

40 20 10 30 60 50 7 80 100pivot_index = 0
i j
++i
--j
3. If i < j
[0] [1] [2] [3] [4] [5] [6] [7] [8]

40 20 10 30 60 50 7 80 100pivot_index = 0
i j
++i
--j
3. If i < j
4. While j > i, go to 1.
[0] [1] [2] [3] [4] [5] [6] [7] [8]

++i
--j
3. If i < j
40 20 10 30 7 50 60 80 100pivot_index = 0
i j
[0] [1] [2] [3] [4] [5] [6] [7] [8]

++i
--j
3. If i < j
5. Swap data[j] and data[pivot_index]
40 20 10 30 7 50 60 80 100pivot_index = 0
i j
[0] [1] [2] [3] [4] [5] [6] [7] [8]

++i
--j
3. If i < j
5. Swap data[j] and data[pivot_index]
7 20 10 30 40 50 60 80 100pivot_index = 4
i j
[0] [1] [2] [3] [4] [5] [6] [7] [8]

Partition Result
7 20 10 30 40 50 60 80 100
<= data[pivot] > data[pivot]
[0] [1] [2] [3] [4] [5] [6] [7] [8]

Recursion: Quicksort Sub-arrays
7 20 10 30 40 50 60 80 100
<= data[pivot] > data[pivot]
[0] [1] [2] [3] [4] [5] [6] [7] [8]

6. Radix Sort :
Radix sort is a method can be used to sort a list of names
alphabetically. To sort alphabetically radix is 26, the 26 letters of
the alphabet.
In radix sort, if numbers are present then,
In first pass, the numbers are sorted according to the units digits.
In second pass, the numbers are sorted according to the tens digit.
In third pass, the numbers are sorted according to the hundreds
digits. & so on.

Suppose 9 numbers are as follows:
348, 143, 361, 423, 538, 128, 321, 543, 366
The numbers would be sorted in three phases,
First Pass
Input 0 1 2 3 4 5 6 7 8 9
348 348
143 143
361 361
423 423
538 538
128 128
321 321
543 543
366 366

Second Pass
Input 0 1 2 3 4 5 6 7 8 9
361 361
321 321
143 143
423 423
543 543
366 366
348 348
538 538
128 128

Third Pass
Input 0 1 2 3 4 5 6 7 8 9
321 321
423 423
128 128
538 538
143 143
543 543
348 348
361 361
366 366

When numbers are collected after the third pass, the numbers are
in the following order:
128, 143, 321, 348, 361, 366, 423, 538, 543
Thus, the numbers are sorted.

radix_sort(int arr[], int n)
{
int bucket[10][5],buck[10],b[10];
int i,j,k,l,num,div,large,passes;
div=1;
num=0;
large=arr[0];
for(i=0 ; i< n ; i++)
{
if(arr[i] > large)
{
large = arr[i];
}
while(large > 0)
{
num++;
large = large/10;
}
for(passes=0 ; passes < num ;
passes++)
{
for(k=0 ; k< 10 ; k++)
{
buck[k] = 0;
}
for(i=0 ; i< n ;i++)
{
l = ((arr[i]/div)%10);
bucket[l][buck[l]++] = arr[i];
}
i=0;
for(k=0 ; k < 10 ; k++)
{
for(j=0 ; j < buck[k] ; j++)
{
arr[i++] = bucket[k][j];
}
}
div*=10;
}}}

7. Heap Sort :
Consider, the following elements,
3, 1, 4, 2, 5
For sorting given array we first create Heap tree,
3
1 4
2 5
3
5 4
2 1
5
3 4
2 1
Max-Heap

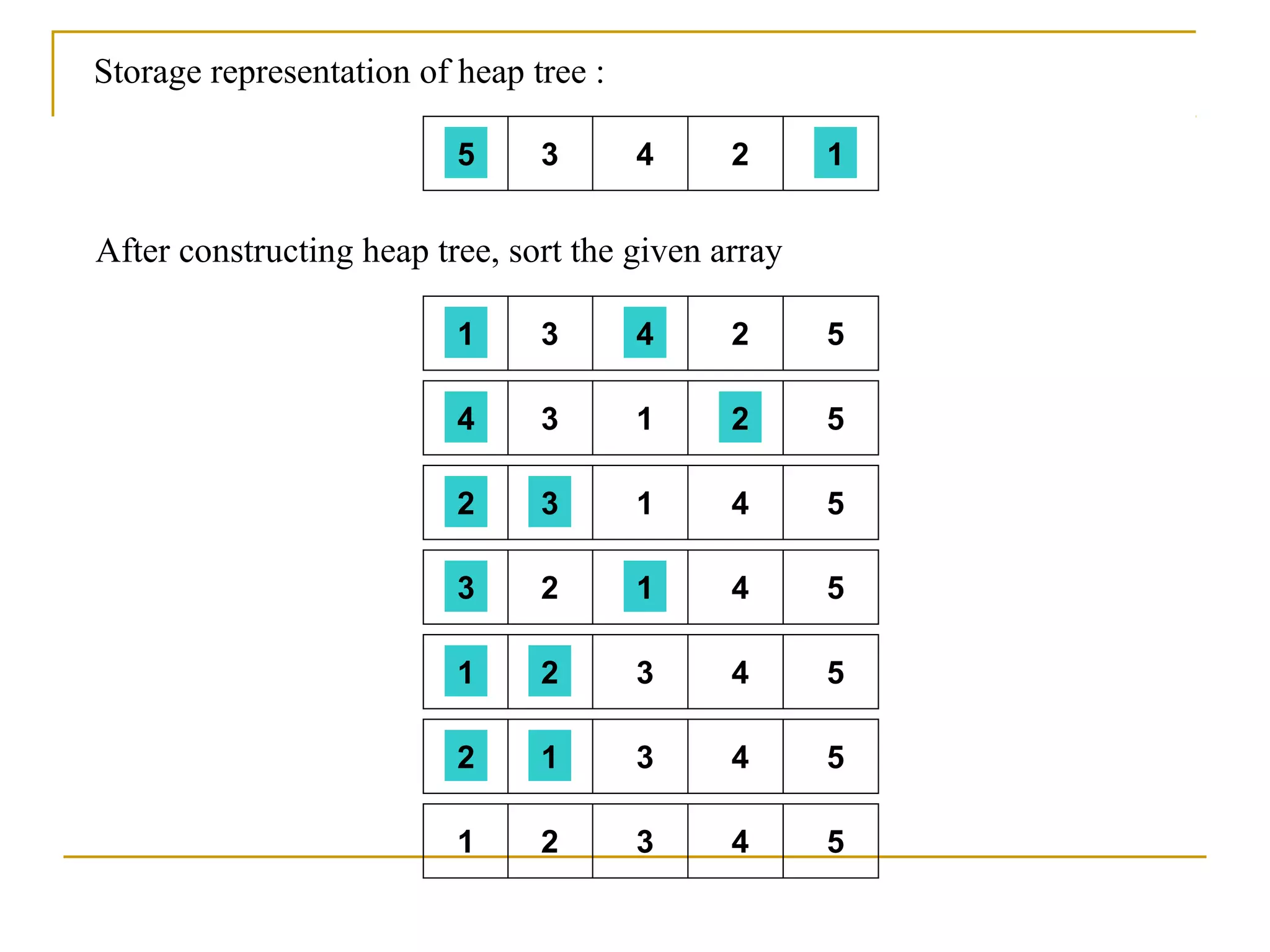
5 3 4 2 1
Storage representation of heap tree :
After constructing heap tree, sort the given array
1 3 4 2 5
4 3 1 2 5
2 3 1 4 5
3 2 1 4 5
1 2 3 4 5
2 1 3 4 5
1 2 3 4 5

Searching:
Searching is used to find the location where an element is
available. There are two types of search techniques. They are:
1.Linear or sequential search
This is the simplest of all searching techniques.
In this technique, an ordered or unordered list will be
searched one by one from the beginning until the
desired element is found.
If the desired element is found in the list then the search
is successful otherwise unsuccessful.

Suppose there are ‘n’ elements organized sequentially on a
List.
The number of comparisons required to retrieve an element
from the list, purely depends on where the element is stored in
the list.
If it is the first element, one comparison will do; if it is second
element two comparisons are necessary and so on.
On an average you need [(n+1)/2] comparison’s to search an
element.
If search is not successful, you would need ’n’ comparisons.

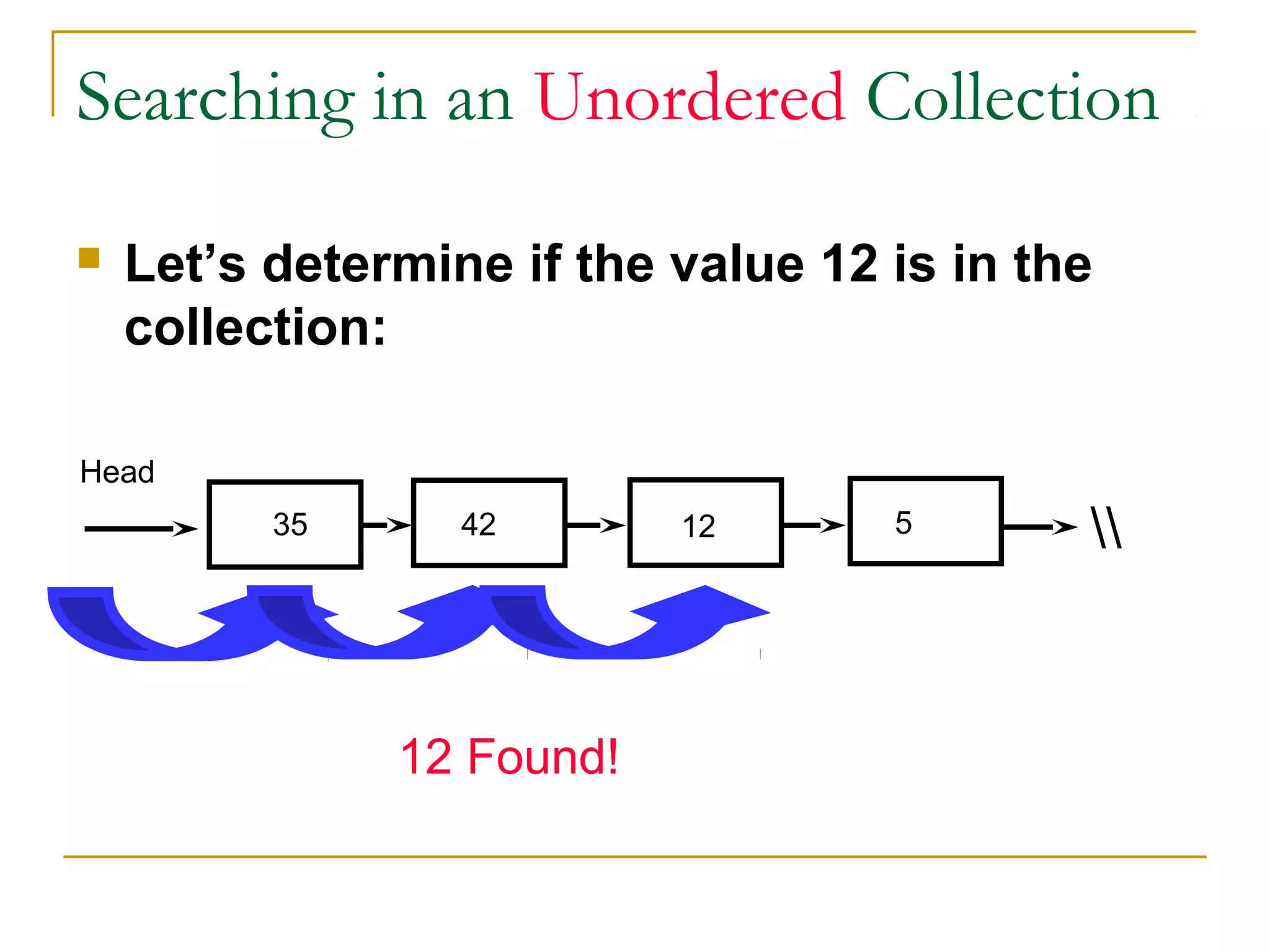
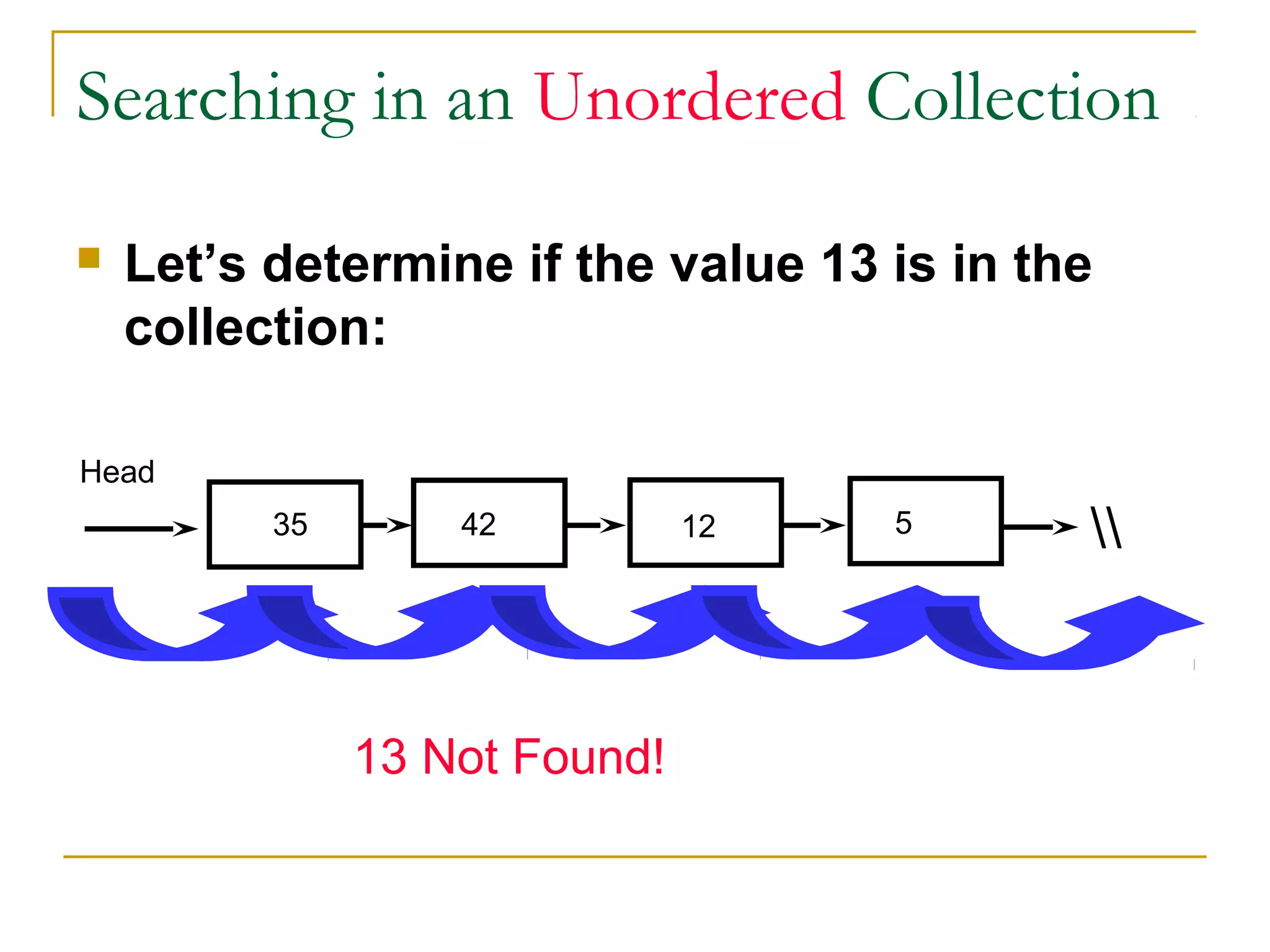
Algorithm
Linear Search ( Array A, Value x)
Step 1: Set i to 1
Step 2: if i > n then go to step 7
Step 3: if A[i] = x then go to step 6
Step 4: Set i to i + 1
Step 5: Go to Step 2
Step 6: Print Element x Found at index i and go to step 8
Step 7: Print element not found
Step 8: Exit

Searching in an Unordered Collection
 Let’s determine if the value 12 is in the
collection:
35 42 12 5
12 Found!
Head

Searching in an Unordered Collection
collection:
35 42 12 5
13 Not Found!
Head

Searching in an Ordered Collection
collection:
5 12 35 42
13 Not Found!
Head

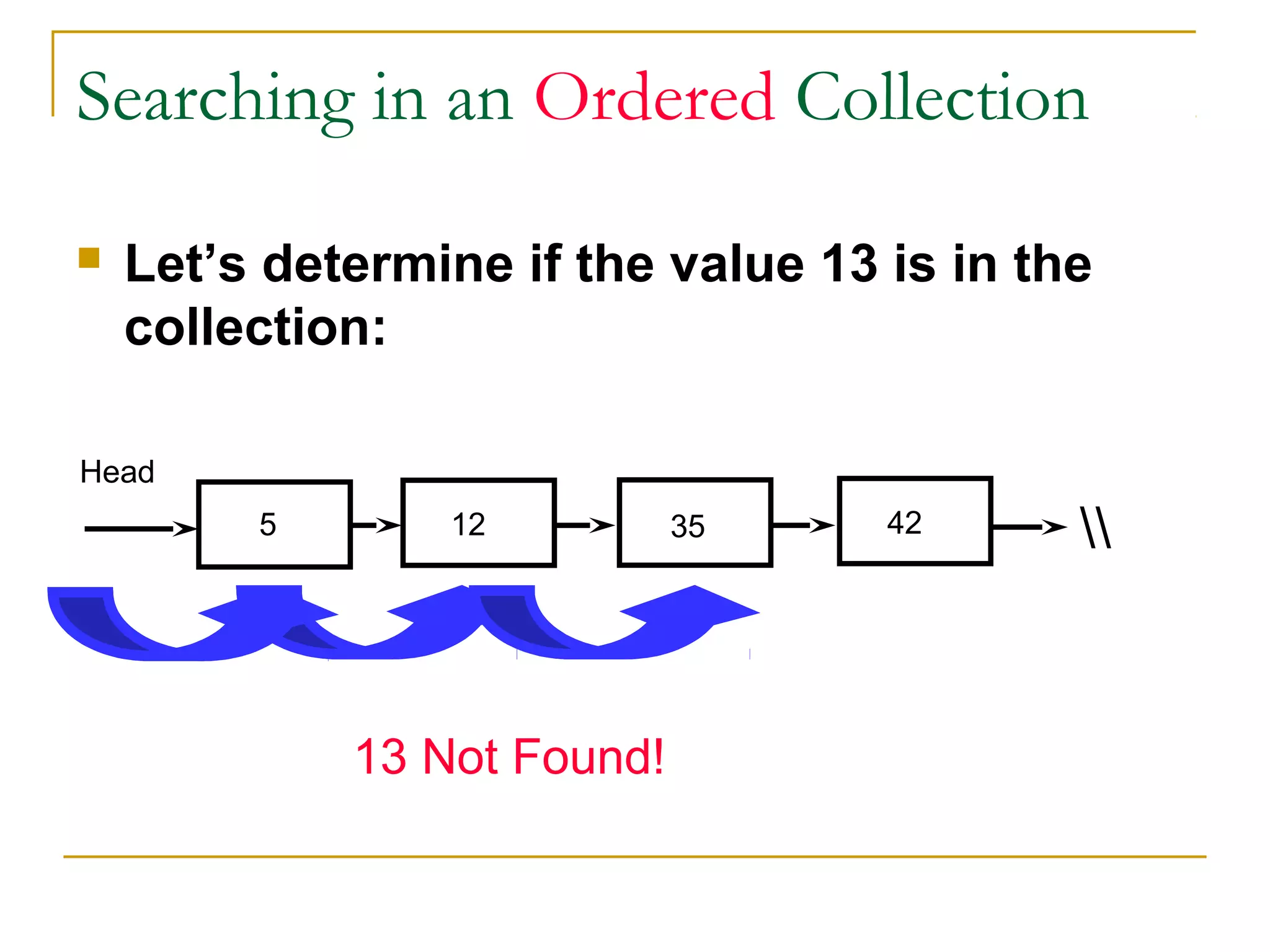
2. BINARY SEARCH
If we have ‘n’ records which have been ordered by keys so that
x1 < x2 < … < xn .
When we are given a element ‘x’, binary search is used to find
the corresponding element from the list.
In case ‘x’ is present, we have to determine a value ‘j’ such that
a[j] = x(successful search).
If ‘x’ is not in the list then j is to set to zero (un successful
search).

In Binary search we jump into the middle of the file, where we
find key a[mid], and compare ‘x’ with a[mid]. If x = a[mid] then
the desired record has been found.
If x < a[mid] then ‘x’ must be in that portion of the file that
precedes a[mid].
Similarly, if a[mid] > x, then further search is only necessary in
that part of the file which follows a[mid].

Procedure BINSRCH(A, n, x, j)
//given an array A(1:n) of elements in non decreasing order.
//n>=0, determine if x is present, and if so, set j such that
x=A(j)
// else j=0.
integer low, mid, high, j, n;
low ← 1; high ← n
while low <= high do
mid ← (low + high)/2
case
: x < A(mid) : high ← mid – 1
: x > A(mid) : low ← mid + 1
: else : j ← mid; return
endcase
repeat
j ← 0
end BINSRCH

Binary search (Example)
 Example: Searching the array below for the value 42:
inde
x
0 1 2 3 4 5 6 7 8 9 1
0
1
1
1
2
1
3
1
4
1
5
16
valu
e
-4 2 7 1
0
1
5
2
0
2
2
2
5
3
0
3
6
4
2
5
0
5
6
6
8
8
5
9
2
10
3
min mid max
Check A[mid]== number If yes PRINT
Check number<A[mid]
Check number>A[mid]
If yes min=mid+1
and repeat
If yes max=mid-1
and repeat

Unit 7 sorting

More Related Content

What's hot

Similar to Unit 7 sorting

More from kalyanineve

Recently uploaded

Unit 7 sorting