The document discusses various sorting algorithms:
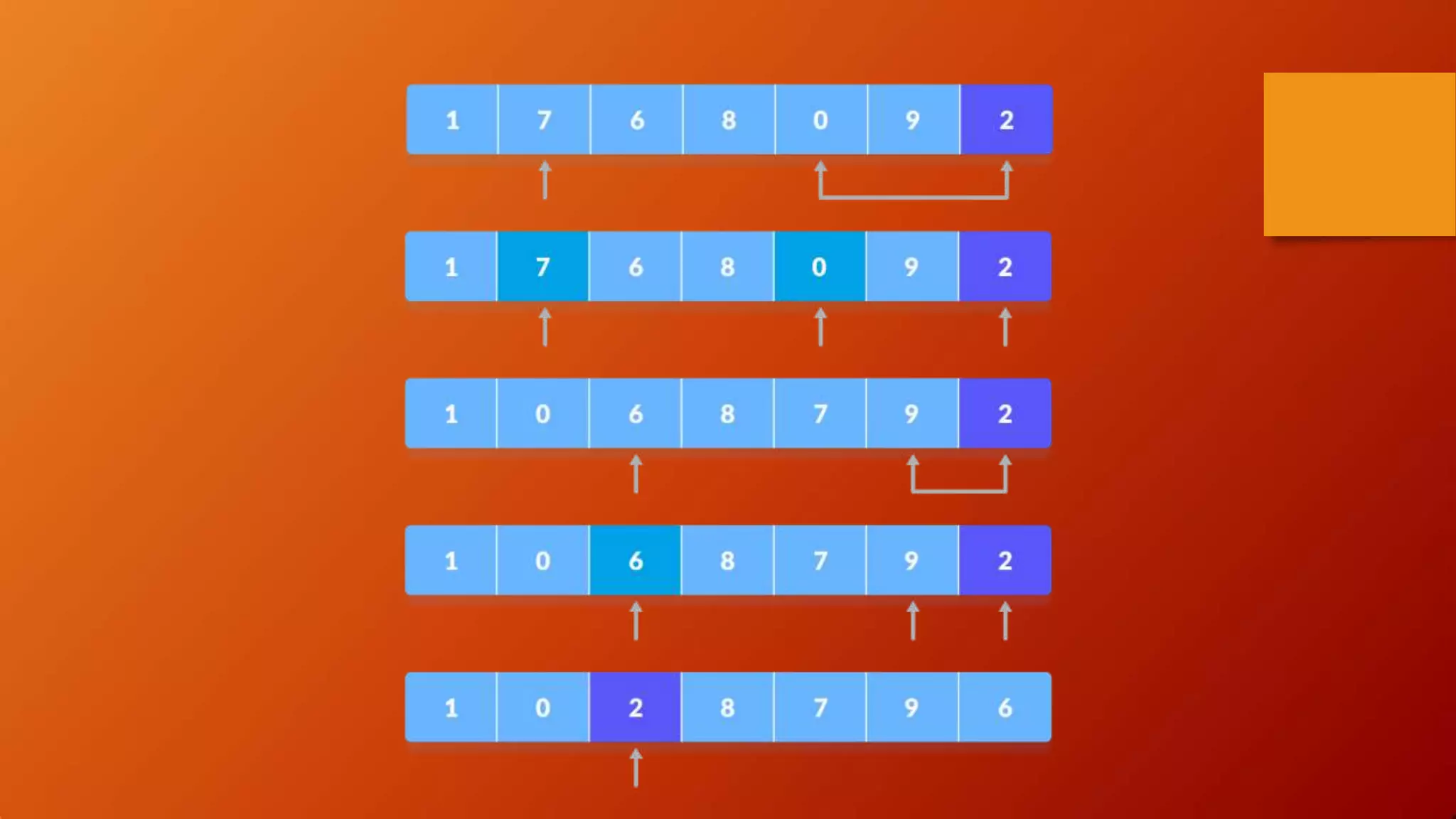
- Insertion sort works by dividing an array into sorted and unsorted parts, inserting unsorted elements into the sorted part one by one.
- Quicksort uses a divide and conquer approach, recursively dividing the array into sublists and selecting a pivot element.
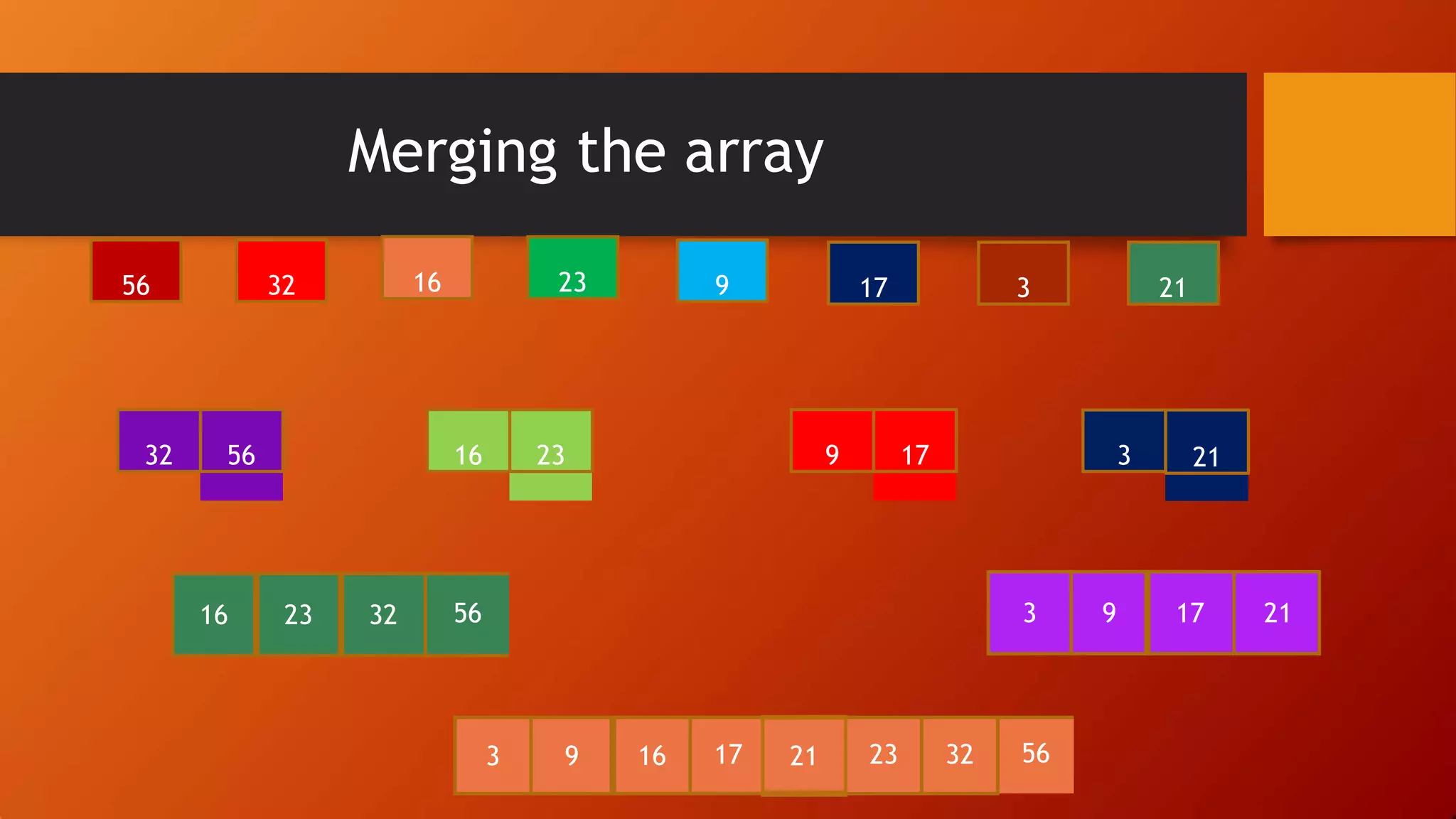
- Merge sort divides the array into halves, recursively sorts the halves, and then merges the sorted halves.
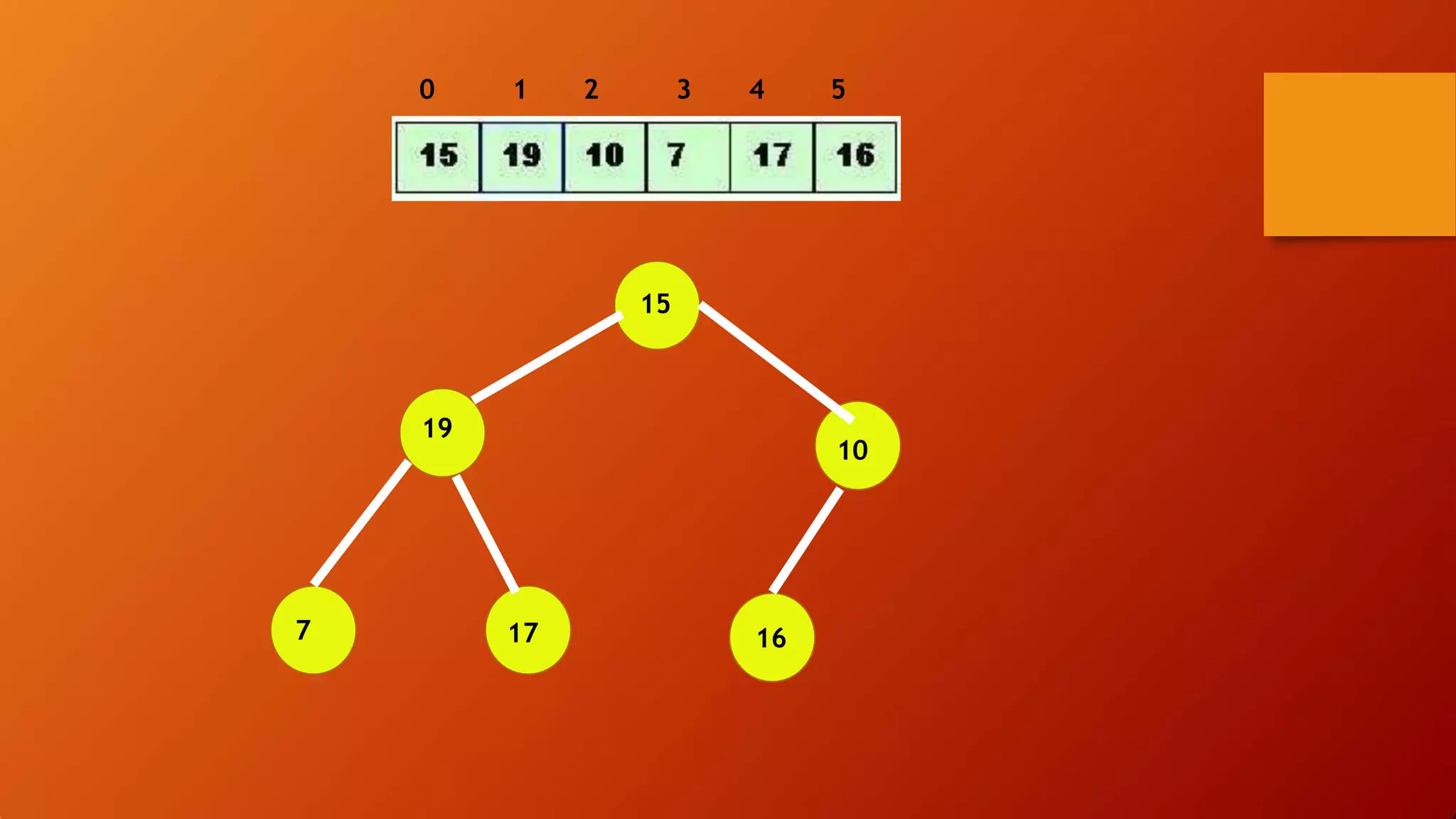
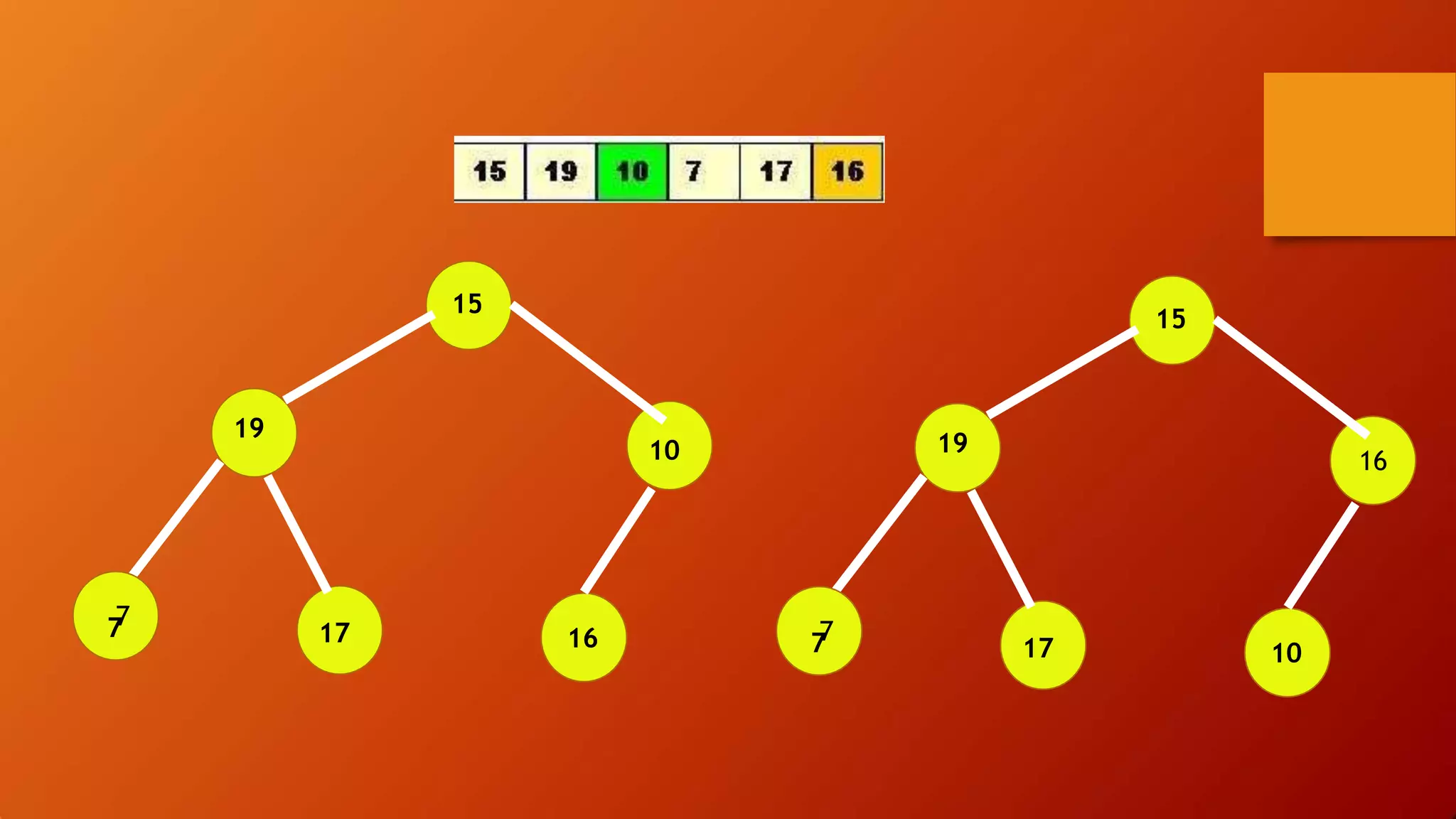
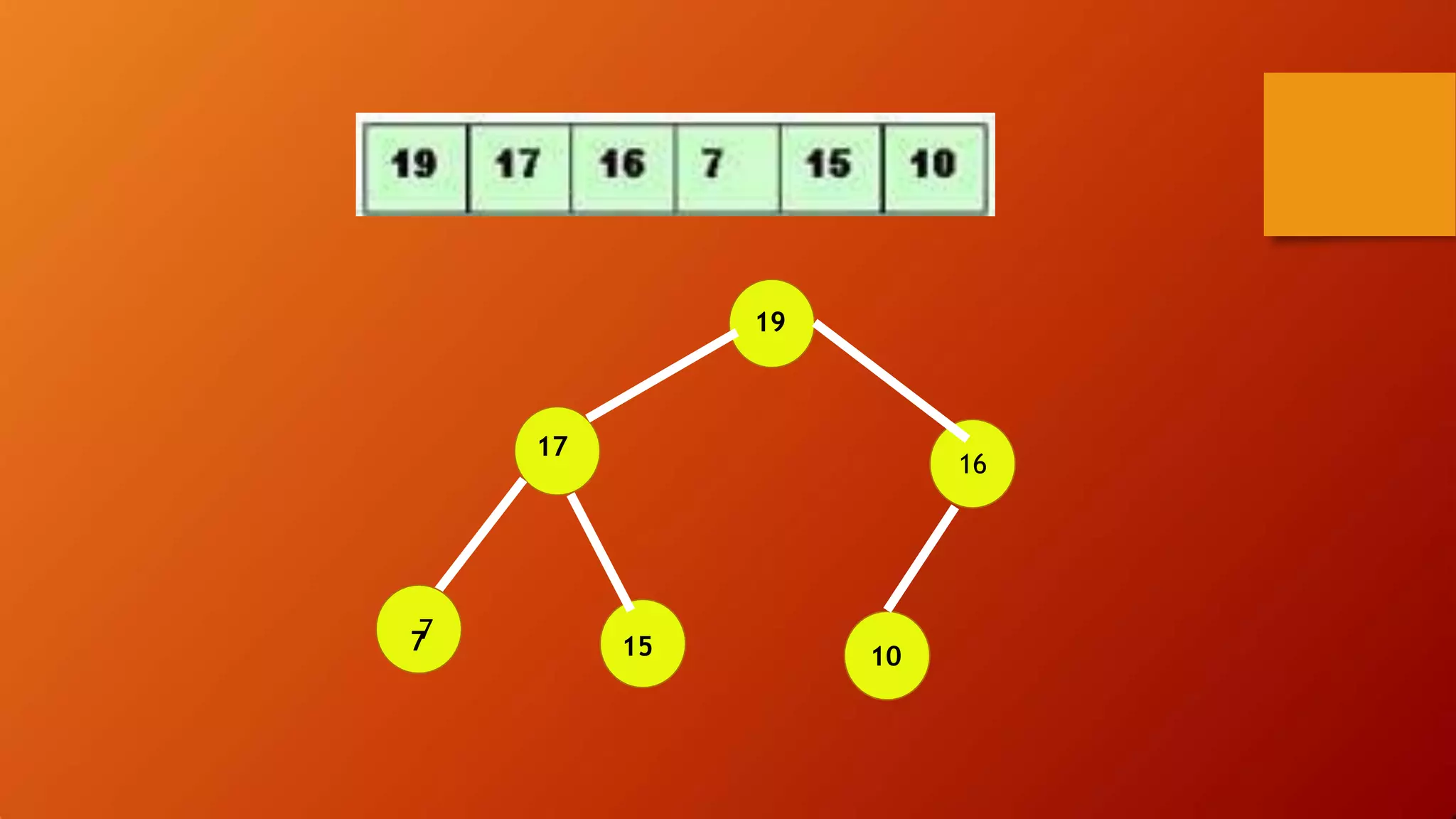
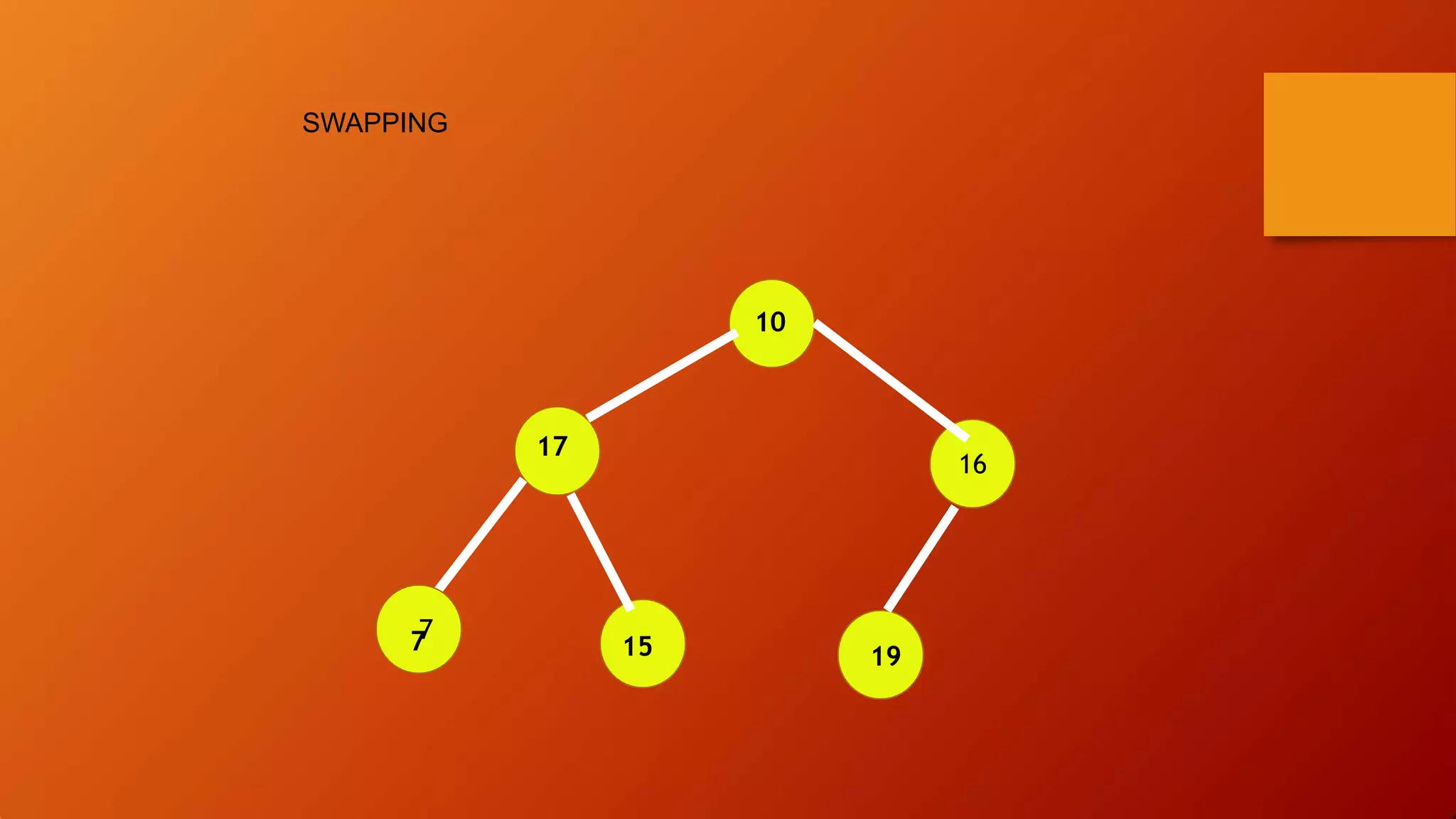
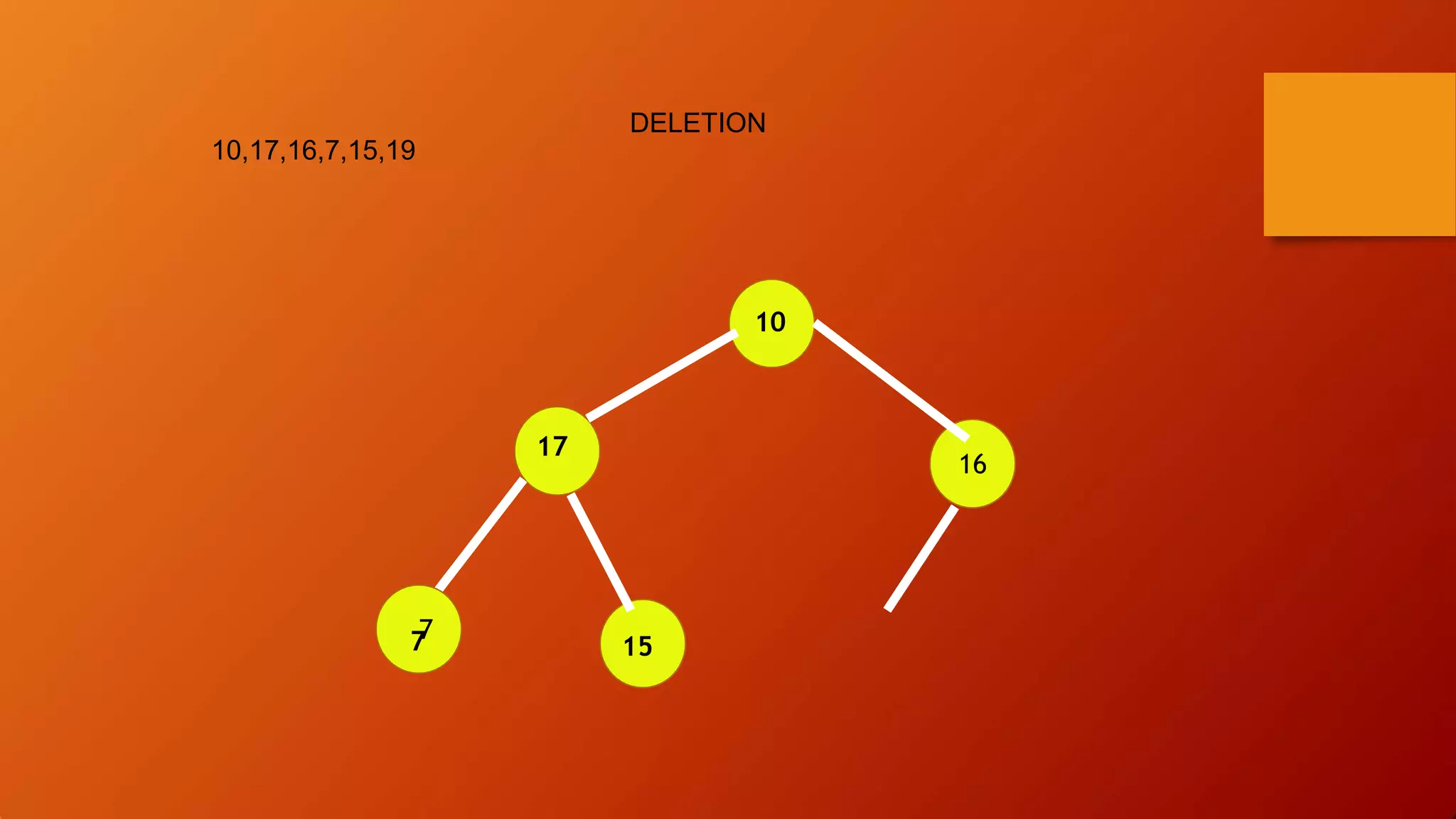
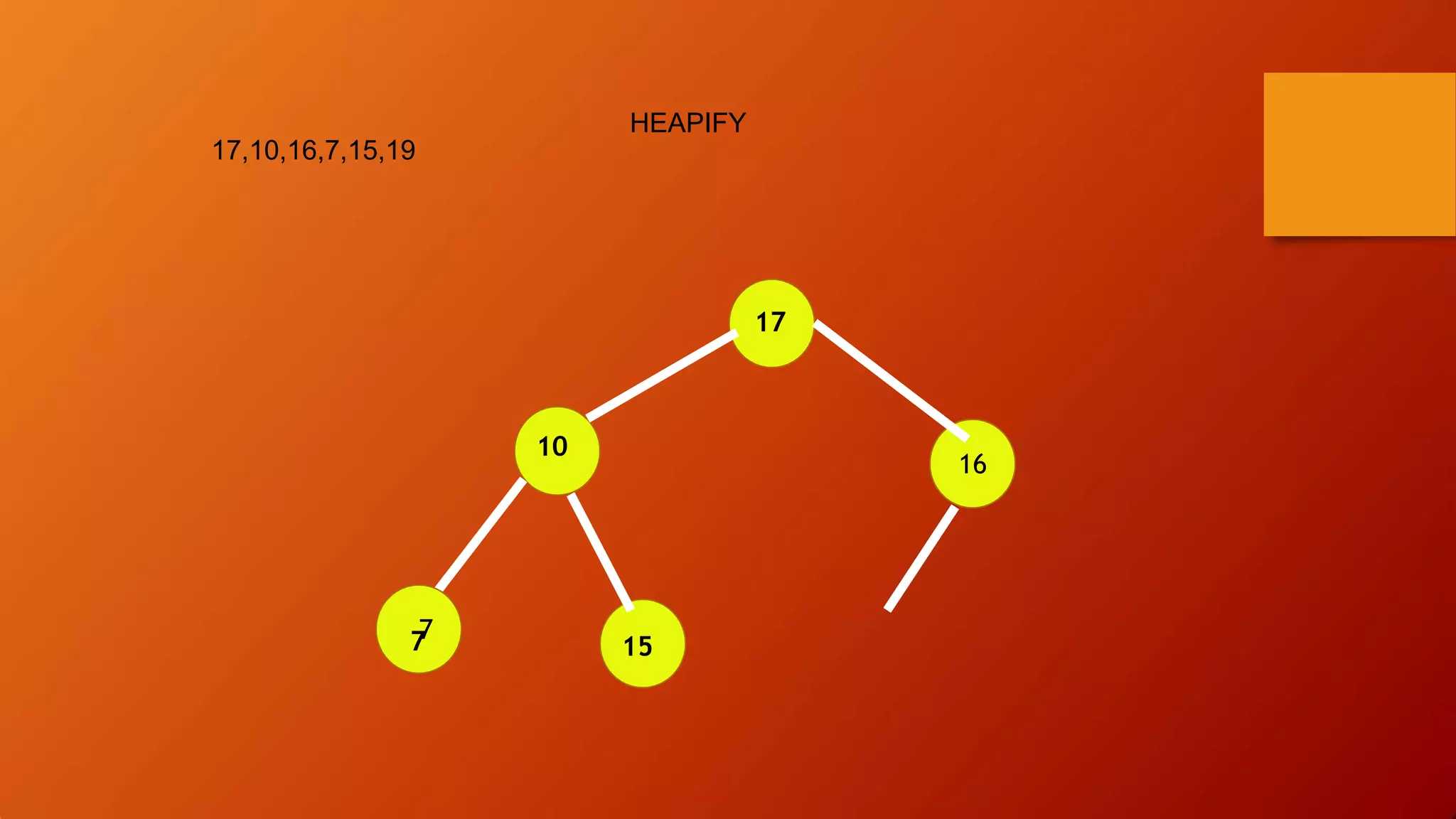
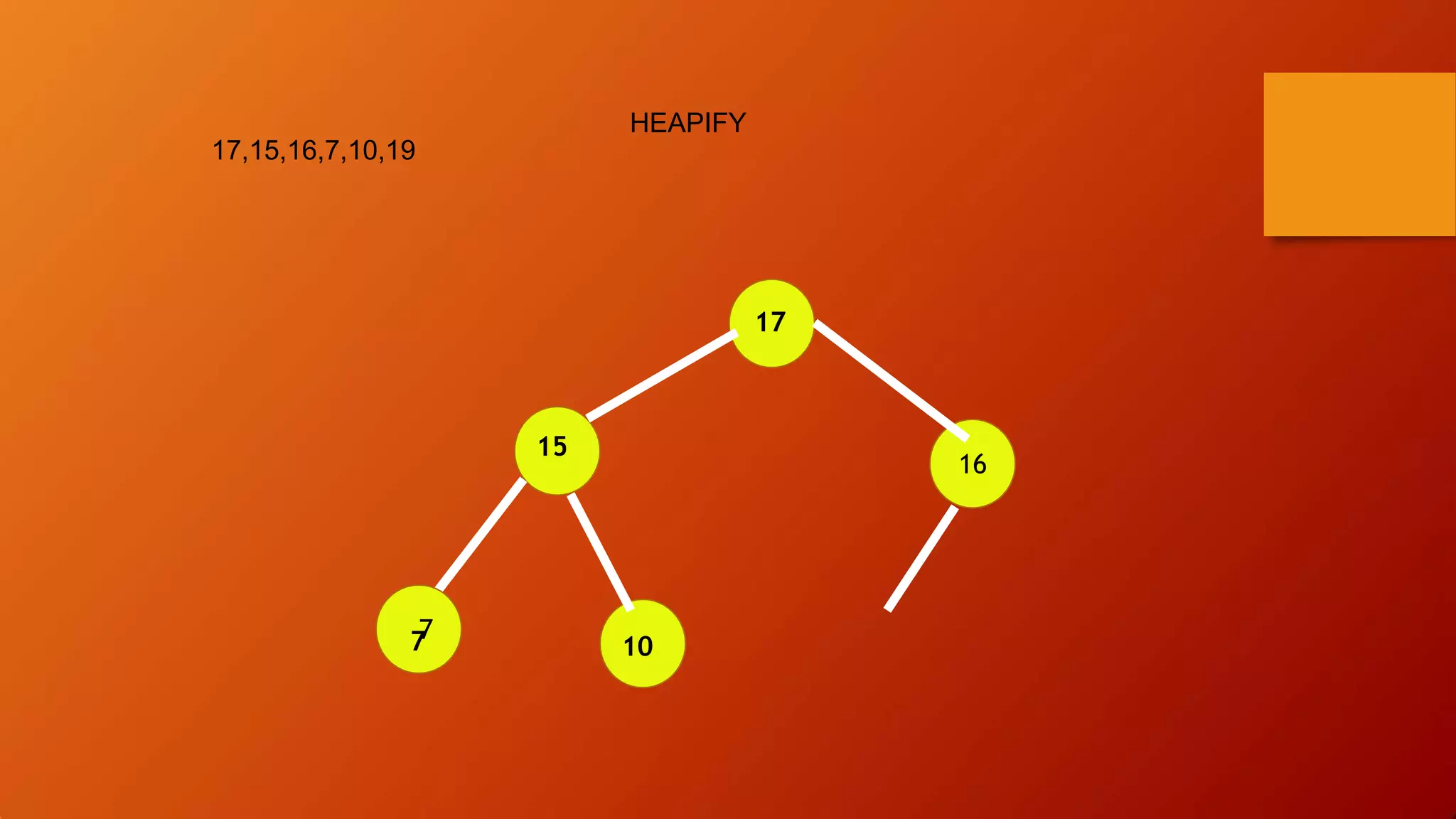
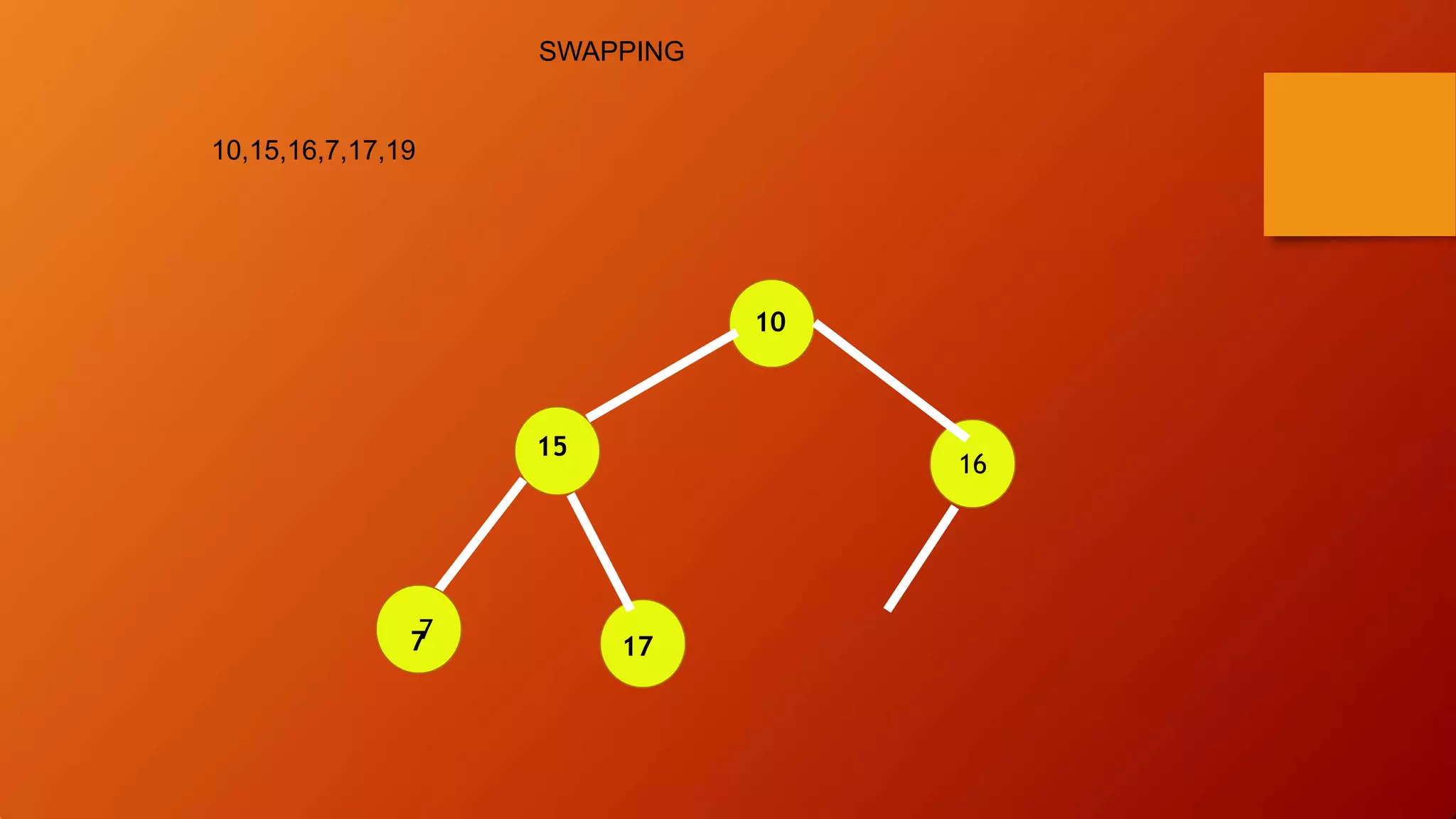
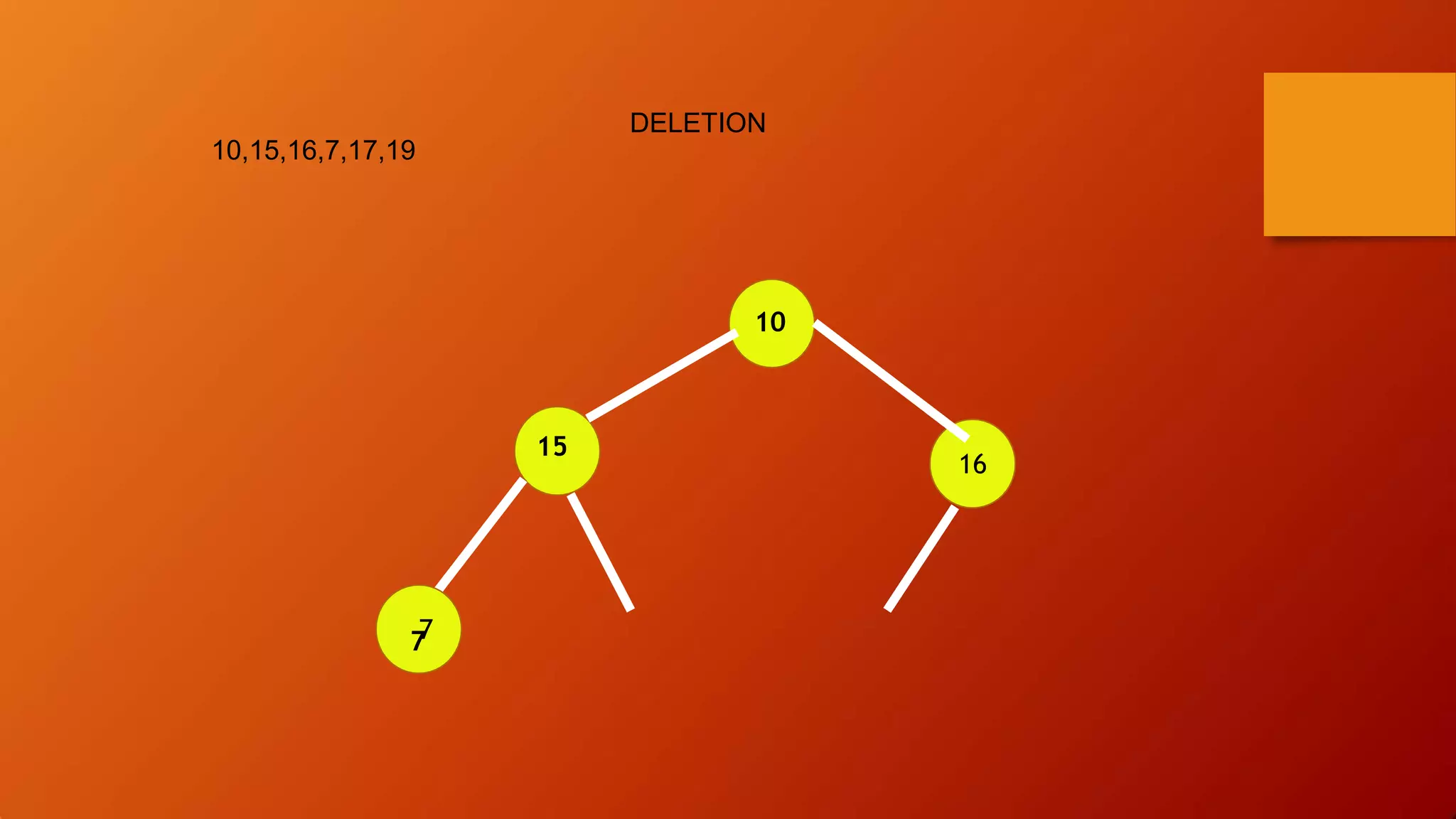
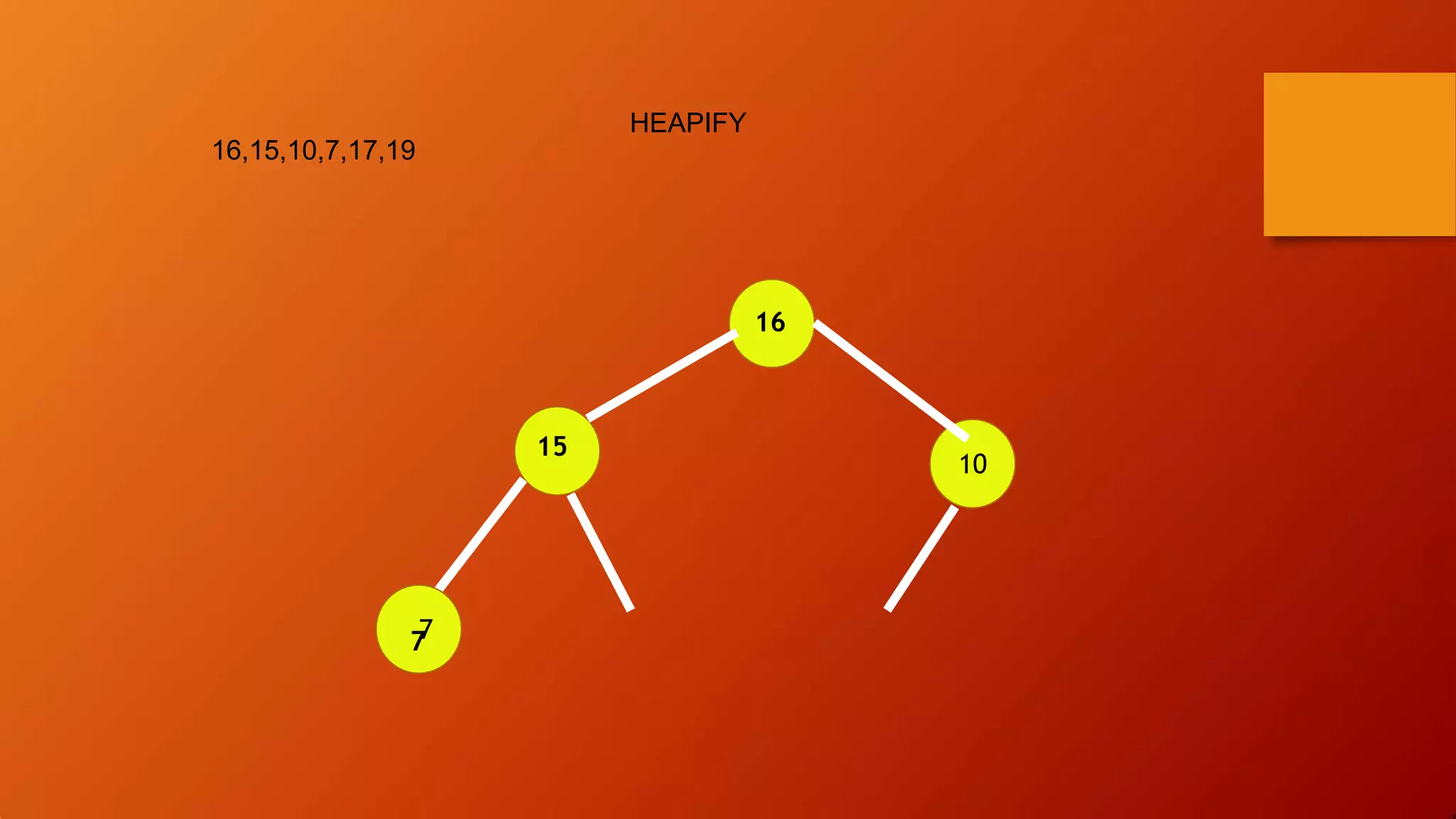
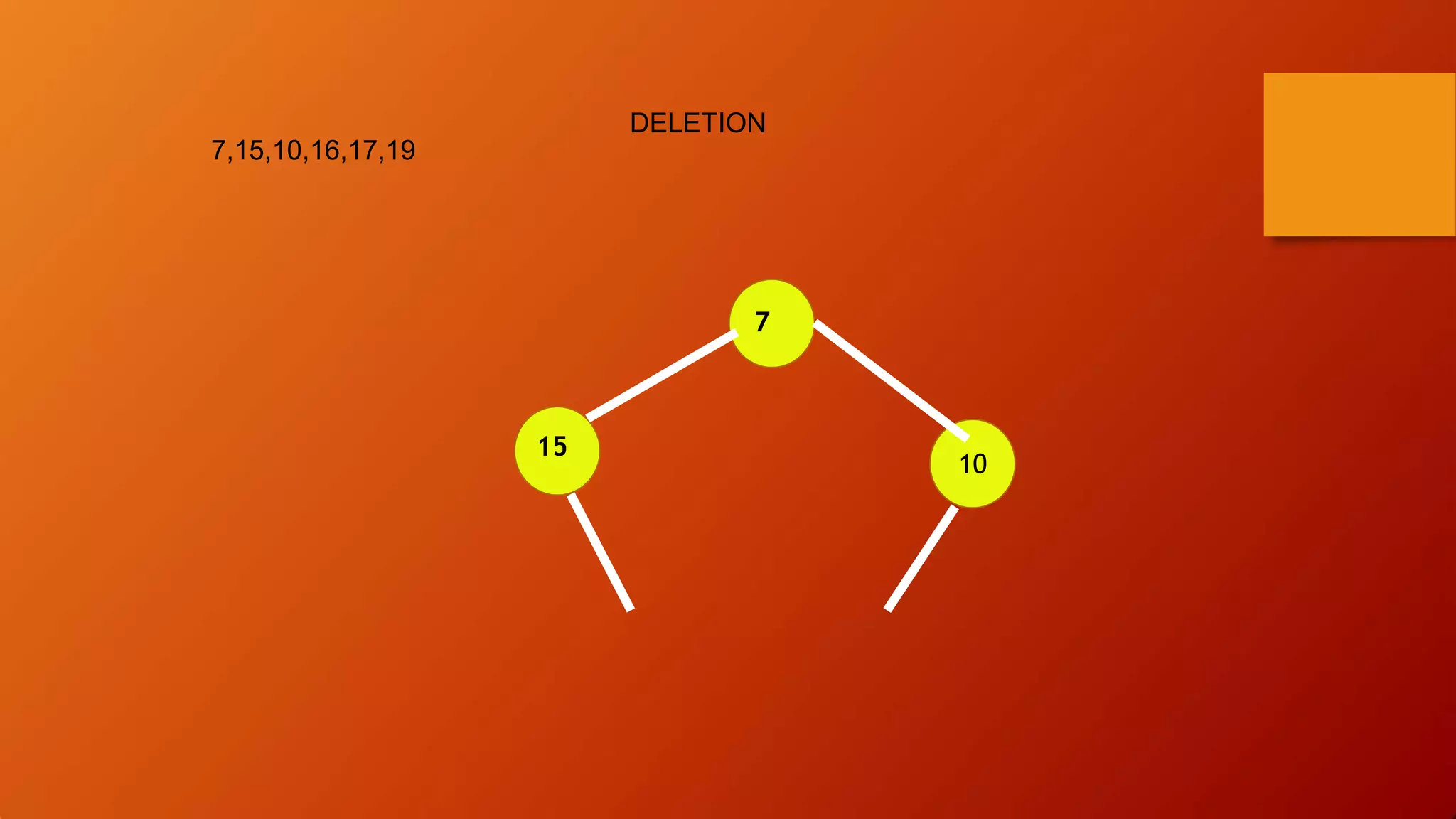
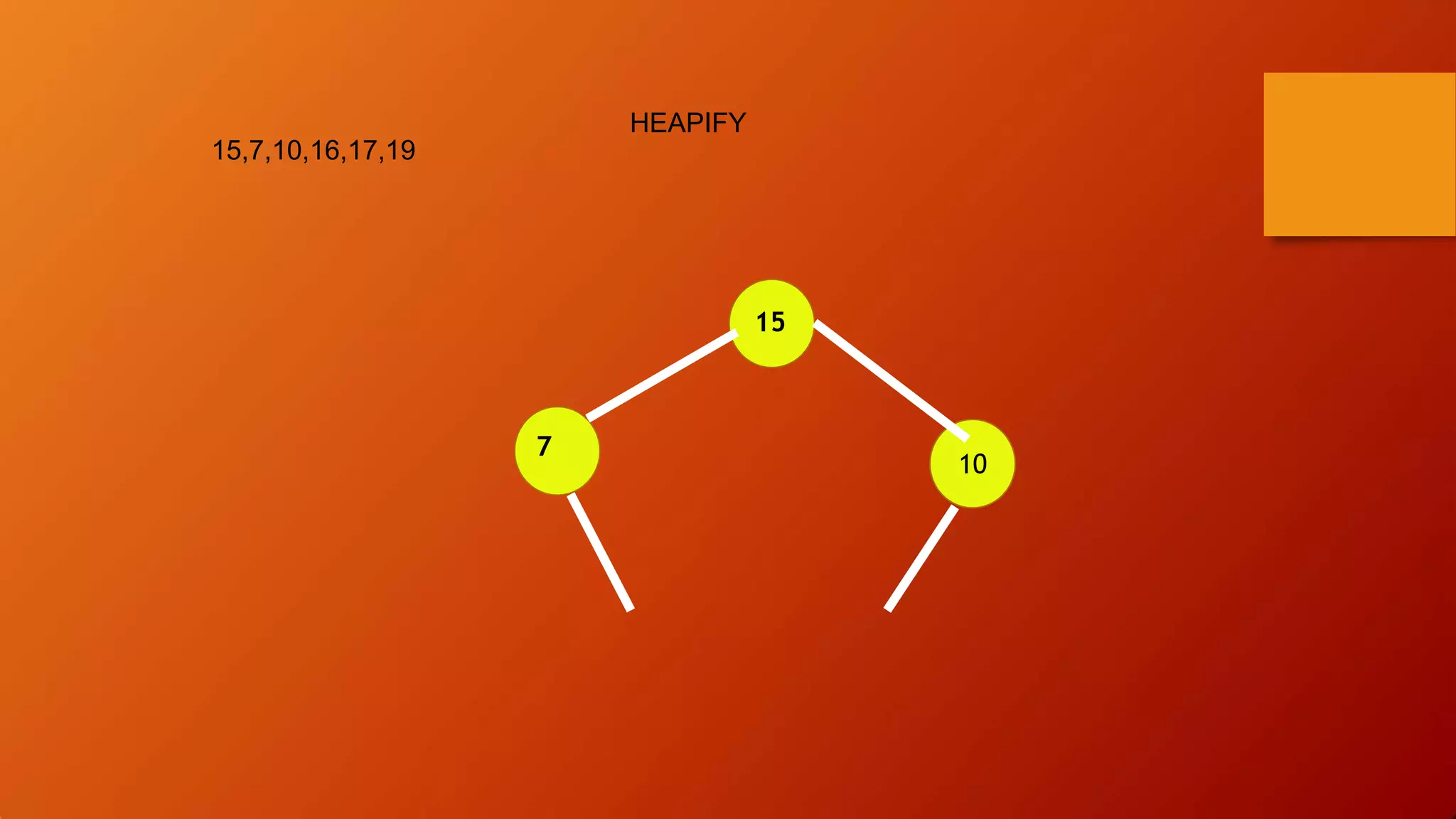
- Heap sort uses a heap data structure that maintains the heap property as it builds the heap from an unsorted array and then extracts elements in sorted order.


































![MAX-HEAP PROPERTY
Each node in a tree has a key which is
less than or equal to the key of its parent.
A[PARENTi] >= A[i]
“While using this property it makes a list of
descending order.”](https://image.slidesharecdn.com/sortingalgorithms-200423045225/75/Sorting-algorithms-in-Data-Structure-37-2048.jpg)
![MIN-HEAP PROPERTY
Each node in a tree has a key which is
greater than or equal to the key of
its parent.
A[PARENTi] <= A[i]
“While using this property it makes a list of
ascending order.”](https://image.slidesharecdn.com/sortingalgorithms-200423045225/75/Sorting-algorithms-in-Data-Structure-38-2048.jpg)