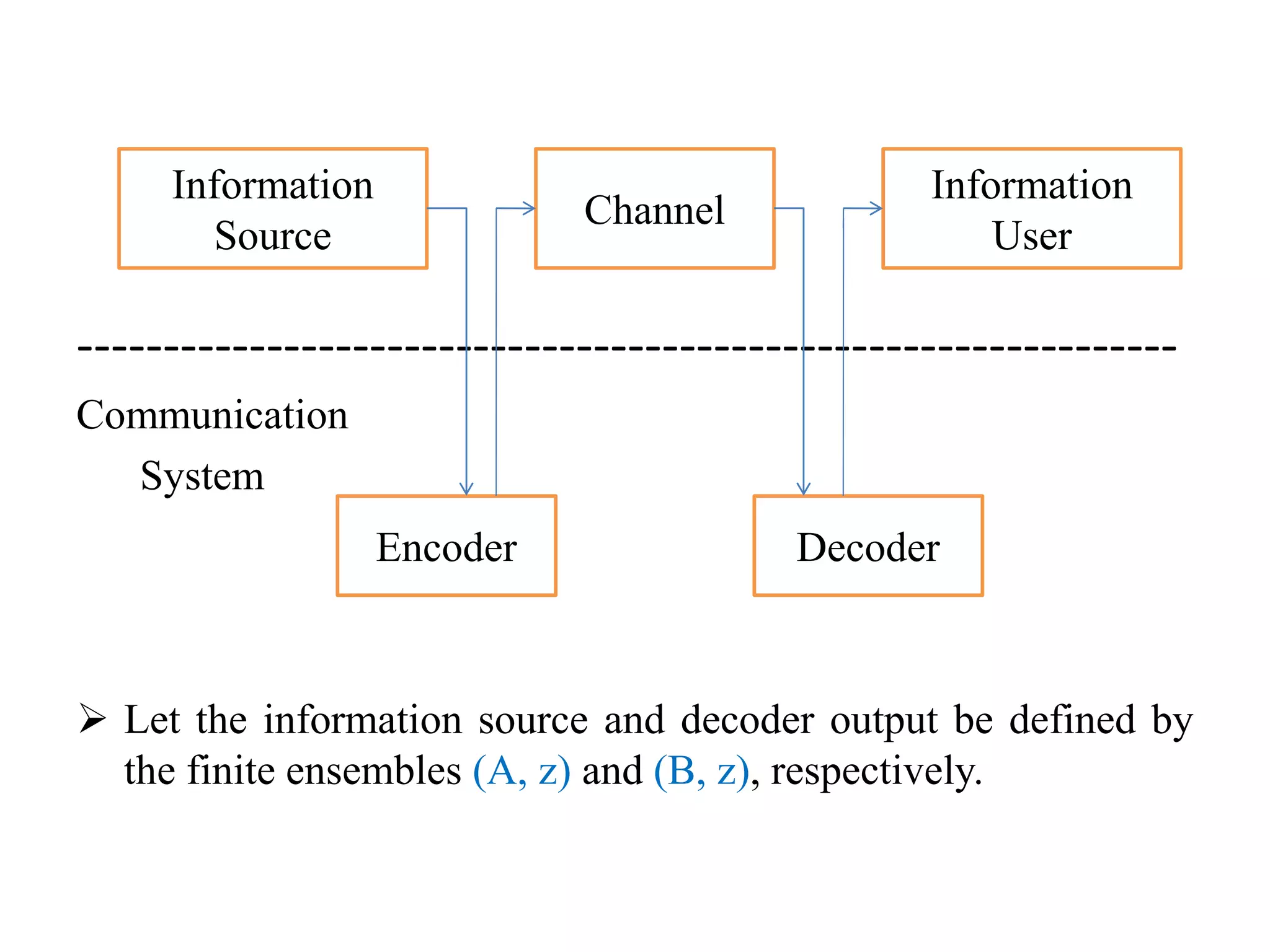
The document discusses the source coding theorem, which establishes fundamental limits on lossy communication over error-free channels where the goal is information compression. It addresses how to determine the smallest rate needed to convey information about a source to a user while constraining the average error introduced by compression to a maximum level D. This problem is studied by rate distortion theory, which models the encoding-decoding process as a deterministic channel and defines a distortion measure for the penalty between source and decoded outputs. The rate distortion function gives the minimum mutual information needed to satisfy a given distortion level D.





![The output of the source is random, so the
distoration also is a random variable whose
average value denoted d(Q), is
The notation d(Q) emphasizes that the average
distoration is a function of the encoding-
decoding procedure.
𝑄 𝐷={𝑞 𝑘𝑗|d(Q)≤D}
Rate distoration finction will be
R(D)= min
𝑄=𝑄𝑑
[𝐼(𝑧, 𝑣]
If D=0, then R(D) ≤ H(z).](https://image.slidesharecdn.com/sourcecodingtheorem-160820133812/75/Source-coding-theorem-7-2048.jpg)

