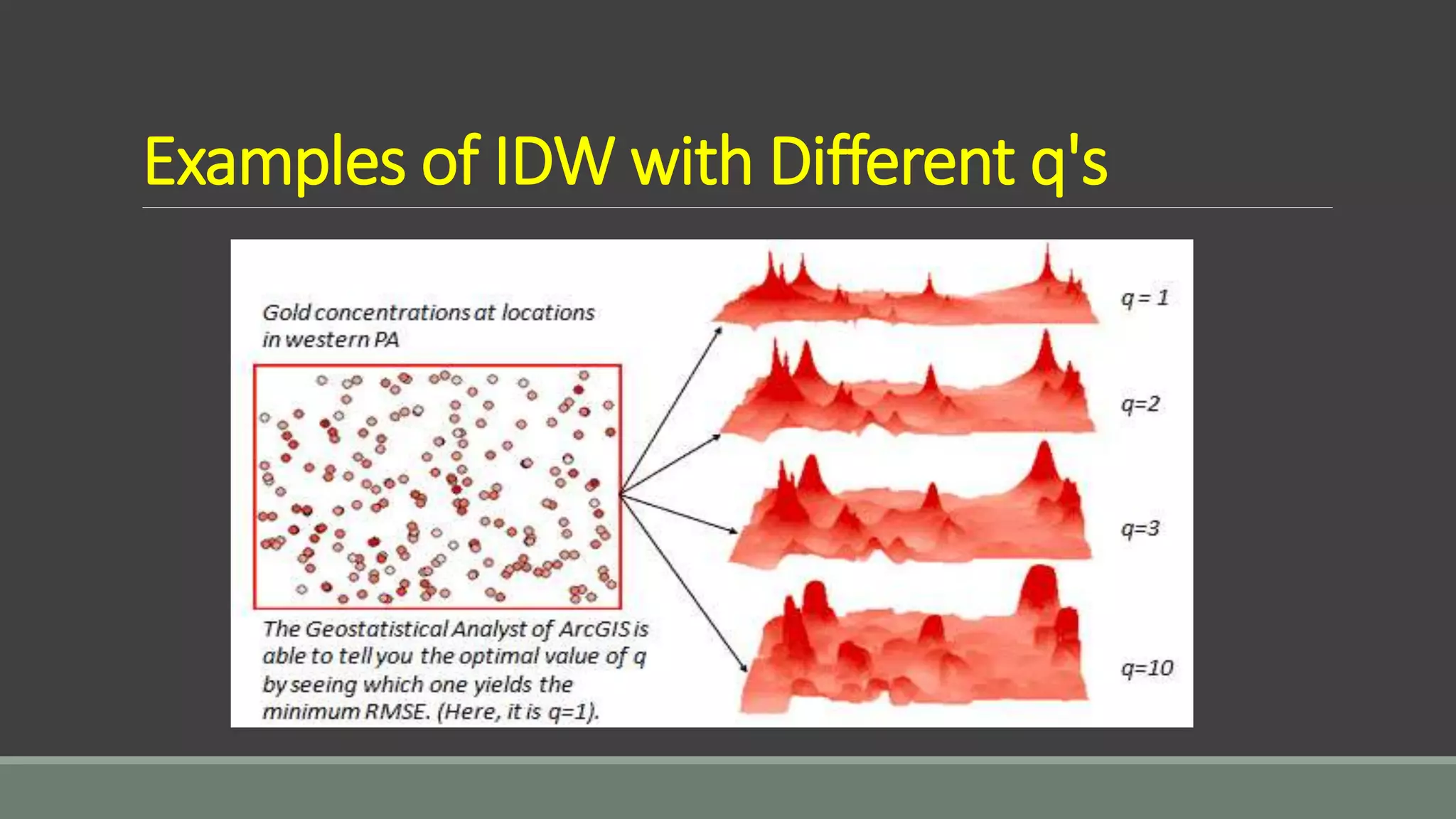
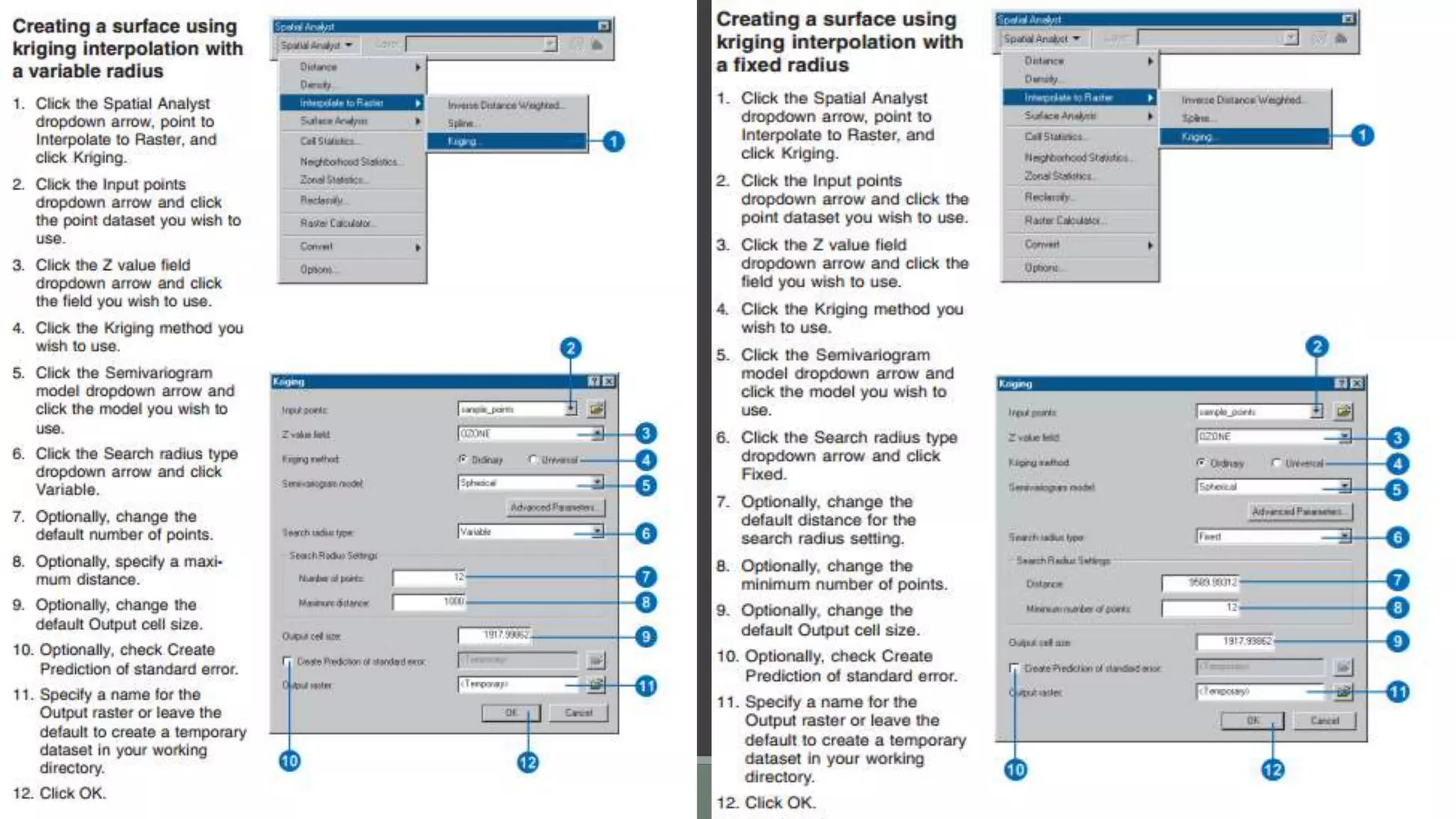
The document discusses spatial analysis, which examines the locations and relationships of geographic features, utilizing tools such as GIS for data manipulation and analysis. Key concepts include spatial data formats and interpolation methods, specifically focusing on inverse distance weighting (IDW) and kriging as techniques for predicting values at unknown locations based on surrounding data. The conclusion emphasizes the unique capabilities of GIS in handling spatial data and the importance of understanding data variation and correlation in spatial analysis.