Download to read offline
![ALGORITHM OF INSERTION IN STACK: (PUSH)
1. Insertion(a,top,item,max)
2. If top=max then
3. print âSTACK OVERFLOWâ
4. exit else
5. top=top+1 end if
6. a[top]=item
7. Exit](https://image.slidesharecdn.com/stackoperationalgorithmswithexample-210614134113/85/Stack-operation-algorithms-with-example-5-320.jpg)
![ALGORITHM OF DELETION IN STACK: (POP)
1. Deletion(a,top,item)
2. If top=0 then
3. print âSTACK UNDERFLOWâ
4. exit else
5. item=a[top] end if
6. top=top-1
7. Exit](https://image.slidesharecdn.com/stackoperationalgorithmswithexample-210614134113/85/Stack-operation-algorithms-with-example-6-320.jpg)
![ALGORITHM OF DISPLAY IN STACK:
⢠1. Display(top,i,a[i]) 2.If top=0 then
⢠2. Print âSTACK EMPTYâ
⢠Exit Else
⢠3. For i=top to 0
⢠Print a[i] End for
⢠4. exit](https://image.slidesharecdn.com/stackoperationalgorithmswithexample-210614134113/85/Stack-operation-algorithms-with-example-7-320.jpg)
![ALGORITHM OF INSERTION IN STACK: (PUSH)
1. Insertion(a,top,item,max)
2. If top=max then
3. print âSTACK OVERFLOWâ
4. exit else
5. top=top+1 end if
6. a[top]=item
7. Exit](https://image.slidesharecdn.com/stackoperationalgorithmswithexample-210614134113/75/Stack-operation-algorithms-with-example-5-2048.jpg)
![ALGORITHM OF DELETION IN STACK: (POP)
1. Deletion(a,top,item)
2. If top=0 then
3. print âSTACK UNDERFLOWâ
4. exit else
5. item=a[top] end if
6. top=top-1
7. Exit](https://image.slidesharecdn.com/stackoperationalgorithmswithexample-210614134113/75/Stack-operation-algorithms-with-example-6-2048.jpg)
![ALGORITHM OF DISPLAY IN STACK:
⢠1. Display(top,i,a[i]) 2.If top=0 then
⢠2. Print âSTACK EMPTYâ
⢠Exit Else
⢠3. For i=top to 0
⢠Print a[i] End for
⢠4. exit](https://image.slidesharecdn.com/stackoperationalgorithmswithexample-210614134113/75/Stack-operation-algorithms-with-example-7-2048.jpg)
Uploaded byNamanKikani
Stack operation algorithms with example
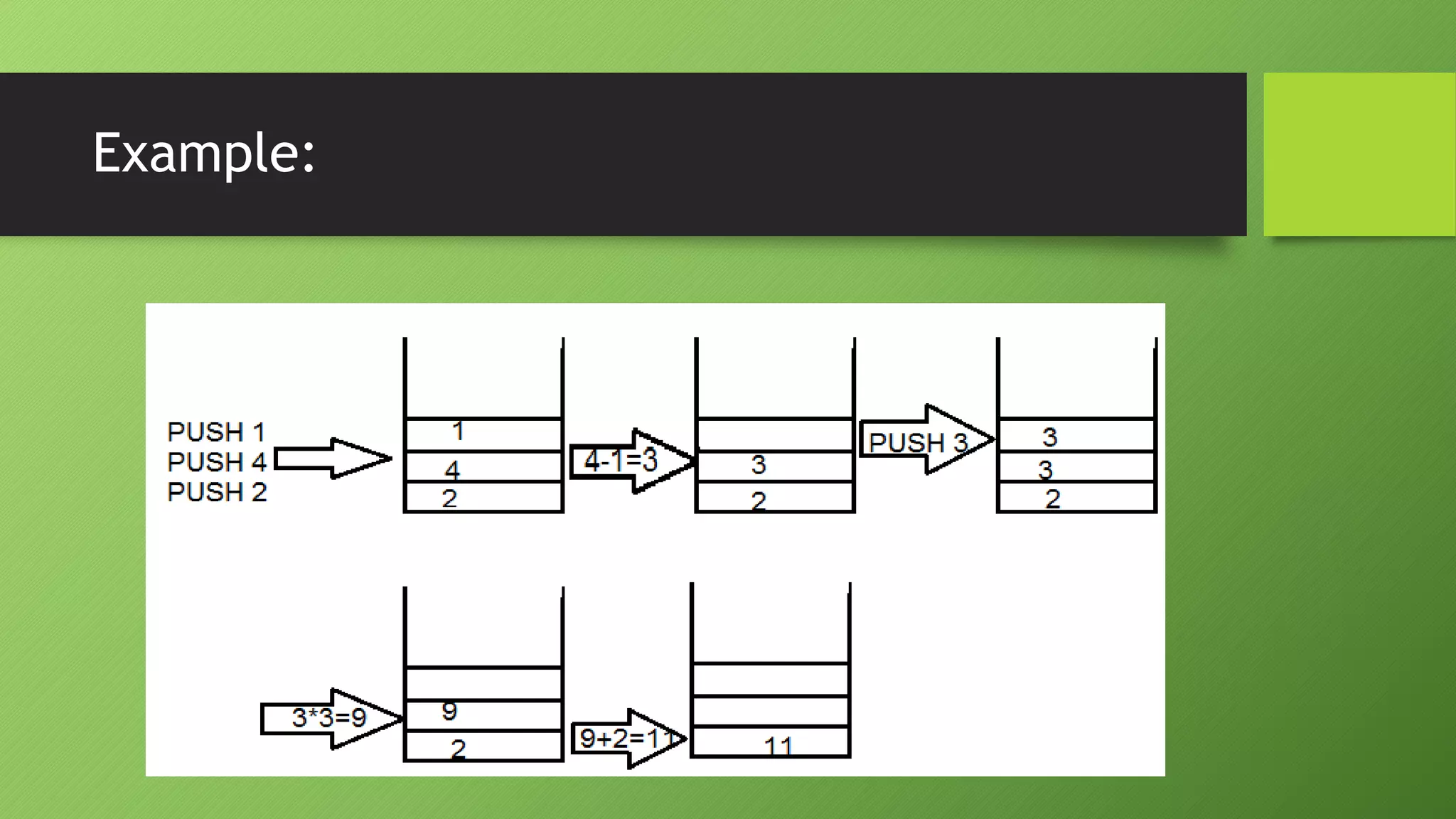
This document discusses stacks and algorithms for common stack operations. It defines a stack as a last-in, first-out data structure where the last item added is the first removed. The key operations are PUSH to insert an item and POP to remove an item from the top. Algorithms are provided for PUSH, POP, and displaying the stack. As an example, the document shows the steps to convert an infix notation expression to postfix.
EducationâŚ
More Related Content
![Data Structures - Lecture 9 [Stack & Queue using Linked List]](https://cdn.slidesharecdn.com/ss_thumbnails/lecture-9stackqueueusinglinkedlist-150219032411-conversion-gate02-thumbnail.jpg?width=600ounds&width=560&fit=bounds)
![Data Structures - Lecture 8 [Sorting Algorithms]](https://cdn.slidesharecdn.com/ss_thumbnails/lecture-8sortingalgorithms-150205105023-conversion-gate02-thumbnail.jpg?width=600ounds&width=560&fit=bounds)
Similar to Stack operation algorithms with example
Stack operation algorithms with example
- 1. Stack operation algorithms withexample KIKANI NAMAN BHARATBHAI 20SS02IT027 DATA STRUCTURES
- 2. What is Stack? â˘A stack is called a last-in-first-out (LIFO) collection. This means that the last thing we added (pushed) is the first thing that gets pulled (popped) off. ⢠A stack is a sequence of items that are accessible at only one end of the sequence.
- 3. Operations that canbe performed on STACK: ď PUSH. ď POP.
- 4. Procedure/Methodology PUSH : Itis used to insert items into the stack. POP: It is used to delete items from stack. TOP: It represents the current location of data in stack.
- 5. ALGORITHM OF INSERTIONIN STACK: (PUSH) 1. Insertion(a,top,item,max) 2. If top=max then 3. print âSTACK OVERFLOWâ 4. exit else 5. top=top+1 end if 6. a[top]=item 7. Exit
- 6. ALGORITHM OF DELETIONIN STACK: (POP) 1. Deletion(a,top,item) 2. If top=0 then 3. print âSTACK UNDERFLOWâ 4. exit else 5. item=a[top] end if 6. top=top-1 7. Exit
- 7. ALGORITHM OF DISPLAYIN STACK: ⢠1. Display(top,i,a[i]) 2.If top=0 then ⢠2. Print âSTACK EMPTYâ ⢠Exit Else ⢠3. For i=top to 0 ⢠Print a[i] End for ⢠4. exit
- 8. Conversion of INFIXto POSTFIX conversion: ⢠Example: 2+(4-1)*3 step1 ⢠2+41-*3 step2 ⢠2+41-3* step3 ⢠241-3*+ step4
- 9.
- 10.
Editor's Notes
- #2Â 1