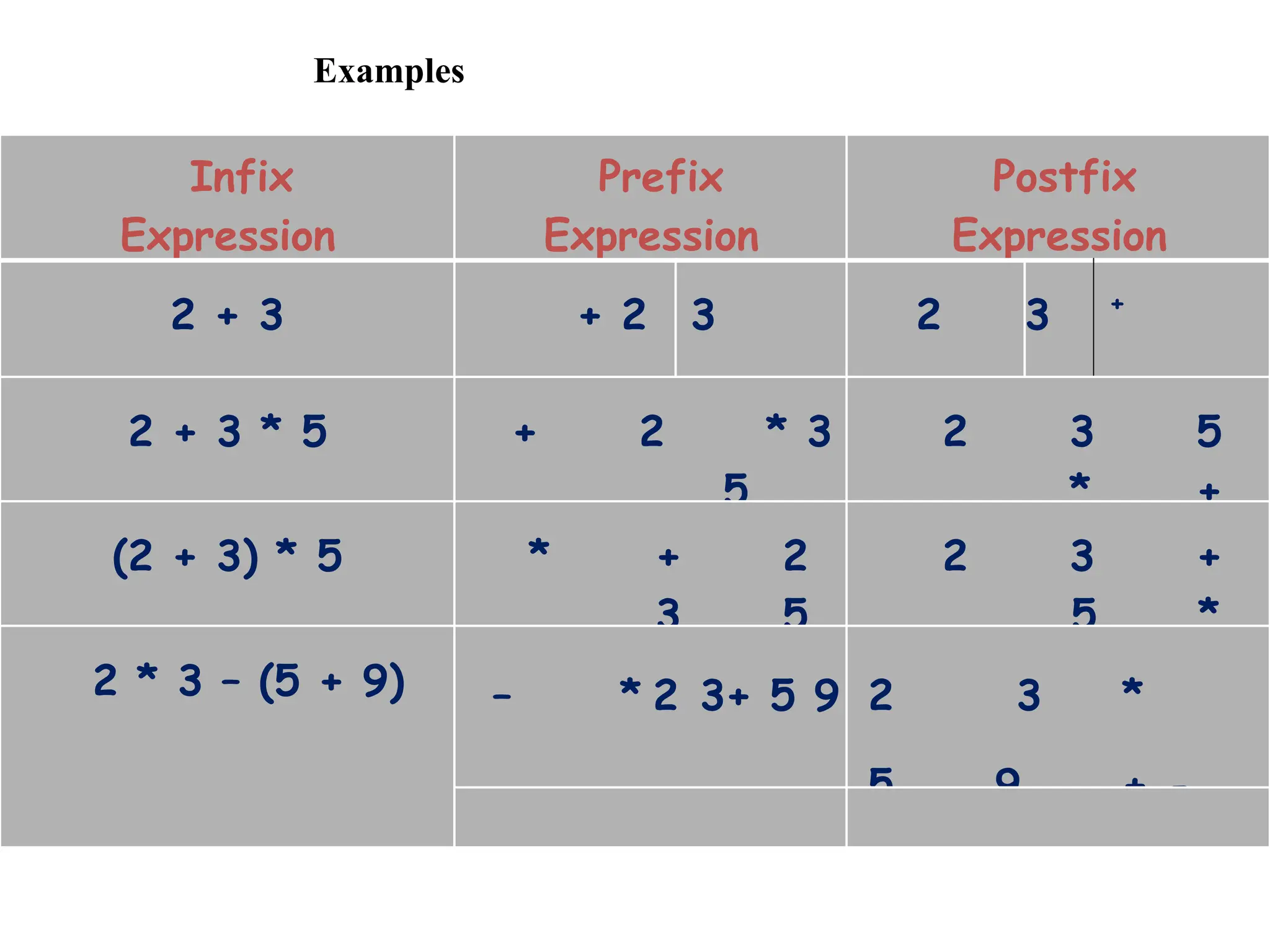
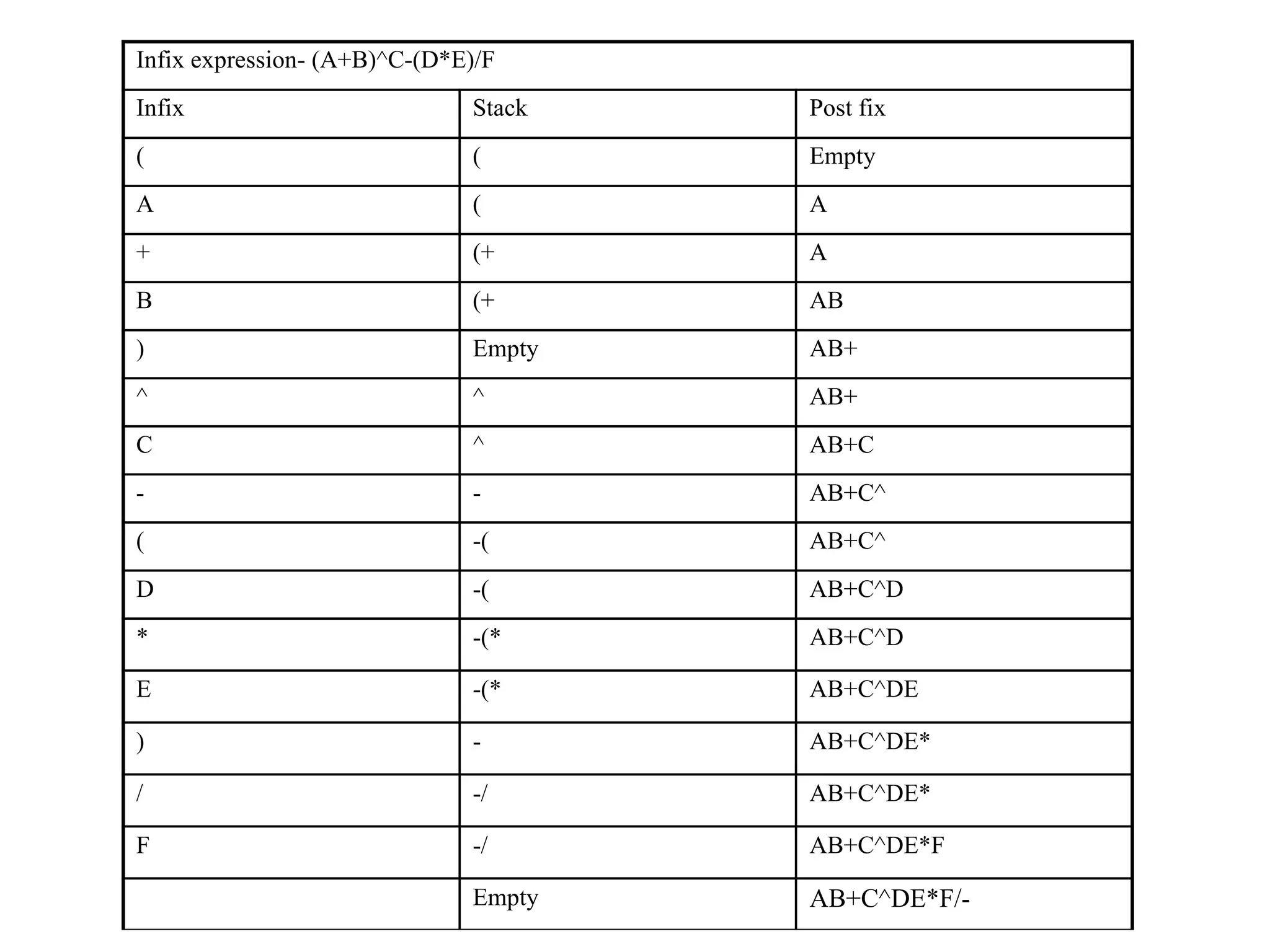
The document provides an overview of stacks and queues, including their definitions, operations, and implementations using arrays and linked lists. It discusses key concepts such as last in first out (LIFO) for stacks and various applications like expression evaluation and parenthesis matching. Additionally, it covers algorithms for converting infix expressions to postfix and prefix notations, along with the evaluation of postfix expressions.

![Module 2 : Stack and Queues
Refer Module 2 of Syllabus [CSC303 (SE AI&DS/ SE Comps)]
2.1 Introduction, ADT of Stack, Operations on Stack, Array
Implementation of
Stack, Applications of Stack-Well form-ness of Parenthesis, Infix
to Postfix Conversion and Postfix Evaluation, Recursion.
2.2 Introduction, ADT of Queue, Operations on Queue, Array
Implementation of Queue, Types of Queue-Circular Queue,
Priority Queue, Introduction of Double
Ended Queue, Applications of Queue.](https://image.slidesharecdn.com/stacks-240819101922-2c31c326/75/Stacks-and-queues-using-aaray-line-pptx-2-2048.jpg)



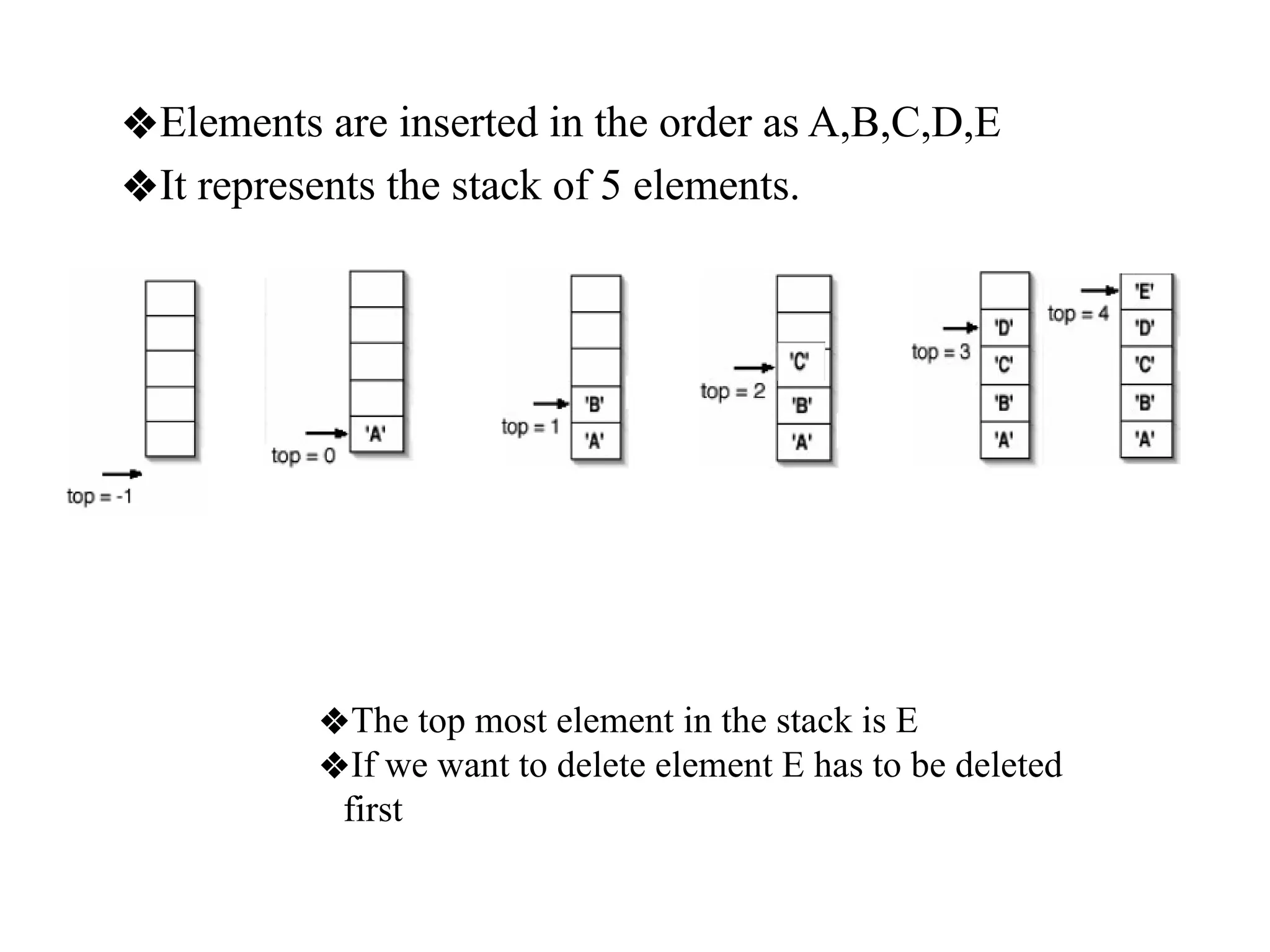
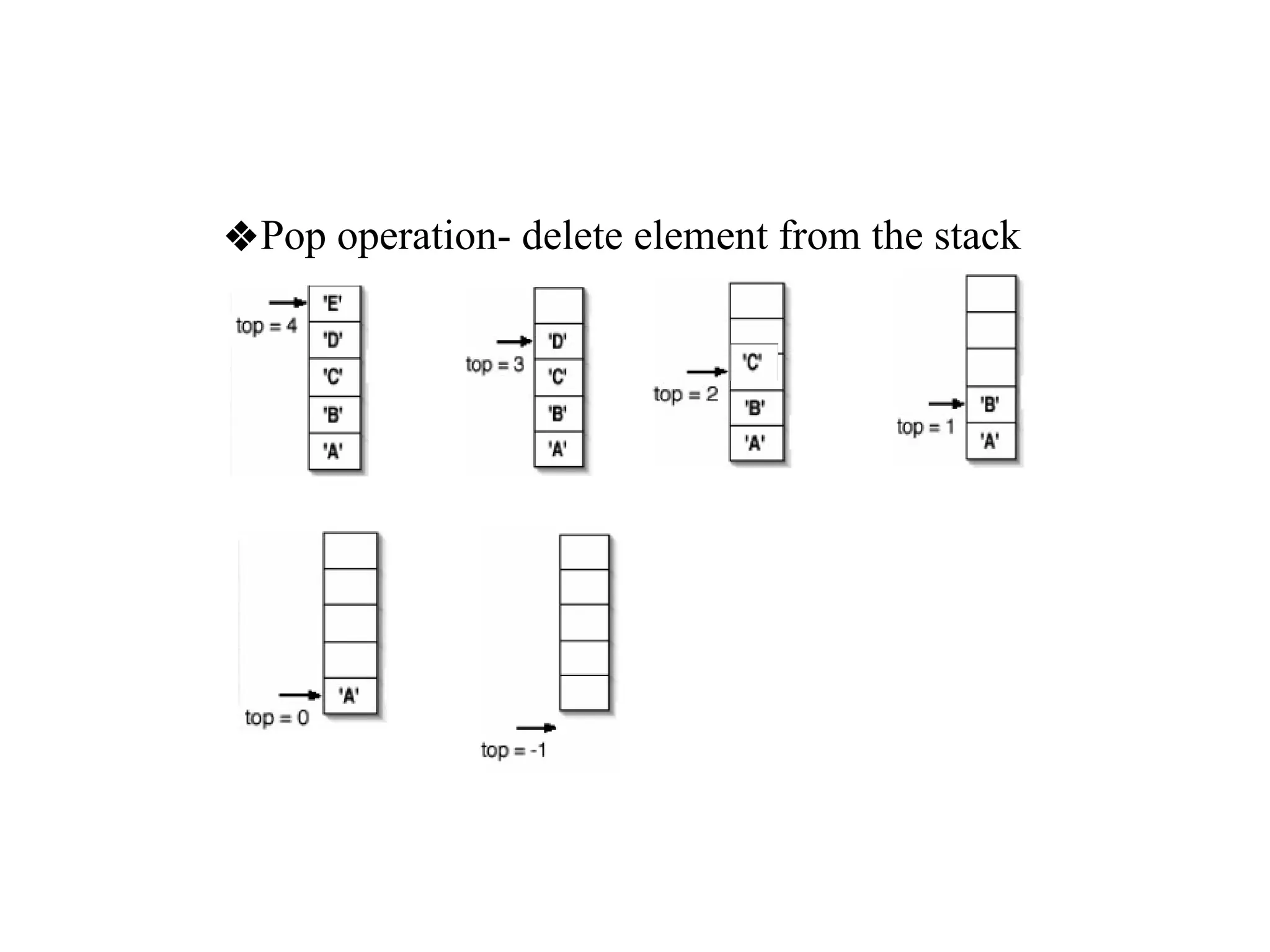
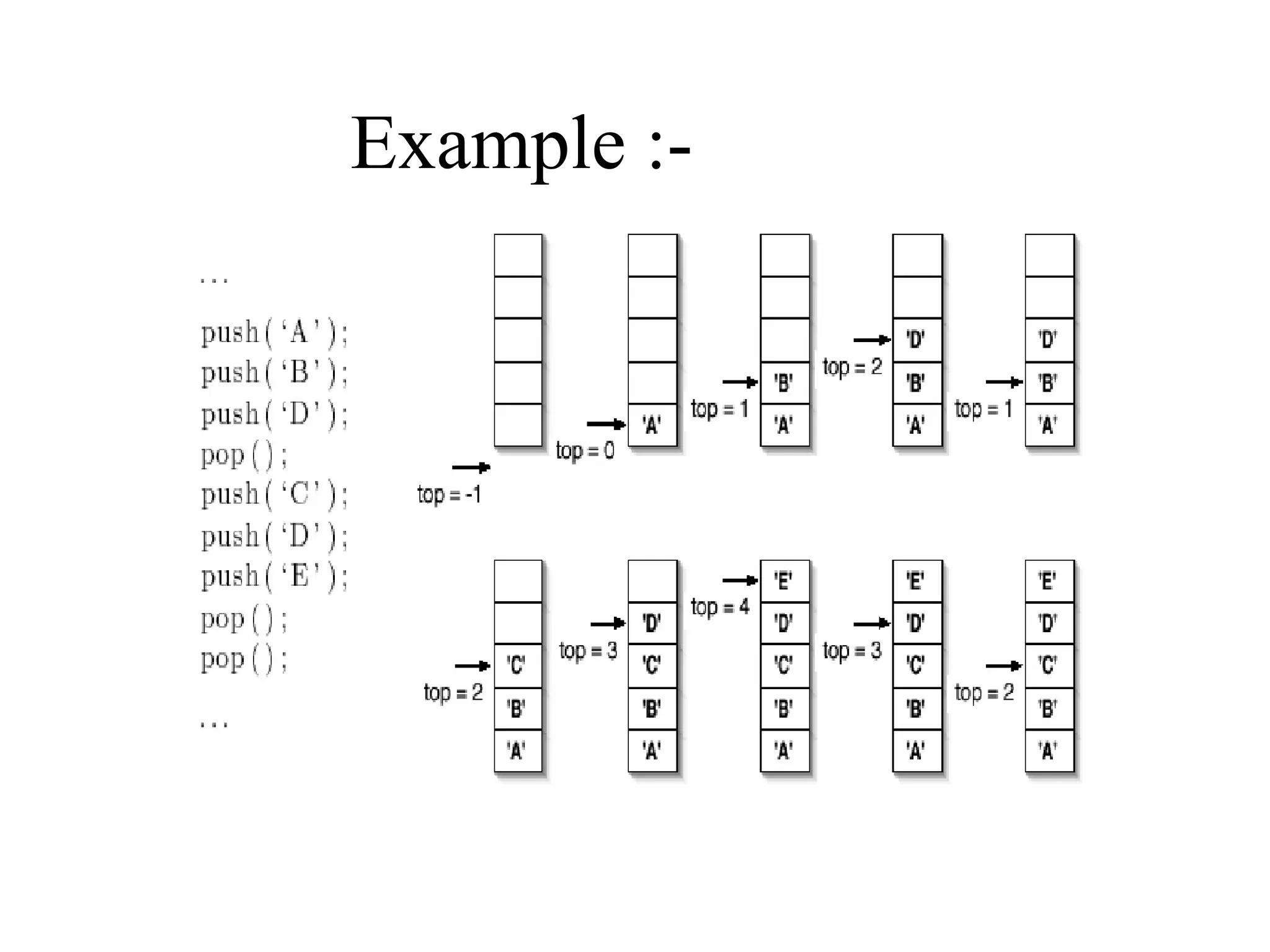
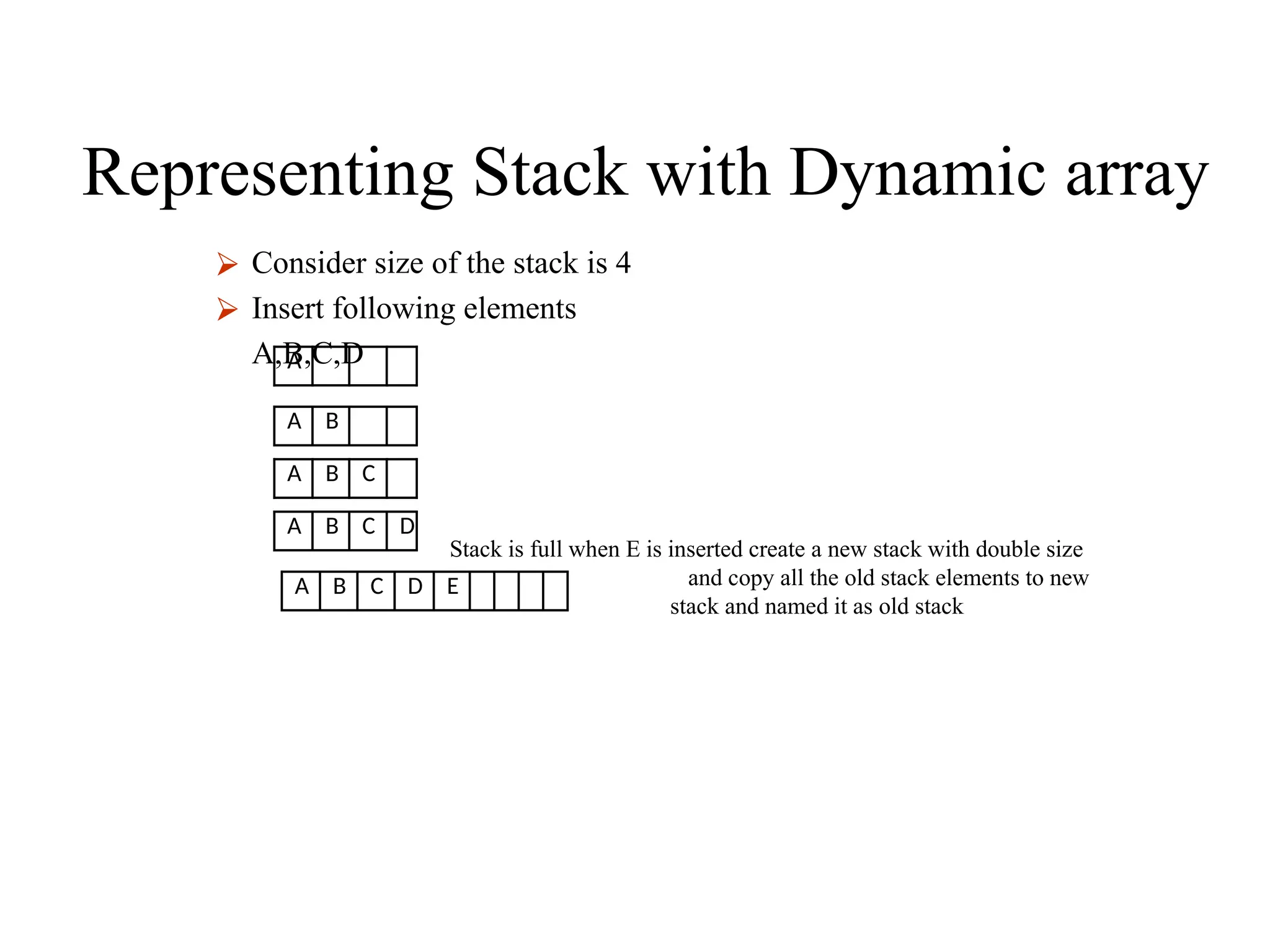
![Implementing stack using arrays
Algorithm for creating empty stack:
Step 1 - Include all the header files which are used in the program and define a
constant 'SIZE' with specific value.
Step 2 - Declare all the functions used in stack implementation.
Step 3 - Create a one dimensional array with fixed size (int stack[SIZE])
Step 4 - Define a integer variable 'top' and initialize with '-1'. (int top = -1)
Step 5 - In main method, display menu with list of operations and make
suitable function calls to perform operation selected by the user on the stack.](https://image.slidesharecdn.com/stacks-240819101922-2c31c326/75/Stacks-and-queues-using-aaray-line-pptx-9-2048.jpg)
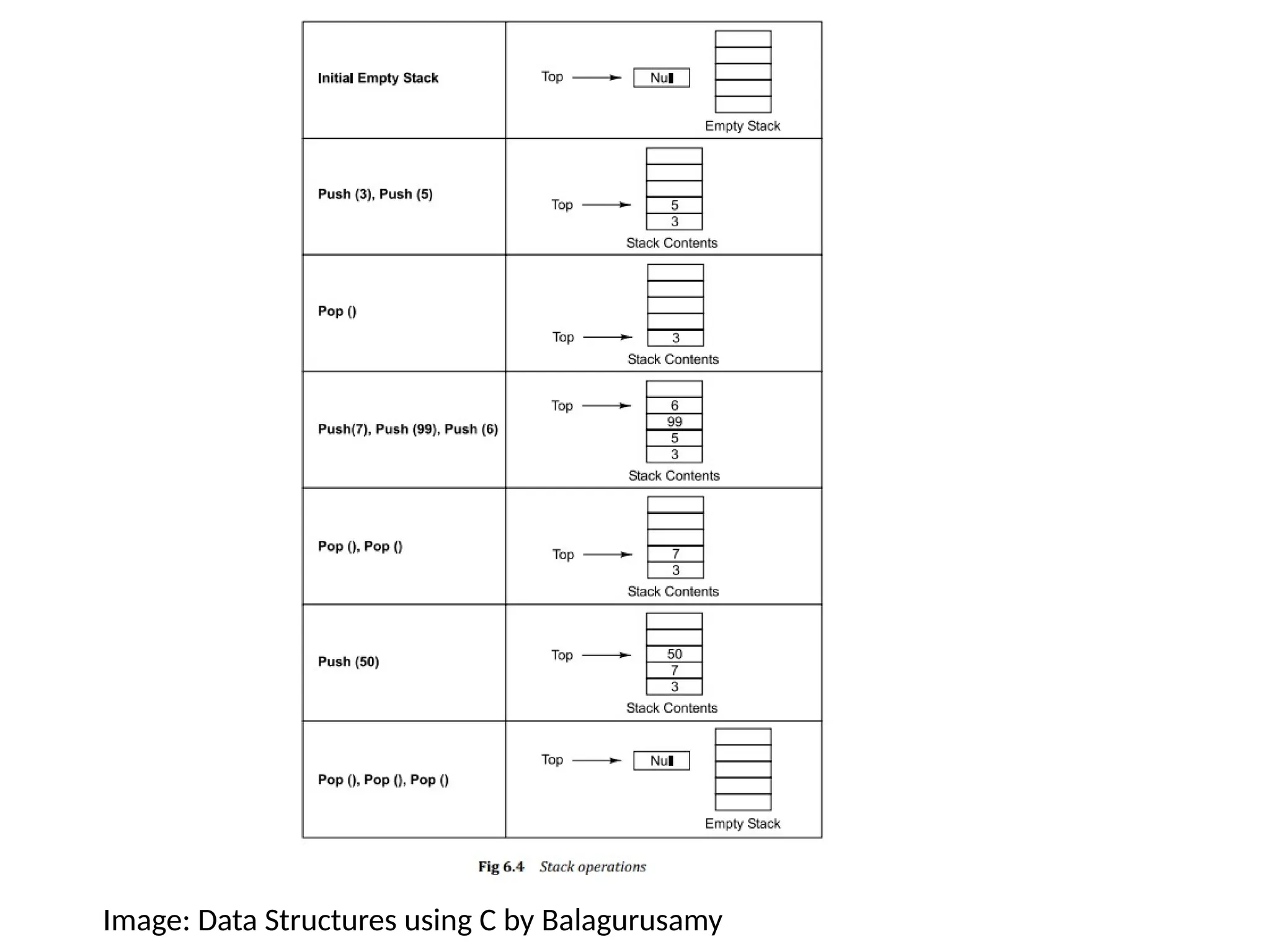
![Algorithm for inserting element into the stack:
push(value) - Inserting value into the stack
Step 1 - Check whether stack is FULL. (if top = SIZE-1)
Step 2 - If it is FULL, then display "Stack is FULL!!! Insertion is not possible!!!" and
terminate the function.
Step 3 - If it is NOT FULL, then increment top value by one (top top +1
🡨 ) and set
stack[top] to value (stack[top] value
🡨 ).](https://image.slidesharecdn.com/stacks-240819101922-2c31c326/75/Stacks-and-queues-using-aaray-line-pptx-10-2048.jpg)

![Algorithm to delete elements from the stack:
pop() - Delete a value from the Stack
Step 1 - Check whether stack is EMPTY. (if top = -1)
Step 2 - If it is EMPTY, then display "Stack is EMPTY!!! Deletion is not
possible!!!" and terminate the function.
Step 3 - If it is NOT EMPTY, then delete stack[top] and decrement top value by
one (top top -1
🡨 ).](https://image.slidesharecdn.com/stacks-240819101922-2c31c326/75/Stacks-and-queues-using-aaray-line-pptx-12-2048.jpg)

![display() - Displays the elements of a Stack
We can use the following steps to display the elements of a stack
Step 1 - Check whether stack is EMPTY. (if top = -1)
Step 2 - If it is EMPTY, then display "Stack is EMPTY!!!" and terminate the
function.
Step 3 - If it is NOT EMPTY, then define a variable 'i' and initialize with top.
Display stack[i] value and decrement i value by one (i--).
Step 3 - Repeat above step until i value becomes '0'.](https://image.slidesharecdn.com/stacks-240819101922-2c31c326/75/Stacks-and-queues-using-aaray-line-pptx-14-2048.jpg)