1. The document discusses stacks and queues as linear data structures. It describes stack operations like push and pop and provides algorithms for implementing these operations.
2. An example program for implementing a stack using an array is presented, with functions defined for push, pop, and display operations on the stack.
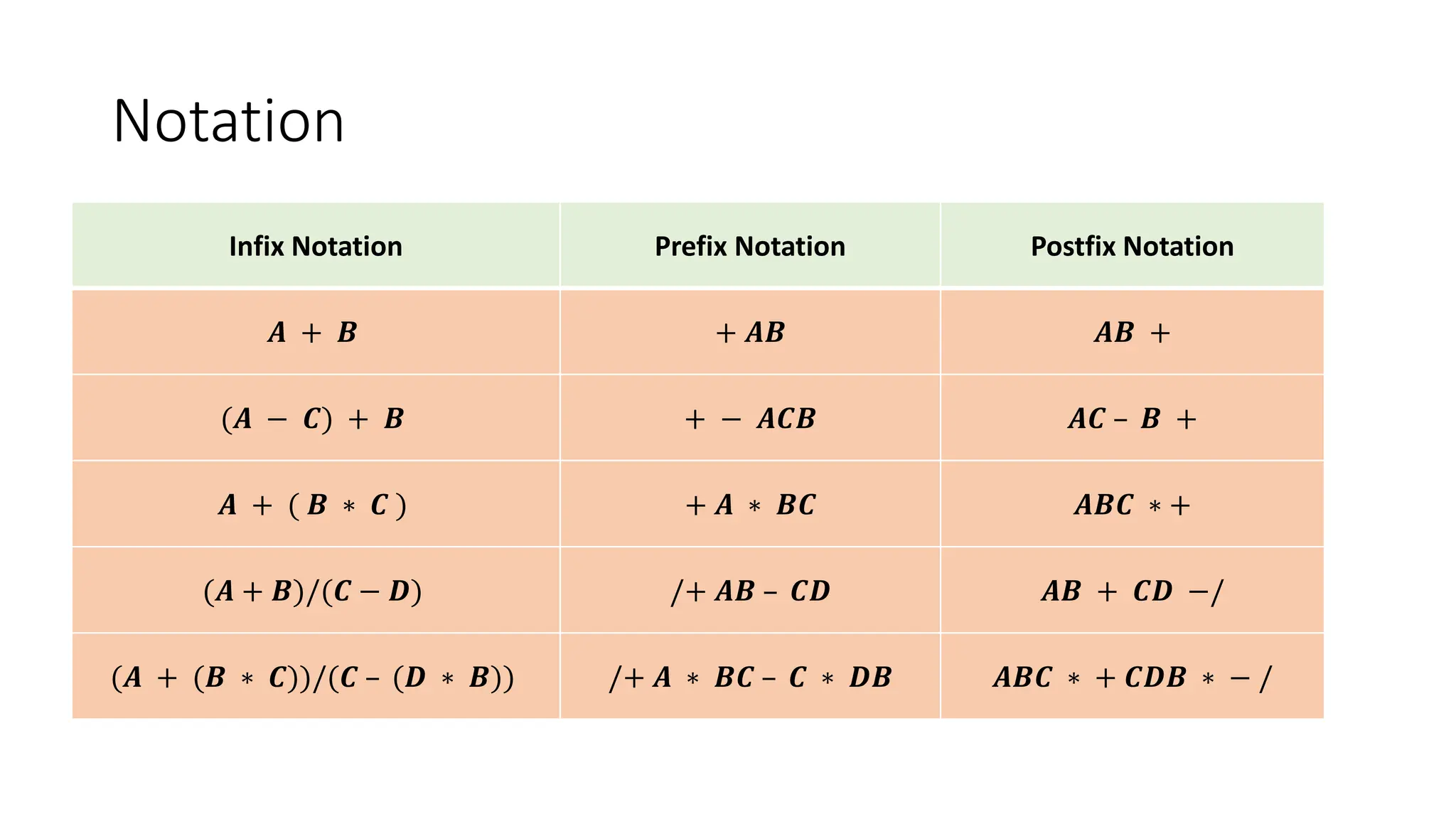
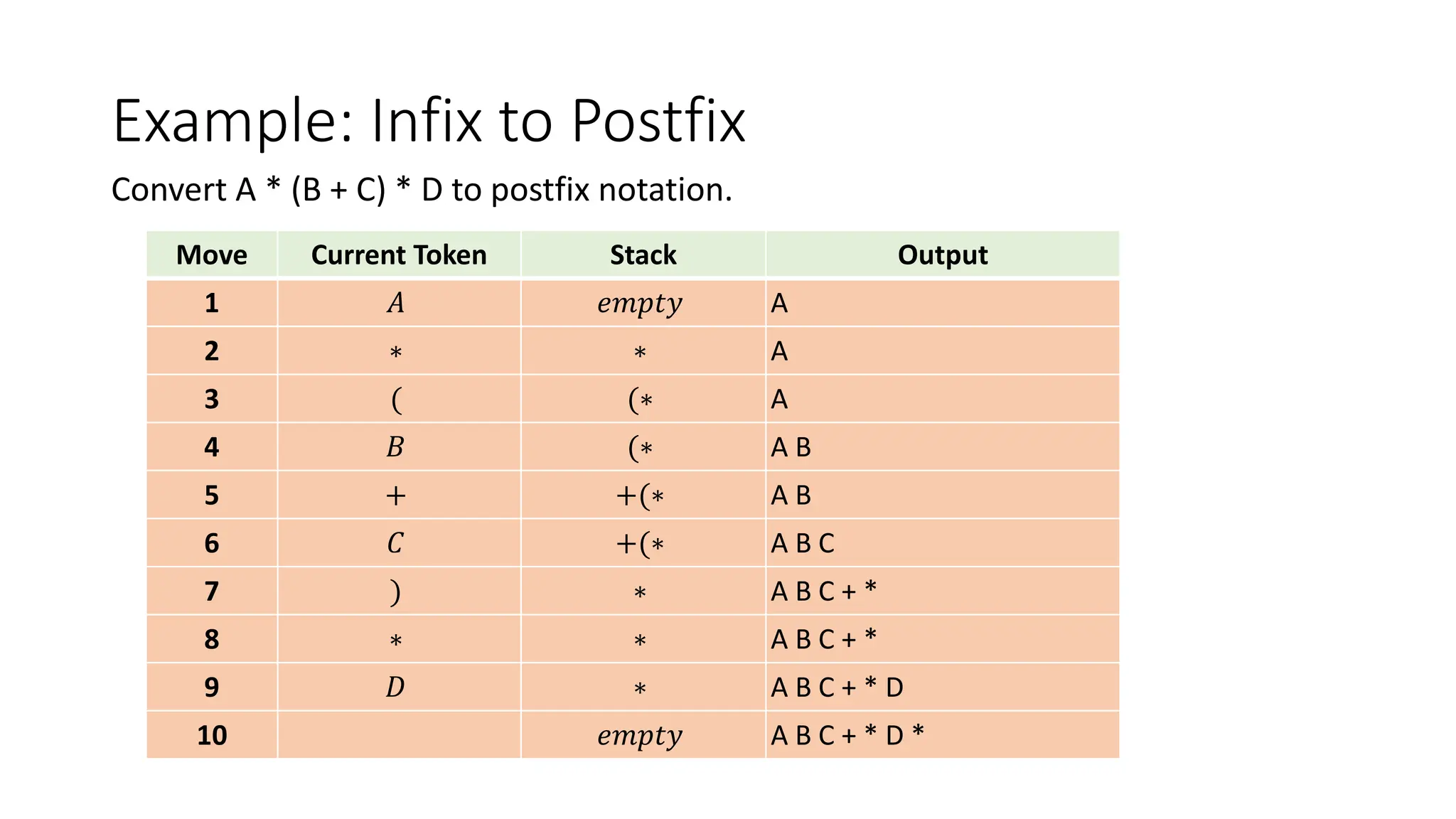
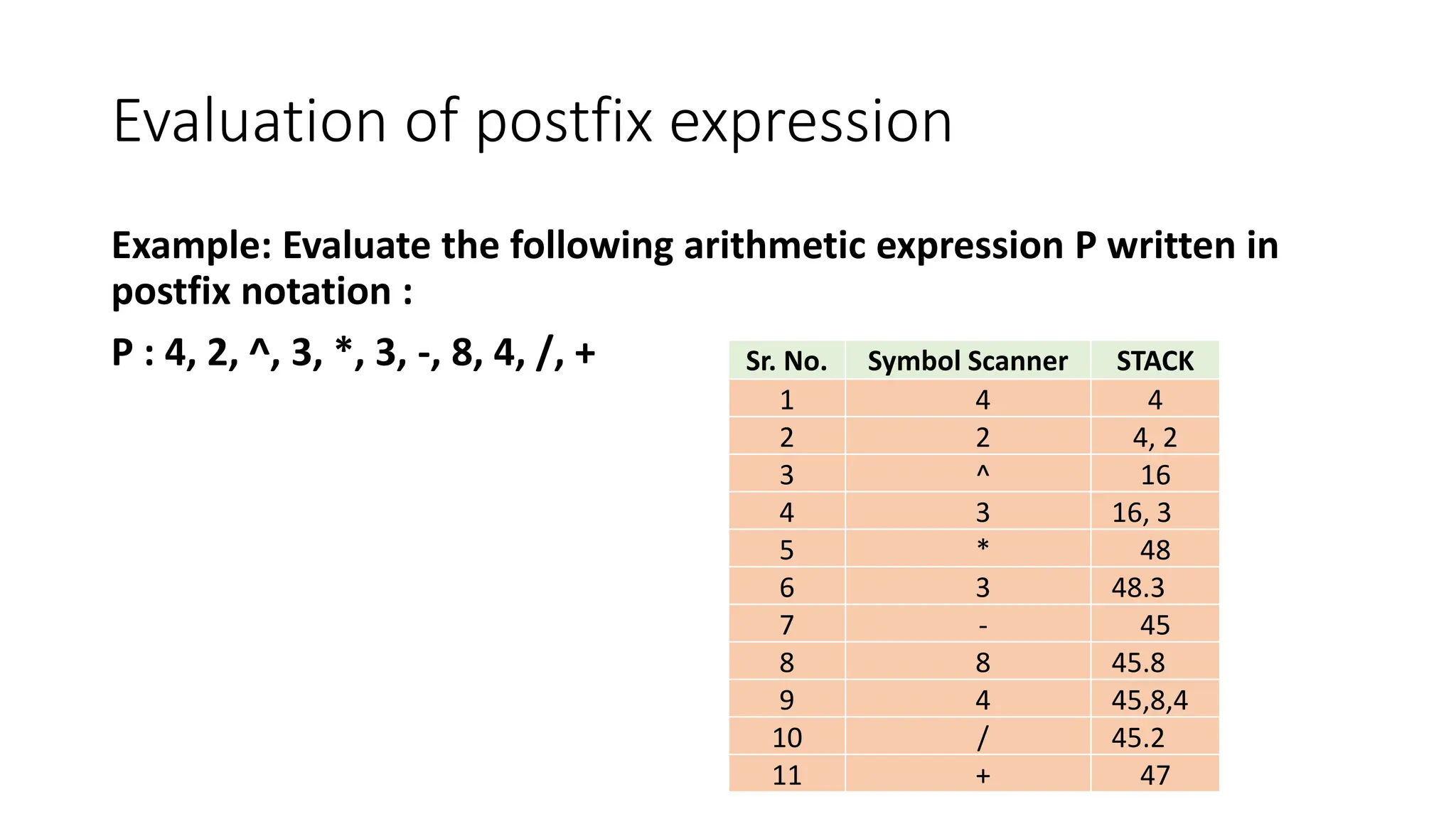
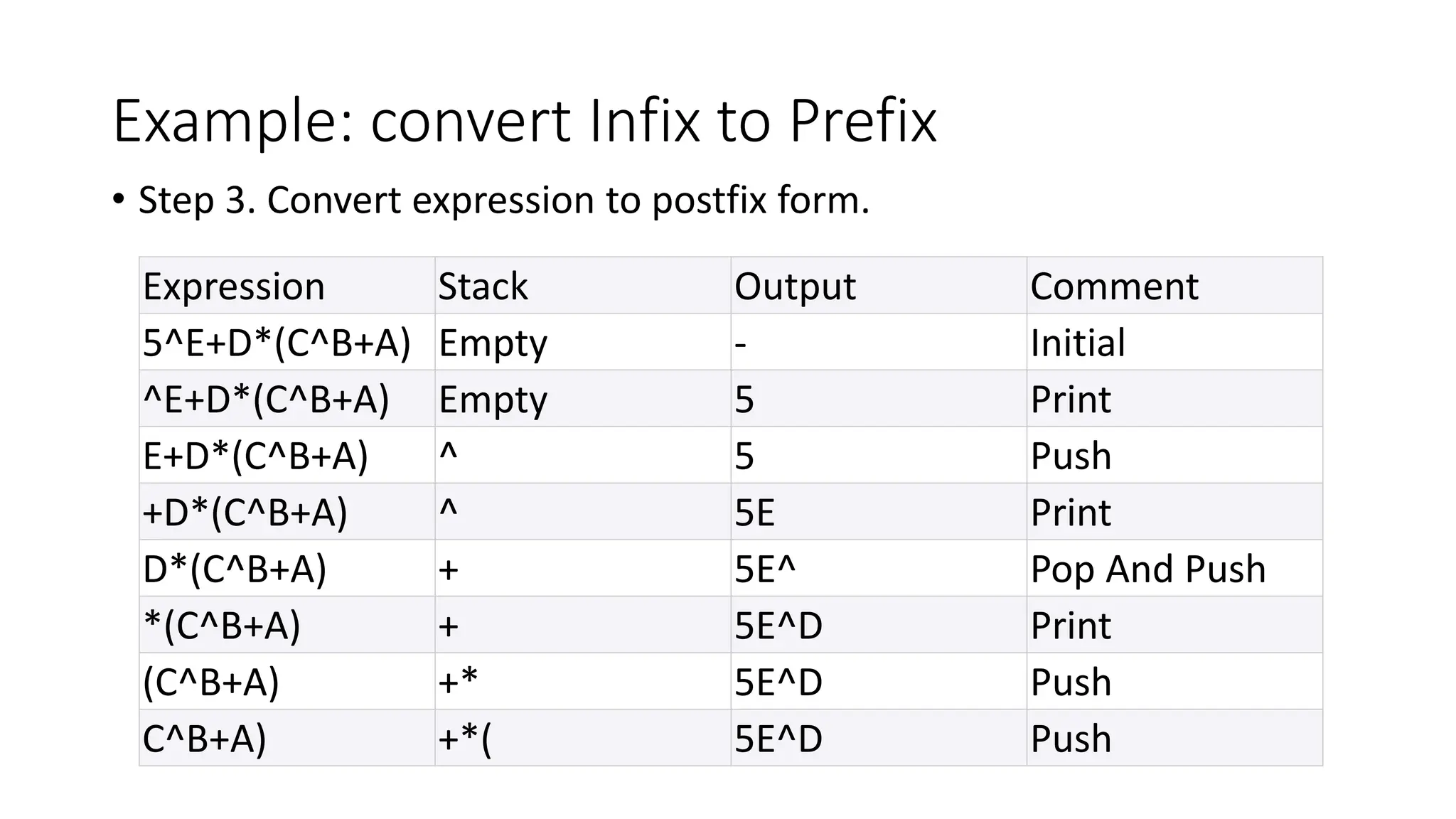
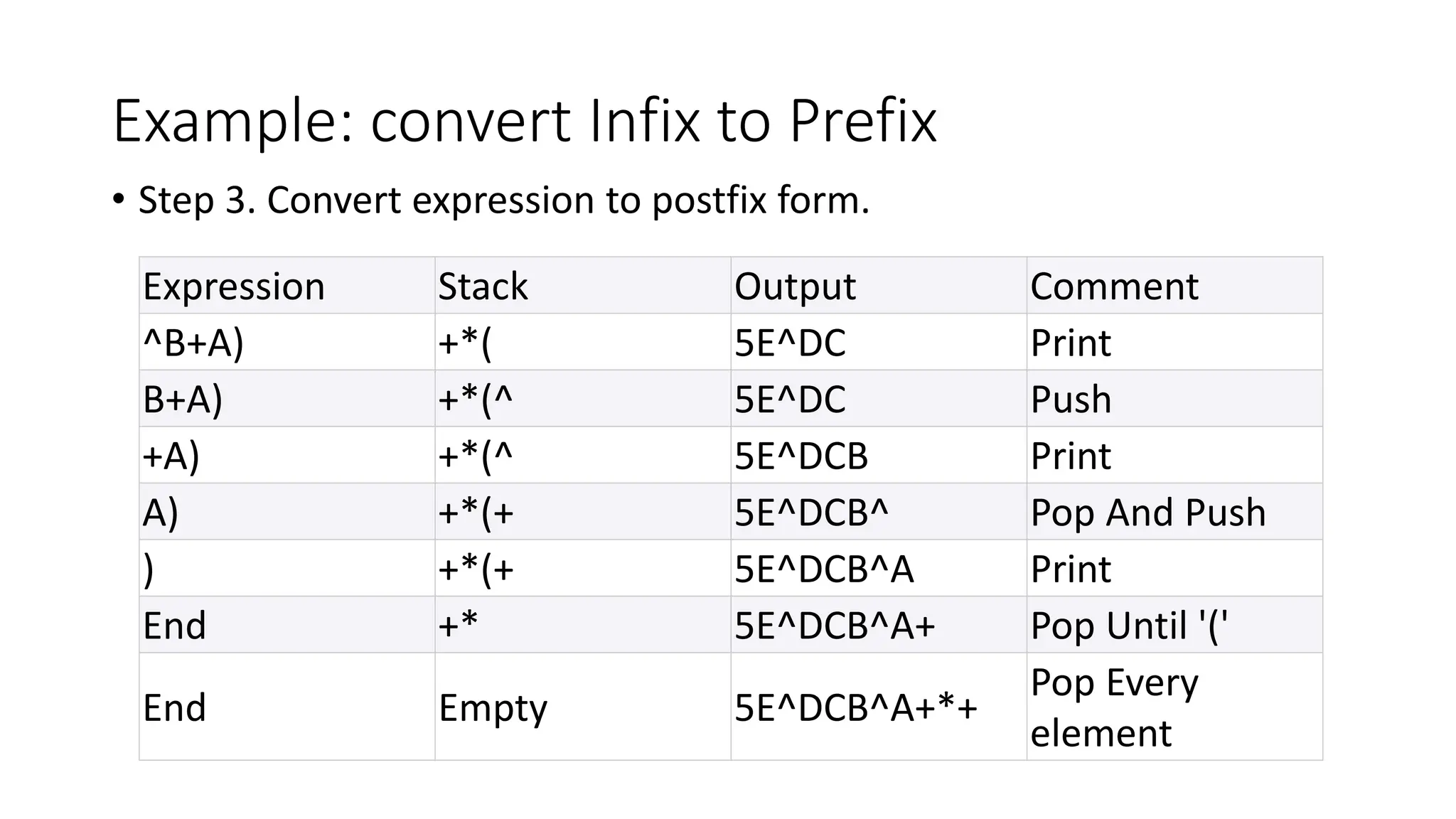
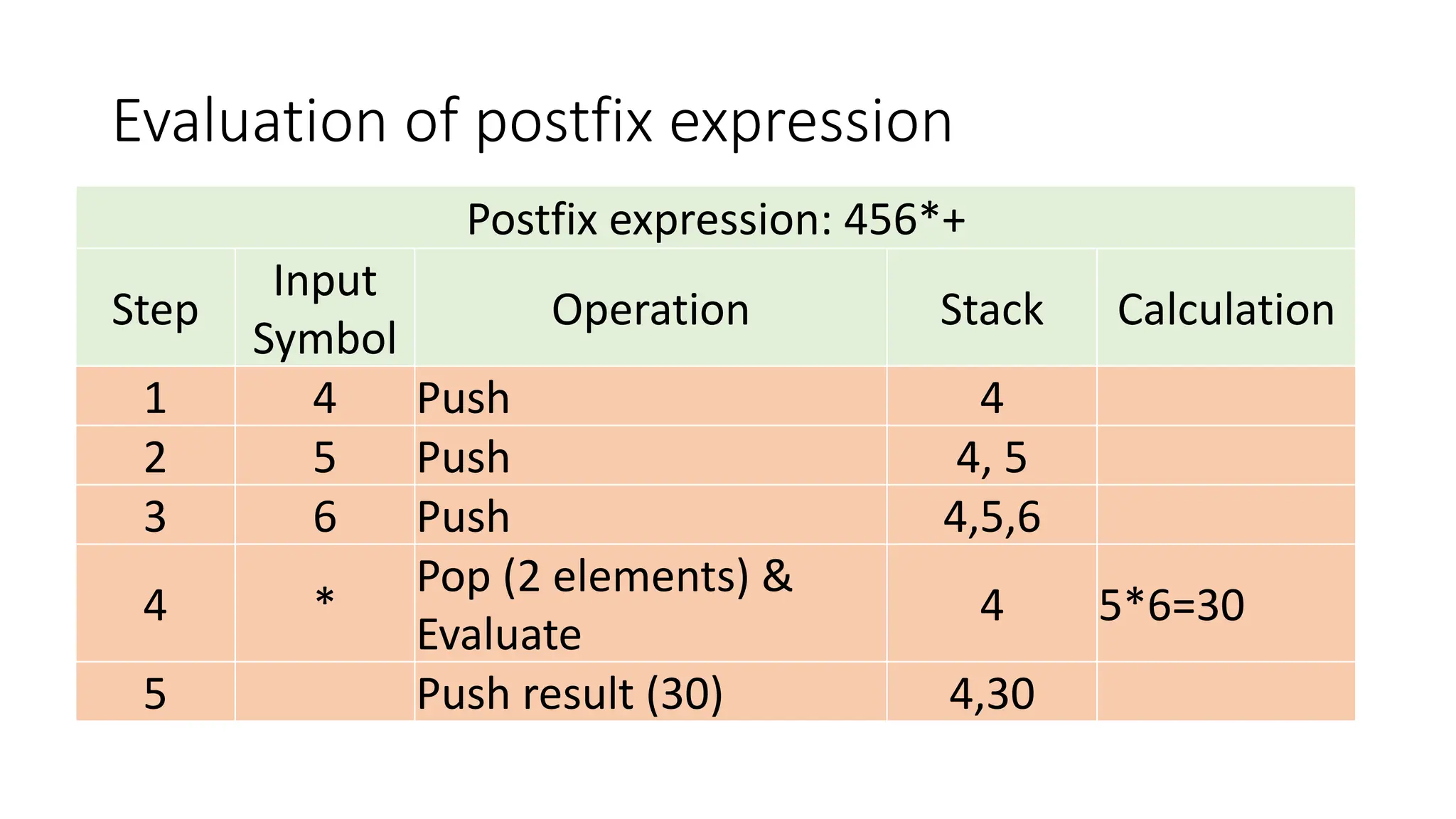
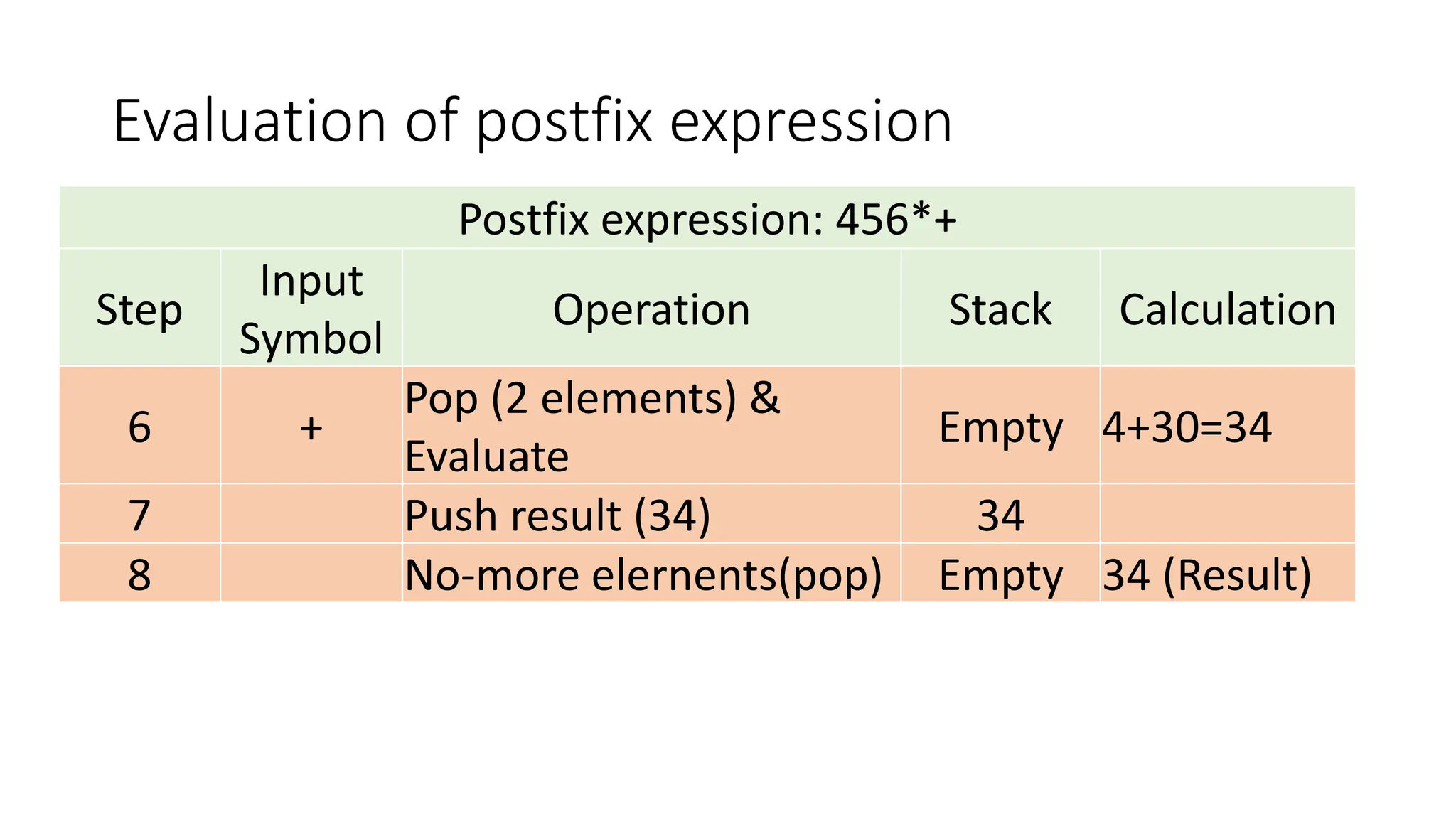
3. Applications of stacks discussed include reversing a list or string by pushing characters onto a stack and popping them off in reverse order, and converting infix expressions to postfix using a stack.













![Program Implementation of Stack Using Array
#𝒊𝒏𝒄𝒍𝒖𝒅𝒆 < 𝒔𝒕𝒅𝒊𝒐. 𝒉 >
#𝒊𝒏𝒄𝒍𝒖𝒅𝒆 < 𝒄𝒐𝒏𝒊𝒐. 𝒉 >
𝒊𝒏𝒕 𝒔𝒕𝒂𝒄𝒌[𝟏𝟎𝟎], 𝒄𝒉𝒐𝒊𝒄𝒆, 𝒏, 𝒕𝒐𝒑, 𝒙, 𝒊;
𝒗𝒐𝒊𝒅 𝒑𝒖𝒔𝒉(𝒗𝒐𝒊𝒅);
𝒗𝒐𝒊𝒅 𝒑𝒐𝒑(𝒗𝒐𝒊𝒅);
𝒗𝒐𝒊𝒅 𝒅𝒊𝒔𝒑𝒍𝒂𝒚(𝒗𝒐𝒊𝒅);
𝒊𝒏𝒕 𝒎𝒂𝒊𝒏()
{
𝒄𝒍𝒓𝒔𝒄𝒓();
𝒕𝒐𝒑 = −𝟏;
𝒑𝒓𝒊𝒏𝒕𝒇("𝒏 𝑬𝒏𝒕𝒆𝒓 𝒕𝒉𝒆 𝒔𝒊𝒛𝒆 𝒐𝒇 𝑺𝑻𝑨𝑪𝑲[𝑴𝑨𝑿 = 𝟏𝟎𝟎]: ");
𝒔𝒄𝒂𝒏𝒇("%𝒅", &𝒏);
𝒑𝒓𝒊𝒏𝒕𝒇("𝒏𝒕 𝑺𝑻𝑨𝑪𝑲 𝑶𝑷𝑬𝑹𝑨𝑻𝑰𝑶𝑵𝑺 𝑼𝑺𝑰𝑵𝑮 𝑨𝑹𝑹𝑨𝒀");
𝒑𝒓𝒊𝒏𝒕𝒇("𝒏𝒕 −−−−−−−−−−−−−−−−−−−− −");
𝒑𝒓𝒊𝒏𝒕𝒇("𝒏𝒕 𝟏. 𝑷𝑼𝑺𝑯𝒏𝒕 𝟐. 𝑷𝑶𝑷𝒏𝒕 𝟑. 𝑫𝑰𝑺𝑷𝑳𝑨𝒀𝒏𝒕 𝟒. 𝑬𝑿𝑰𝑻");
𝒅𝒐
{
𝒑𝒓𝒊𝒏𝒕𝒇("𝒏 𝑬𝒏𝒕𝒆𝒓 𝒕𝒉𝒆 𝑪𝒉𝒐𝒊𝒄𝒆: ");
𝒔𝒄𝒂𝒏𝒇("%𝒅", &𝒄𝒉𝒐𝒊𝒄𝒆);](https://image.slidesharecdn.com/unit3stacksandqueues-240116110152-9d232533/75/Unit-3-Stacks-and-Queues-pptx-14-2048.jpg)


![Program Implementation of Stack Using Array
𝒗𝒐𝒊𝒅 𝒑𝒐𝒑()
{
𝒊𝒇(𝒕𝒐𝒑 <= −𝟏)
𝒑𝒓𝒊𝒏𝒕𝒇("𝒏𝒕 𝑺𝒕𝒂𝒄𝒌 𝒊𝒔 𝒖𝒏𝒅𝒆𝒓 𝒇𝒍𝒐𝒘");
𝒆𝒍𝒔𝒆
{
𝒑𝒓𝒊𝒏𝒕𝒇("𝒏𝒕 𝑻𝒉𝒆 𝒑𝒐𝒑𝒑𝒆𝒅 𝒆𝒍𝒆𝒎𝒆𝒏𝒕𝒔 𝒊𝒔 %𝒅", 𝒔𝒕𝒂𝒄𝒌[𝒕𝒐𝒑]);
𝒕𝒐𝒑 − −;
}
}](https://image.slidesharecdn.com/unit3stacksandqueues-240116110152-9d232533/75/Unit-3-Stacks-and-Queues-pptx-17-2048.jpg)
![Program Implementation of Stack Using Array
𝒗𝒐𝒊𝒅 𝒅𝒊𝒔𝒑𝒍𝒂𝒚()
{
𝒊𝒇(𝒕𝒐𝒑 >= 𝟎)
{
𝒑𝒓𝒊𝒏𝒕𝒇("𝒏 𝑻𝒉𝒆 𝒆𝒍𝒆𝒎𝒆𝒏𝒕𝒔 𝒊𝒏 𝑺𝑻𝑨𝑪𝑲 𝒏");
𝒇𝒐𝒓(𝒊 = 𝒕𝒐𝒑; 𝒊 >= 𝟎; 𝒊 − −)
𝒑𝒓𝒊𝒏𝒕𝒇("𝒏%𝒅", 𝒔𝒕𝒂𝒄𝒌[𝒊]);
𝒑𝒓𝒊𝒏𝒕𝒇("𝒏 𝑷𝒓𝒆𝒔𝒔 𝑵𝒆𝒙𝒕 𝑪𝒉𝒐𝒊𝒄𝒆");
}
𝒆𝒍𝒔𝒆
𝒑𝒓𝒊𝒏𝒕𝒇("𝒏 𝑻𝒉𝒆 𝑺𝑻𝑨𝑪𝑲 𝒊𝒔 𝒆𝒎𝒑𝒕𝒚");
}](https://image.slidesharecdn.com/unit3stacksandqueues-240116110152-9d232533/75/Unit-3-Stacks-and-Queues-pptx-18-2048.jpg)







![Algorithm to convert Infix to Postfix
• Step 4: If the scanned character is an ‘(‘ or ‘[‘ or ‘{‘, push it to the stack.
• Step 5: If the scanned character is an ‘)’or ‘]’ or ‘}’, pop the stack and output it until a
‘(‘ or ‘[‘ or ‘{‘ respectively is encountered, and discard both the parenthesis.
• Step 6: Repeat steps 2-6 until infix expression is scanned.
• Step 7: Print the output
• Step 8: Pop and output from the stack until it is not empty.](https://image.slidesharecdn.com/unit3stacksandqueues-240116110152-9d232533/75/Unit-3-Stacks-and-Queues-pptx-27-2048.jpg)







![Evaluation of prefix expression
Prefix Expression : - / * 20 * 50 + 3 6 300 2
Reversed Prefix Expression: 2 003 6 3 + 05 * 02 * / -
Token •
2 Reverse 2, Push 2 to stack [2]
3 Reverse 003, Push 300 to stack [2, 300]
6 Reverse 6, Push 6 to stack [2, 300, 6]
3 Reverse 3, Push 3 to stack [2, 300, 6, 3]
+
Pop 3 from stack [2, 300, 6]
Pop 6 from stack [2, 300]
Push 3+6 =9 to stack [2, 300, 9]
5 Reverse 05, Push 50 to stack
[2, 300, 9,
50]](https://image.slidesharecdn.com/unit3stacksandqueues-240116110152-9d232533/75/Unit-3-Stacks-and-Queues-pptx-39-2048.jpg)
![Evaluation of prefix expression
Prefix Expression : - / * 20 * 50 + 3 6 300 2
Reversed Prefix Expression: 2 003 6 3 + 05 * 02 * / -
Token •
Pop 50 from stack [2, 300, 9]
Pop 9 from stack [2, 300]
Push 50*9=450 to stack [2, 300, 450]
2 Reverse 02, Push 20 to stack
[2, 300, 450,
20]
*
Pop 20 from stack [2, 300, 450]
Pop 450 from stack [2, 300]
Push 20*450=9000 to stack
[2, 300,
9000]](https://image.slidesharecdn.com/unit3stacksandqueues-240116110152-9d232533/75/Unit-3-Stacks-and-Queues-pptx-40-2048.jpg)
![Evaluation of prefix expression
Prefix Expression : - / * 20 * 50 + 3 6 300 2
Reversed Prefix Expression: 2 003 6 3 + 05 * 02 * / -
Token •
/
Pop 9000 from stack [2, 300]
Pop 300 from stack [2]
Push 9000/300=30 to stack [2, 30]
-
Pop 30 from stack [2]
Pop 2 from stack []
Push 30-2=28 to stack [28]
Result : 28](https://image.slidesharecdn.com/unit3stacksandqueues-240116110152-9d232533/75/Unit-3-Stacks-and-Queues-pptx-41-2048.jpg)









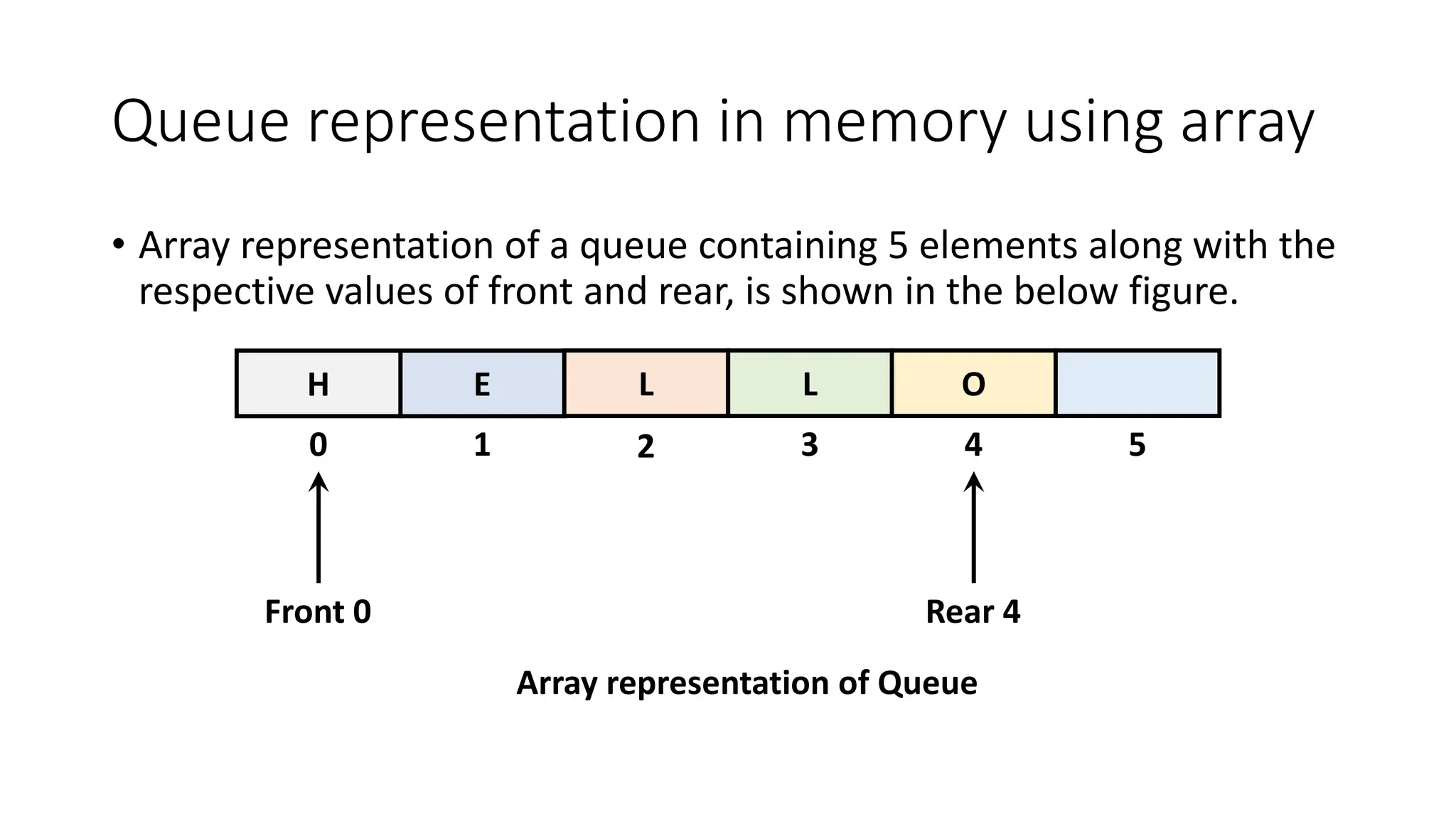
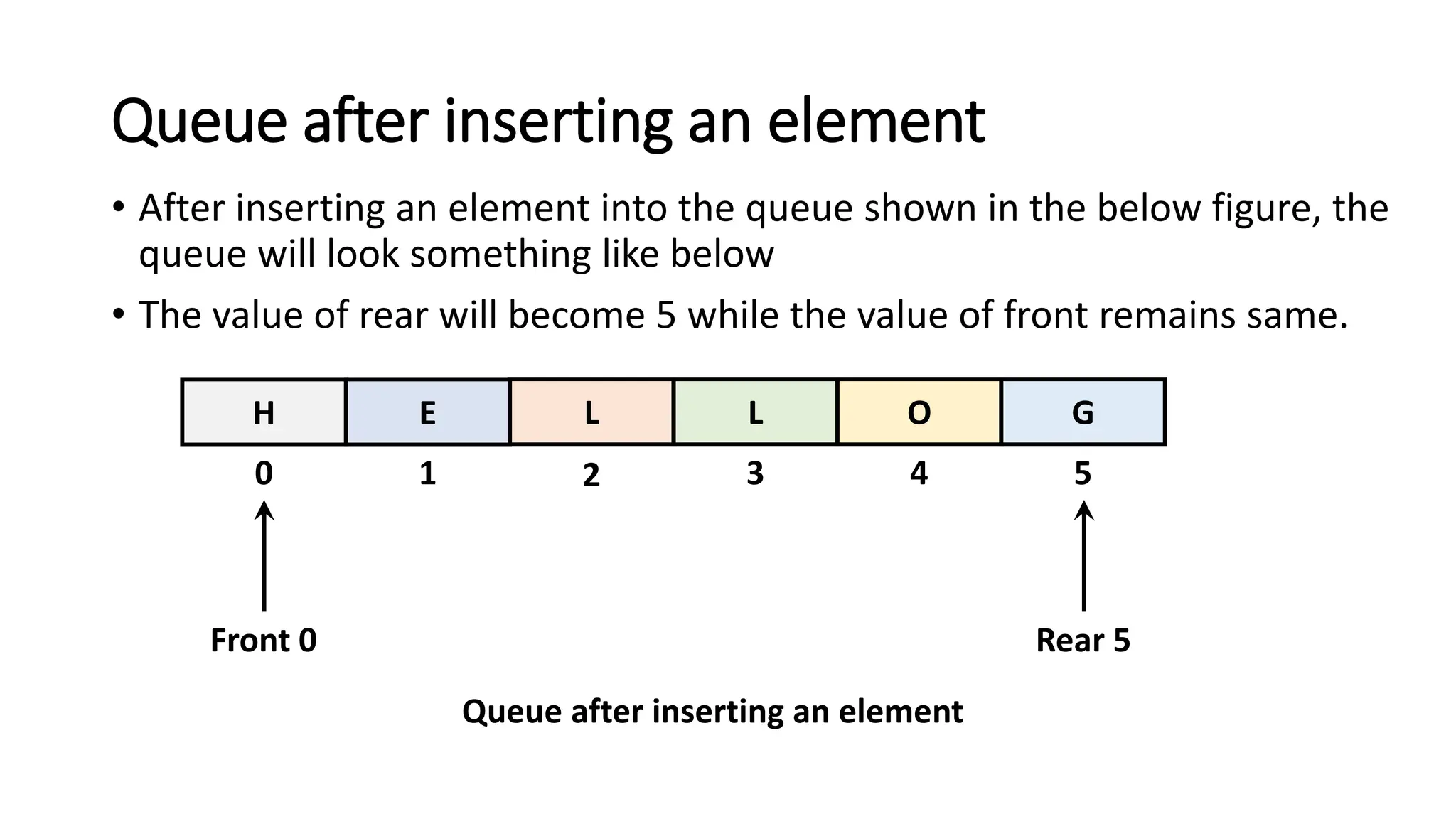

![Algorithm to insert any element in a queue
• Step 1: IF REAR = MAX - 1
Write OVERFLOW
Go to step
[END OF IF]
• Step 2: IF FRONT = -1 and REAR = -1
SET FRONT = REAR = 0
ELSE
SET REAR = REAR + 1
[END OF IF]
• Step 3: Set QUEUE[REAR] = NUM
• Step 4: EXIT](https://image.slidesharecdn.com/unit3stacksandqueues-240116110152-9d232533/75/Unit-3-Stacks-and-Queues-pptx-59-2048.jpg)
![Algorithm for Queue Operations
Let Q be the array of some specified size say SIZE
Inserting an element into the queue:
1. Initialize front=0 rear = –1
2. Input the value to be inserted and assign to variable “data”
3. If (rear >= SIZE)
a. Display “Queue overflow”
b. Exit
4. Else
a. Rear = rear +1
5. Q[rear] = data
6. Exit](https://image.slidesharecdn.com/unit3stacksandqueues-240116110152-9d232533/75/Unit-3-Stacks-and-Queues-pptx-60-2048.jpg)
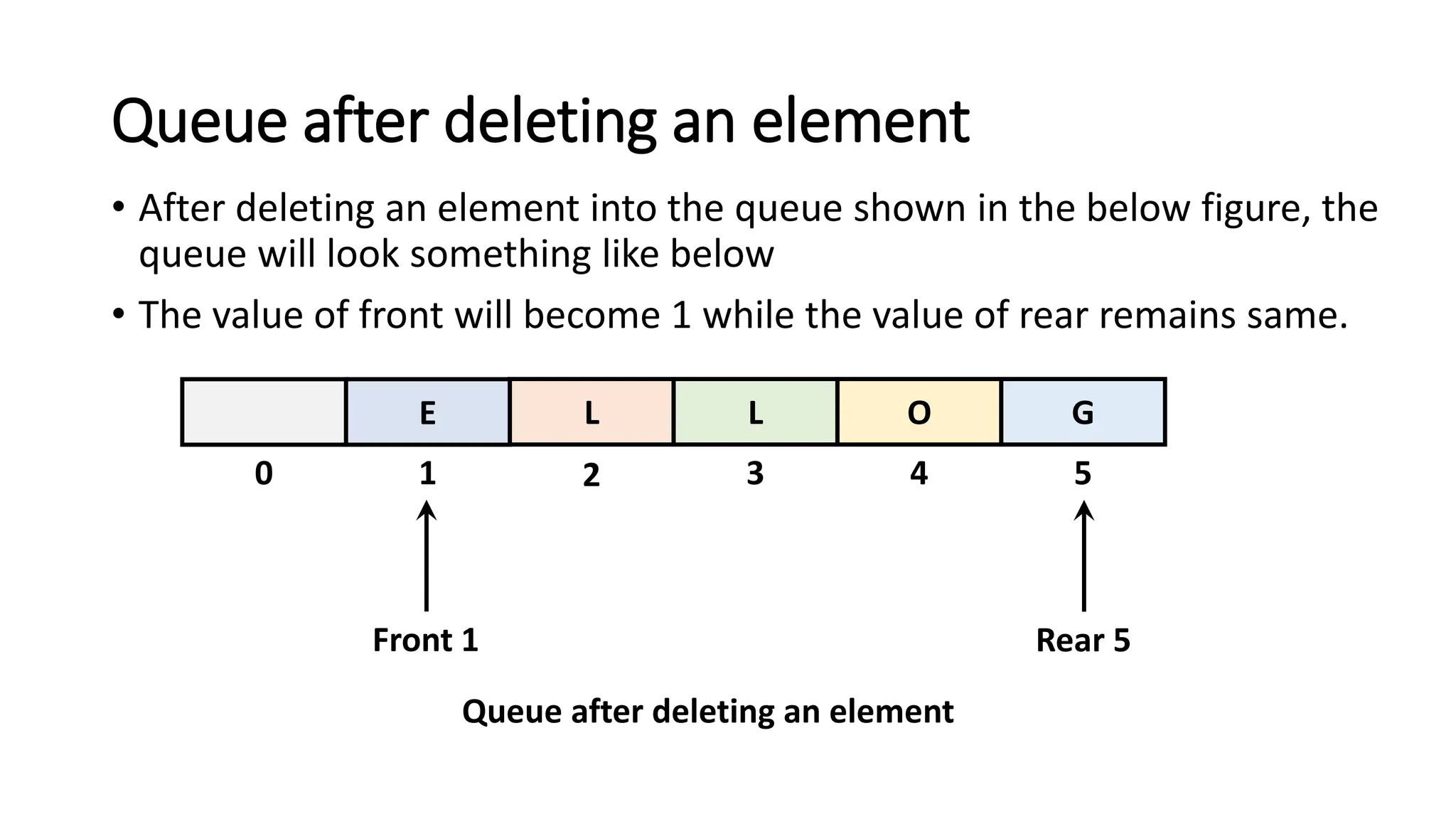

![Algorithm
• Step 1: IF FRONT = -1 or FRONT > REAR
Write UNDERFLOW
ELSE
SET VAL = QUEUE[FRONT]
SET FRONT = FRONT + 1
[END OF IF]
• Step 2: EXIT](https://image.slidesharecdn.com/unit3stacksandqueues-240116110152-9d232533/75/Unit-3-Stacks-and-Queues-pptx-63-2048.jpg)
![Algorithm for Queue Operations
Let Q be the array of some specified size say SIZE
Deleting an element into the queue:0
1. If (rear< front)
a. Front = 0, rear = –1
b. Display “The queue is empty”
c. Exit
2. Else
a. Data = Q[front]
3. Front = front +1
4. Exit](https://image.slidesharecdn.com/unit3stacksandqueues-240116110152-9d232533/75/Unit-3-Stacks-and-Queues-pptx-64-2048.jpg)




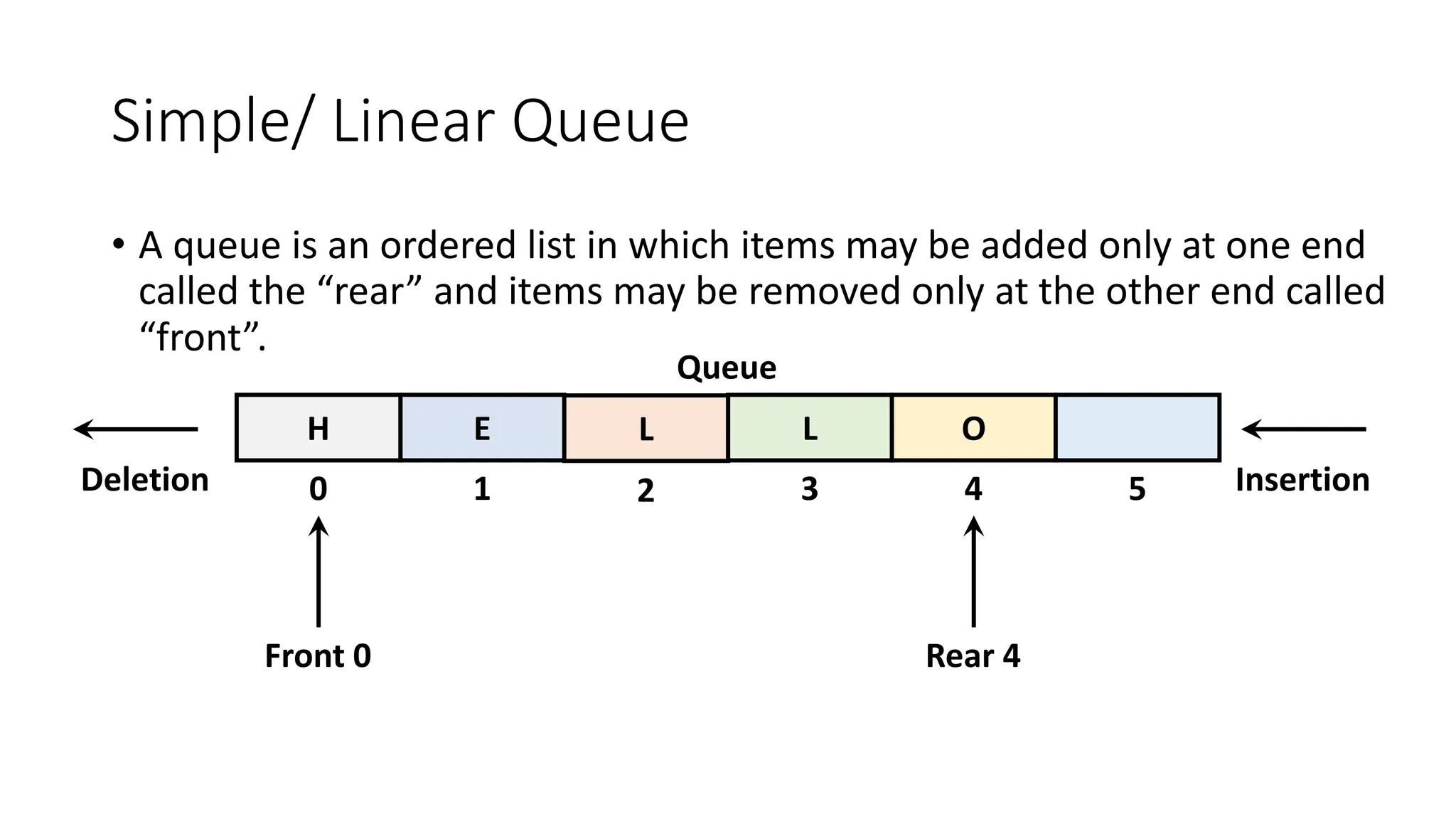

![Program: Implementation of linear queues using arrays
#𝑖𝑛𝑐𝑙𝑢𝑑𝑒 < 𝑠𝑡𝑢𝑑𝑖𝑜. ℎ >
#𝑖𝑛𝑐𝑙𝑢𝑑𝑒 < 𝑐𝑜𝑛𝑖𝑜. ℎ >
#𝑖𝑛𝑐𝑙𝑢𝑑𝑒 < 𝑠𝑡𝑑𝑙𝑖𝑏. ℎ >
#𝑑𝑒𝑓𝑖𝑛𝑒 𝑚𝑎𝑥𝑠𝑖𝑧𝑒 5
𝑖𝑛𝑡 𝑄𝑢𝑒𝑢𝑒 [𝑚𝑎𝑥𝑠𝑖𝑧𝑒];
𝑖𝑛𝑡 𝐹𝑟𝑜𝑛𝑡 = −1;
𝑖𝑛𝑡 𝑅𝑒𝑎𝑟 = −1;](https://image.slidesharecdn.com/unit3stacksandqueues-240116110152-9d232533/75/Unit-3-Stacks-and-Queues-pptx-71-2048.jpg)
![Program: Implementation of linear queues using arrays
𝑣𝑜𝑖𝑑 𝑖𝑛𝑠𝑒𝑟𝑡𝑖𝑜𝑛 ()
{
𝑖𝑛𝑡 𝑒𝑙𝑒;
𝑖𝑓(𝑅𝑒𝑎𝑟 == 𝑚𝑎𝑥𝑠𝑖𝑧𝑒 − 1)
{
𝑝𝑟𝑖𝑛𝑡𝑓("Queue is overflow n");
}
𝑒𝑙𝑠𝑒
{
𝑝𝑟𝑖𝑛𝑡𝑓("Enter an element: ");
𝑠𝑐𝑎𝑛𝑓("%d", &𝑒𝑙𝑒);
𝑅𝑒𝑎𝑟 = 𝑅𝑒𝑎𝑟 + 1;
𝑄𝑢𝑒𝑢𝑒[𝑅𝑒𝑎𝑟] = 𝑒𝑙𝑒;
𝑖𝑓(𝐹𝑟𝑜𝑛𝑡 == −1)
{
𝐹𝑟𝑜𝑛𝑡 = 0;
}
}
}](https://image.slidesharecdn.com/unit3stacksandqueues-240116110152-9d232533/75/Unit-3-Stacks-and-Queues-pptx-72-2048.jpg)
![Program: Implementation of linear queues using arrays
𝑣𝑜𝑖𝑑 𝑑𝑒𝑙𝑒𝑡𝑖𝑜𝑛 ()
{
𝑖𝑓(𝐹𝑟𝑜𝑛𝑡 == −1)
{
𝑝𝑟𝑖𝑛𝑡𝑓("Queue is under flown");
}
𝑒𝑙𝑠𝑒
{
𝑝𝑟𝑖𝑛𝑡𝑓(" Deleted element is: %d n", 𝑄𝑢𝑒𝑢𝑒 [𝐹𝑟𝑜𝑛𝑡]);
𝑖𝑓 (𝐹𝑟𝑜𝑛𝑡 == 𝑅𝑒𝑎𝑟)
{
𝐹𝑟𝑜𝑛𝑡 = −1;
𝑅𝑒𝑎𝑟 = −1;
}
𝑒𝑙𝑠𝑒
{
𝐹𝑟𝑜𝑛𝑡 = 𝐹𝑟𝑜𝑛𝑡 + 1;
}
}
}](https://image.slidesharecdn.com/unit3stacksandqueues-240116110152-9d232533/75/Unit-3-Stacks-and-Queues-pptx-73-2048.jpg)
![Program: Implementation of linear queues using arrays
𝑣𝑜𝑖𝑑 𝑑𝑖𝑠𝑝𝑙𝑎𝑦 ()
{
𝑖𝑛𝑡 𝑖;
𝑖𝑓 (𝐹𝑟𝑜𝑛𝑡 == −1)
{
𝑝𝑟𝑖𝑛𝑡𝑓(“𝑄𝑢𝑒𝑢𝑒 𝑖𝑠 𝑢𝑛𝑑𝑒𝑟 𝑓𝑙𝑜𝑤 n”);
}
𝑒𝑙𝑠𝑒
{
𝑓𝑜𝑟(𝑖 = 𝐹𝑟𝑜𝑛𝑡; 𝑖 <= 𝑅𝑒𝑎𝑟; 𝑖 + +)
{
𝑝𝑟𝑖𝑛𝑓𝑡(“%5𝑑”, 𝑄𝑢𝑒𝑢𝑒[𝑖]);
}
𝑝𝑟𝑖𝑛𝑡𝑓(“n”);
}
}](https://image.slidesharecdn.com/unit3stacksandqueues-240116110152-9d232533/75/Unit-3-Stacks-and-Queues-pptx-74-2048.jpg)


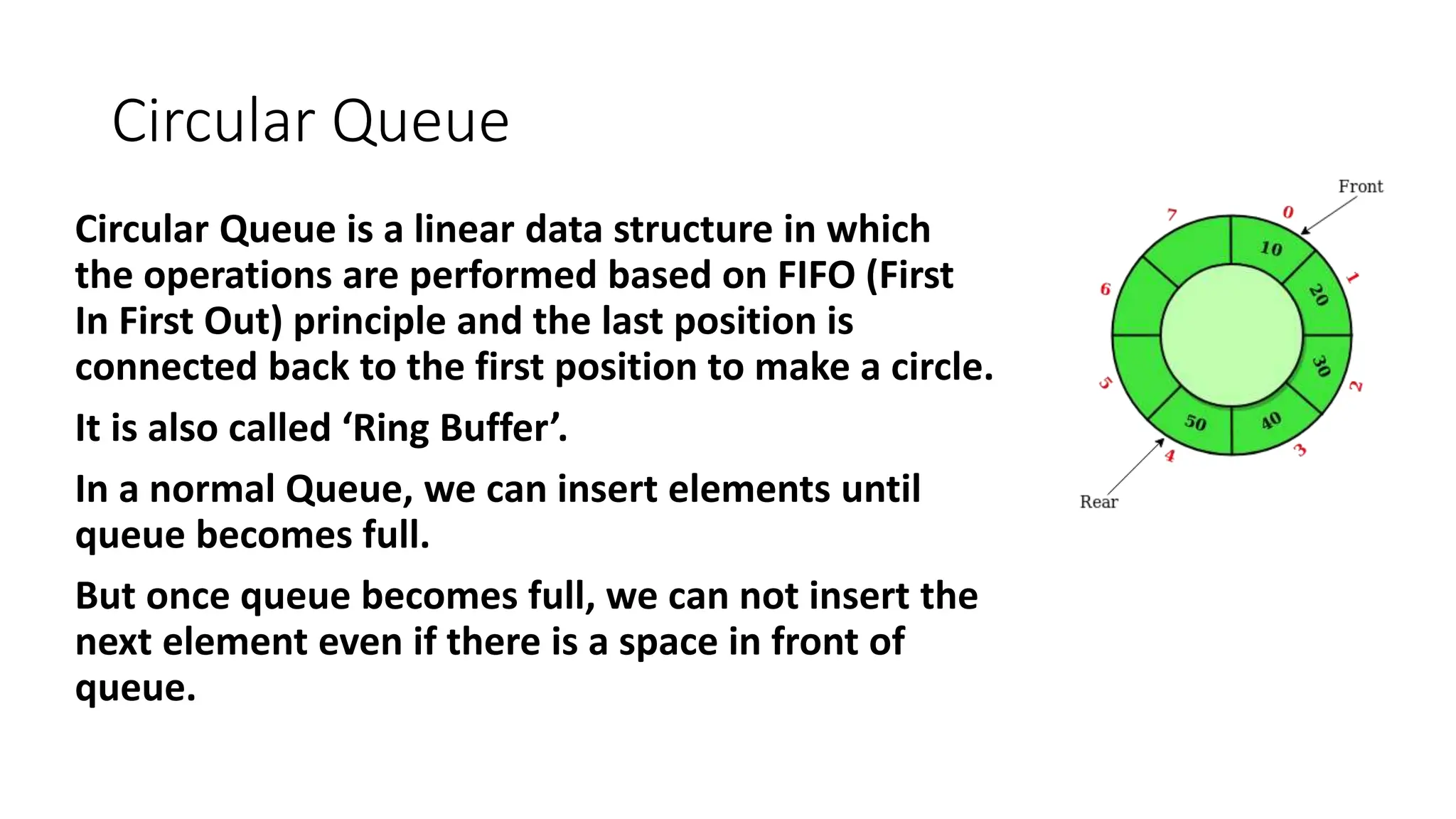
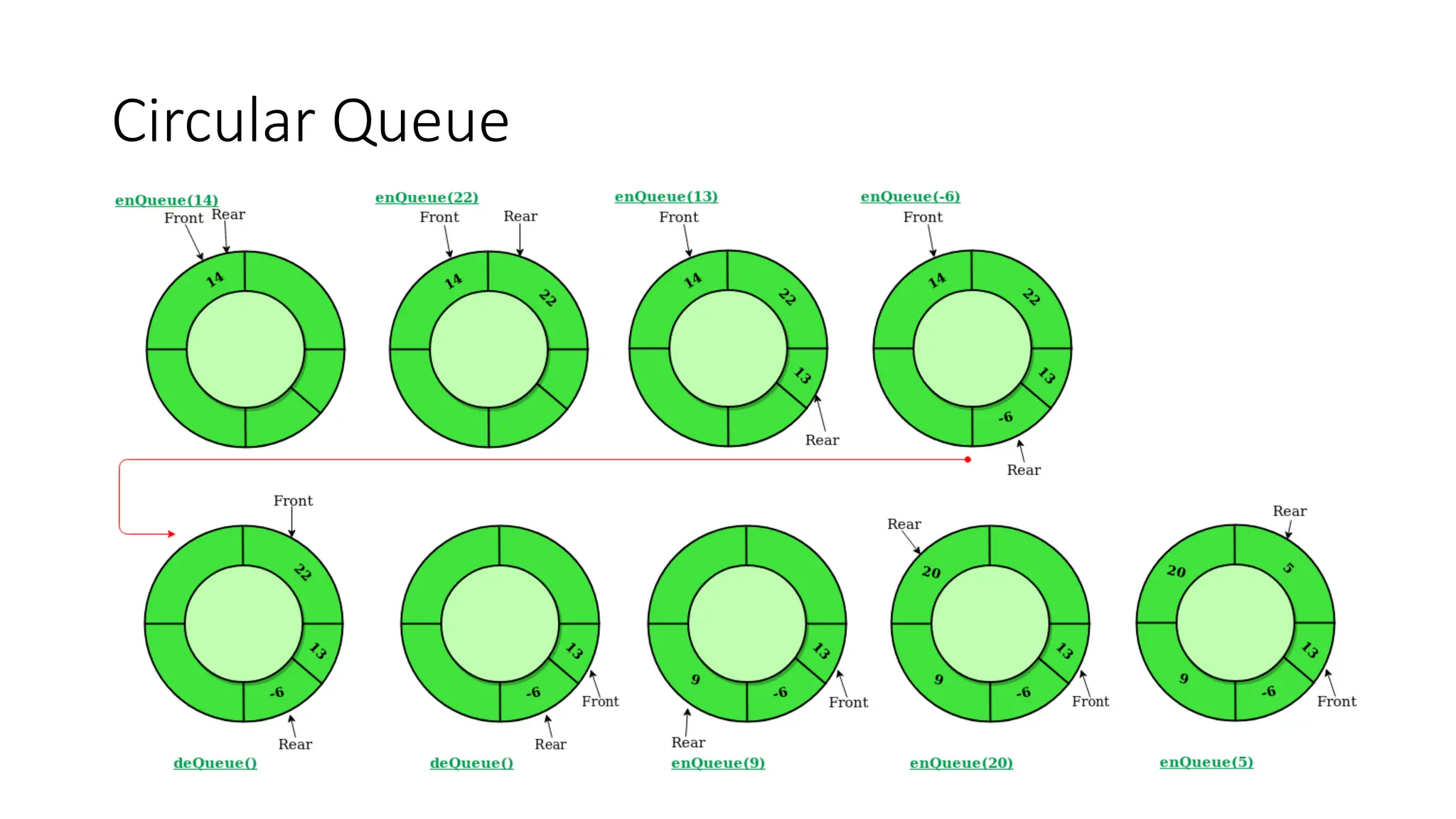



![Program: Implementation of circular queue
#𝑖𝑛𝑐𝑙𝑢𝑑𝑒 < 𝑠𝑡𝑑𝑖𝑜. ℎ >
# 𝑑𝑒𝑓𝑖𝑛𝑒 𝑀𝐴𝑋 5
𝑖𝑛𝑡 𝑐𝑞𝑢𝑒𝑢𝑒_𝑎𝑟𝑟[𝑀𝐴𝑋];
𝑖𝑛𝑡 𝑓𝑟𝑜𝑛𝑡 = −1;
𝑖𝑛𝑡 𝑟𝑒𝑎𝑟 = −1;](https://image.slidesharecdn.com/unit3stacksandqueues-240116110152-9d232533/75/Unit-3-Stacks-and-Queues-pptx-82-2048.jpg)
![Program: Implementation of circular queue
𝑣𝑜𝑖𝑑 𝑖𝑛𝑠𝑒𝑟𝑡(𝑖𝑛𝑡 𝑖𝑡𝑒𝑚)
{
𝑖𝑓((𝑓𝑟𝑜𝑛𝑡 == 0 && 𝑟𝑒𝑎𝑟 == 𝑀𝐴𝑋 − 1) || (𝑓𝑟𝑜𝑛𝑡 == 𝑟𝑒𝑎𝑟 + 1))
{
𝑝𝑟𝑖𝑛𝑡𝑓("Queue Overflow n");
𝑟𝑒𝑡𝑢𝑟𝑛;
}
𝑖𝑓(𝑓𝑟𝑜𝑛𝑡 == −1)
{
𝑓𝑟𝑜𝑛𝑡 = 0;
𝑟𝑒𝑎𝑟 = 0;
}
𝑒𝑙𝑠𝑒
{
𝑖𝑓(𝑟𝑒𝑎𝑟 == 𝑀𝐴𝑋 − 1)
𝑟𝑒𝑎𝑟 = 0;
𝑒𝑙𝑠𝑒
𝑟𝑒𝑎𝑟 = 𝑟𝑒𝑎𝑟 + 1;
}
𝑐𝑞𝑢𝑒𝑢𝑒_𝑎𝑟𝑟[𝑟𝑒𝑎𝑟] = 𝑖𝑡𝑒𝑚 ;
}](https://image.slidesharecdn.com/unit3stacksandqueues-240116110152-9d232533/75/Unit-3-Stacks-and-Queues-pptx-83-2048.jpg)
![Program: Implementation of circular queue
𝑣𝑜𝑖𝑑 𝑑𝑒𝑙𝑒𝑡𝑖𝑜𝑛()
{
𝑖𝑓(𝑓𝑟𝑜𝑛𝑡 == −1)
{
𝑝𝑟𝑖𝑛𝑡𝑓("Queue Underflown");
𝑟𝑒𝑡𝑢𝑟𝑛 ;
}
𝑝𝑟𝑖𝑛𝑡𝑓("Element deleted from queue is ∶ %dn", 𝑐𝑞𝑢𝑒𝑢𝑒_𝑎𝑟𝑟[𝑓𝑟𝑜𝑛𝑡]);
𝑖𝑓(𝑓𝑟𝑜𝑛𝑡 == 𝑟𝑒𝑎𝑟)
{
𝑓𝑟𝑜𝑛𝑡 = −1;
𝑟𝑒𝑎𝑟 = −1;
}
𝑒𝑙𝑠𝑒
{
𝑖𝑓(𝑓𝑟𝑜𝑛𝑡 == 𝑀𝐴𝑋 − 1)
𝑓𝑟𝑜𝑛𝑡 = 0;
𝑒𝑙𝑠𝑒
𝑓𝑟𝑜𝑛𝑡 = 𝑓𝑟𝑜𝑛𝑡 + 1;
}
}](https://image.slidesharecdn.com/unit3stacksandqueues-240116110152-9d232533/75/Unit-3-Stacks-and-Queues-pptx-84-2048.jpg)
![Program: Implementation of circular queue
𝑣𝑜𝑖𝑑 𝑑𝑖𝑠𝑝𝑙𝑎𝑦()
{
𝑖𝑛𝑡 𝑓𝑟𝑜𝑛𝑡_𝑝𝑜𝑠 = 𝑓𝑟𝑜𝑛𝑡 = 𝑟𝑒𝑎𝑟;
𝑖𝑓(𝑓𝑟𝑜𝑛𝑡 == −1)
{
𝑝𝑟𝑖𝑛𝑡𝑓("Queue is emptyn");
𝑟𝑒𝑡𝑢𝑟𝑛;
}
𝑝𝑟𝑖𝑛𝑡𝑓("Queue elements ∶ n");
𝑖𝑓(𝑓𝑟𝑜𝑛𝑡_𝑝𝑜𝑠 <= 𝑟𝑒𝑎𝑟_𝑝𝑜𝑠)
𝑤ℎ𝑖𝑙𝑒(𝑓𝑟𝑜𝑛𝑡_𝑝𝑜𝑠 <= 𝑟𝑒𝑎𝑟_𝑝𝑜𝑠)
{
𝑝𝑟𝑖𝑛𝑡𝑓("%d ", 𝑐𝑞𝑢𝑒𝑢𝑒_𝑎𝑟𝑟[𝑓𝑟𝑜𝑛𝑡_𝑝𝑜𝑠]);
𝑓𝑟𝑜𝑛𝑡_𝑝𝑜𝑠 + +;
}](https://image.slidesharecdn.com/unit3stacksandqueues-240116110152-9d232533/75/Unit-3-Stacks-and-Queues-pptx-85-2048.jpg)
![Program: Implementation of circular queue
𝑒𝑙𝑠𝑒
{
𝑤ℎ𝑖𝑙𝑒(𝑓𝑟𝑜𝑛𝑡_𝑝𝑜𝑠 <= 𝑀𝐴𝑋 − 1)
{
𝑝𝑟𝑖𝑛𝑡𝑓("%d ", 𝑐𝑞𝑢𝑒𝑢𝑒_𝑎𝑟𝑟[𝑓𝑟𝑜𝑛𝑡_𝑝𝑜𝑠])
𝑓𝑟𝑜𝑛𝑡_𝑝𝑜𝑠 + +;
}
𝑓𝑟𝑜𝑛𝑡_𝑝𝑜𝑠 = 0;
𝑤ℎ𝑖𝑙𝑒(𝑓𝑟𝑜𝑛𝑡_𝑝𝑜𝑠 <= 𝑟𝑒𝑎𝑟_𝑝𝑜𝑠)
{
𝑝𝑟𝑖𝑛𝑡𝑓("%d ", 𝑐𝑞𝑢𝑒𝑢𝑒_𝑎𝑟𝑟[𝑓𝑟𝑜𝑛𝑡_𝑝𝑜𝑠]);
𝑓𝑟𝑜𝑛𝑡_𝑝𝑜𝑠 + +;
}
}
𝑝𝑟𝑖𝑛𝑡𝑓("n");
}](https://image.slidesharecdn.com/unit3stacksandqueues-240116110152-9d232533/75/Unit-3-Stacks-and-Queues-pptx-86-2048.jpg)





