String matching algorithms

String matching algorithms

• 1.
  • Shashikant V. Athawale AssistantProfessor ,Computer Engineering Department AISSMS College of Engineering, Kennedy Road, Pune , MS, India - 411001
• 3.
   Definitions - FormalDefinition of String Matching Problem- Formal Definition of String Matching Problem - Assume text is an array T[1..n] of length n and- Assume text is an array T[1..n] of length n and the pattern is an array P[1..m] of length m ≤ nthe pattern is an array P[1..m] of length m ≤ n Explanation:Explanation: This basically means that there is a string array T which contains a certainThis basically means that there is a string array T which contains a certain number of characters that is larger than the number of characters in stringnumber of characters that is larger than the number of characters in string array P. P is said to be the pattern array because it contains a pattern ofarray P. P is said to be the pattern array because it contains a pattern of characters to be searched for in the larger array T.characters to be searched for in the larger array T.
• 4.
   Definitions - Strings-Strings -- ΣΣ* denotes the set of all finite length strings* denotes the set of all finite length strings formed by using characters from the alphabetformed by using characters from the alphabet - The zero length empty string denoted by- The zero length empty string denoted by εε andand is a member ofis a member of ΣΣ** - The length of a string x is denoted by |x|- The length of a string x is denoted by |x| - The concatenation of two strings x and y,- The concatenation of two strings x and y, denoted xy, has length |x| + |y| and consists ofdenoted xy, has length |x| + |y| and consists of the characters in x followed by the characters inthe characters in x followed by the characters in yy
• 5.
  Example:
• 6.
  •There are differentsolutions that allow to solve the string matching problem. 1. Naive Algorithm 2. Knuth-Morris-Pratt Algorithm (KMP) 3. Boyer-Moore Algorithm (BM) 4. Rabin-Karp Algorithm (RK)
• 7.
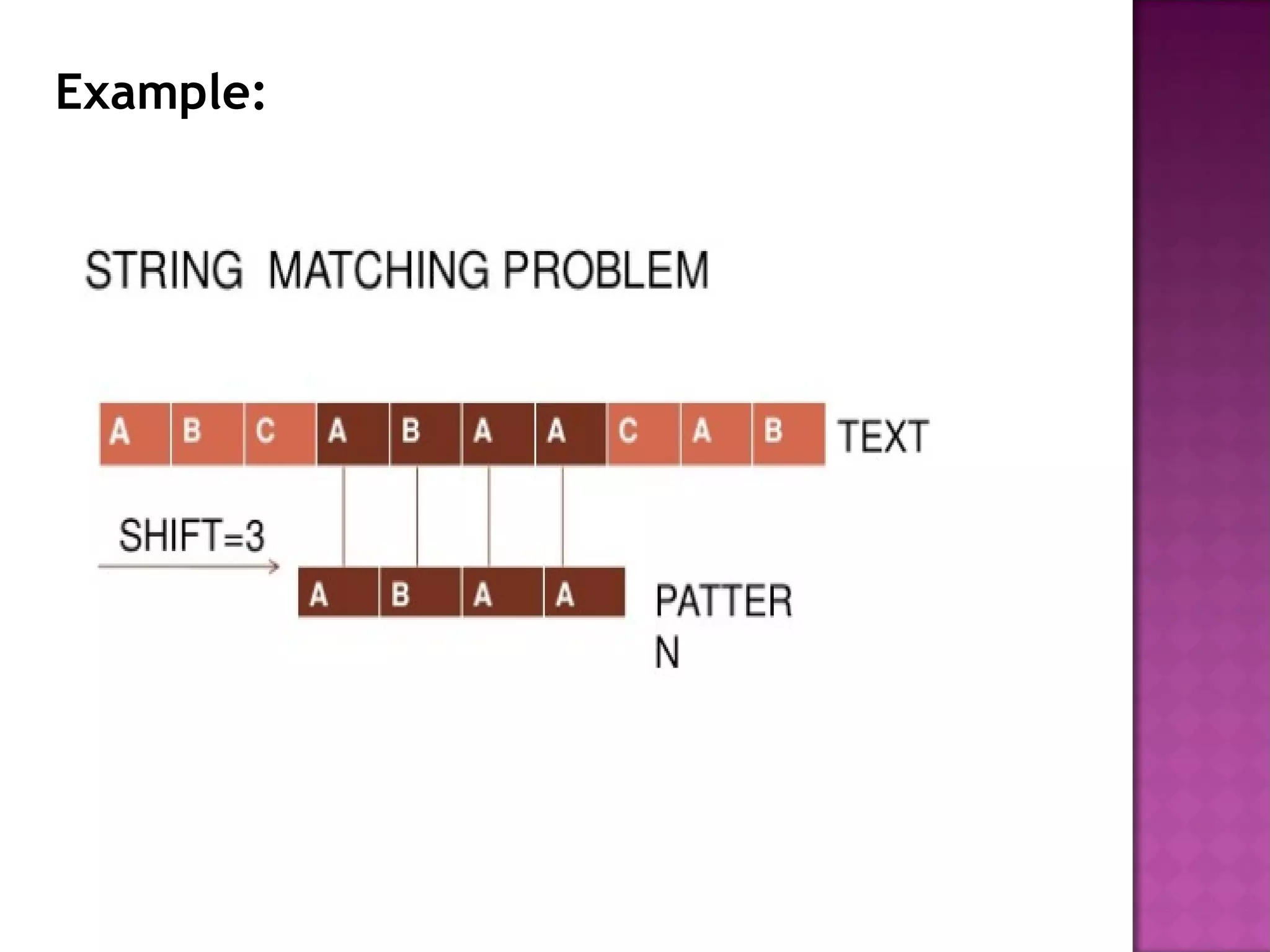
  1.Naive Algorithm The ideaof the naive solution is just to make a comparison character by character of the text T[s...s + m − 1] for all s {0, . . . , n − m + 1}∈ and the pattern P[0...m − 1]. It returns all the valid shifts found. Figure 2 shows how the algorithm work in a practical example.  For example if the pattern to search is a m and the text is a n, then we need M operation of comparison by shift. For all the text, we need (N − M + 1) × M operation, generally M is very small compared to N, it is why we can simply considered the complexity as O(M × N). 2
• 8.
  In Figure 3is an implementation written in pseudo-code of the naive algorithm. The problem of this approach is the effectiveness. In fact, the time complexity of the Naive algorithm in its worst case is O(M × N).
• 9.
  2. Knuth-Morris-Pratt Algorithm(KMP) The KMP algorithm is a linear time algorithm, more accurately O(N + M).  The main characteristic of KMP is each time when a match between the pattern and a shift in the text fails, the algorithm will use the information given by a specific table, obtained by a preprocessing of the pattern, to avoid re-examine the characters that have been previously checked, thus limiting the number of comparison required.  So KMP algorithm is composed by two parts, a searching part which consists to find the valid shifts in the text, where the time complexity is O(N), obtained by comparison of the pattern and the shifts of the text, and a preprocessing part which consists to preprocesse the pattern.
• 10.
  The complexity ofthe preprocessing part is O(M), applying the same serching algorithm to pattern itself. In Figure 4 there is an example where we need three attempts to find a valid shift, whereas with the naive solution, we need four attempts, we could not skip the shift at the position one.
• 11.
  3. Boyer-Moore Algorithm(BM) The basic idea behind this solution is that the match is performed from right to left. This characteristic allows the algorithm to skip more characters than the other algorithms, for example if the first character matched of the text is not contained in the pattern P[0...m − 1], we can skip m characters immediately. As the KMP algorithm, this algorithm preprocesses the pattern to obtain a table which contains information to skip characters for each character of the pattern. But BM algorithm use also another table based on the alphabet. It contains as many entries as there are characters in the alphabet . In the example below, we can easily persuade the advantage of BM algorithm over KMP and the naive one, we only need four attempts to find the valid shift.
• 12.
  In this case,the time complexity of the BM algorithm is sublinear: O(N/M). In the worst case, the complexity of the algorithm is O(N × M), it happens for example when the size of the alphabet is one, or more generally when the pattern and the text are strings composed by sequences of one same character.
• 13.
  4. Rabin-Karp Algorithm (RK) TheRabin-Karp algorithm uses a totally different approach to solve the string matching problem. This method is based on hashing techniques. We compute a hash function h(x) for the pattern P[0...m−1] and then look for a match by using the same hash function for each substring of length m − 1 of the text . The Rabin-Karp also use preprocessing technique before the search operation. Its preprocessing operation is the hashing of the pattern, which is O(M) complexity. So, the running time of the algorithm is O(M × (N − M + 1)), but in general, we will see, that the algorithms will run with a complexity O(N).  Let’s introduce following notations: • h(p) : the hashed value of the pattern • h(ts) : the hashed value of the substring [s, ..., s + M − 1]
• 14.
  Example  if wehave P =“cd” and T = “abcd”. Based on the implementation, we can easily obtained h(p) = 99 · 2 + 100 = 298, where 99 and 100 are respectively the integer value of c and d in ASCII representation. We compute h(t0) = 292 in the same way, we can see that h(p) 6= h(t0), so we will use the REHASH function to compute h(t1) = 295. This value does not match with h(p) too, so we compute h(t2) = 298, it matches with h(p), but we still need to check character by character to avoid collisions.