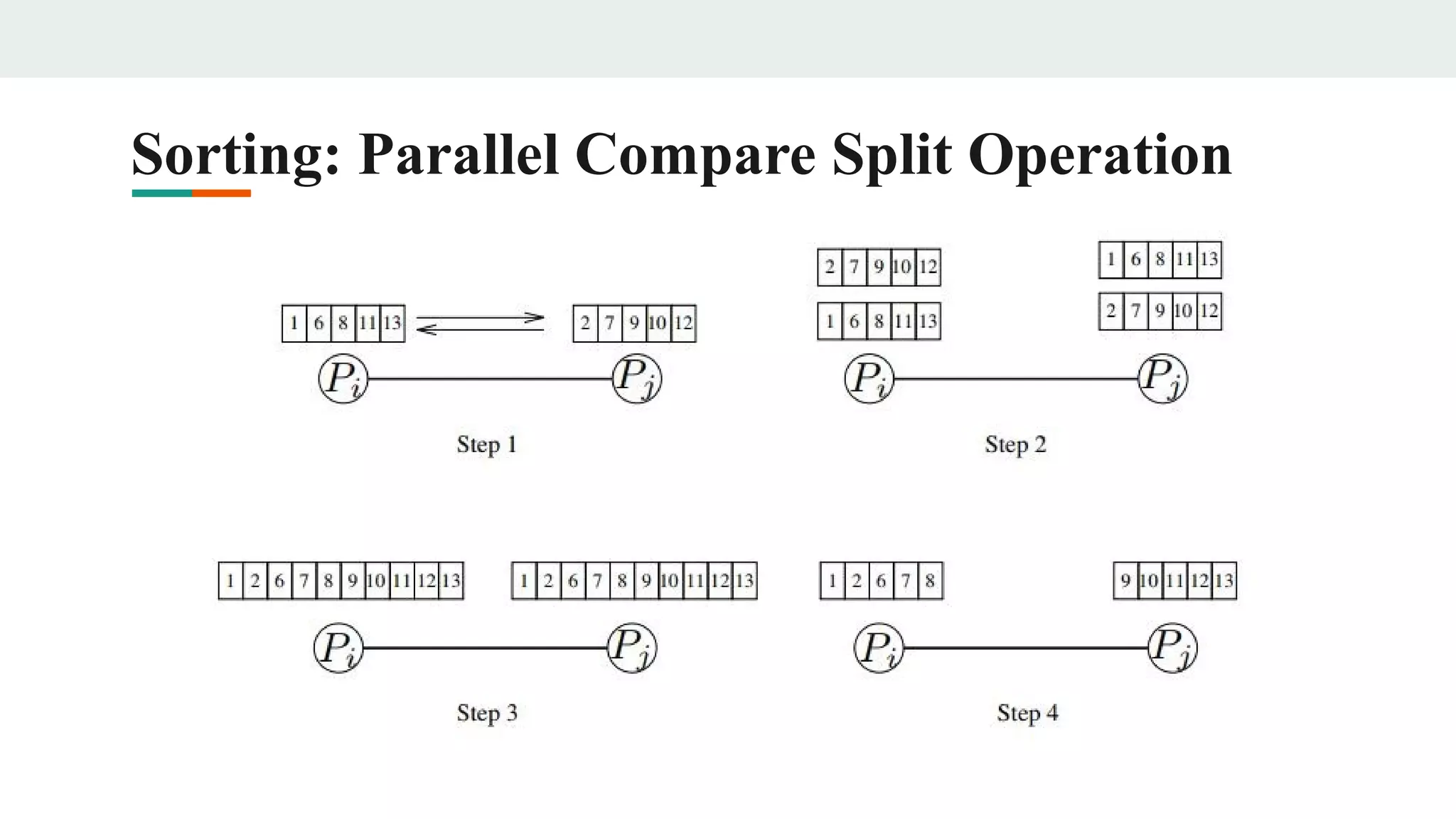
This document discusses parallel algorithms for sorting and graph problems. It covers parallel implementations of sorting algorithms like bubble sort, quicksort, and parallel compare-exchange and compare-split operations. For graphs, it discusses parallel depth-first search by partitioning the search space, all-pairs shortest paths problems, and algorithms for sparse graphs. It also briefly mentions parallel breadth-first search and parallel best-first search.