Chapter 1 FEM in 1 Dimension
Simple case: Solution domain is divided into a number of intervals called finite
elements, and the solution itself is approximated with a linear function over each
element. The union of the linear element functions yields a continuous, piecewise
linear function.
1.1 Steady diffusion with linear elements.
Steady heat conduction through a rod of length L, in the presence of a distributed
source of heat due to a chemical reaction. Fick’s law:
df
q x k , k is the thermal conductivity of the rod material, and f(x) is the
dx
temperature. A heat balance over a section of the rod with infinitesimal length x
requires
q x q x x s x x 0 , s(x) is the rate of heat production.
k df df
s x 0
x dx x dx x x
Taking x
d2 f
k s x 0.
dx 2
Boundary conditions:
1) heat flux at the left end of the rod located at x=0
df
q0 k , q0 is a given constant (Neumann boundary condition)
dx x 0
2) temperature at the right end of the rod located at x=L
f x L f L . (Dirichlet boundary condition)
1.1.1 Linear element interpolation
I
�Dividing the solution domain, 0 x L into NE intervals, called finite elements,
defined by the element end-nodes, xi , for i 1, 2,...., NE 1 , where x1 0 , and
xN E 1 L.
Next, we approximate the temperature distribution over the individual elements
with linear functions whose union yields a continuous, piecewise linear function.
Piecewise linear, tent-like, global interpolation functions i x , i 1, 2,..., N E 1,
where the i th function is supported over the interval xi 1 , xi 1 . The i th
interpolation function takes the value of unity at the i th nodes, drops linearly to
zero at the adjacent nodes numbered i-1 and i+1, and remains zero outside the
supporting interval xi 1 , xi 1 . By construction, the global interpolation functions
satisfy the cardinal interpolation property
i xj ij .
The piecewise linear approximation of the solution is represented by the global
finite element expansion
II
� NE 1
f x fj j x , fj f x x j is the a priori unknown value of the solution at
j 1
the j th nodes. f N E 1 fL
Piecewise linear taking second derivative, we are faced with zero function
bypassed by seeking a solution of the weak formulation, which arises from the
Galerkin projection of the differential equation.
PS: A continuous function with discontinuous first derivative at discrete points is
called C 0 function. A continuous function with continuous first derivative and
discontinuous second derivative at discrete points is called C1 function.
1.1.2 Element grading
Two important features of FEM are (a) ability to ensure adequate spatial
resolution by varying the element size manually or adaptively, (b) ease for
accommodating irregular geometrical shapes.
xN
ratio
x1
1.1.3 Galerkin projection
Galerkin finite element method (GFEM)
We multiply both sides of the governing equation by each one of the global
interpolation functions i for i 1, 2,...., N E and integrate the product over the
solution domain to obtain the Galerkin projection
L d2 f
i x k 2 s x dx 0
0 dx
Note: Because of Dirichlet BC, the last global interpolation function,
corresponding to i NE 1 is excluded in the projection.
III
� L d df df d i
k i k i s dx 0,
0 dx dx dx dx
df df L d i df L
i x 0 k i x L k k dx i sdx 0
dx x 0 dx x L
0 dx dx 0
df df L d i df L
i1 k i, NE 1 k k dx i sdx 0.
dx x 0 dx x L
0 dx dx 0
No contribution
L d i df L
i1 0 q k dx i sdx 0
0 dx dx 0
L d i df q0 1 L
dx i1 i sdx 0
0 dx dx k k 0
1.1.4 Formulation of a linear algebraic system
NE 1
Note: s x sj j x , where s j s x xj .
j 1
Rearranging the resulting equation, we derive a system of NE linear equations
for the NE unknown values f j .
NE
L d i d j L d i d N1 q0 1 NE 1 L
dx f j dx f L i1 i j dx s j 0 , where
j 1
0 dx dx 0 dx dx k k j1 0
i 1, 2,..., N E .
IV
� 1 0 x xi 1
i x xi 1 , for xi 1 x xi
xi xi 1 hi 1
0 1 xi 1 x
i x xi 1 , for xi x xi 1
xi 1 xi hi 1
d i 1
, for xi 1 x xi
dx hi 1
d i 1
, for xi x xi 1
dx hi 1
If i j 1 and N E 1
L d i d j xi 1 d i d i xi 1 1 xi 1 1 1 1 1
Dij dx dx dx dx
0 dx dx xi 1 dx dx xi 1 h
i 1 hi 1
xi hi hi hi 1 hi
If j i 1
L d i d j xi 1 d i d i1 xi 1 1 xi 1 1 1
dx dx dx 0dx
0 dx dx xi 1 dx dx xi 1 h
i 1 hi
xi hi hi
V
�If j i 1
L d i d j xi 1 d i d i1 xi 1 xi 1 1 1 1
dx dx 0dx dx
0 dx dx xi 1 dx dx xi 1 h
i 1
xi hi hi 1 hi 1
If i j 1
L d i d j xi 1 d 1d 1 x2 1 1 1
dx dx dx
0 dx dx xi 1 dx dx x1 h1 h1 h1
If i j NE 1
L d i d j xi 1 d N 1 d N 1
xi 1 1 1
dx dx dx
0 dx dx xi 1 dx dx xi 1 h h
N N hN
Otherwise
L d i d j
dx 0
0 dx dx
If i j 1 and N E 1
L xi 1 xi x xi 1 x xi 1
xi 1 xi 1 x xi 1 x
M ij i j dx i i dx dx dx
0 xi 1 xi 1 hi 1 hi 1
xi hi hi
2 2
1 xi 2 1 xi 1 2
x xi 1 dx x xi 1 dx
hi 1 xi 1 hi xi
2 2
1 hi 1 2 1 hi
x dx x 2 dx
hi 1 0 hi 0
hi 1 hi
3 3
Substituting these values in the above, we derive the linear system
D f b , where
f is the vector of the unknown temperatures at the nodes,
VI
� f1
f2
f ... .
f NE 1
f NE
D is N E N E global diffusion or conducting matrix, given by
1 1
0 0 ... 0 0 0
h1 h1
1 1 1 1
0 ... 0 0 0
h1 h1 h2 h2
... ... ... ... ... ... ... ...
1 1 1 1
0 0 0 ... 0
D hi 1 hi 1 hi hi
... ... ... ... ... ... ... ...
... ... ... ... ... ... ... ...
1 1 1 1
0 0 0 ... 0
hN E 2 hN E 2 hN E 1 hN E 1
1 1 1
0 0 0 ... 0 0
hN E 1 hN E 1 hN E
The right-hand side of the linear system is given by
1
b c M s , where the nearly null NE dimensional vector c encapsulates the
k
boundary conditions
q0 / k
0
c ...
0
f L / hN E
M is the N E NE 1 bordered mass matrix given by
VII
� h1 h1
0 0 ... 0 0 0
3 6
h1 h1 h2 h2
0 ... 0 0 0
6 3 3 6
... ... ... ... ... ... ... ...
hi 1 hi 1 hi hi
0 0 0 ... 0
M 6 3 3 6
... ... ... ... ... ... ... ...
... ... ... ... ... ... ... ...
hN E 2 hN E 2 hN E 1 hN E 1
0 0 0 0 0
6 3 3 6
hN E 1 hN E 1 hN E hN E
0 0 0 ... 0
6 3 3 6
and N E 1 -dimensional vector s, contains the nodal values of the source
s1
s2
s ... .
sN E
sN E 1
Note that the global diffusion matrix has units of inverse length, whereas the
global mass matrix has units of length.
Explicitly, the right-hand side of the linear system is given by
h1 h1
s1 s
3 6
h1 h1 h2 h2
s1 s2 s3
6 3 3 6
1 ...
b c
k h hN E hN E hN E
NE 2 2 1 1
sN 2 sN 1 sN
6 3 3 6
hN E 1 hN E 1 hN E hN E
sN 1 sN sN 1
6 3 3 6
VIII
� Tridiagonal matrix solved by Thomas algorithm
Cf) Comparison with FDM
1.1.8 Element diffusion and mass matrices
In the practical implementation of the finite element method, the integrals arising
from the Galerkin projection are assembled from corresponding integrals over the
elements in a systematic way that facilitates the bookkeeping.
NE 1 NE
d i d j NE 1 NE
k dx f j q0 j1 i j dx s j , where El stands for the
j 1 l 1
El dx dx j 1 l 1
El
l th element subtended between xl and xl 1 .
Because the support of the global interpolation functions is compact,
d i d j d l d j d l1d j
dx il dx i ,l 1 E dx
El dx dx El dx dx l dx dx
d l d l d l d l1
il jl E dx j ,l 1 E dx
l dx dx l dx dx
d l1d l d l1d l1
i ,l 1 jl dx j ,l 1 E dx
El dx dx l dx dx
In compact notation
d i d j l l l l
dx il jl A11 il i, j 1 A12 i ,l 1 jl A21 i ,l 1 j ,l 1 A22 ,
El dx dx
l
where Ain is the l th-element diffusion matrix with components
l l
l d l d l d 1 d 1
A 11 dx dx
El dx dx El dx dx
l l
l l d l d l1 d 1 d 2
A 12 A21 dx dx
El dx dx El dx dx
l l
l d l1d l1 d 2 d 2
A22 dx dx
El dx dx El dx dx
IX
�Carrying out the integrations,
l l
l A11 A12 1 1 1
A
A
l
21 A
l
22
hl 1 1
For the mass matrix
l l l l
i j dx il jl B11 il i, j 1 B12 i ,l 1 jl B21 i ,l 1 j ,l 1 B22
El
l l
l B11 B12 hl 2 1
B
B21
l
B22
l
6 1 2
NE
l l l l
il A11 fl A12 fl 1 i ,l 1 A21 fl A22 fl 1
l 1
NE
q0 1 l l l l
i1 il B11 sl B12 sl 1 i ,l 1 B21 sl A22 sl 1
k k l 1
Note: lth element contributes only to the Galerkin-projection equations for i=l and
l+1. thus, first element corresponding to l=1 contributes to the first and second
equations associated with the projections of 1 and 2 , and the second element
corresponding to l-2 contributes to the second and third equations associated
with the projections of 2 and 3 . The linear system can be assembled by
scanning elements one by one, while making appropriate additive contributions
to the coefficient matrices on the left- and right-hand sides.
X
� 1 1
A11 A12 0 0 ... 0 0 0
1 1 2 2
A21 A22 A11 A12 0 ... 0 0 0
2 2 3 3
0 A 21 A 22 A
11 A12 ... ... ... ...
0 0 ... ... ... ... ... 0
D
... ... ... ... ... ... ... ...
N 3 N 3 N 2 N 2
... ... ... ... A21 e A22 e A12 e A21 e 0
N 2 N 2 N 1 N 1
0 0 0 ... 0 A21 e A22 e A11 e A12 e
N 1 N 1 N
0 0 0 ... 0 0 A21 e A22 e A11 e
1 1
B11 B12 0 0 ... 0 0 0
1 1 2 2
B21 B
22 B 11 B
12 0 ... 0 0 0
2 2 3 3
0 B21 B22 B11 B12 ... ... ... ...
0 0 ... ... ... ... ... 0
M
... ... ... ... ... ... ... ...
... ... ... ... ... ... 0 0
N 2 N 2 N 1 N 1
0 0 0 ... B21 e B22 e B11 e B12 e 0
Ne 1 Ne 1 Ne N
0 0 ... 0 B 21 B 22 B 11 B12 e
1.1.9 Algorithm for assembling the linear system
Connectivity matrix cl , j , where l 1, 2,..., N E and j 1, 2 .
cl ,1 l is the global label for the first node of lth element
cl ,2 l 1 is the global label for the second node of lth element
Handout: Algorithm 1.1.1
1.1.10 Thomas algorithm for tridiagonal systems
Handout: Algorithm 1.1.2
XI
�N N linear system T x r , where matrix T has the tridiagonal form
a1 b1
c 2 a 2 b2
c3 a3 b3
cN 1 aN 1 bN 1
cN aN
Thomas algorithm proceeds in two stages. In the first stage, the tridiagonal
system is reduced to the bidiagonal system B x y involving the bidiagonal
coefficient matrix
1 d1
0 1 d2
0 1 d3
0 1 dN 1
0 1
In the second stage, bidiagonal system is solved by back substitution.
1.1.11 Finite element code
To economize the computer memory, we store the diagonal, super-diagonal and
sub-diagonal elements of the global diffusion matrix in three vectors,
ait Di ,i , bit Di ,i 1 , cit Di 1,i
Handout: compact algorithm
Sample program:
XII
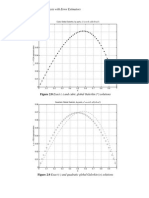
� x2
Source term: s x s0 exp 5 , where s0 is constant.
L2
XIII