0% found this document useful (0 votes)
108 views13 pagesGenerator Load, KW, Torque, Speed Relation
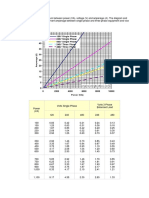
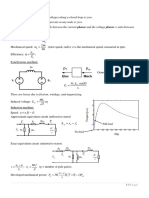
The document provides formulas for calculating power output from generators, including three-phase and single-phase systems, and explains the relationship between load, current, voltage, and power factor. It details how an Automatic Voltage Regulator (AVR) maintains voltage stability during load changes and describes the mechanical torque required from the engine as electrical load increases. Additionally, it emphasizes the importance of maintaining high power factor and the quick response of the AVR to prevent voltage instability in shipboard electrical systems.
Uploaded by
Min TheimCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as DOCX, PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
108 views13 pagesGenerator Load, KW, Torque, Speed Relation
The document provides formulas for calculating power output from generators, including three-phase and single-phase systems, and explains the relationship between load, current, voltage, and power factor. It details how an Automatic Voltage Regulator (AVR) maintains voltage stability during load changes and describes the mechanical torque required from the engine as electrical load increases. Additionally, it emphasizes the importance of maintaining high power factor and the quick response of the AVR to prevent voltage instability in shipboard electrical systems.
Uploaded by
Min TheimCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as DOCX, PDF, TXT or read online on Scribd
/ 13