0% found this document useful (0 votes)
46 views19 pagesSVM Using Iris Dataset by Hyparlink
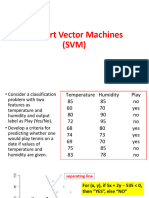
Support Vector Machine (SVM) is a supervised machine learning algorithm primarily used for classification, aiming to create the best decision boundary (hyper-plane) to separate classes in n-dimensional space. There are two types of SVM: Linear SVM for linearly separable data and Non-linear SVM for non-linearly separable data, which employs kernel methods to transform data into higher dimensions. SVM has advantages such as effectiveness in high-dimensional spaces and memory efficiency, but it may struggle with large datasets and noisy data.
Uploaded by
seemukgdeepCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as DOCX, PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
46 views19 pagesSVM Using Iris Dataset by Hyparlink
Support Vector Machine (SVM) is a supervised machine learning algorithm primarily used for classification, aiming to create the best decision boundary (hyper-plane) to separate classes in n-dimensional space. There are two types of SVM: Linear SVM for linearly separable data and Non-linear SVM for non-linearly separable data, which employs kernel methods to transform data into higher dimensions. SVM has advantages such as effectiveness in high-dimensional spaces and memory efficiency, but it may struggle with large datasets and noisy data.
Uploaded by
seemukgdeepCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as DOCX, PDF, TXT or read online on Scribd
/ 19