0% found this document useful (0 votes)
9 views30 pages02 Linear Time-Invariant Systems
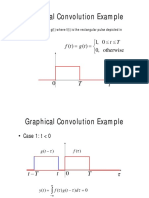
Chapter 02 discusses Linear Time-Invariant (LTI) Systems, highlighting their linearity and time-invariance properties, which allow for detailed analysis and modeling of various physical processes. It explains the convolution sum and integral as essential tools for understanding the response of LTI systems to inputs, emphasizing the significance of impulse responses. Additionally, the chapter covers properties of LTI systems, including commutativity, distributivity, and stability, along with practice problems to reinforce the concepts.
Uploaded by
akhan.bee22seecsCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
0% found this document useful (0 votes)
9 views30 pages02 Linear Time-Invariant Systems
Chapter 02 discusses Linear Time-Invariant (LTI) Systems, highlighting their linearity and time-invariance properties, which allow for detailed analysis and modeling of various physical processes. It explains the convolution sum and integral as essential tools for understanding the response of LTI systems to inputs, emphasizing the significance of impulse responses. Additionally, the chapter covers properties of LTI systems, including commutativity, distributivity, and stability, along with practice problems to reinforce the concepts.
Uploaded by
akhan.bee22seecsCopyright
© © All Rights Reserved
We take content rights seriously. If you suspect this is your content, claim it here.
Available Formats
Download as PDF, TXT or read online on Scribd
/ 30