02-alignment.pdf

Lecture 2
Sequence Alignment
Burr Settles
IBS Summer Research Program 2008
bsettles@cs.wisc.edu
www.cs.wisc.edu/~bsettles/ibs08/

Sequence Alignment:
Task Definition
• given:
– a pair of sequences (DNA or protein)
– a method for scoring a candidate alignment
• do:
– determine the correspondences between substrings in
the sequences such that the similarity score is
maximized

Why Do Alignment?
• homology: similarity due to descent from a common
ancestor
• often we can infer homology from similarity
• thus we can sometimes infer structure/function from
sequence similarity

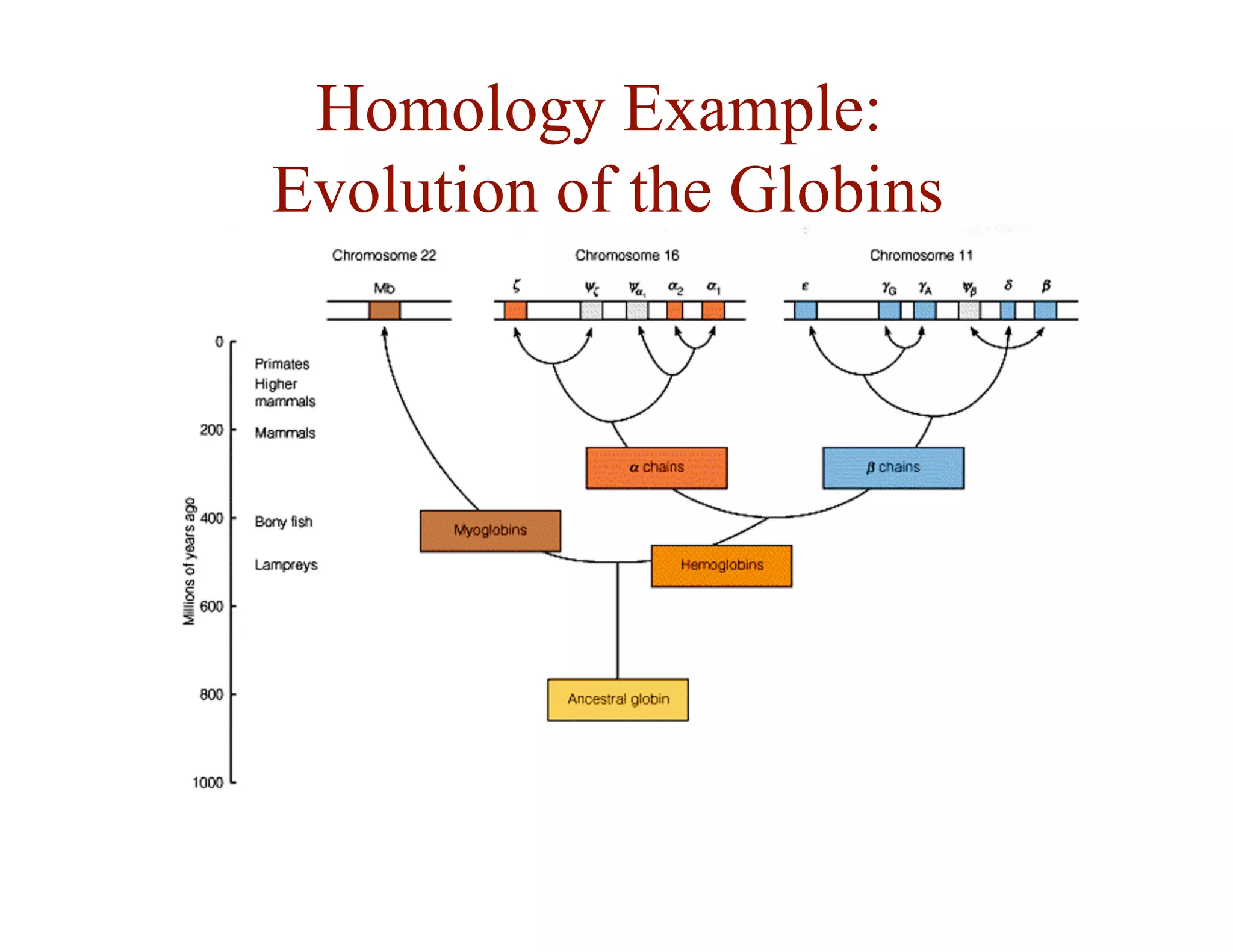
Homology Example:
Evolution of the Globins

Homology
• homologous sequences can be divided into two groups
– orthologous sequences: sequences that differ because
they are found in different species (e.g. human α
-globin and mouse α-globin)
– paralogous sequences: sequences that differ because of
a gene duplication event (e.g. human α-globin and
human β-globin, various versions of both )

Issues in Sequence Alignment
• the sequences we’re comparing probably differ in length
• there may be only a relatively small region in the
sequences that match
• we want to allow partial matches (i.e. some amino acid
pairs are more substitutable than others)
• variable length regions may have been inserted/deleted
from the common ancestral sequence

Sequence Variations
• sequences may have diverged from a common ancestor
through various types of mutations:
– substitutions (ACGA AGGA)
– insertions (ACGA ACCGGAGA)
– deletions (ACGGAGA AGA)
• the latter two will result in gaps in alignments

Insertions, Deletions and
Protein Structure
loop structures: insertions/deletions
here not so significant
• Why is it that two “similar” sequences may have large
insertions/deletions?
– some insertions and deletions may not significantly
affect the structure of a protein

Example Alignment: Globins
• figure at right shows prototypical
structure of globins
• figure below shows part of alignment
for 8 globins (-’s indicate gaps)

Three Key Questions
• Q1: what do we want to align?
• Q2: how do we “score” an alignment?
• Q3: how do we find the “best” alignment?

Q1: What Do We Want to Align?
• global alignment: find best match of both sequences in
their entirety
• local alignment: find best subsequence match
• semi-global alignment: find best match without penalizing
gaps on the ends of the alignment

The Space of Global Alignments
• some possible global alignments for ELV and VIS
ELV
VIS
-ELV
VIS-
--ELV
VIS--
ELV-
-VIS
ELV--
--VIS
E-LV
VIS-
EL-V
-VIS

Q2: How Do We Score
Alignments?
• gap penalty function
– w(k) indicates cost of a gap of length k
• substitution matrix
– s(a,b) indicates score of aligning character a with
character b

Linear Gap Penalty Function
• different gap penalty functions require somewhat different
dynamic programming algorithms
• the simplest case is when a linear gap function is used
€
w(k) = g× k
where g is a constant
• we’ll start by considering this case

Scoring an Alignment
• the score of an alignment is the sum of the scores for pairs of
aligned characters plus the scores for gaps
• example: given the following alignment
VAHV---D--DMPNALSALSDLHAHKL
AIQLQVTGVVVTDATLKNLGSVHVSKG
• we would score it by
s(V,A) + s(A,I) + s(H,Q) + s(V,L) + 3g + s(D,G) + 2g …

Q3: How Do We Find the Best
Alignment?
• simple approach: compute & score all possible alignments
• but there are
n
n
n
n
n n
π
2
2
2
)
!
(
)!
2
(
2
≈
=








possible global alignments for 2 sequences of length n
• e.g. two sequences of length 100 have possible
alignments
77
10
≈

Pairwise Alignment Via
Dynamic Programming
• dynamic programming: solve an instance of a
problem by taking advantage of solutions for
subparts of the problem
– reduce problem of best alignment of two sequences to
best alignment of all prefixes of the sequences
– avoid recalculating the scores already considered
• example: Fibonacci sequence 1, 1, 2, 3, 5, 8, 13, 21, 34…
• first used in alignment by Needleman & Wunsch,
Journal of Molecular Biology, 1970

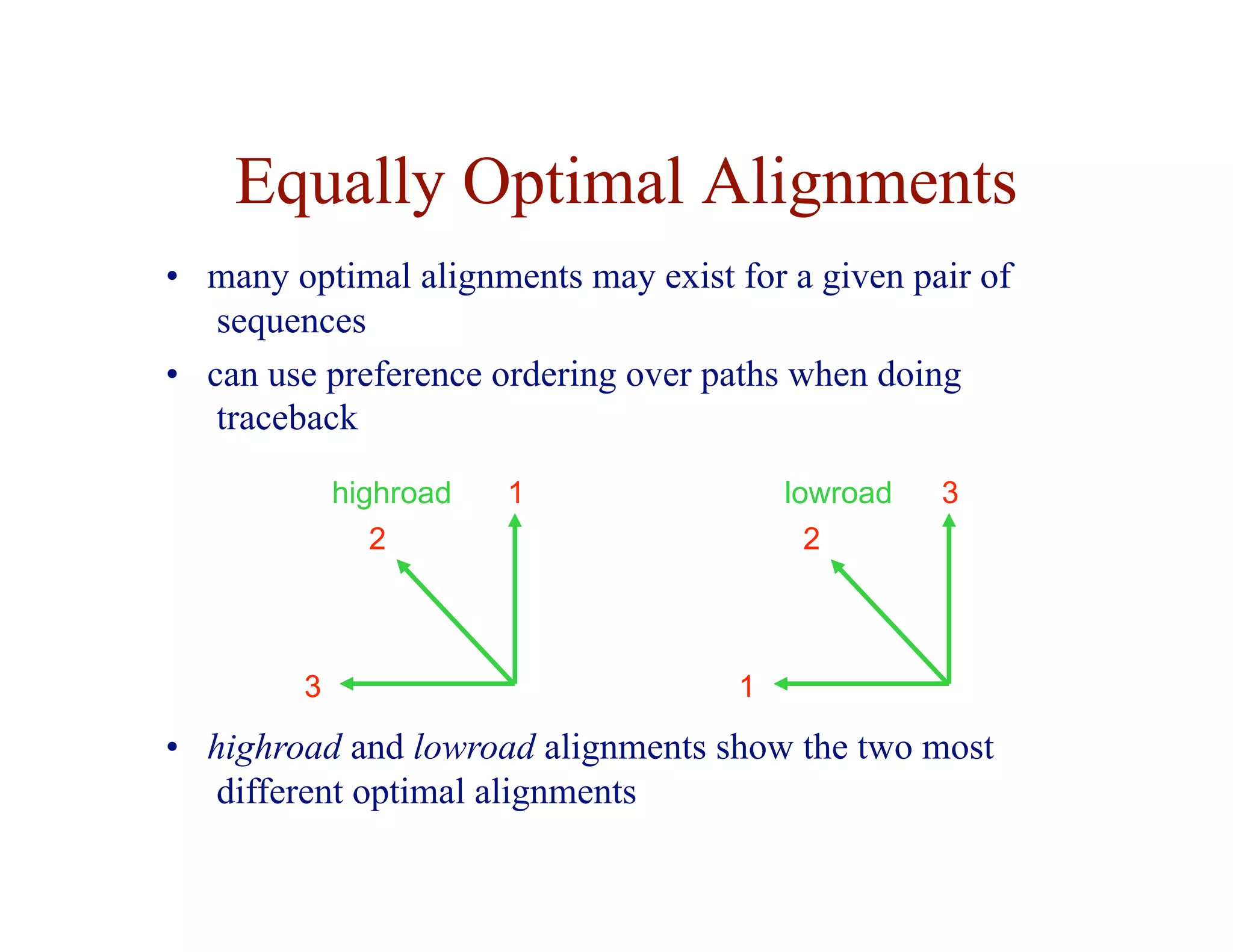
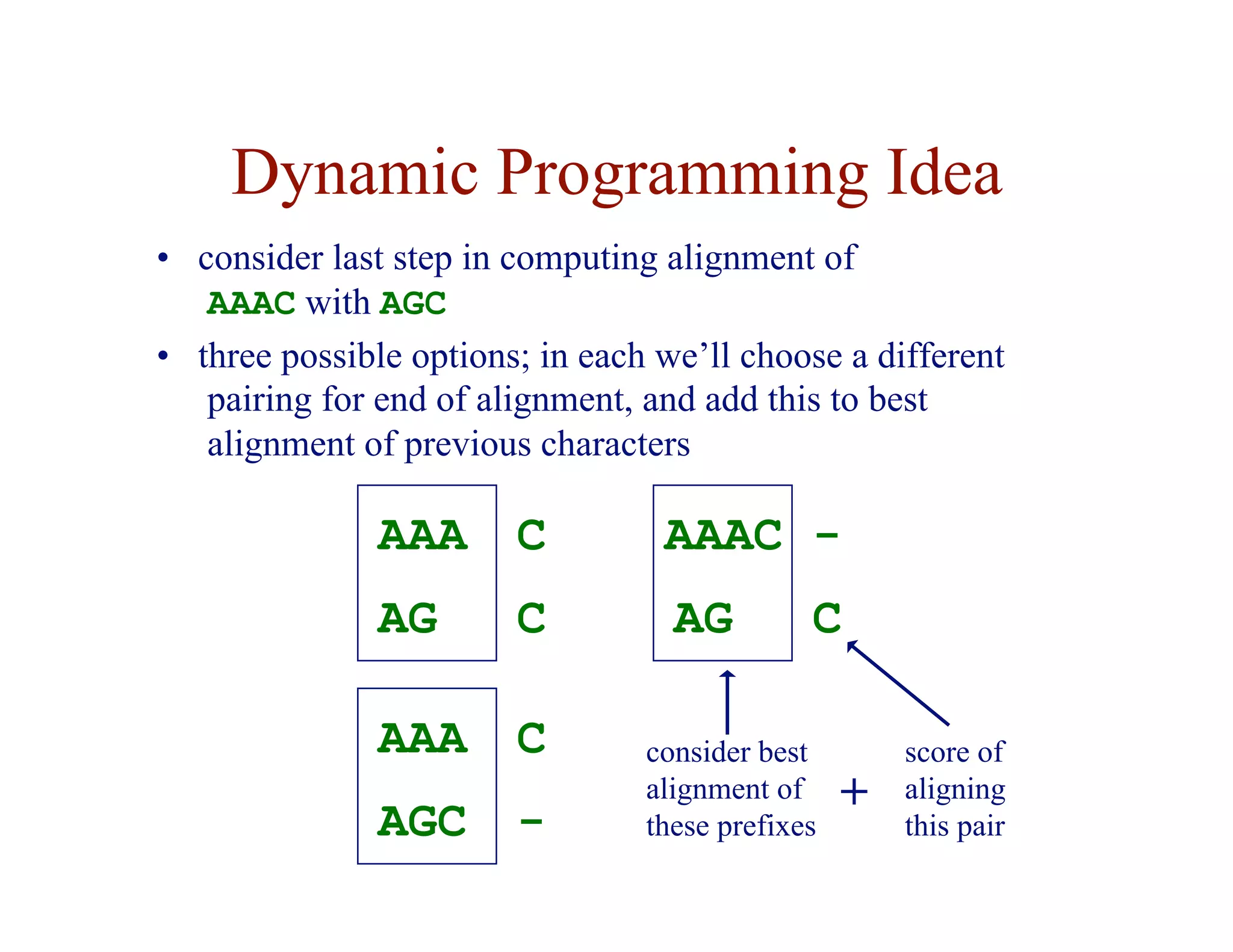
Dynamic Programming Idea
• consider last step in computing alignment of
AAAC with AGC
• three possible options; in each we’ll choose a different
pairing for end of alignment, and add this to best
alignment of previous characters
AAA
C
AG
C AAAC
C
AG
-
AAA
-
AGC
C consider best
alignment of
these prefixes
score of
aligning
this pair
+

Dynamic Programming Idea
• given an n-character sequence x, and an m-character
sequence y
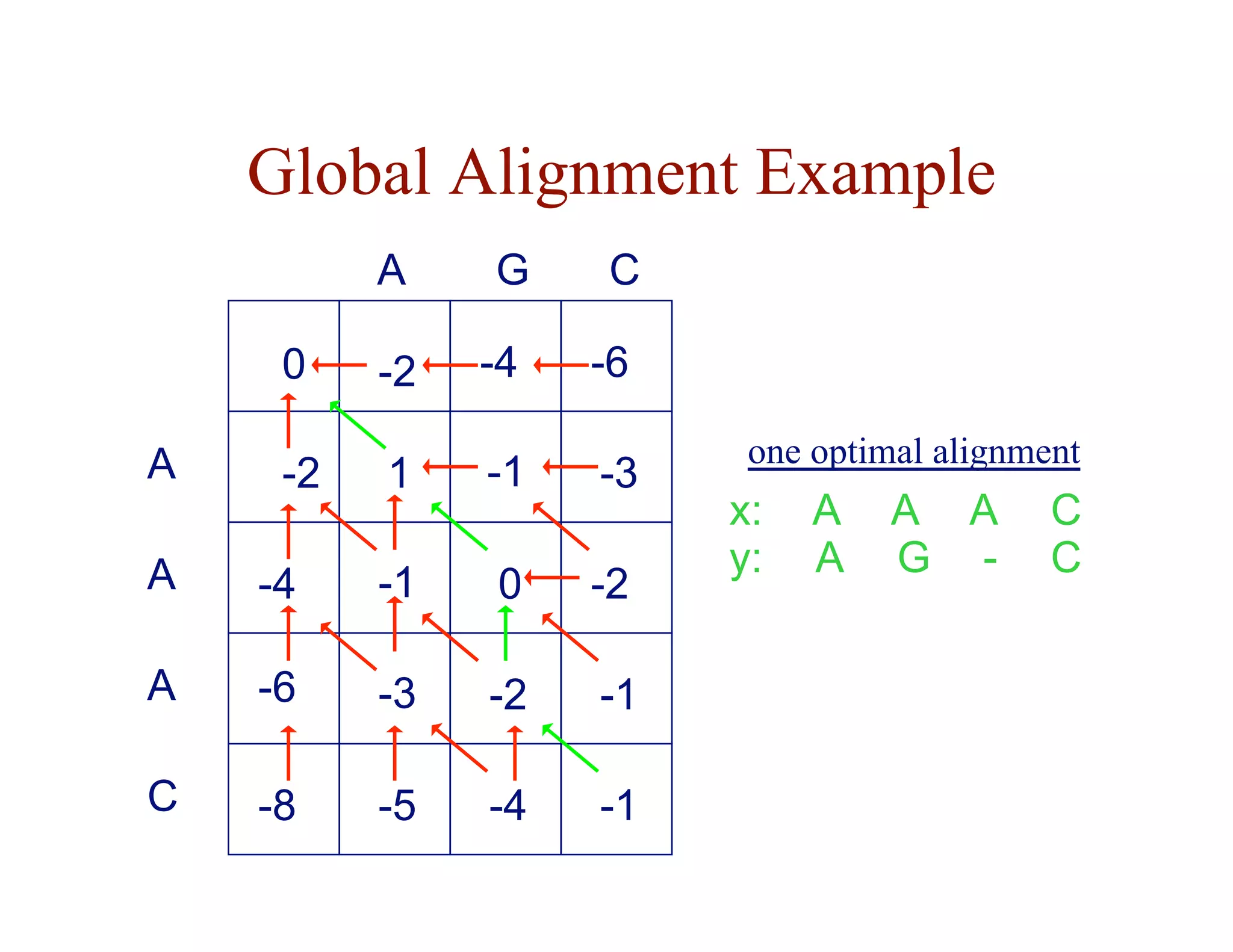
• construct an (n+1) × (m+1) matrix F
• F ( i, j ) = score of the best alignment of
x[1…i ] with y[1…j ]
A
A
C
A G
A
C
score of best alignment of
AAA to AG

Needleman-Wunch Algorithm
• one way to specify the DP is in terms of its recurrence
relation:





+
−
+
−
+
−
−
=
g
j
i
F
g
j
i
F
y
x
s
j
i
F
j
i
F
j
i
)
1
,
(
)
,
1
(
)
,
(
)
1
,
1
(
max
)
,
(
match xi with yj
insertion in x
insertion in y

DP Algorithm Sketch:
Global Alignment
• initialize first row and column of matrix
• fill in rest of matrix from top to bottom, left to right
• for each F ( i, j ), save pointer(s) to cell(s) that resulted in
best score
• F (m, n) holds the optimal alignment score; trace pointers
back from F (m, n) to F (0, 0) to recover alignment

Initializing Matrix
A g
A 2g
C
A G
A 3g
C 4g
0 3g
g 2g

Global Alignment Example
• suppose we choose the following scoring scheme:
+1
-1
g (penalty for aligning with a gap) = -2
=
)
,
( i
i y
x
s
i
i y
x =
when
i
i y
x ≠
when

A
A
C
A G
A
C
+1
-1
g = -2
=
)
,
( i
i y
x
s
i
i y
x =
when
i
i y
x ≠
when

A -2
A -4
C
A G
A -6
C -8
0 -6
-2 -4
1 -1 -3
-1 0 -2
-3 -2 -1
-5 -4 -1
x:
y:
A
-
A
G
A
A
C
C
one optimal alignment

Equally Optimal Alignments
• many optimal alignments may exist for a given pair of
sequences
• can use preference ordering over paths when doing
traceback
highroad lowroad
1
2
3 1
2
3
• highroad and lowroad alignments show the two most
different optimal alignments

Highroad & Lowroad Alignments
A -2
A -4
C
A G
A -6
C -8
0 -6
-2 -4
1 -1 -3
-1 0 -2
-3 -2 -1
-5 -4 -1
x:
y:
A
G
A
A
A
-
C
C
lowroad alignment
x:
y:
A
-
A
G
A
A
C
C
highroad alignment

DP Comments
• works for either DNA or protein sequences, although the
substitution matrices used differ
• finds an optimal alignment
• the exact algorithm (and computational complexity)
depends on gap penalty function (we’ll come back to this)

Local Alignment
• so far we have discussed global alignment, where we are
looking for best match between sequences from one end to
the other
• more commonly, we will want a local alignment, the best
match between subsequences of x and y

Local Alignment Motivation
• useful for comparing protein sequences that share a
common motif (conserved pattern) or domain
(independently folded unit) but differ elsewhere
• useful for comparing DNA sequences that share a similar
motif but differ elsewhere
• useful for comparing protein sequences against genomic
DNA sequences (long stretches of uncharacterized
sequence)
• more sensitive when comparing highly diverged sequences

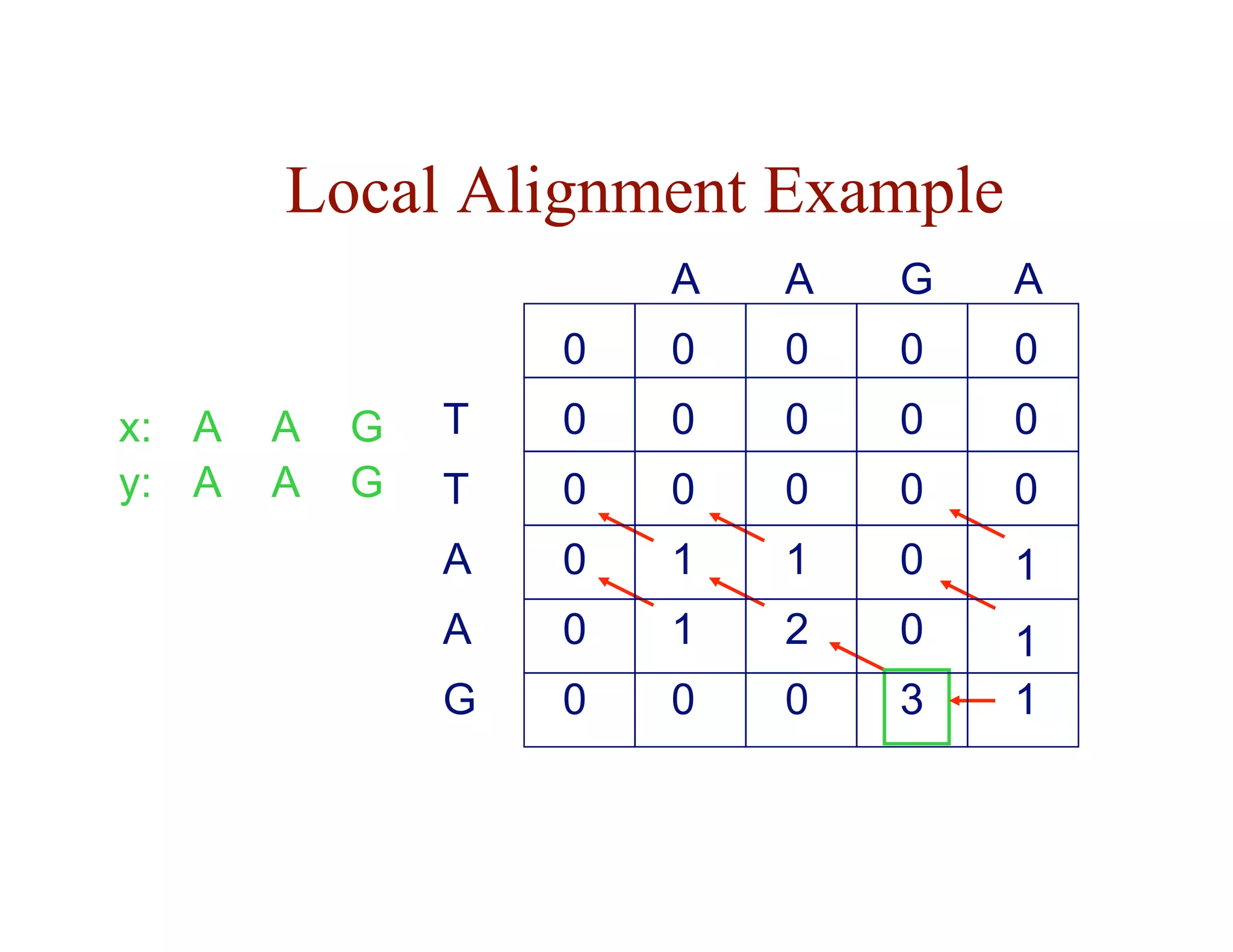
Local Alignment DP Algorithm
• original formulation: Smith & Waterman, Journal of
Molecular Biology, 1981
• interpretation of array values is somewhat different
– F ( i, j ) = score of the best alignment of a suffix of
x[1…i ] and a suffix of y[1…j ]








+
−
+
−
+
−
−
=
0
)
1
,
(
)
,
1
(
)
,
(
)
1
,
1
(
max
)
,
(
g
j
i
F
g
j
i
F
y
x
s
j
i
F
j
i
F
j
i
• the recurrence relation is slightly different than for global
algorithm

• initialization: first row and first column initialized with 0’s
• traceback:
– find maximum value of F(i, j); can be anywhere in
matrix
– stop when we get to a cell with value 0

Local Alignment Example
T
T
A
A
G
G
A A
A
+1
-1
g = -2
=
)
,
( i
i y
x
s
i
i y
x =
when
i
i y
x ≠
when

Local Alignment Example
0
0
0
0 0
0
0
0 0
0
0
T
T
A
A
G
0
0
0
0
0
0 0
G
0
A
0
A
0
A
1
0
1
1 2
3
1
1
1
x:
y:
G
G
A
A
A
A

More On Gap Penalty Functions
• a gap of length k is more probable than k gaps of length 1
– a gap may be due to a single mutational event that
inserted/deleted a stretch of characters
– separated gaps are probably due to distinct mutational
events
• a linear gap penalty function treats these cases the same
• it is more common to use an affine gap penalty function,
which involves two terms:
– a penalty h associated with opening a gap
– a smaller penalty g for extending the gap

Gap Penalty Functions
• linear



=
≥
+
=
0
,
0
1
,
)
(
k
k
gk
h
k
w
gk
k
w =
)
(
• affine

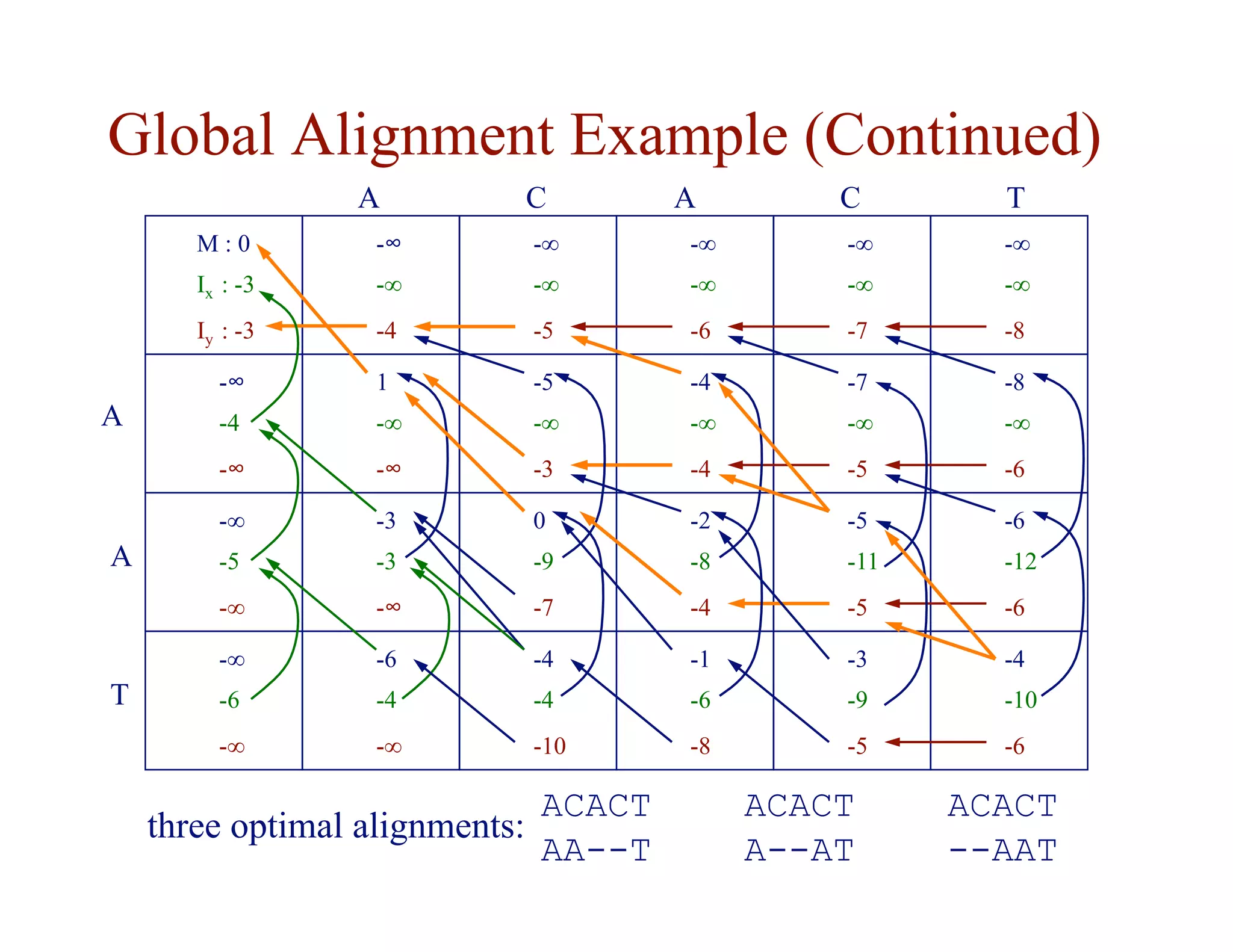
Dynamic Programming for the
Affine Gap Penalty Case
• to do in time, need 3 matrices instead of 1
)
,
( j
i
M
)
,
( j
i
Ix
)
,
( j
i
Iy
best score given that y[j] is
aligned to a gap
best score given that x[i] is
aligned to a gap
best score given that x[i] is
aligned to y[j]
)
( 2
n
O

Global Alignment DP for the





+
−
−
+
−
−
+
−
−
=
)
,
(
)
1
,
1
(
)
,
(
)
1
,
1
(
)
,
(
)
1
,
1
(
max
)
,
(
j
i
y
j
i
x
j
i
y
x
s
j
i
I
y
x
s
j
i
I
y
x
s
j
i
M
j
i
M



+
−
+
+
−
=
g
j
i
I
g
h
j
i
M
j
i
I
x
x
)
,
1
(
)
,
1
(
max
)
,
(



+
−
+
+
−
=
g
j
i
I
g
h
j
i
M
j
i
I
y
y
)
1
,
(
)
1
,
(
max
)
,
(
match xi with yj
insertion in x
insertion in y
open gap in x
extend gap in x
open gap in y
extend gap in y

Global Alignment DP for the
−∞
=
×
+
=
×
+
=
=
column
leftmost
and
row
in top
cells
other
)
,
0
(
)
0
,
(
0
)
0
,
0
(
j
g
h
j
I
i
g
h
i
I
M
y
x
• initialization
• traceback
– start at largest of
– stop at any of
– note that pointers may traverse all three
matrices
)
,
(
),
,
(
),
,
( n
m
I
n
m
I
n
m
M y
x
)
0
,
0
(
),
0
,
0
(
),
0
,
0
( y
x I
I
M

(Affine Gap Penalty)
M : 0
Ix : -3
Iy : -3
-∞
-∞
-4
-∞
-∞
-5
-∞
-∞
-7
-∞
-∞
-6
-∞
-∞
-8
1
-∞
-∞
-5
-∞
-3
-7
-∞
-5
-4
-∞
-4
-8
-∞
-6
-∞
-4
-∞
-3
-3
-∞
0
-9
-7
-5
-11
-5
-2
-8
-4
-6
-12
-6
-∞
-5
-∞
-6
-4
-∞
-4
-4
-10
-3
-9
-5
-1
-6
-8
-4
-10
-6
-∞
-6
-∞
A C A C T
A
A
T
h = -3, g = -1

Global Alignment Example (Continued)
M : 0
Ix : -3
Iy : -3
-∞
-∞
-4
-∞
-∞
-5
-∞
-∞
-7
-∞
-∞
-6
-∞
-∞
-8
1
-∞
-∞
-5
-∞
-3
-7
-∞
-5
-4
-∞
-4
-8
-∞
-6
-∞
-4
-∞
-3
-3
-∞
0
-9
-7
-5
-11
-5
-2
-8
-4
-6
-12
-6
-∞
-5
-∞
-6
-4
-∞
-4
-4
-10
-3
-9
-5
-1
-6
-8
-4
-10
-6
-∞
-6
-∞
A C A C T
A
A
T
ACACT
--AAT
ACACT
A--AT
ACACT
AA--T
three optimal alignments:

Local Alignment DP for the







+
−
−
+
−
−
+
−
−
=
0
)
,
(
)
1
,
1
(
)
,
(
)
1
,
1
(
)
,
(
)
1
,
1
(
max
)
,
(
j
i
y
j
i
x
j
i
y
x
s
j
i
I
y
x
s
j
i
I
y
x
s
j
i
M
j
i
M



+
−
+
+
−
=
g
j
i
I
g
h
j
i
M
j
i
I
x
x
)
,
1
(
)
,
1
(
max
)
,
(



+
−
+
+
−
=
g
j
i
I
g
h
j
i
M
j
i
I
y
y
)
1
,
(
)
1
,
(
max
)
,
(

Local Alignment DP for the
−∞
=
=
=
=
,
of
column
leftmost
and
row
in top
cells
0
)
,
0
(
0
)
0
,
(
0
)
0
,
0
(
y
x I
I
j
M
i
M
M
• initialization
• traceback
– start at largest
– stop at
)
,
( j
i
M
0
)
,
( =
j
i
M

Gap Penalty Functions



=
≥
+
=
0
,
0
1
,
)
(
k
k
gk
h
k
w
gk
k
w =
)
(
)
log(
)
( k
g
h
k
w ×
+
=
• linear:
• affine:
• concave: a function for which the following holds for all
k, l, m ≥ 0
e.g.
)
(
)
(
)
(
)
( k
w
l
k
w
m
k
w
l
m
k
w −
+
≤
+
−
+
+

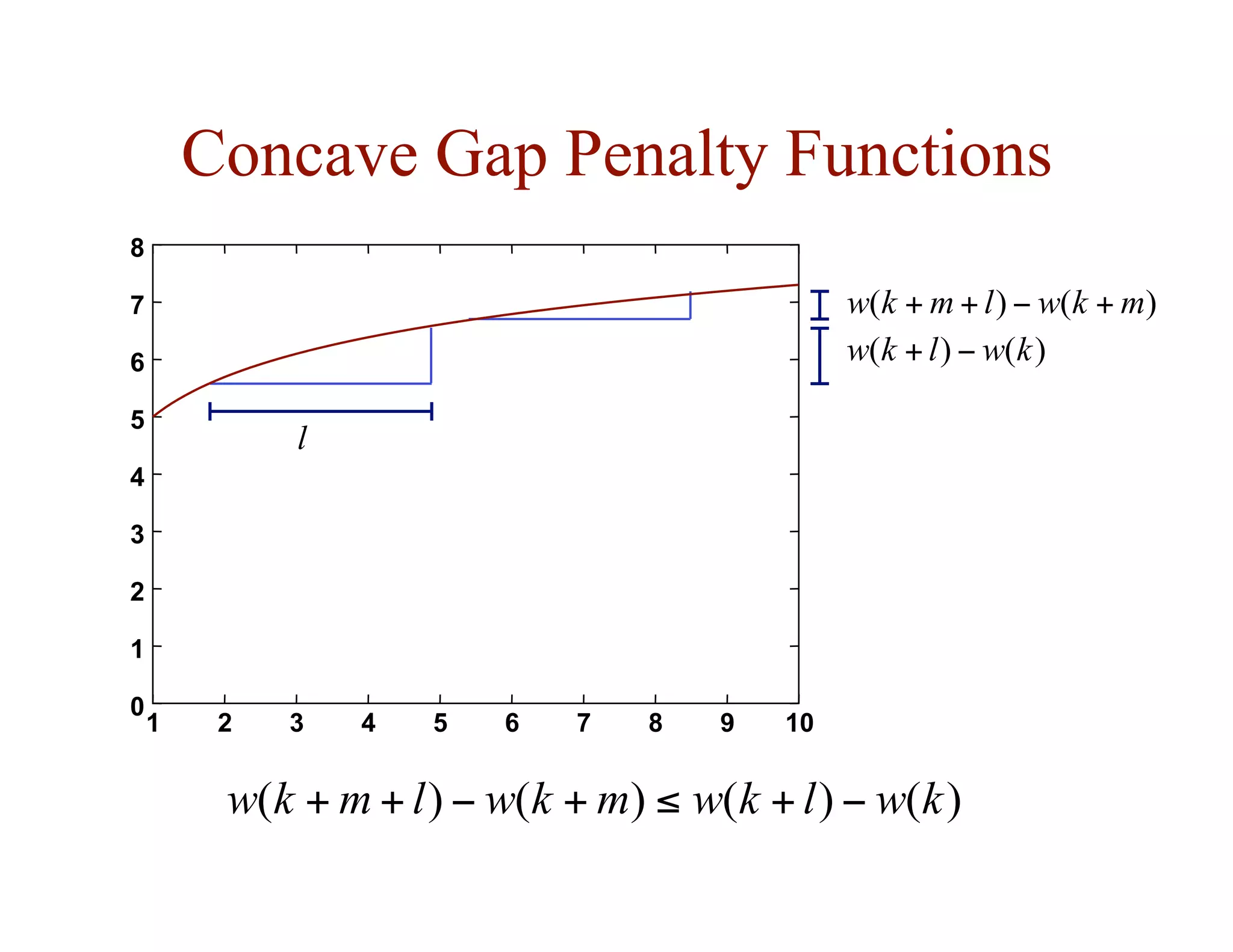
Concave Gap Penalty Functions
( ) ( )
w k m l w k m
+ + − +
0
1
2
3
4
5
6
7
8
1 2 3 4 5 6 7 8 9 10
( ) ( )
w k l w k
+ −
)
(
)
(
)
(
)
( k
w
l
k
w
m
k
w
l
m
k
w −
+
≤
+
−
+
+
l

More On Scoring Matches
• so far, we’ve discussed multiple gap penalty functions, but
only one match-scoring scheme:
+1
-1
=
)
,
( i
i y
x
s
i
i y
x =
when
i
i y
x ≠
when
• for protein sequence alignment, some amino acids have
similar structures and can be substituted in nature:
aspartic acid (D) glutamic acid (E)

Substitution Matrices
• two popular sets of matrices for protein sequences
– PAM matrices [Dayhoff et al., 1978]
– BLOSUM matrices [Henikoff & Henikoff, 1992]
• both try to capture the the relative substitutability of amino
acid pairs in the context of evolution

Heuristic Methods
• the algorithms we learned today take O(nm) time to align
sequences, which is too slow for searching large databases
– imagine an internet search engine, but where queries and results
are protein sequences
• heuristic methods do fast approximation to dynamic
programming
– example: BLAST [Altschul et al., 1990; Altschul et al., 1997]
– break sequence into small (e.g. 3 base pair) “words”
– scan database for word matches
– extend all matches to seek high-scoring alignments
– tradeoff: sensitivity for speed

Multiple Sequence Alignment
• we’ve only discussed
aligning 2 sequences, but
we may want to do more
• discover common motifs in
a set of sequences
(e.g. DNA sequences that
bind the same protein)
• characterize a set of
sequences
(e.g. a protein family)
• much more complex
Figure from A. Krogh, An Introduction to Hidden Markov Models for Biological Sequences

Next Time…
• basic molecular biology
• sequence alignment
• probabilistic sequence models
• gene expression analysis
• protein structure prediction
– by Ameet Soni

02-alignment.pdf

More Related Content

Similar to 02-alignment.pdf

Recently uploaded

02-alignment.pdf