16_Greedy_Algorithms Greedy_AlgorithmsGreedy_Algorithms

Introduction to Algorithms
Chapter 16: Greedy Algorithms

Greedy Algorithms
 Similar to dynamic programming, but simpler approach
 Also used for optimization problems
 Idea: When we have a choice to make, make the one
that looks best right now
 Make a locally optimal choice in hope of getting a globally optimal
solution
 Greedy algorithms don’t always yield an optimal solution
 Makes the choice that looks best at the moment in order
to get optimal solution.

Fractional Knapsack Problem
 Knapsack capacity: W
 There are n items: the i-th item has value vi and weight
wi
 Goal:
 find xi such that for all 0  xi  1, i = 1, 2, .., n
 wixi  W and
 xivi is maximum

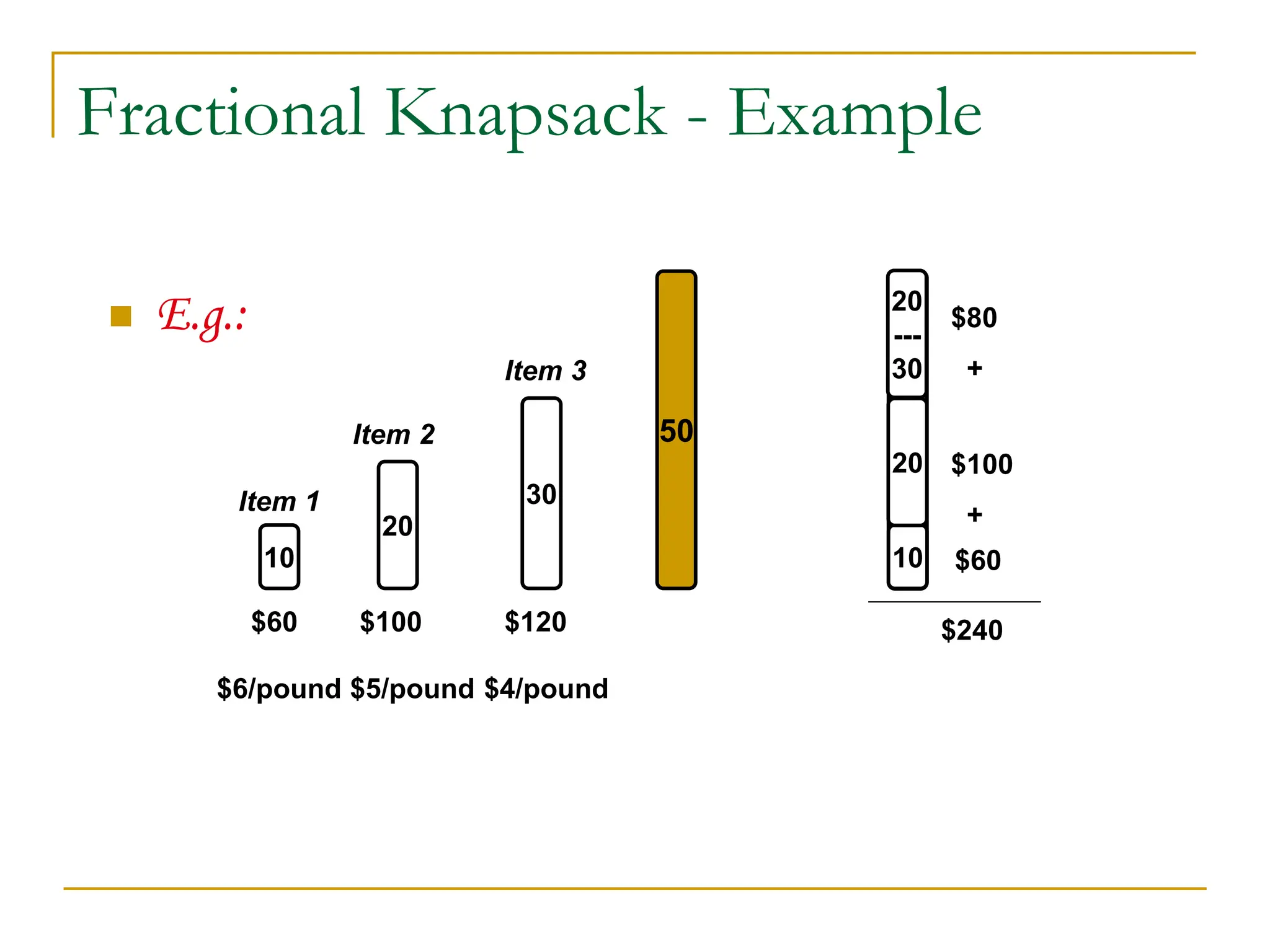
50
Fractional Knapsack - Example
 E.g.:
10
20
30
50
Item 1
Item 2
Item 3
$60 $100 $120
10
20
$60
$100
+
$240
$6/pound $5/pound $4/pound
20
---
30
$80
+

 Greedy strategy 1:
 Pick the item with the maximum value
 E.g.:
 W = 1
 w1 = 100, v1 = 2
 w2 = 1, v2 = 1
 Taking from the item with the maximum value:
Total value taken = v1/w1 = 2/100
 Smaller than what the thief can take if choosing the
other item
Total value (choose item 2) = v2/w2 = 1

Greedy strategy 2:
 Pick the item with the maximum value per pound vi/wi
 If the supply of that element is exhausted and the thief can
carry more: take as much as possible from the item with the
next greatest value per pound
 It is good to order items based on their value per pound
n
n
w
v
w
v
w
v


 ...
2
2
1
1

Alg.: Fractional-Knapsack (W, v[n], w[n])
1. While w > 0 and as long as there are items remaining
2. pick item with maximum vi/wi
3. xi  min (1, w/wi)
4. remove item i from list
5. w  w – xiwi
 w – the amount of space remaining in the knapsack (w = W)
 Running time: (n) if items already ordered; else (nlgn)

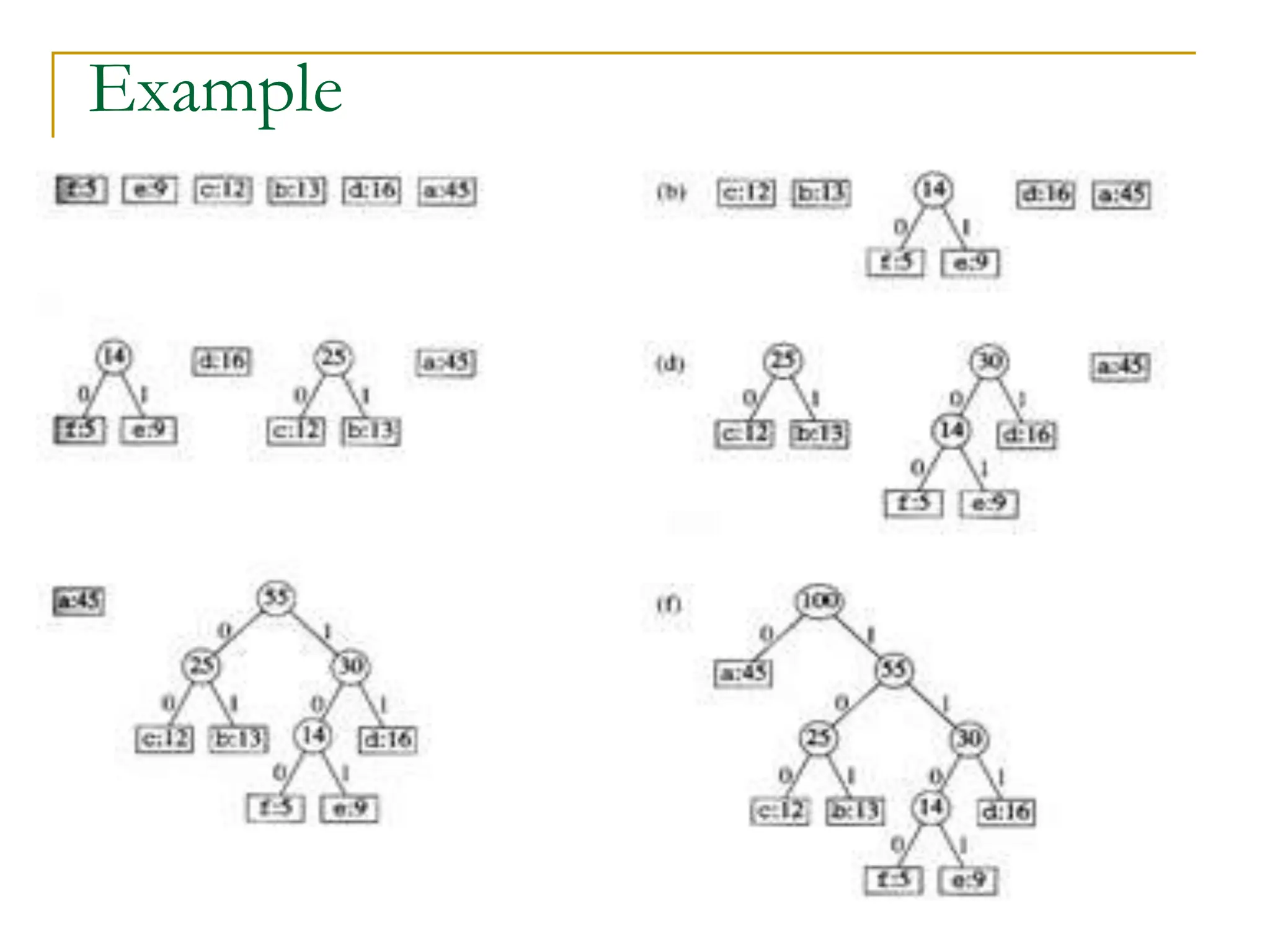
Huffman Code Problem
 Huffman’s algorithm achieves data
compression by finding the best variable
length binary encoding scheme for the
symbols that occur in the file to be
compressed.

 The more frequent a symbol occurs, the
shorter should be the Huffman binary word
representing it.
 The Huffman code is a prefix-free code.
 No prefix of a code word is equal to another
codeword.

Overview
 Huffman codes: compressing data (savings of 20% to
90%)
 Huffman’s greedy algorithm uses a table of the
frequencies of occurrence of each character to build
up an optimal way of representing each character as
a binary string
C: Alphabet

Example
 Assume we are given a data file that contains only 6 symbols,
namely a, b, c, d, e, f With the following frequency table:
 Find a variable length prefix-free encoding scheme that
compresses this data file as much as possible?

 Left tree represents a fixed length encoding scheme
 Right tree represents a Huffman encoding scheme

Constructing A Huffman Code
O(lg n)
O(lg n)
O(lg n)
Total computation time = O(n lg n)
// C is a set of n characters
// Q is implemented as a binary min-heap O(n)

Cost of a Tree T
 For each character c in the alphabet C
 let f(c) be the frequency of c in the file
 let dT(c) be the depth of c in the tree
 It is also the length of the codeword. Why?
 Let B(T) be the number of bits required to
encode the file (called the cost of T)
B(T )  f (c)dT (c)
cC


In the pseudocode that follows:
 we assume that C is a set of n characters and that
each character c €C is an object with a defined
frequency f [c].
 The algorithm builds the tree T corresponding to the
optimal code
 A min-priority queue Q, is used to identify the two
least-frequent objects to merge together.
 The result of the merger of two objects is a new
object whose frequency is the sum of the
frequencies of the two objects that were merged.

Running time of Huffman's algorithm
 The running time of Huffman's algorithm assumes
that Q is implemented as a binary min-heap.
 For a set C of n characters, the initialization of Q in
line 2 can be performed in O(n) time using the
BUILD-MINHEAP
 The for loop in lines 3-8 is executed exactly n - 1
times, and since each heap operation requires
time O(lg n), the loop contributes O(n lg n) to the
running time. Thus, the total running time of
HUFFMAN on a set of n characters is O(n lg n).

Prefix Code
 Prefix(-free) code: no codeword is also a prefix of some other
codewords (Un-ambiguous)
 An optimal data compression achievable by a character code can
always be achieved with a prefix code
 Simplify the encoding (compression) and decoding
 Encoding: abc  0 . 101. 100 = 0101100
 Decoding: 001011101 = 0. 0. 101. 1101  aabe
 Use binary tree to represent prefix codes for easy decoding
 An optimal code is always represented by a full binary tree, in which
every non-leaf node has two children
 |C| leaves and |C|-1 internal nodes Cost:


C
c
T c
d
c
f
T
B )
(
)
(
)
(
Frequency of c
Depth of c (length of the codeword)

Huffman Code
 Reduce size of data by 20%-90% in general
 If no characters occur more frequently than others,
then no advantage over ASCII
 Encoding:
 Given the characters and their frequencies, perform the
algorithm and generate a code. Write the characters
using the code
 Decoding:
 Given the Huffman tree, figure out what each character
is (possible because of prefix property)

Application on Huffman code
 Both the .mp3 and .jpg file formats use
Huffman coding at one stage of the
compression

Dynamic Programming vs. Greedy Algorithms
 Dynamic programming
 We make a choice at each step
 The choice depends on solutions to subproblems
 Bottom up solution, from smaller to larger subproblems
 Greedy algorithm
 Make the greedy choice and THEN
 Solve the subproblem arising after the choice is made
 The choice we make may depend on previous choices,
but not on solutions to subproblems
 Top down solution, problems decrease in size

16_Greedy_Algorithms Greedy_AlgorithmsGreedy_Algorithms

More Related Content

Similar to 16_Greedy_Algorithms Greedy_AlgorithmsGreedy_Algorithms

More from Shanmuganathan C

Recently uploaded

16_Greedy_Algorithms Greedy_AlgorithmsGreedy_Algorithms