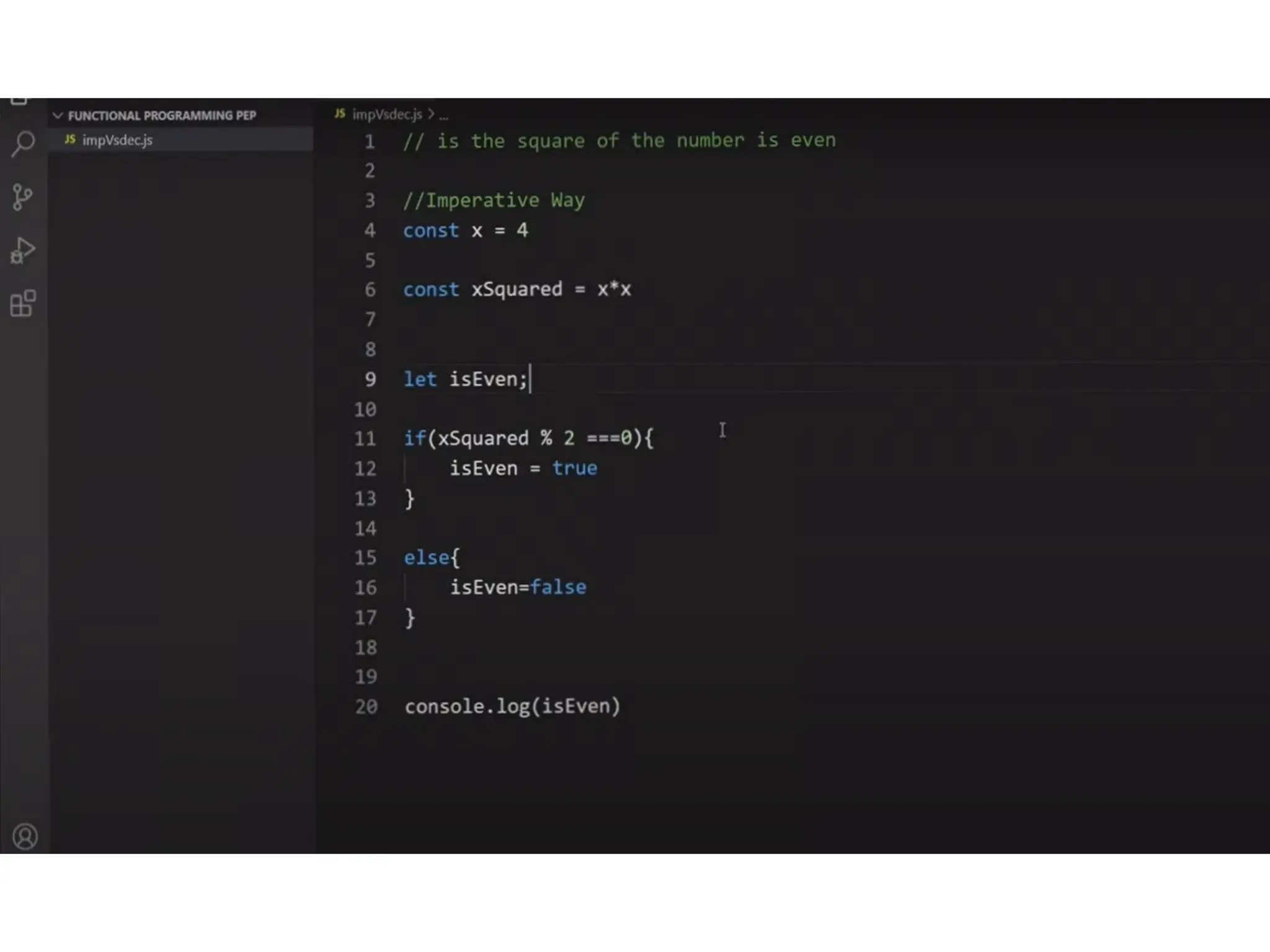
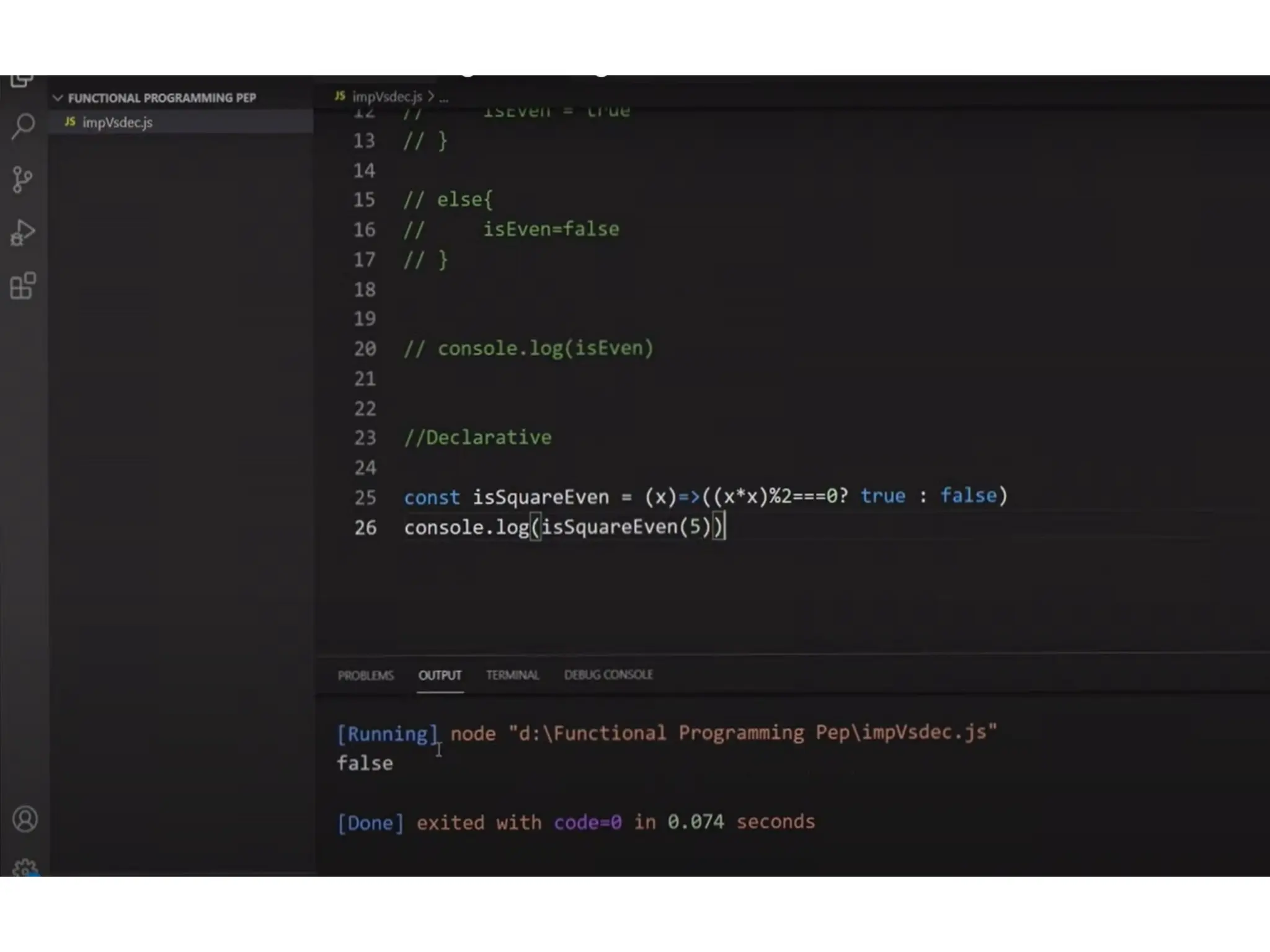
8. Functional Programming_updated(1).pptx

A higher order function (HOF) is a function that follows at least one of the
following conditions −
•Takes on or more functions as argument
•Returns a function as its result
Properties of the Higher-Order Function
The properties of the Higher-Order Function are as shown below:
1.The function will work as an instance of the object type.
2.In the Higher-Order Function, we can easily store the function in the form of
the variable.
3.In the Higher-Order Function, a function can contain another function as a
parameter.
4.In the higher-order function, a function can also return the function.
5.We can store these functions in the data structure in the hash table, lists etc.

Lazy evaluation is an evaluation strategy which holds the evaluation of an
expression until its value is needed. It avoids repeated evaluation. Haskell is a
good example of such a functional programming language whose fundamentals
are based on Lazy Evaluation.
Lazy evaluation is used in Unix map functions to improve their performance by
loading only required pages from the disk. No memory will be allocated for the
remaining pages.
Lazy Evaluation Advantages
−
• It allows the language runtime to discard sub-expressions that are not directly
linked to the final result of the expression.
• It reduces the time complexity of an algorithm by discarding the temporary
computations and conditionals.
• It allows the programmer to access components of data structures out-of-
order after initializing them, as long as they are free from any circular
dependencies.
• It is best suited for loading data which will be infrequently accessed.
Lazy Evaluation Drawbacks
−
• It forces the language runtime to hold the evaluation of sub-expressions until it
is required in the final result by creating thunks (delayed objects).
• Sometimes it increases space complexity of an algorithm.
• It is very difficult to find its performance because it contains thunks of
expressions before their execution.

PARADIGMS AND COMPUTER
PROGRAMMING
FUNDAMENTALS
Subject Code - ITC305 SE
IT SEM III

Module III
Declarative Programming
Paradigm: Functional
Programming

Declarative Programming Paradigm:
Functional Programming
Topics to be covered in this module: (Total Hrs: 7)
• Introduction to Lambda Calculus (1 Hr)
• Functional Programming Concepts, (2 Hrs)
• Evaluation order, Higher order functions, (2 Hrs)
• I/O- Streams (1 Hr)
• Monads (1 Hr)
Text Book :
1. Graham Hutton, Programming in Haskell, 2nd Edition, Cambridge
University Press 2016.
http://www.cs.nott.ac.uk/~pszgmh/pih.html#contents
2. Scott M L, Programming Language Pragmatics, 3rd Edn., Morgan
Kaufmann Publishers, 2009 [Chapter 10]
Other References: –
https://downloads.haskell.org/~ghc/7.8.4/docs/html/users_guide/

Functional programming
• Functional programming languages are
specially designed to handle symbolic
computation and list processing applications.
Functional programming is based on
mathematical functions. Some of the popular
functional programming languages include:
Lisp, Python, Erlang, Haskell, Clojure, etc.

Types of Functional Progamming
• Pure Functional Languages − These types of
functional languages support only the
functional paradigms. For example − Haskell.
• Impure Functional Languages − These types
of functional languages support the functional
paradigms and imperative style programming.
For example − LISP.

Functional Programming – Characteristics
• Functional programming languages are designed on the concept
of mathematical functions that use conditional expressions and
recursion to perform computation.
• Functional programming supports higher-order functions and
lazy evaluation features.
• Functional programming languages don’t support flow Controls
like loop statements and conditional statements like If-Else and
Switch Statements. They directly use the functions and
functional calls.
• Like OOP, functional programming languages support popular
concepts such as Abstraction, Encapsulation, Inheritance, and
Polymorphism.

Functional Programming – Advantages
• Bugs-Free Code − Functional programming does not support state, so
there are no side-effect results and we can write error-free codes.
• Efficient Parallel Programming − Functional programming languages
have NO Mutable state, so there are no state-change issues. One can
program "Functions" to work parallel as "instructions". Such codes
support easy reusability and testability.
• Efficiency − Functional programs consist of independent units that
can run concurrently. As a result, such programs are more efficient.
• Supports Nested Functions − Functional programming supports
Nested Functions.
• Lazy Evaluation − Functional programming supports Lazy Functional
Constructs like Lazy Lists, Lazy Maps, etc.

Functional Programming – Disadvantage
• Functional programming requires a large
memory space. As it does not have state, you
need to create new objects every time to
perform actions.

Functional Programming vs. Object-oriented
Programming
Functional Programming OOP
Uses Immutable data. Uses Mutable data.
Follows Declarative Programming Model. Follows Imperative Programming Model.
Focus is on: “What you are doing” Focus is on “How you are doing”
Supports Parallel Programming Not suitable for Parallel Programming
Its functions have no-side effects Its methods can produce serious side effects.
Flow Control is done using function calls &
function calls with recursion
Flow control is done using loops and
conditional statements.
It uses "Recursion" concept to iterate
Collection Data.
It uses "Loop" concept to iterate Collection
Data. For example: For-each loop in Java
Execution order of statements is not so
important.
Execution order of statements is very
important.
Supports both "Abstraction over Data" and
"Abstraction over Behavior". Supports only "Abstraction over Data".

Lambda calculus
• Lambda calculus is a framework developed by Alonzo
Church in 1930s to study computations with functions.
• Function creation − Church introduced the
notation λx.E to denote a function in which ‘x’ is a formal
argument and ‘E’ is the functional body. These functions
can be of without names and single arguments.
• Function application − Church used the notation E1.E2 to
denote the application of function E1 to actual
argument E2. And all the functions are on single
argument.

Syntax of Lambda Calculus
• Lamdba calculus includes three different types
of expressions, i.e.,
• E :: = x(variables)
• | E1 E2(function application)
• | λx.E(function creation)
• Where λx.E is called Lambda abstraction and E
is known as λ-expressions.

Evaluating Lambda Calculus
• Pure lambda calculus has no built-in functions. Let us evaluate
the following expression −
• (+ (* 5 6) (* 8 3)) Here, we can’t start with '+' because it only
operates on numbers. There are two reducible expressions:
• (* 5 6) and (* 8 3).
• We can reduce either one first. For example −
(+ (* 5 6) (* 8 3))
(+ 30 (* 8 3))
(+ 30 24)
= 54

Scope, free and bound occurences
x . t
binder
body
Occurences of x in the body t are bound. Nonbound variable
occurrences are called free.
(x . y. zx(yx))x

Reduction
• Alpha Reduction
• Beta Reduction
• Eta Reduction

Alpha Reduction
Renaming of a bound variable and its bound occurrences.
x.y.y  x.z.z

Alpha Reduction
• If v and w are variables and E is a lambda
expression,
• λv . E α λw . E[v→w]
⇒
• provided that w does not occur at all in E,
which makes the substitution E[v→w] safe.

Alpha Reduction
The example substitution at the end of the
previous section contains two α-reductions:
• λy( λf . f x) y α λz . (λf . f x) z
⇒
• λz . (λf . f x) z α λz . (λg . g x) z
⇒

Beta Reduction
• If v is a variable and E and E1 are lambda
expressions,
• (λv . E) E1 β E[v→E1]
⇒
• provided that the substitution E[v→E1] is
carried out according to the rules for a safe
substitution.

Beta Reduction
• This β-reduction rule describes the function application
rule in which the actual parameter or argument E1 is
“passed to” the function (λv . E) by substituting the
argument for the formal parameter v in the function.
The left side (λv . E) E1 of a β-reduction is called a β-
redex—a term derived from the terms “reduction
expression” and meaning an expression that can be
βreduced. β-reduction serves as the main rule of
evaluation in the lambda calculus. α-reduction is simply
used to make the substitutions for variables valid.

Beta reduction: Examples
(x.y.y x)(z.u)  y.y(z.u)
(x. x x)(z.u)  (z.u) (z.u)
(y.y a)((x. x)(z.(u.u) z))  (y.y a)(z.
(u.u) z)
(y.y a)((x. x)(z.(u.u) z))  (y.y a)((x. x)
(z. z))
(y.y a)((x. x)(z.(u.u) z))  ((x. x)(z.
(u.u) z)) a

(Eta) η-reduction
• Definition: η-reduction mIf v is a variable, E is a lambda
expression (denoting a function), and v has no free occurrence in
E, λv . (E v) η E.
⇒
• Note that in the pure lambda calculus every expression is a
function, but the rule fails when E represents some constants; for
example, if 5 is a predefined constant numeral, λx . (5 x) and 5 are
not equivalent or even related. However, if E stands for a
predefined function, the rule remains valid as suggested by these
examples: λx . (sqr x) η sqr λx . (add 5 x) η (add 5). Remember,
⇒ ⇒
(add 5 x) abbreviates ((add 5) x). The requirement that x should
have no free occurrences in E is necessary to avoid a reduction
such as λx . (add x x) (add x), which is clearly invalid
⇒

(Eta) η-reduction
• However, if E stands for a predefined function, the
rule remains valid as suggested by these examples:
λx . (sqr x) η sqr
⇒
λx . (add 5 x) η (add 5).
⇒
Remember, (add 5 x) abbreviates ((add 5) x).
The requirement that x should have no free occurrences
in E is necessary to avoid a reduction such as
λx . (add x x) (add x),
⇒
which is clearly invalid.


( x y . x y) ( x . x y) ( a b . a b) NB: left assoc.
( x z . x z) ( x . x y) ( a b . a b)  conversion
( z . ( x . x y) z) ( a b . a b)  reduction
( x . x y) ( a b . a b)  reduction
( a b . a b) y  reduction
( b . y b)  reduction
y  reduction

The Church-Rosser Theorems
• If E1 ↔ E2 (are interconvertable),then there
exists an E such that E1 → E and E2 → E.
• “Reduction in any way can eventually produce
the same result.”
• If E1 → E2, and E2 is is normal form, then
there is a normal-order reduction of E1 to E2.
• “Normal-order reduction will always produce
a normal form, if one exists.”

Higher Order Functions
• A higher order function (HOF) is a function
that follows at least one of the following
conditions −
1. Takes on or more functions as argument
2. Returns a function as its result

8. Functional Programming_updated(1).pptx

8. Functional Programming_updated(1).pptx

More Related Content

Similar to 8. Functional Programming_updated(1).pptx

More from jaymalachavan

Recently uploaded

8. Functional Programming_updated(1).pptx