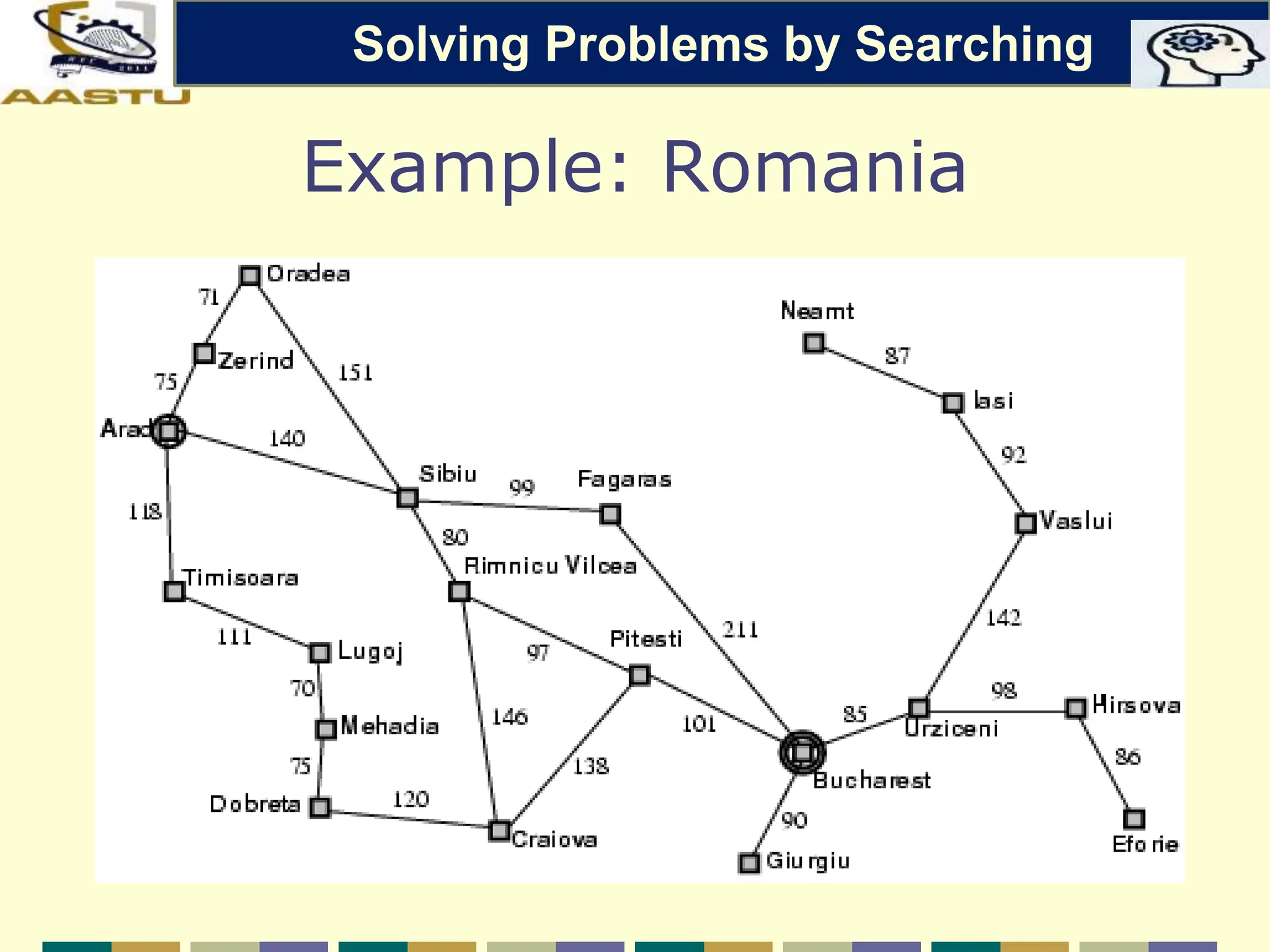
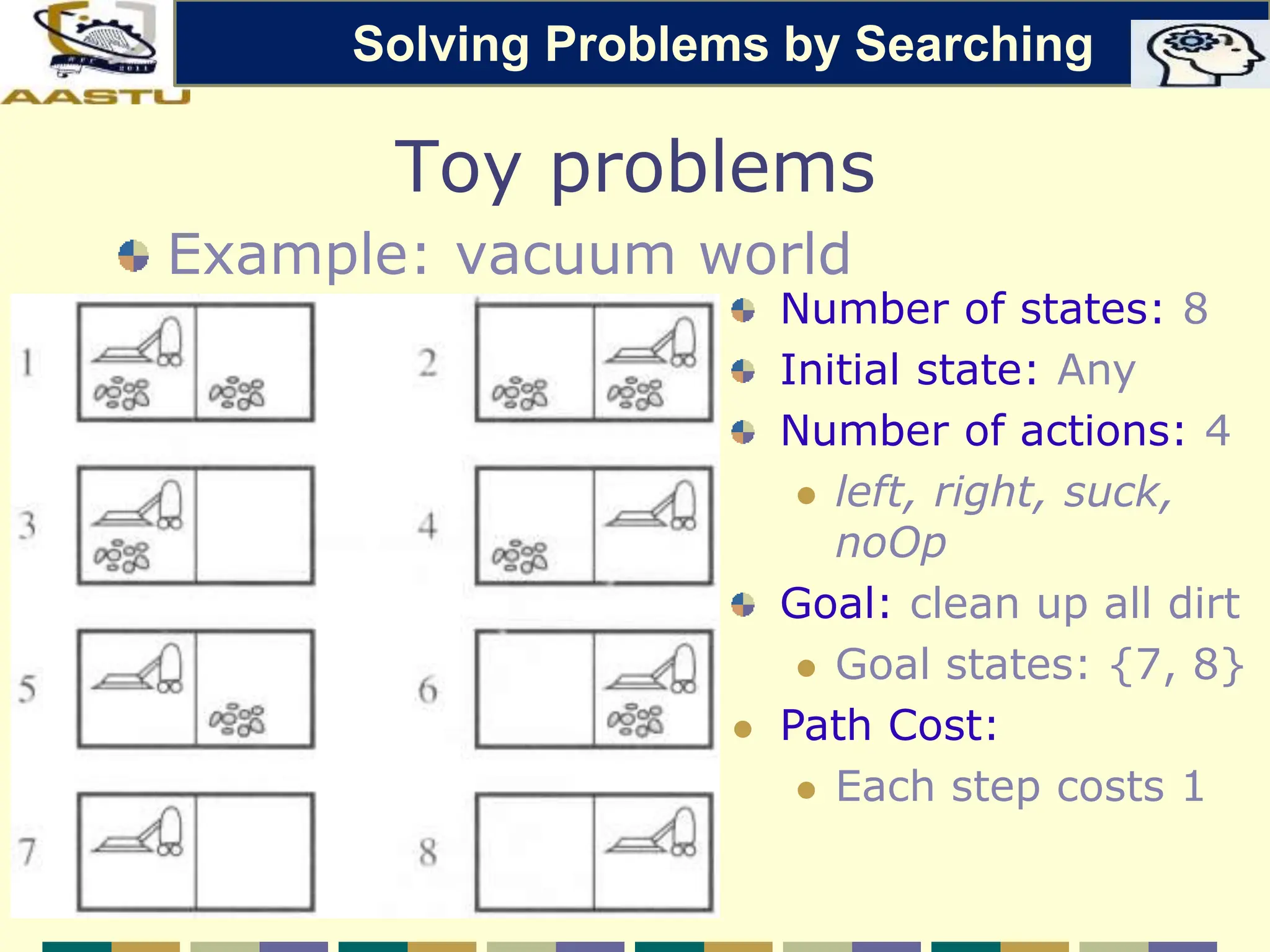
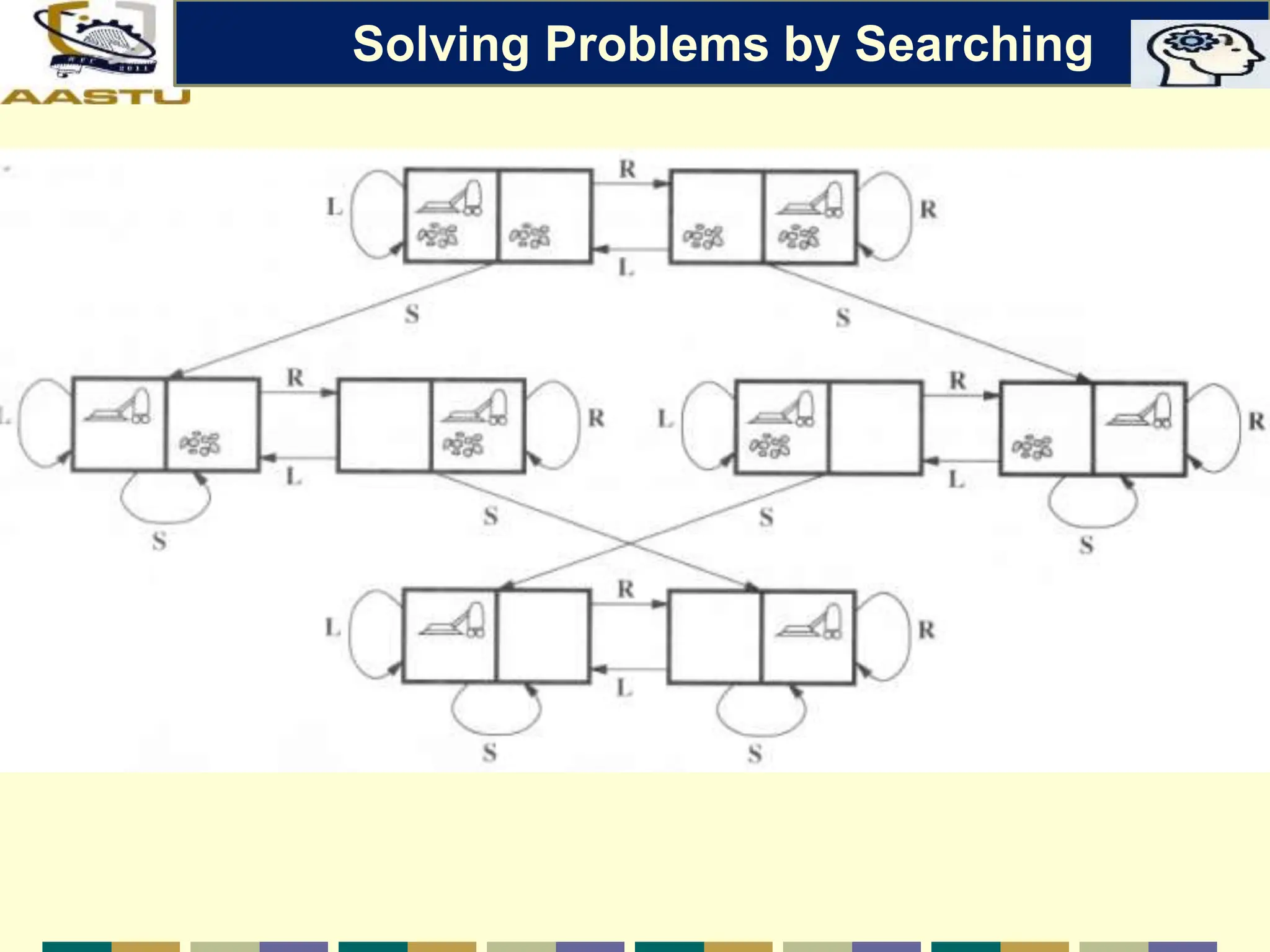
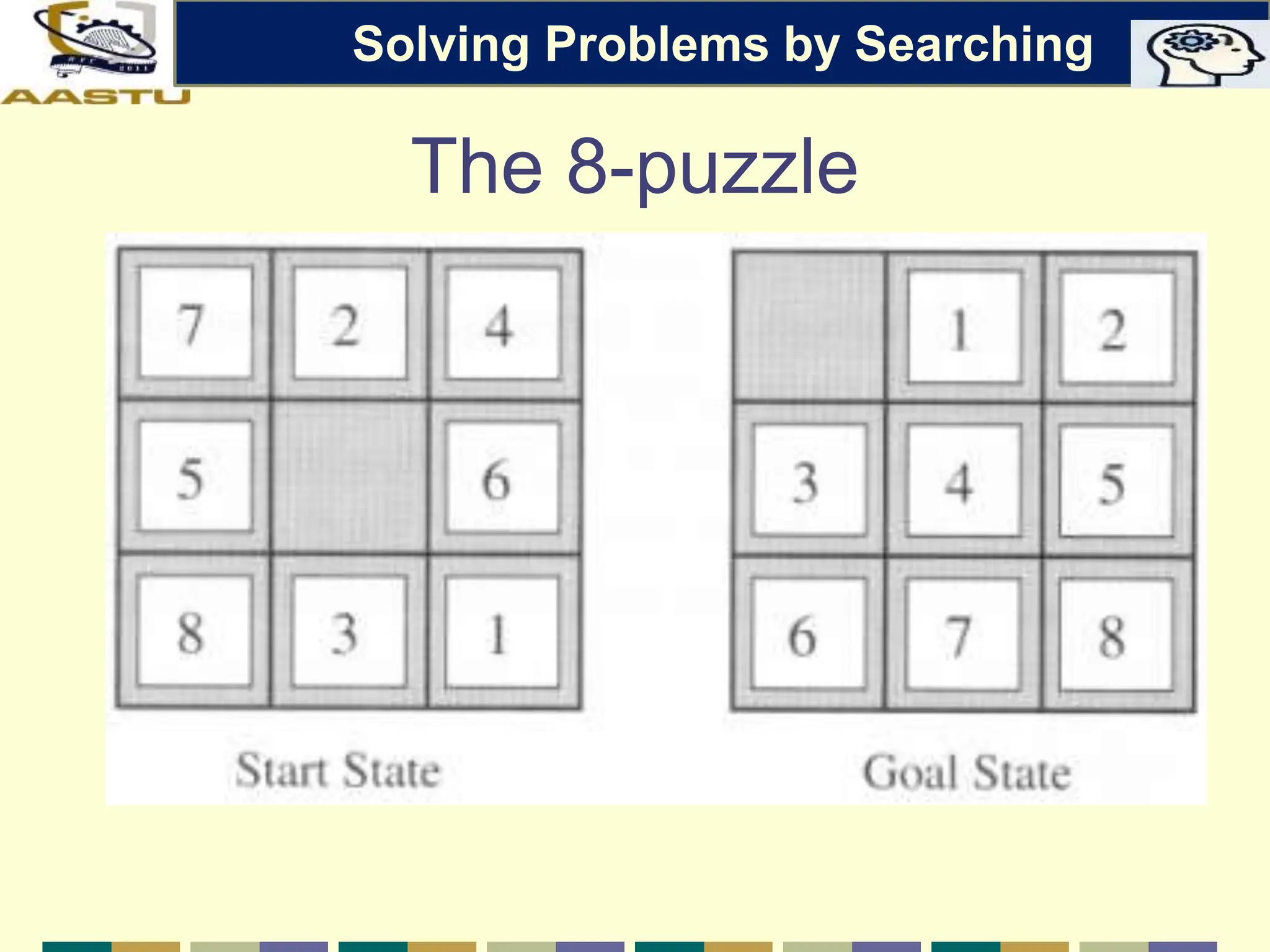
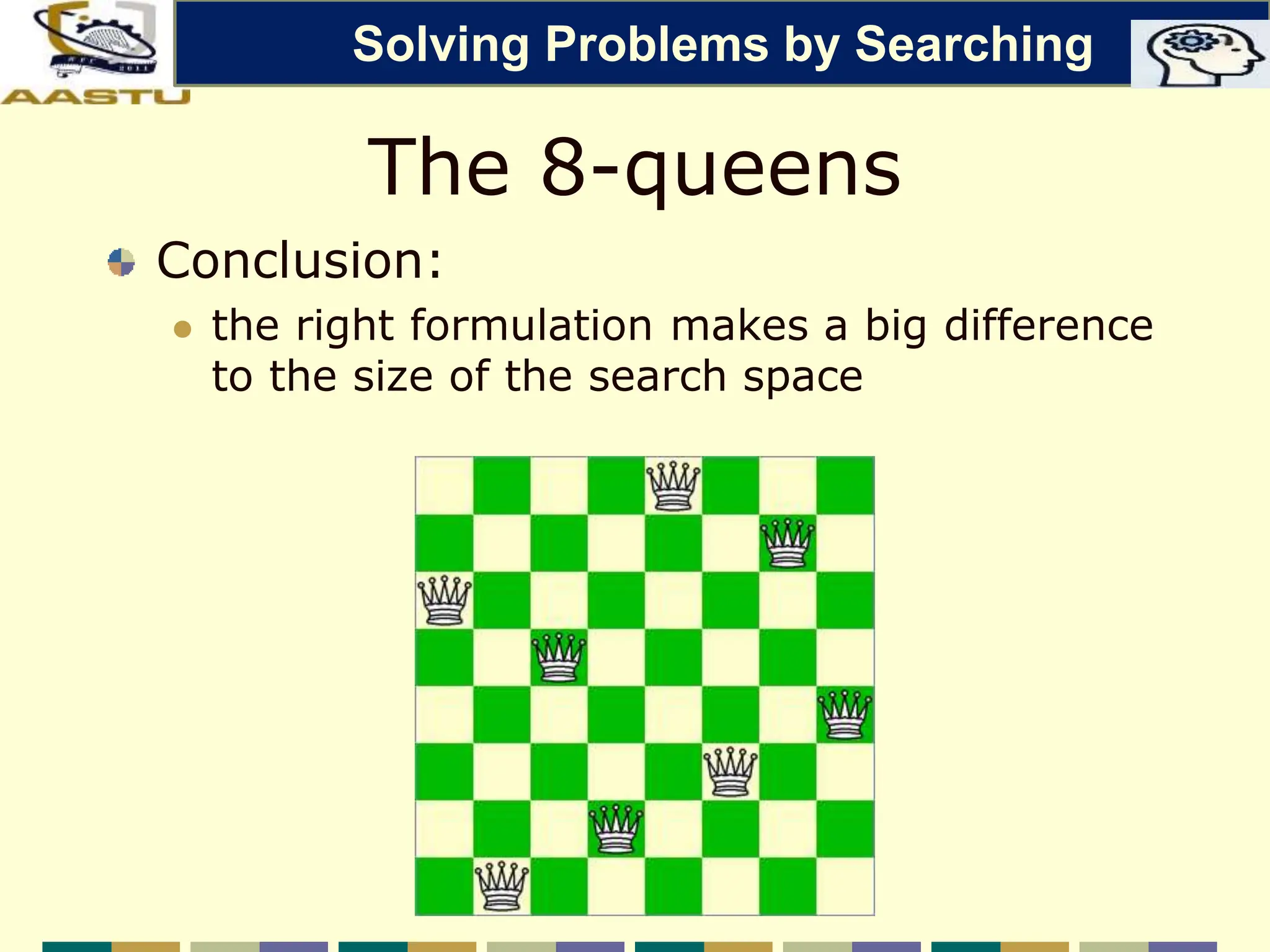
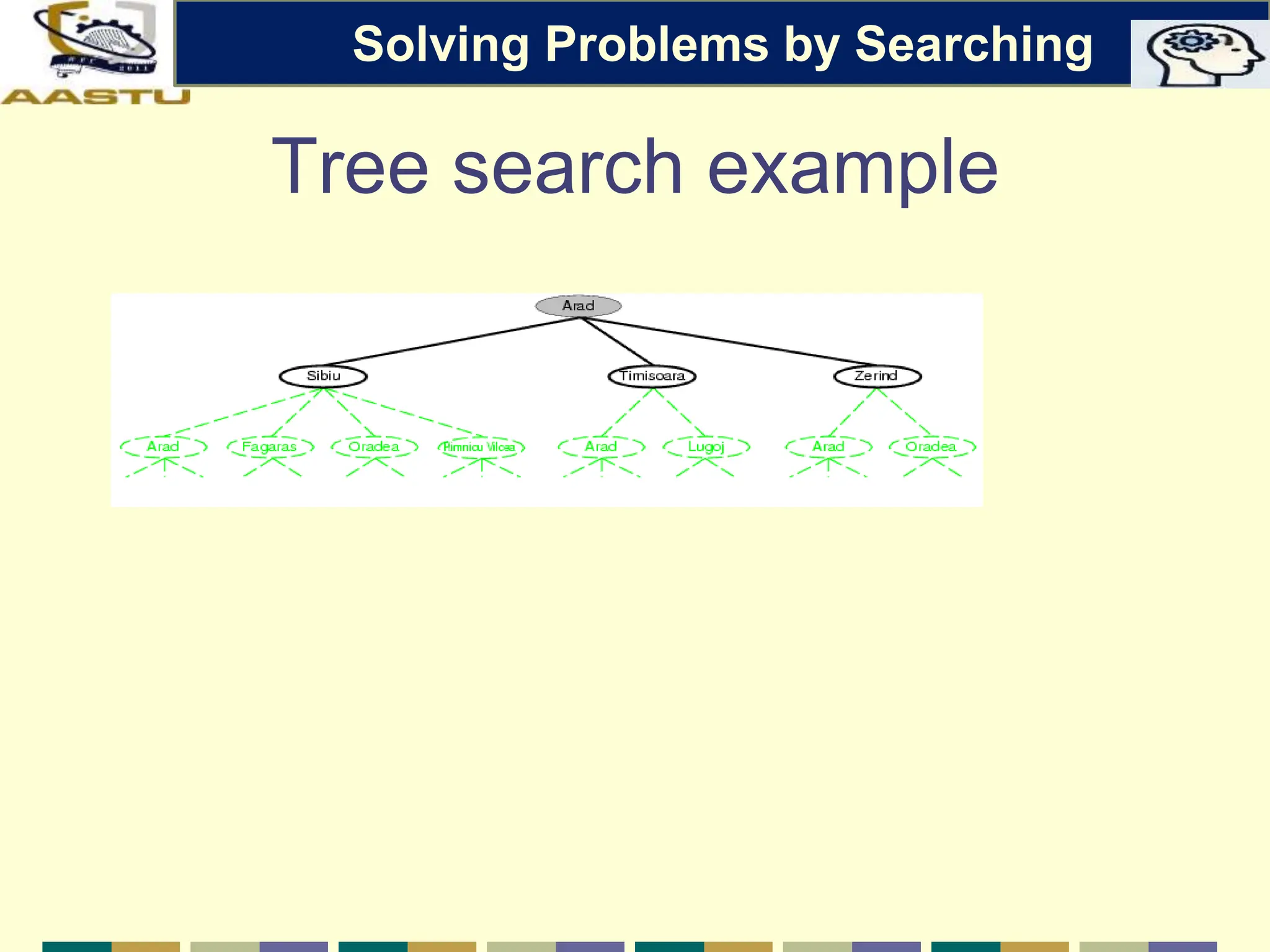
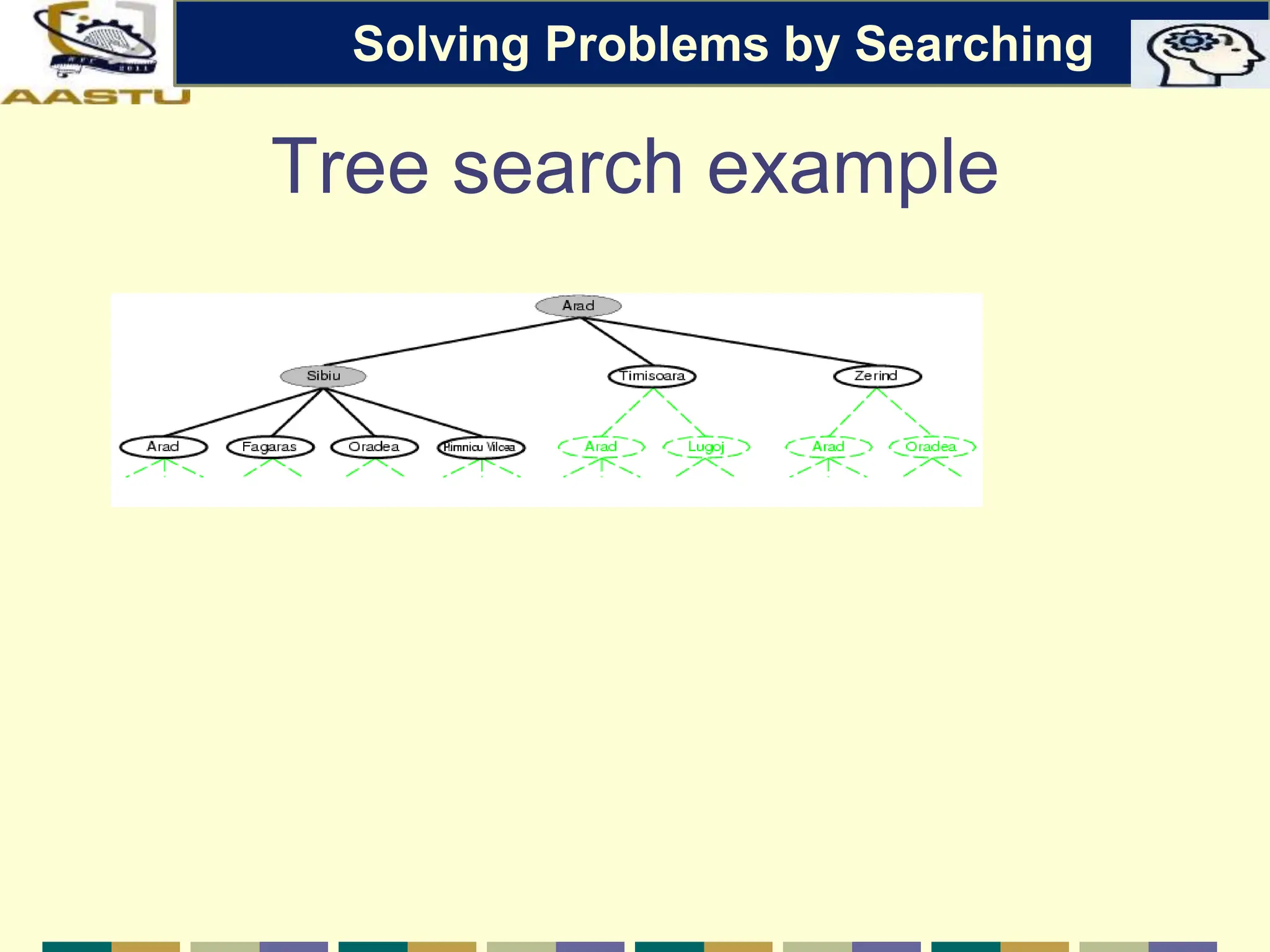
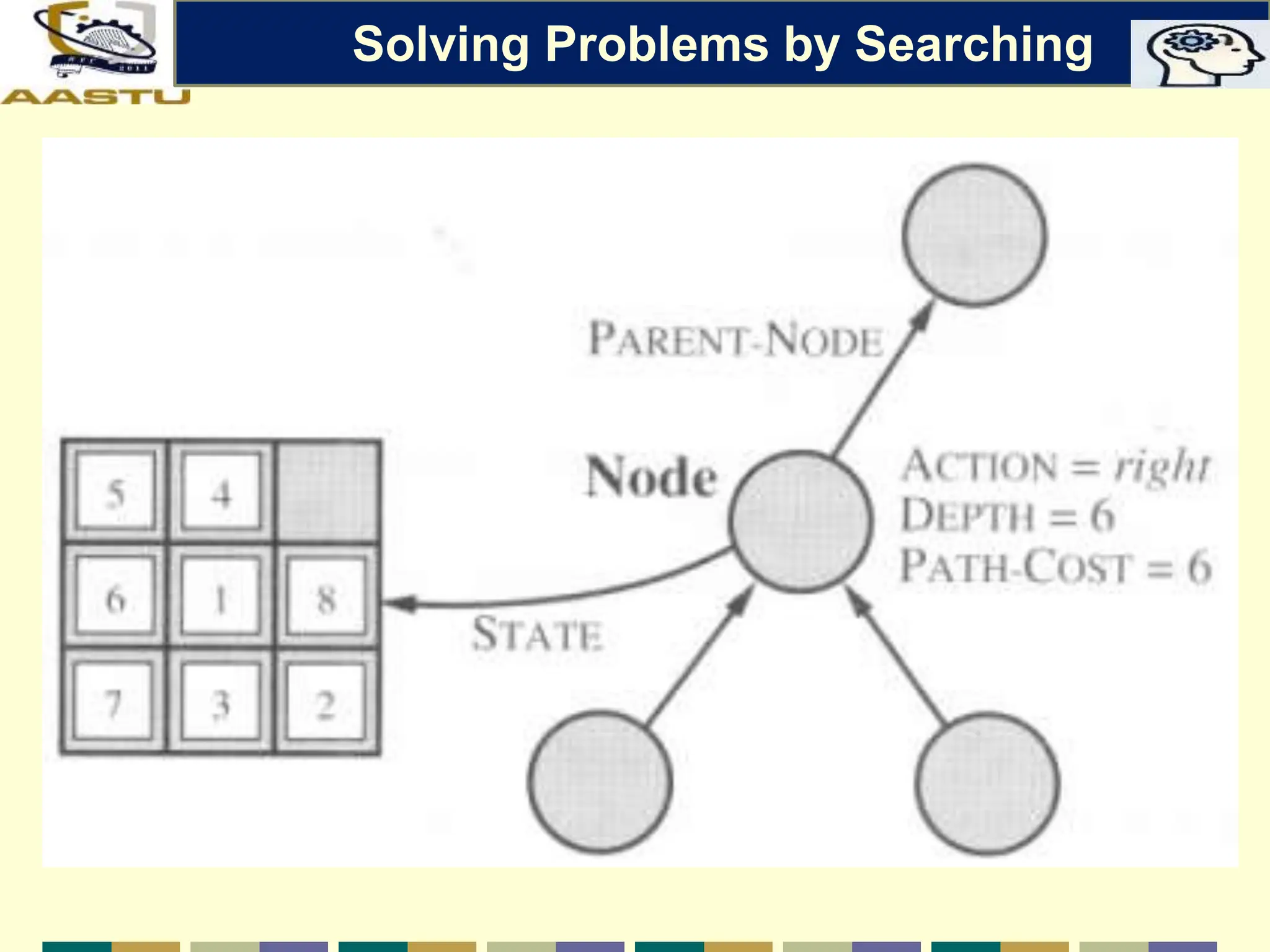
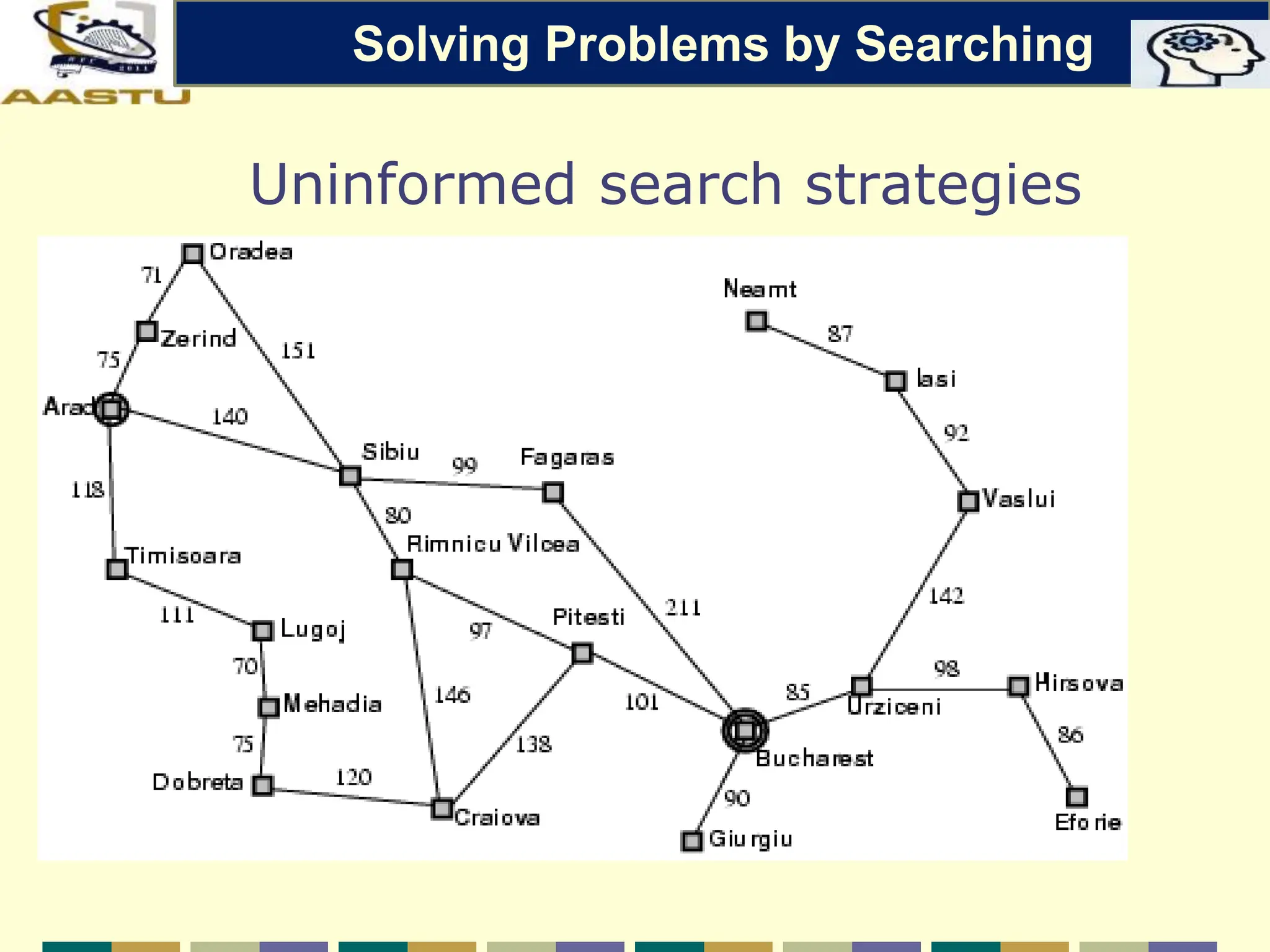
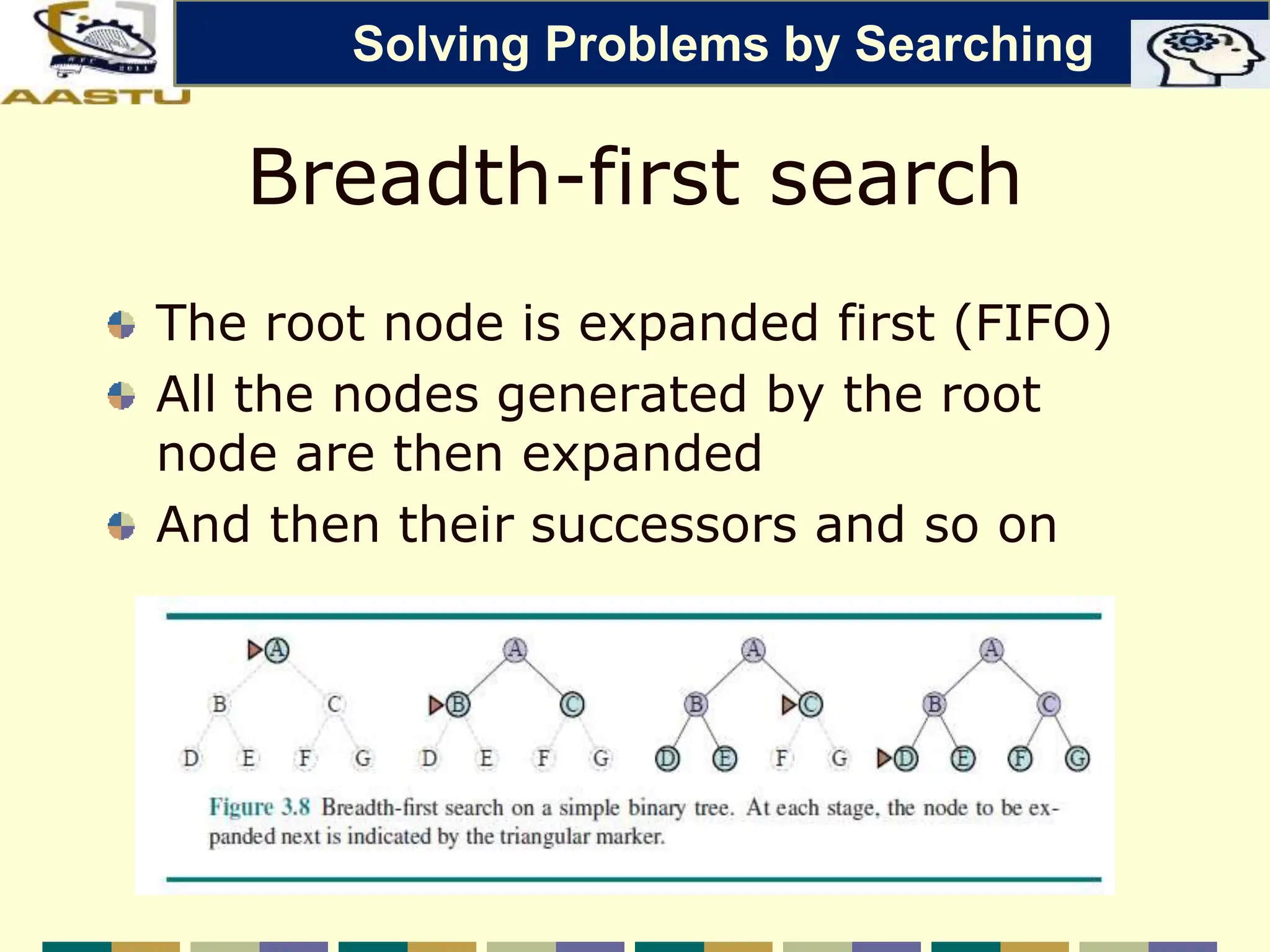
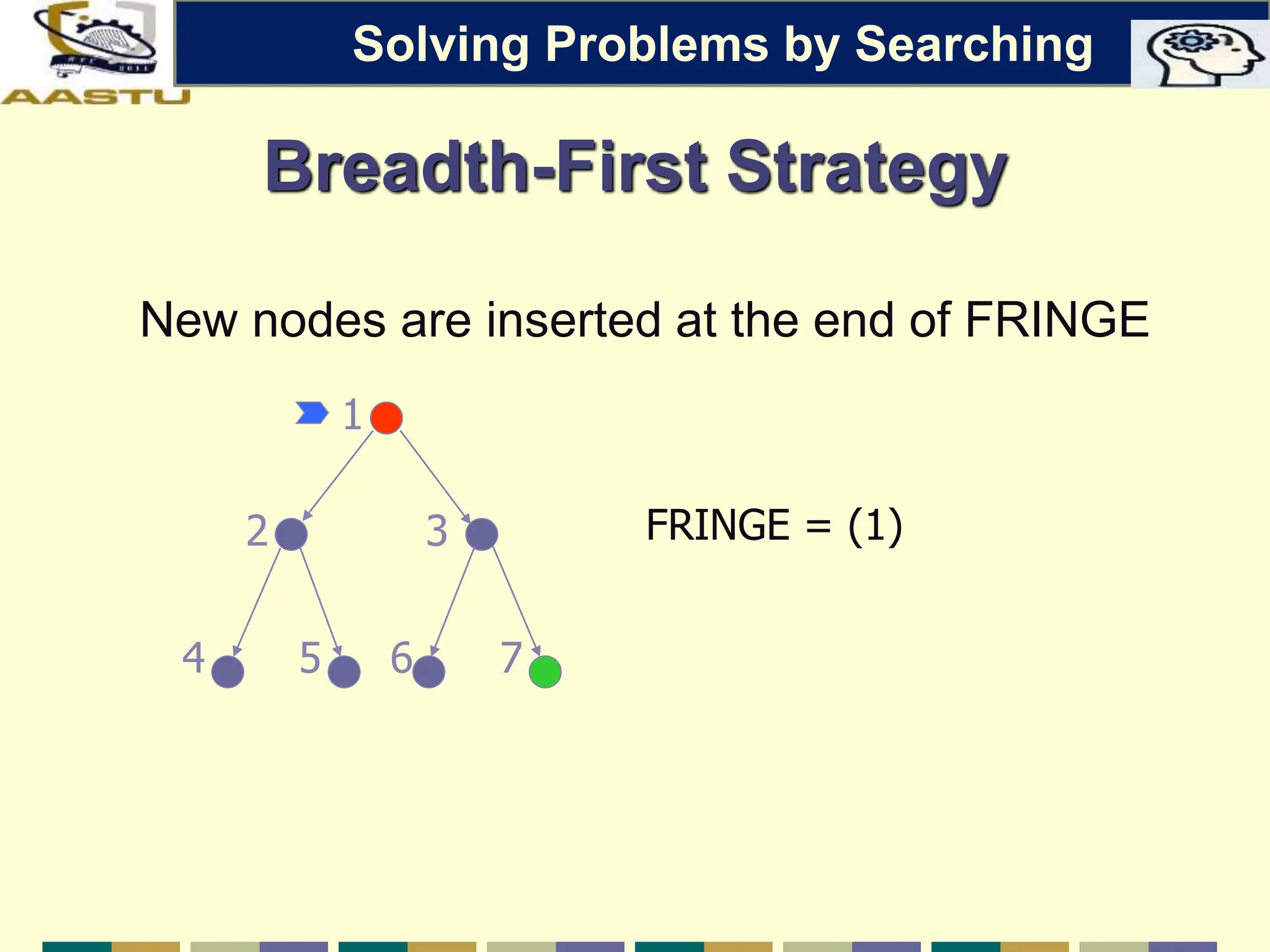
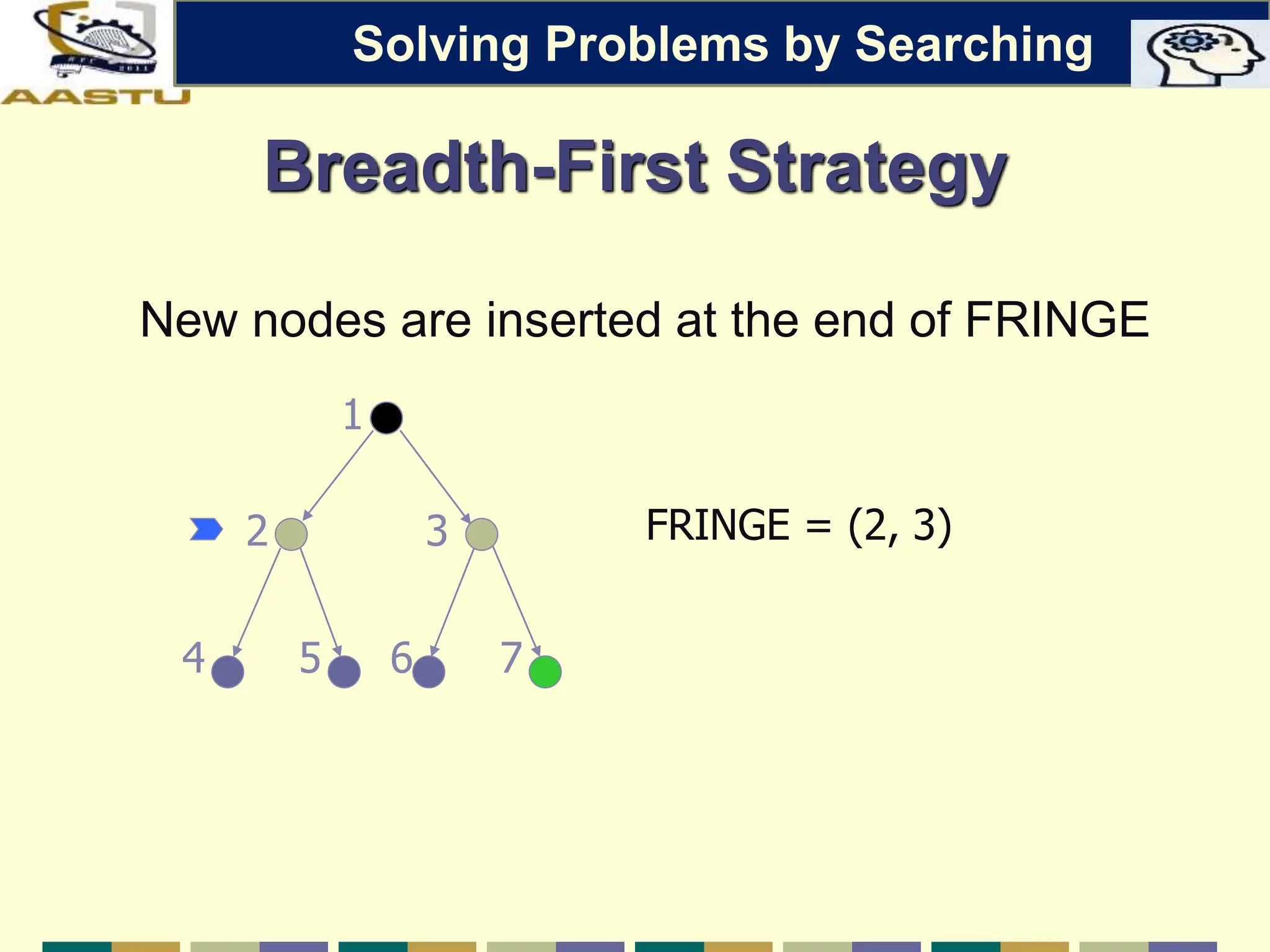
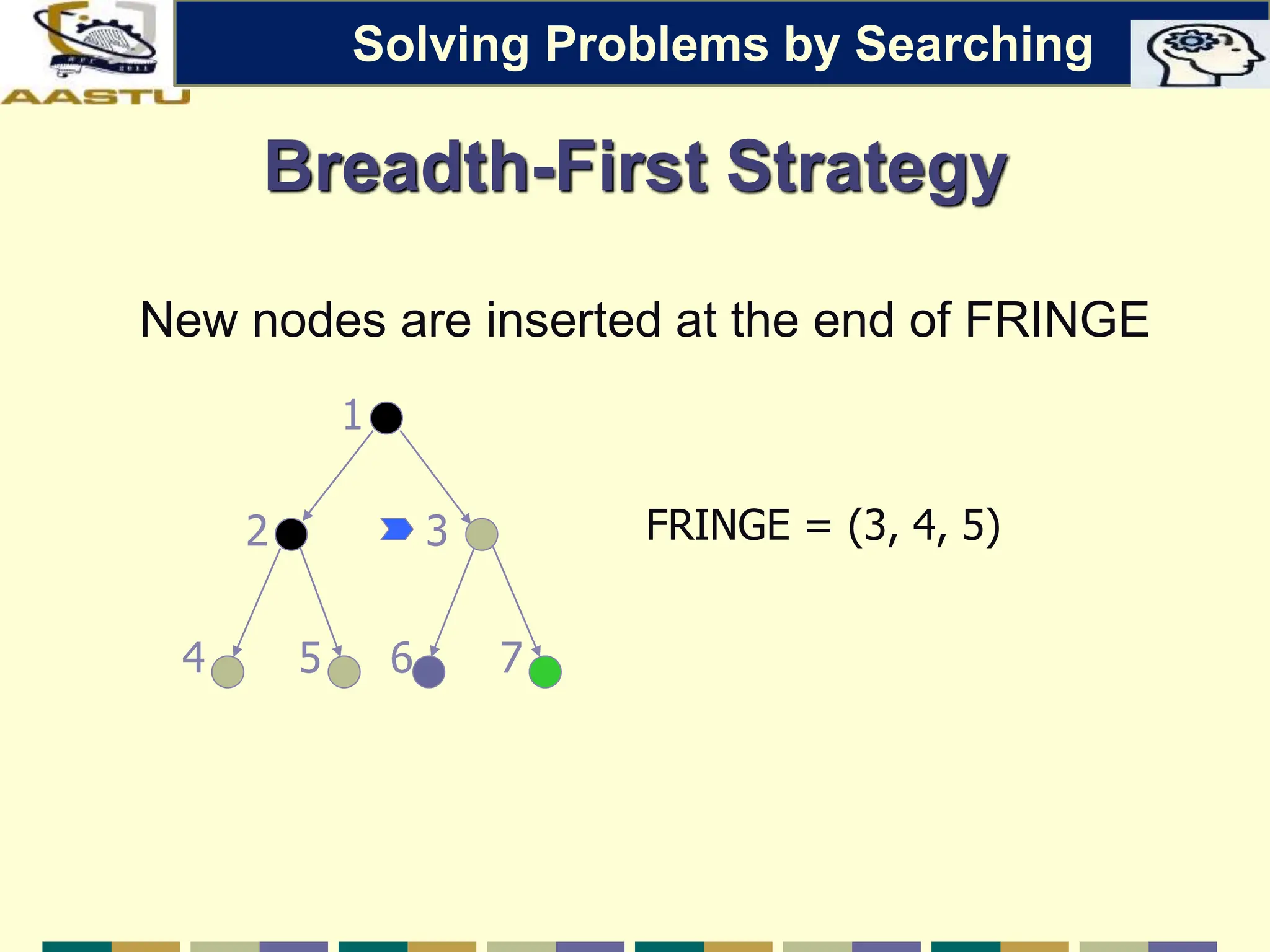
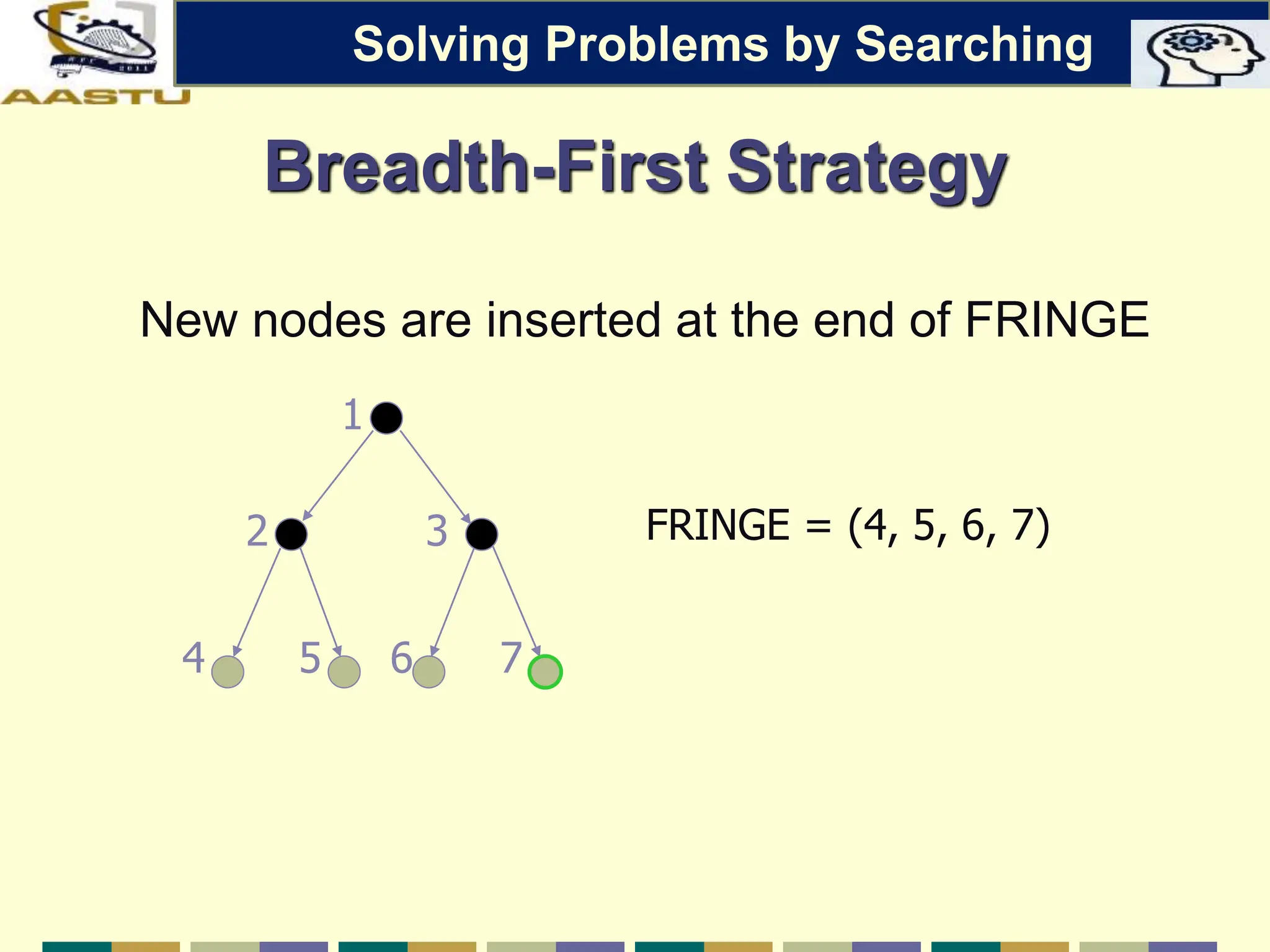
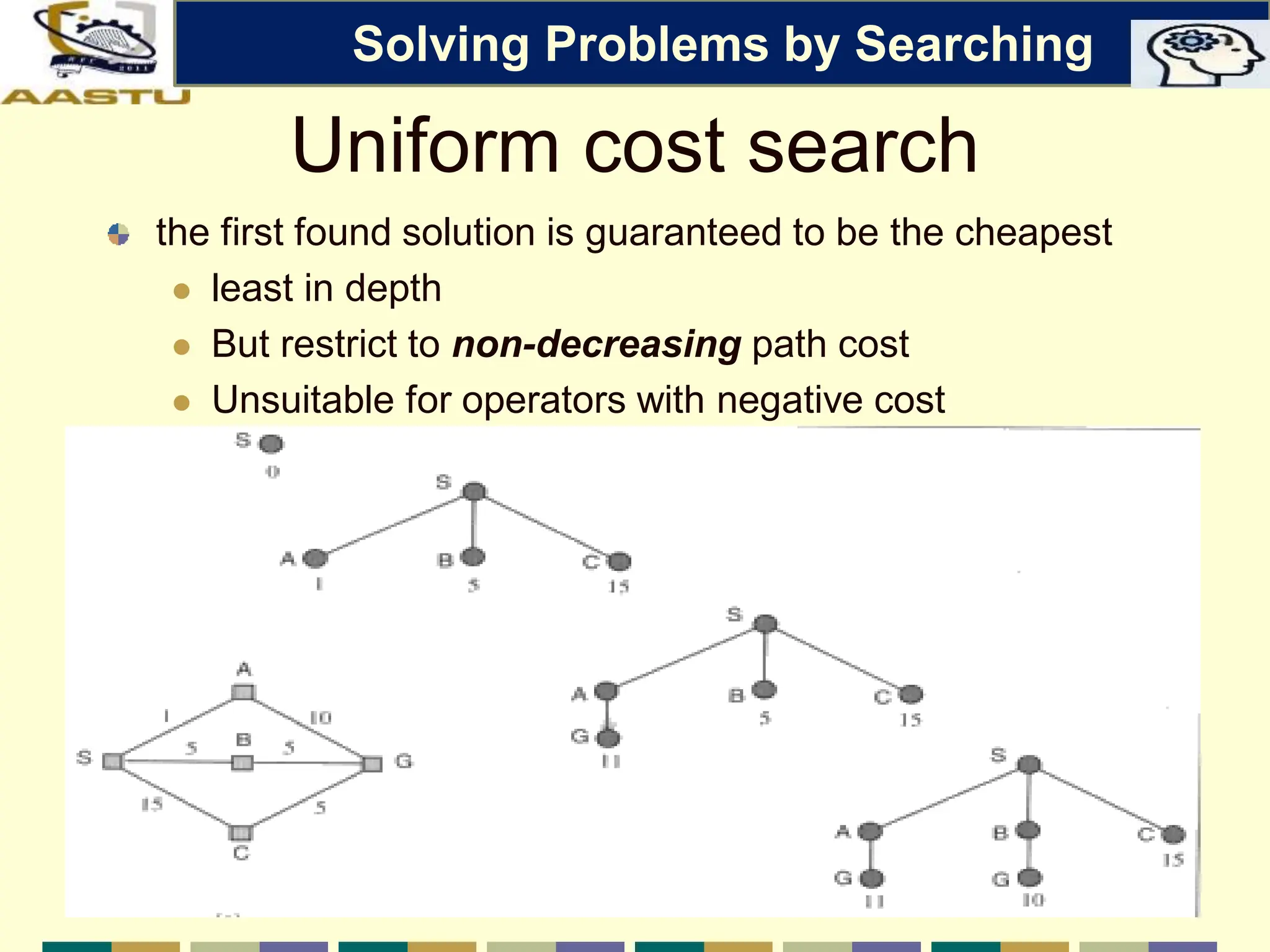
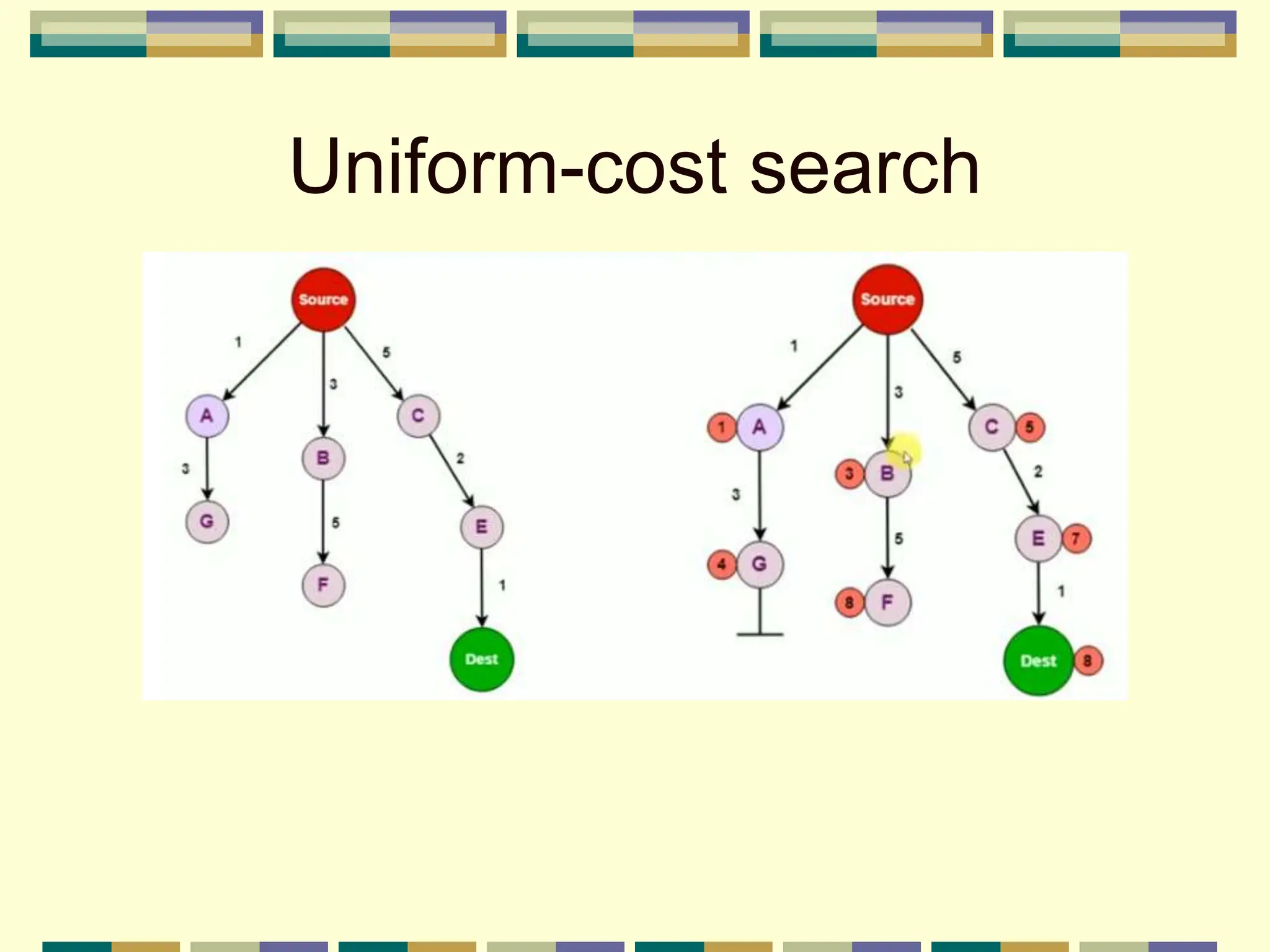
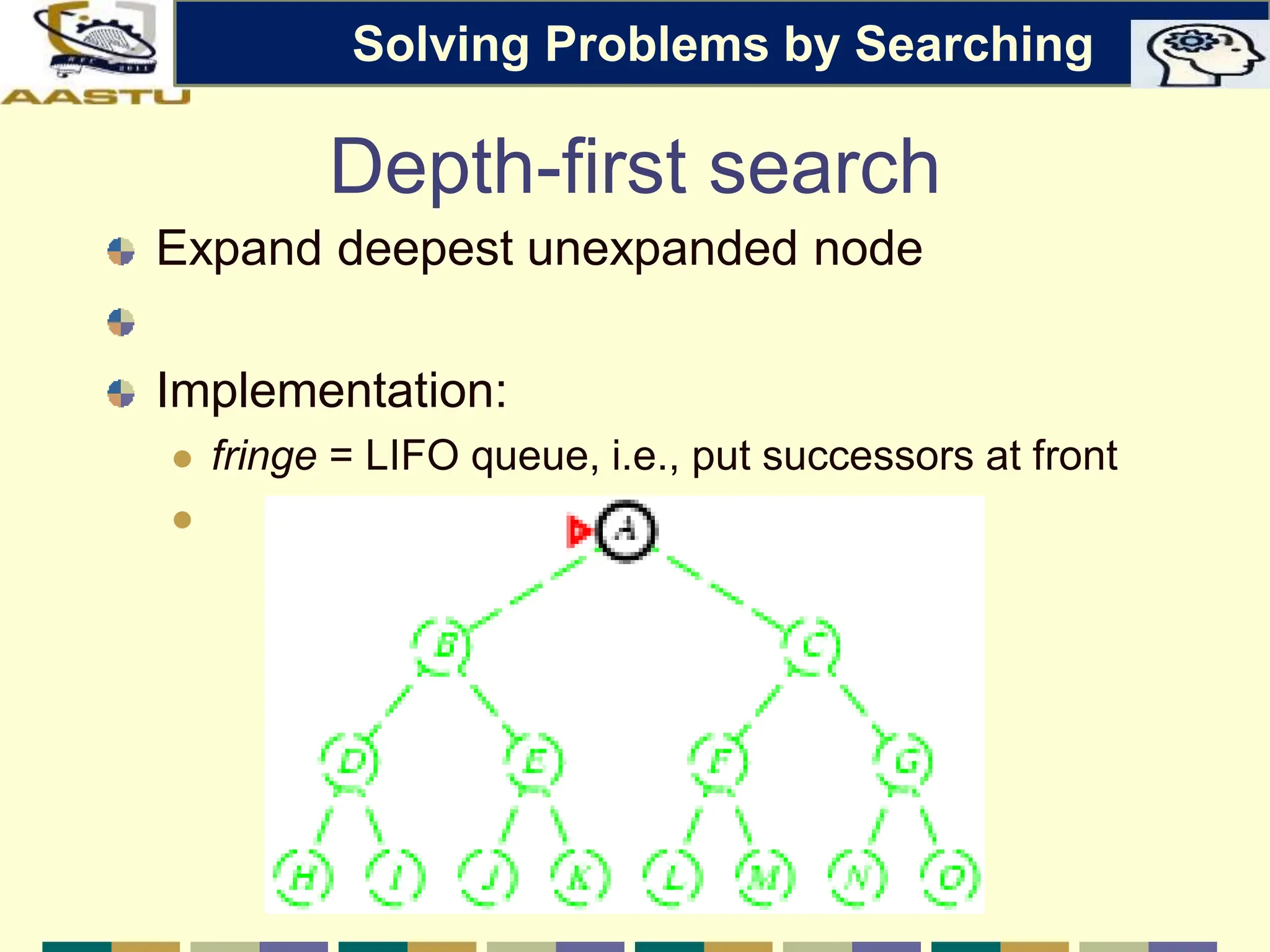
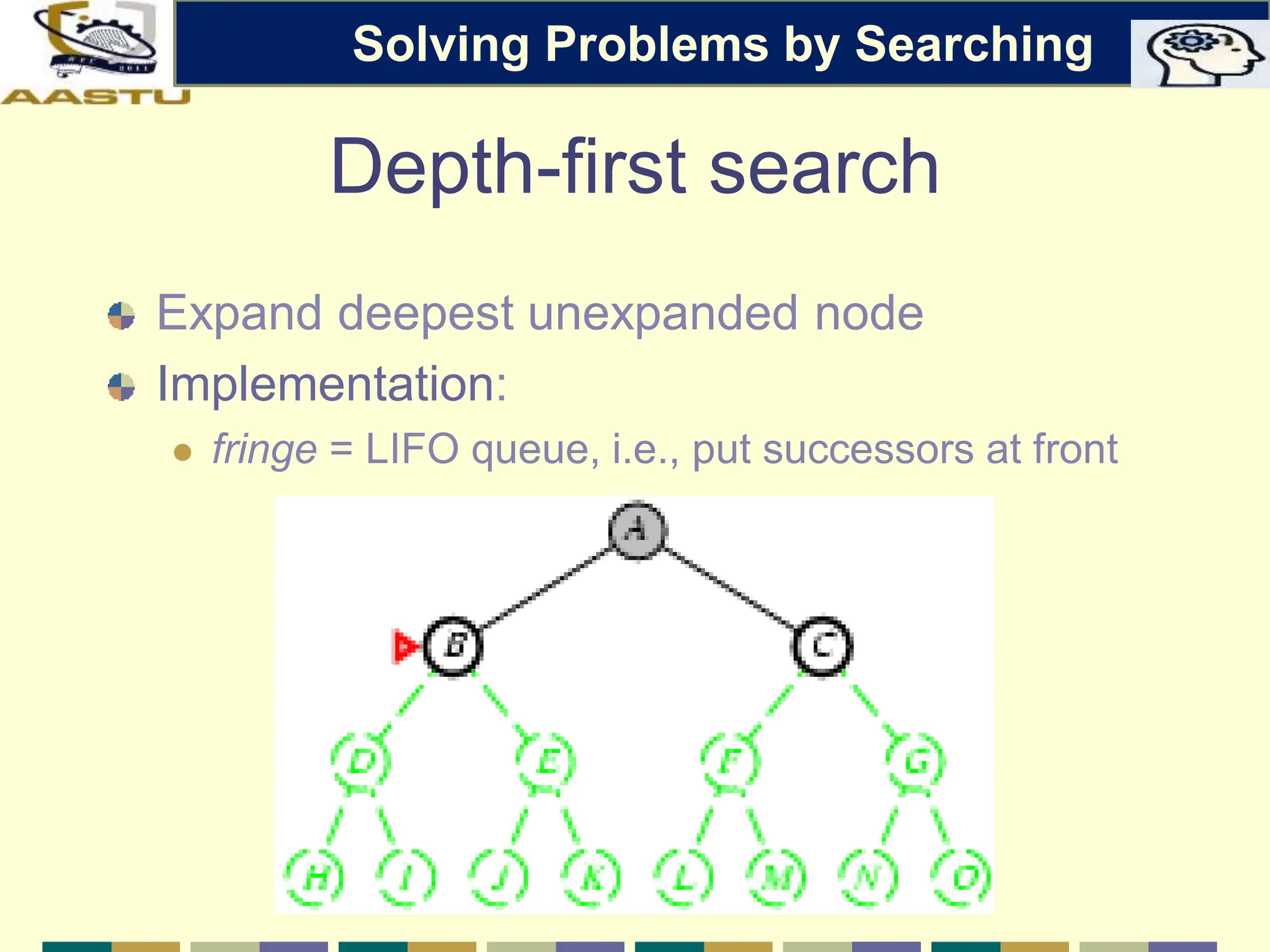
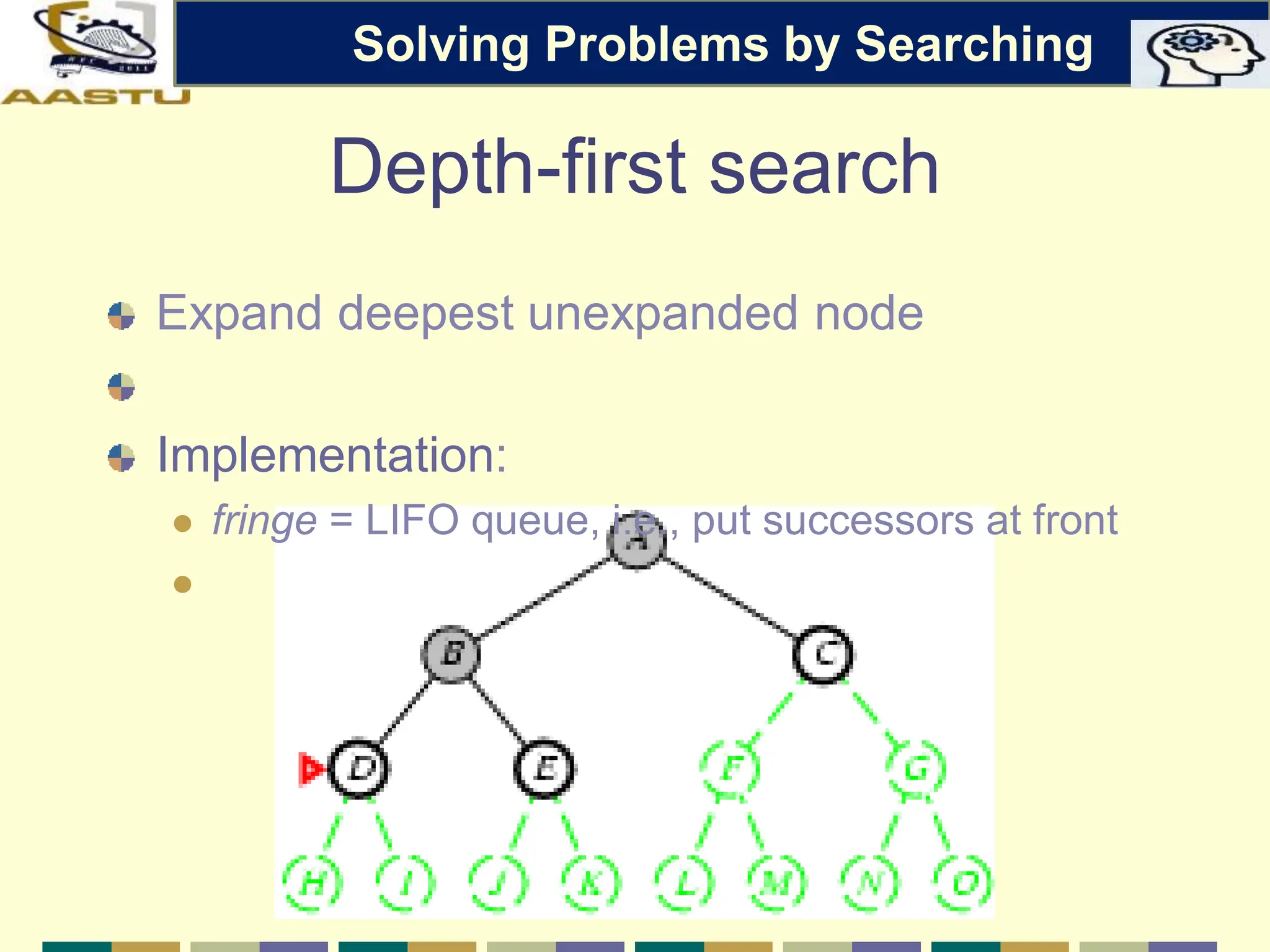
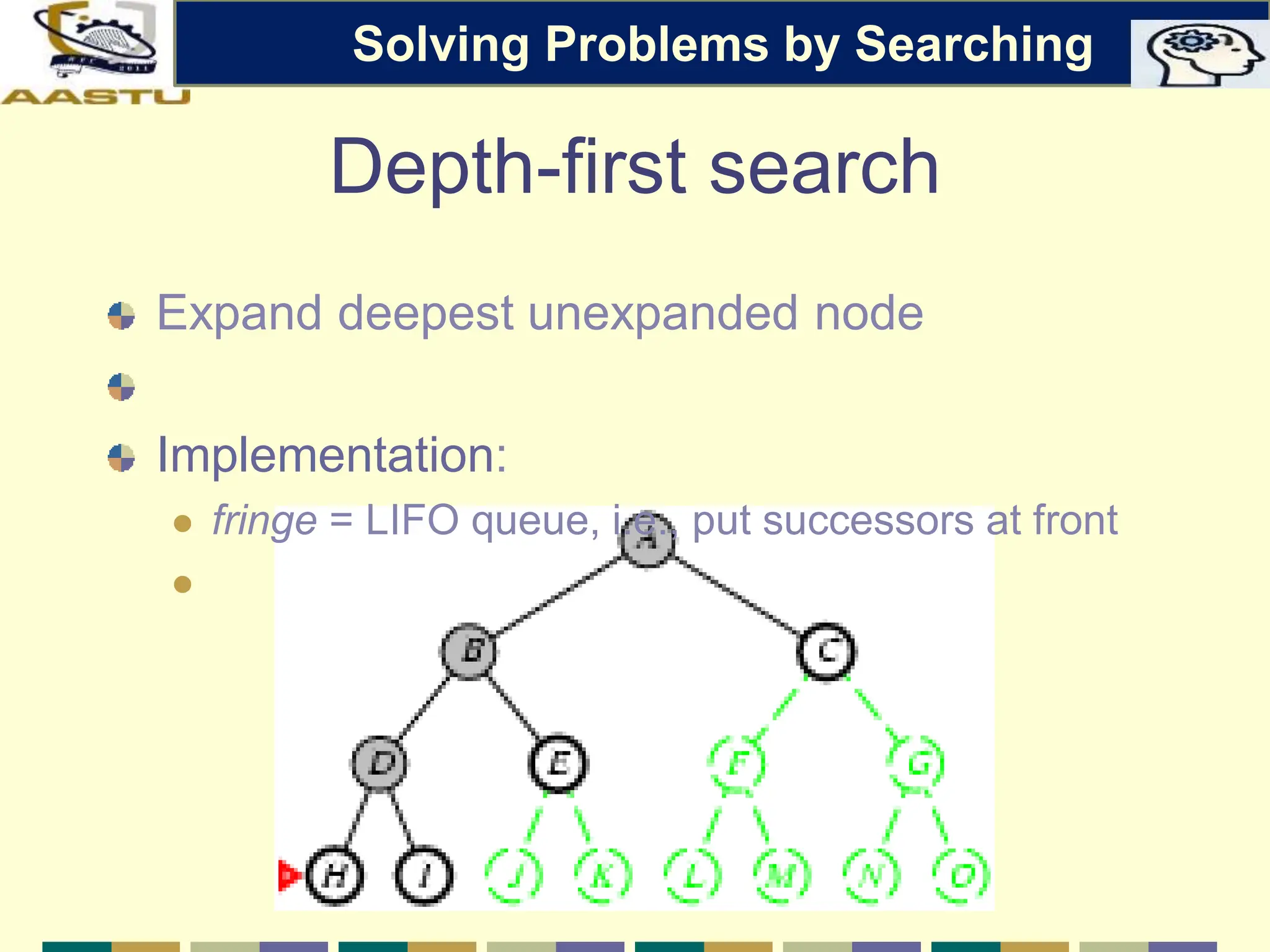
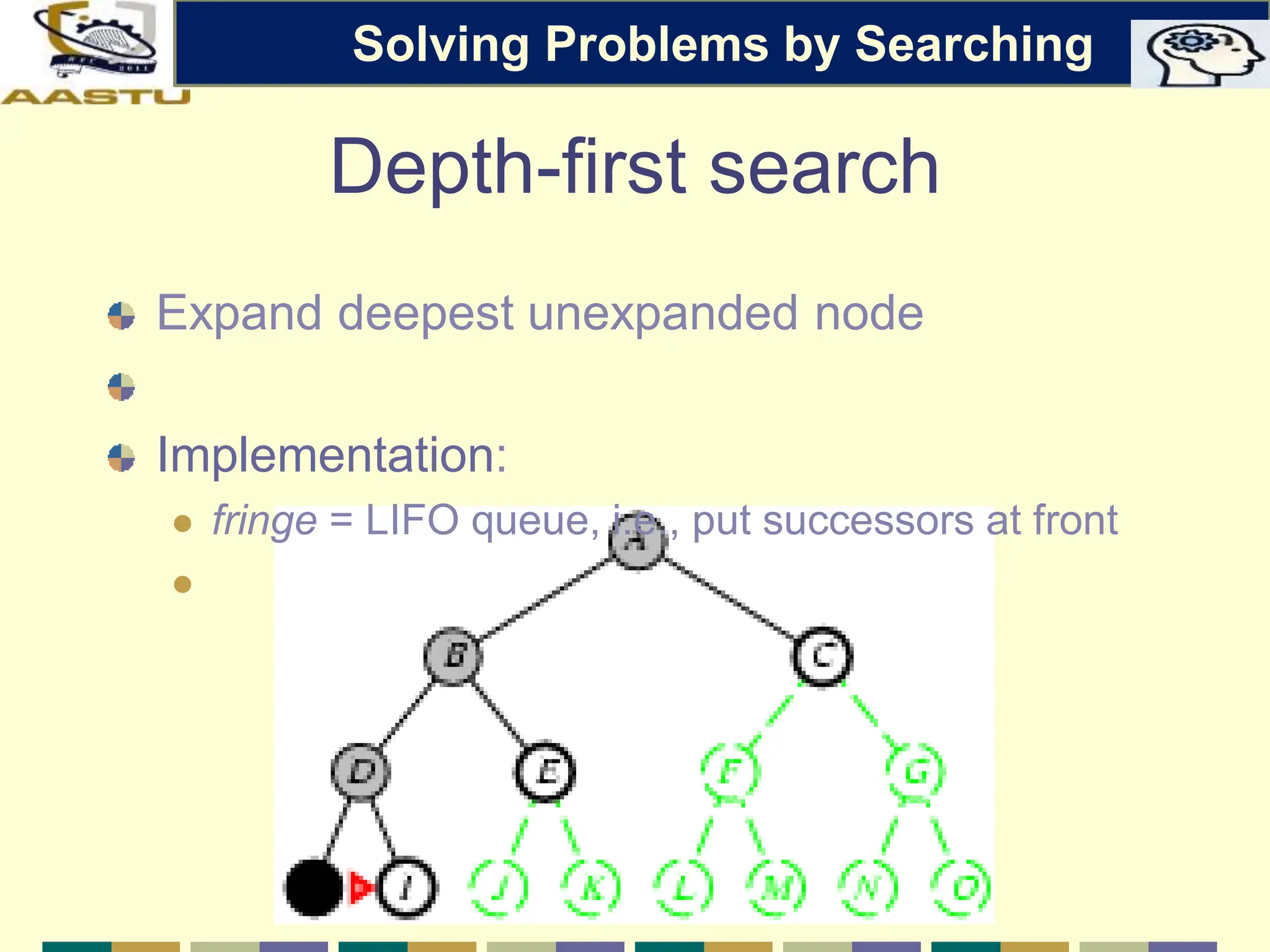
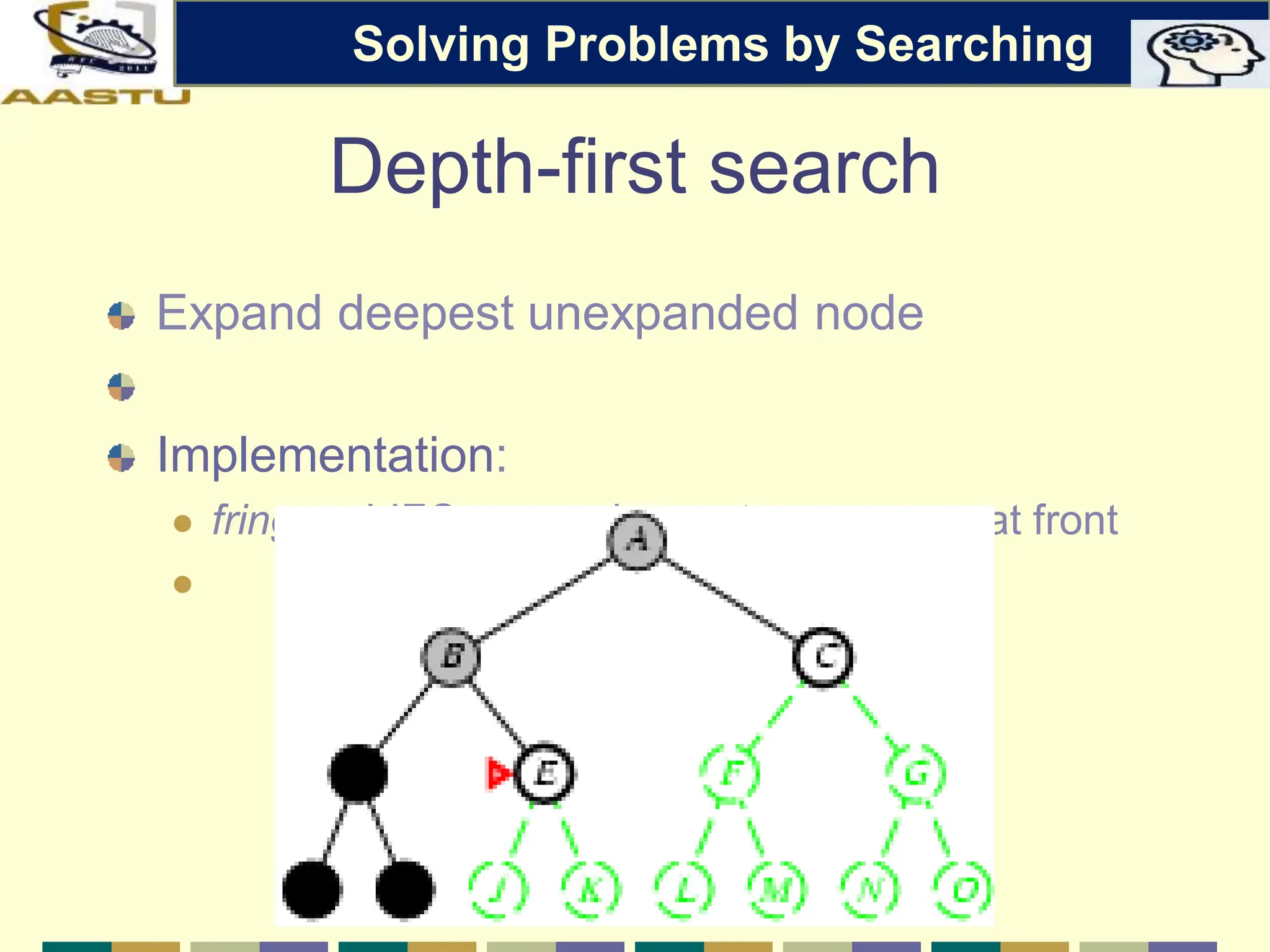
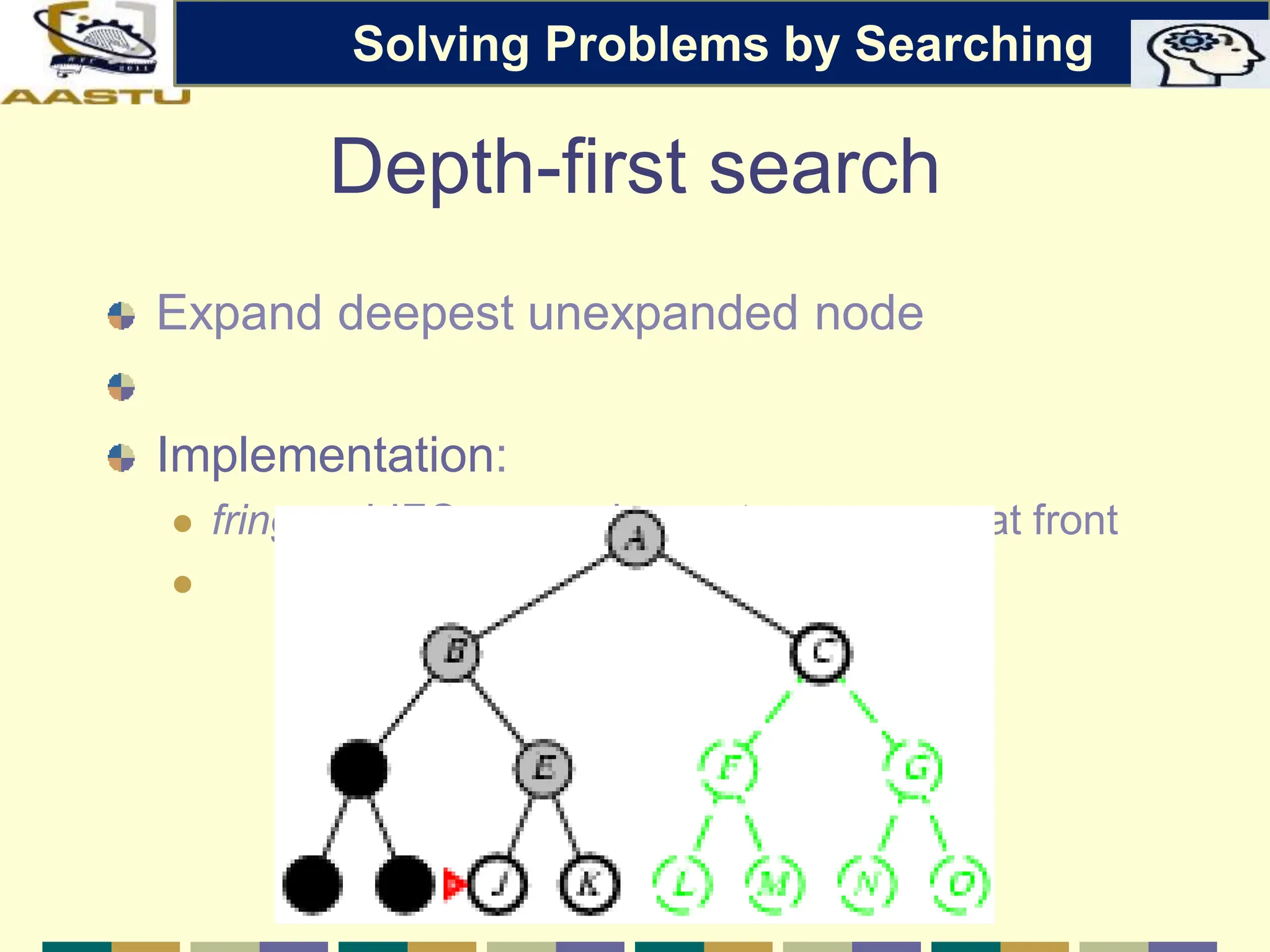
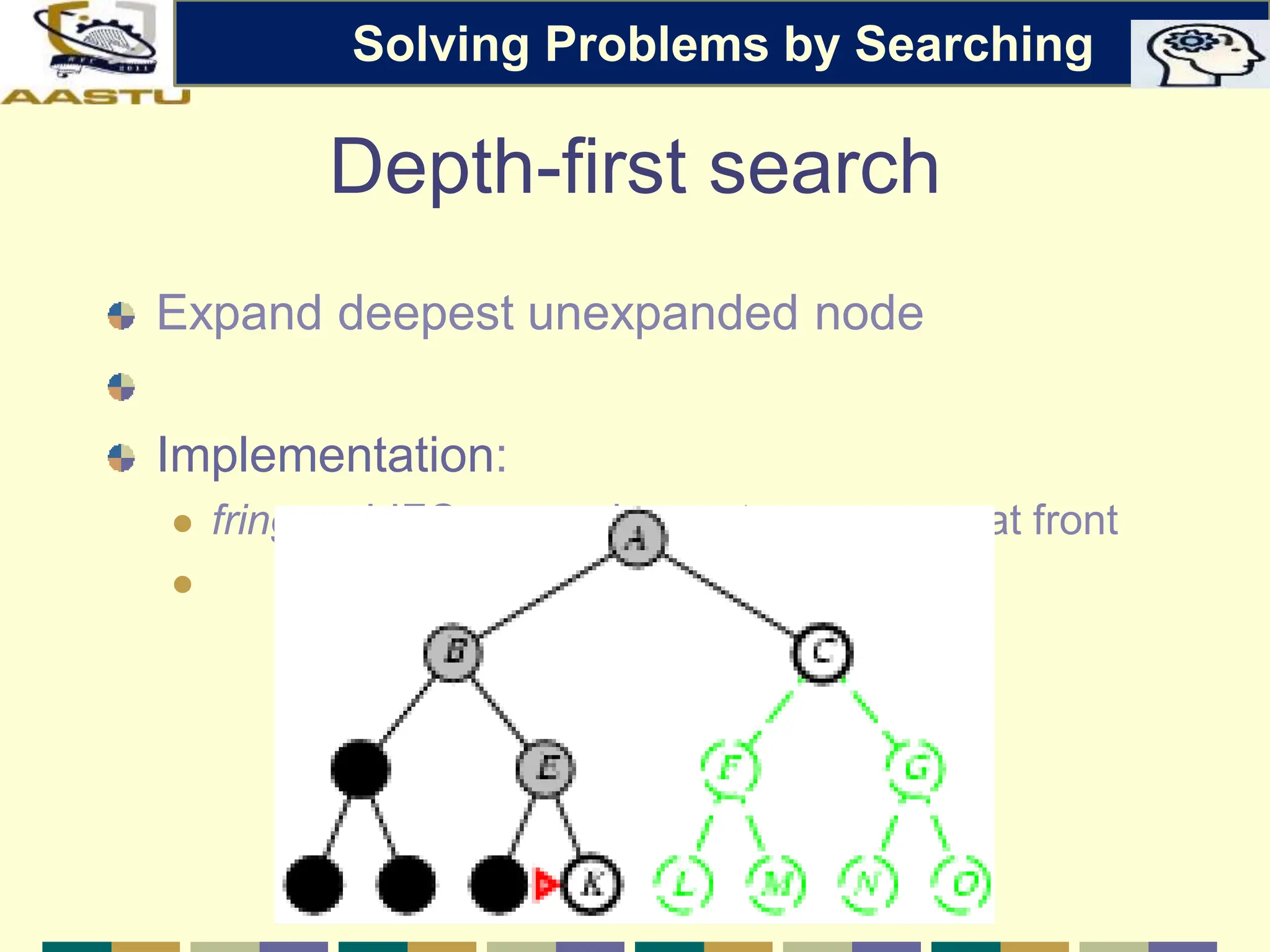
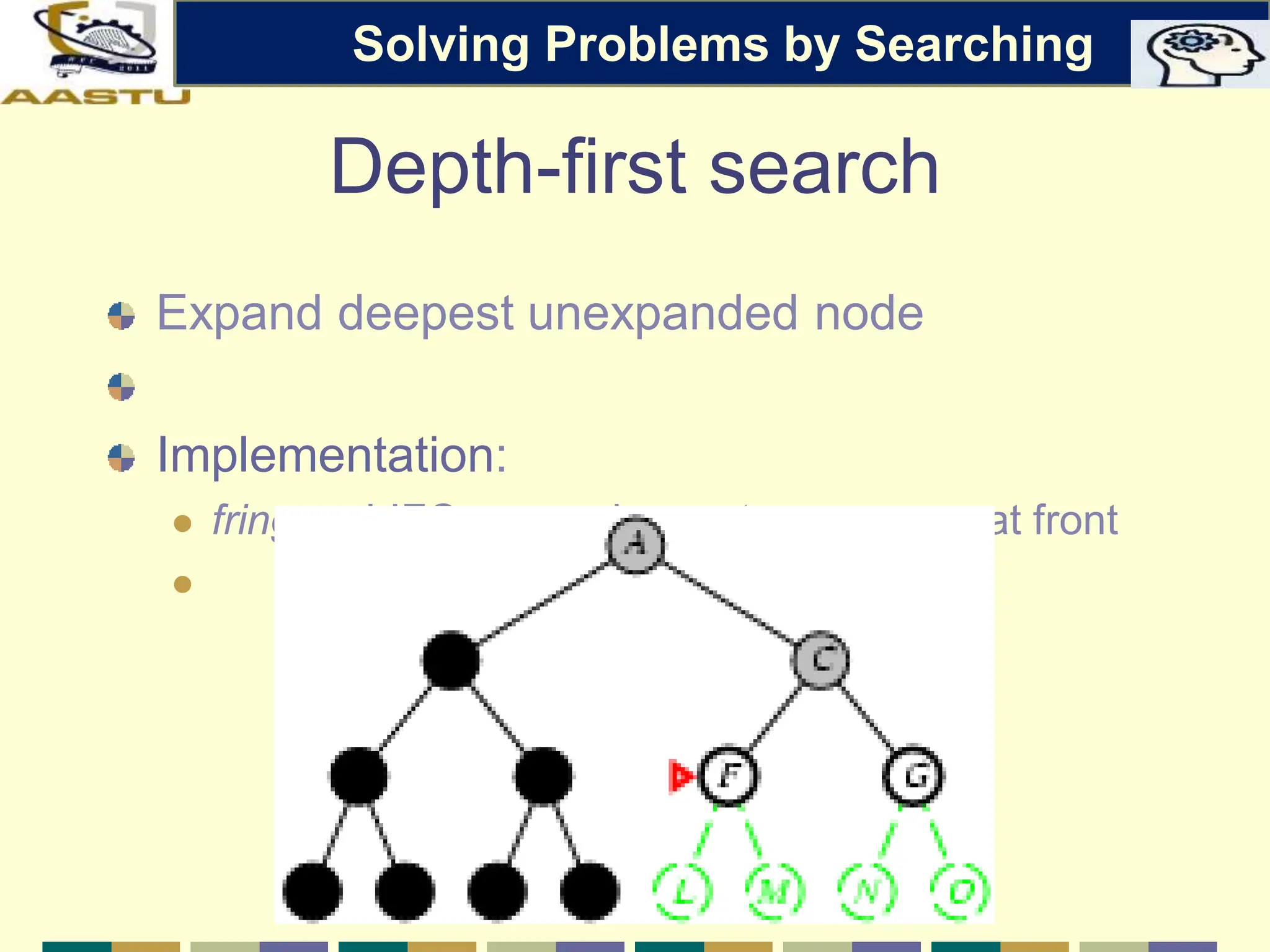
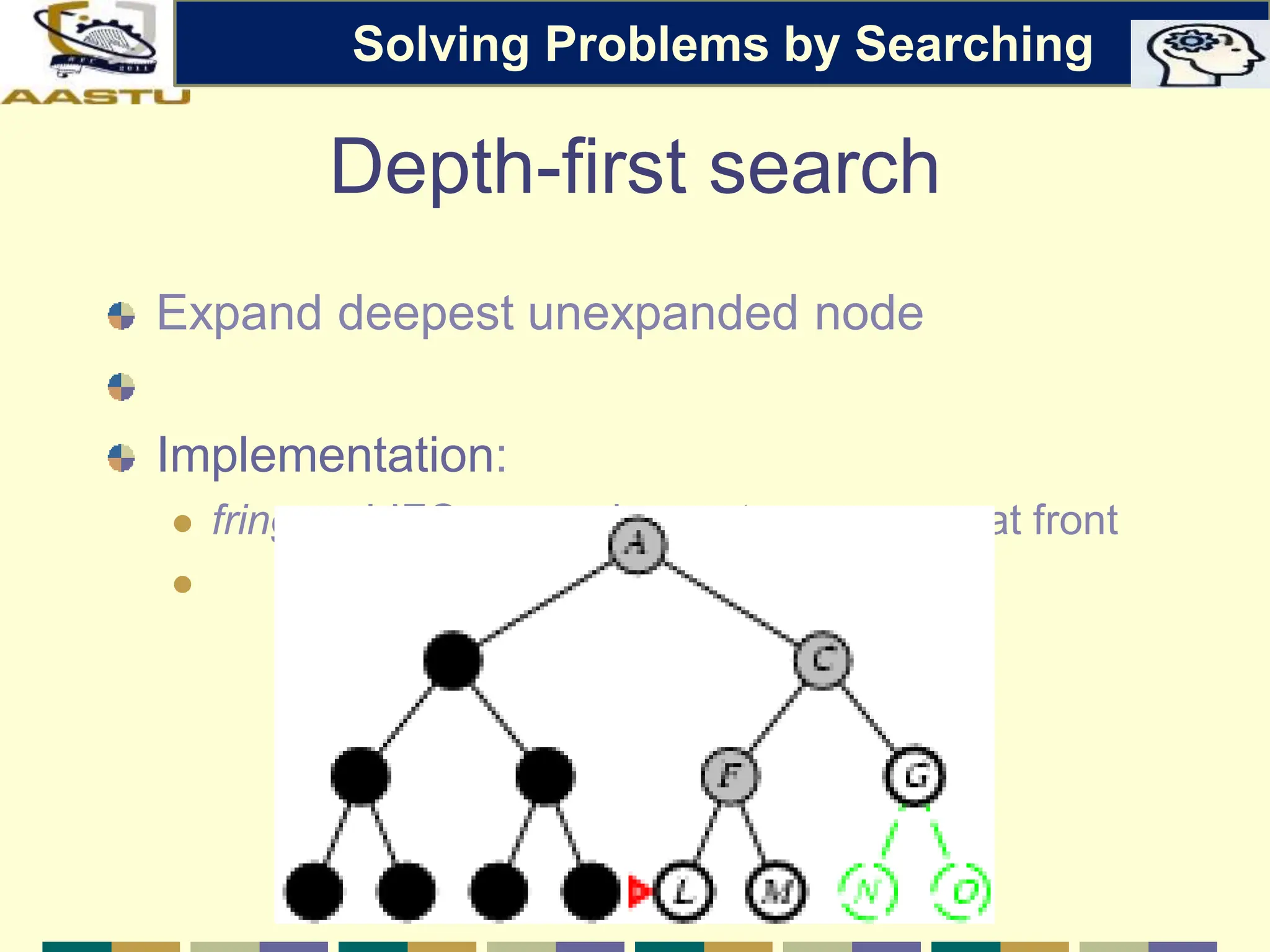
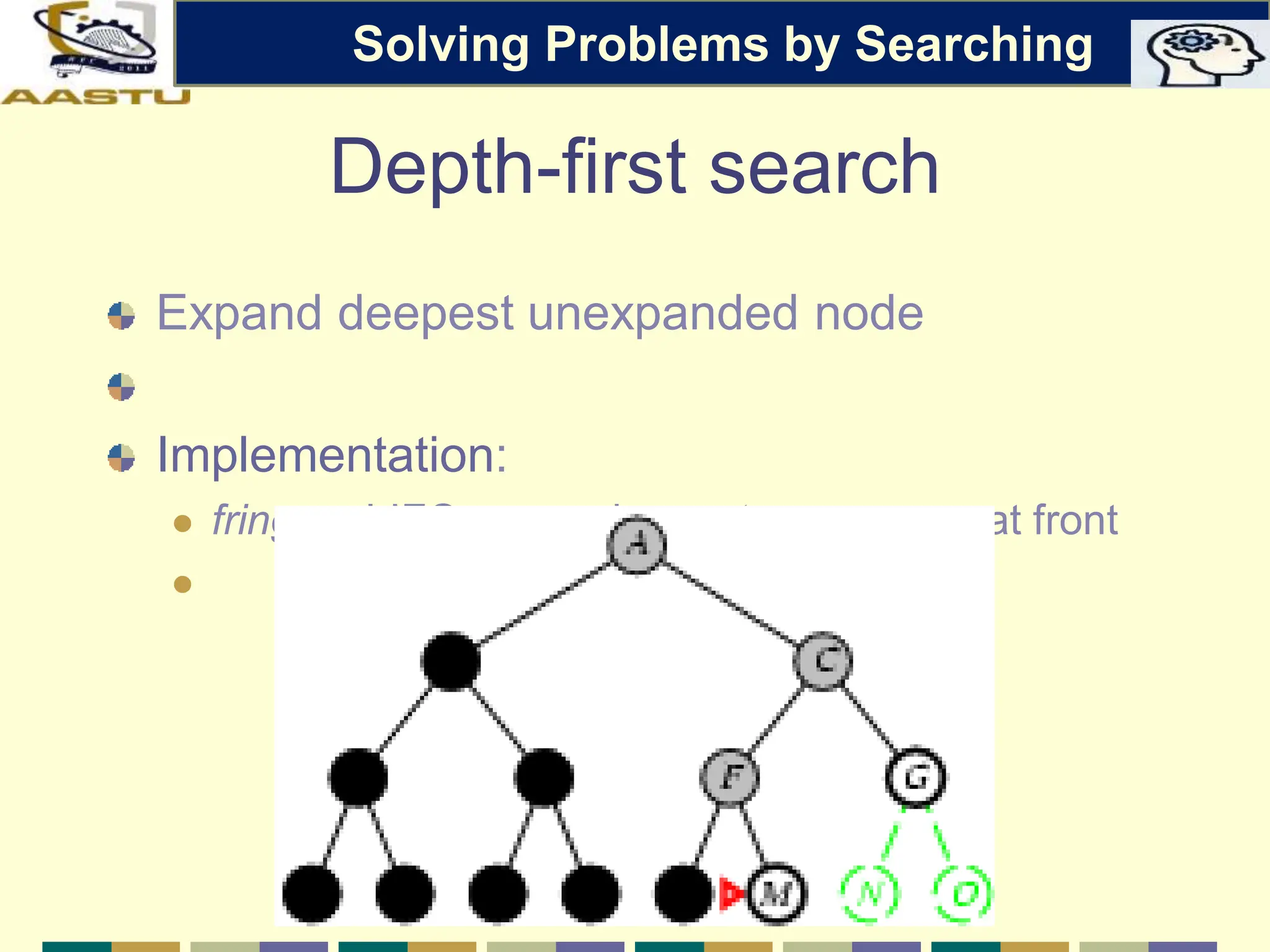
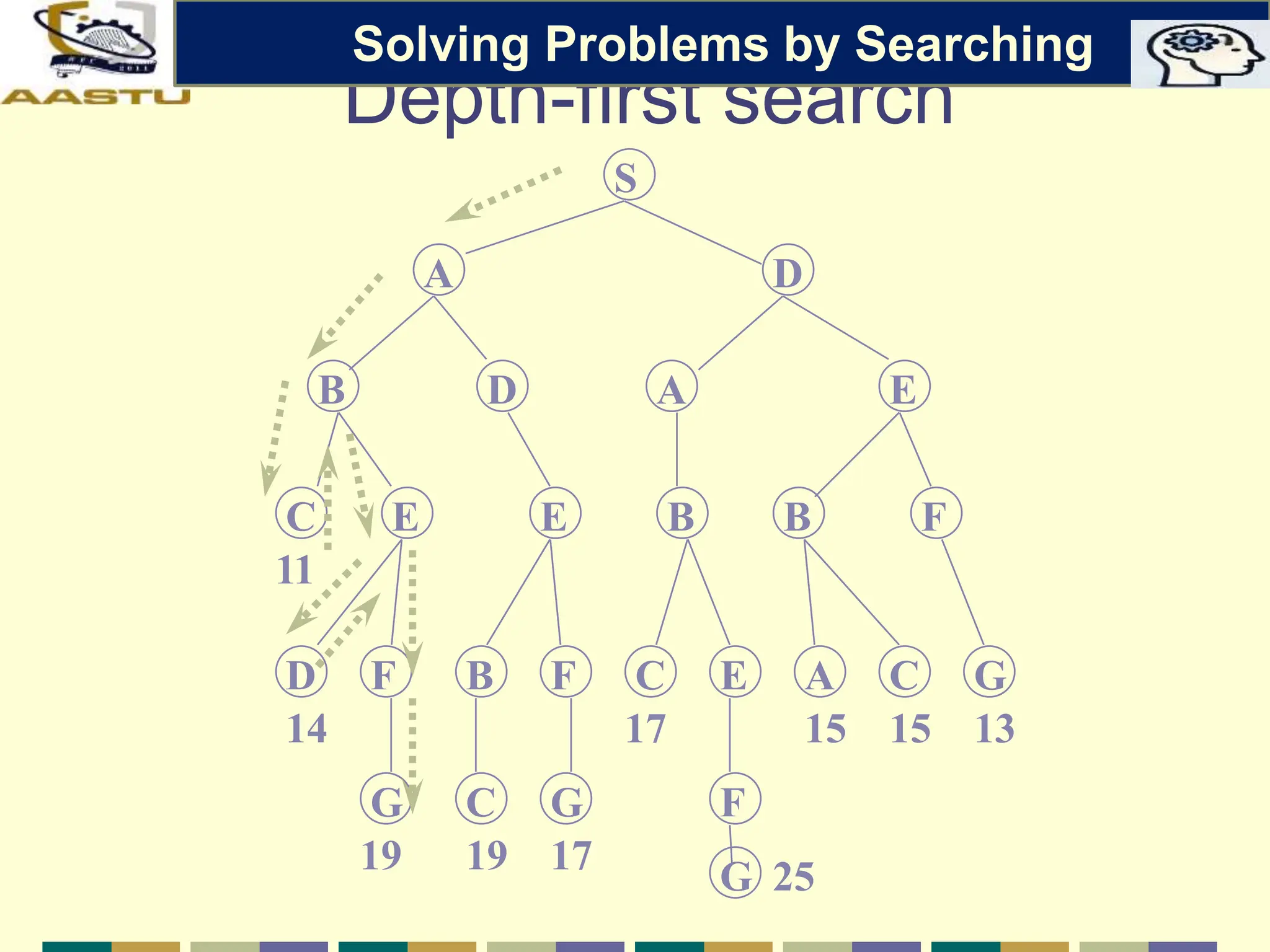
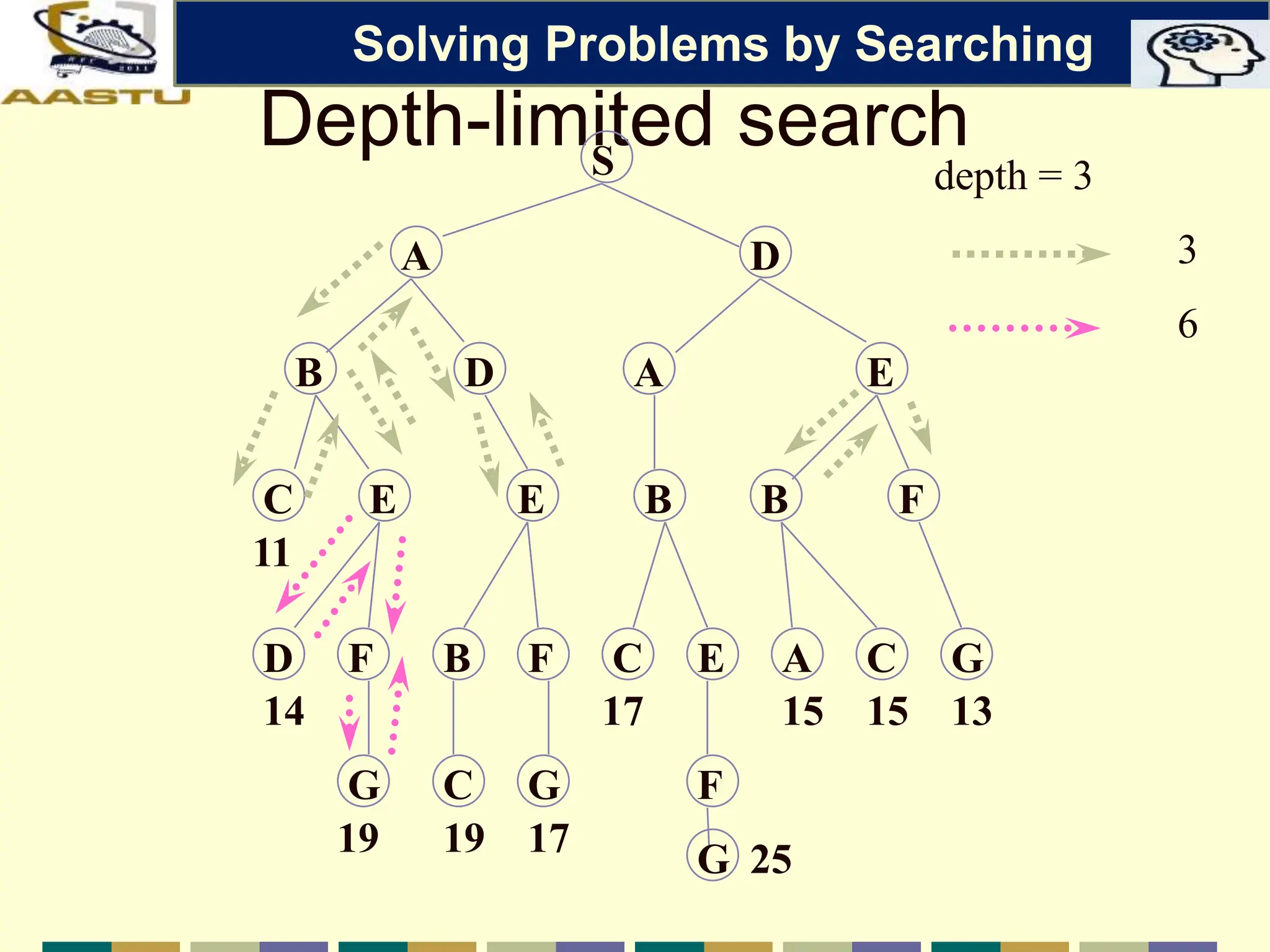
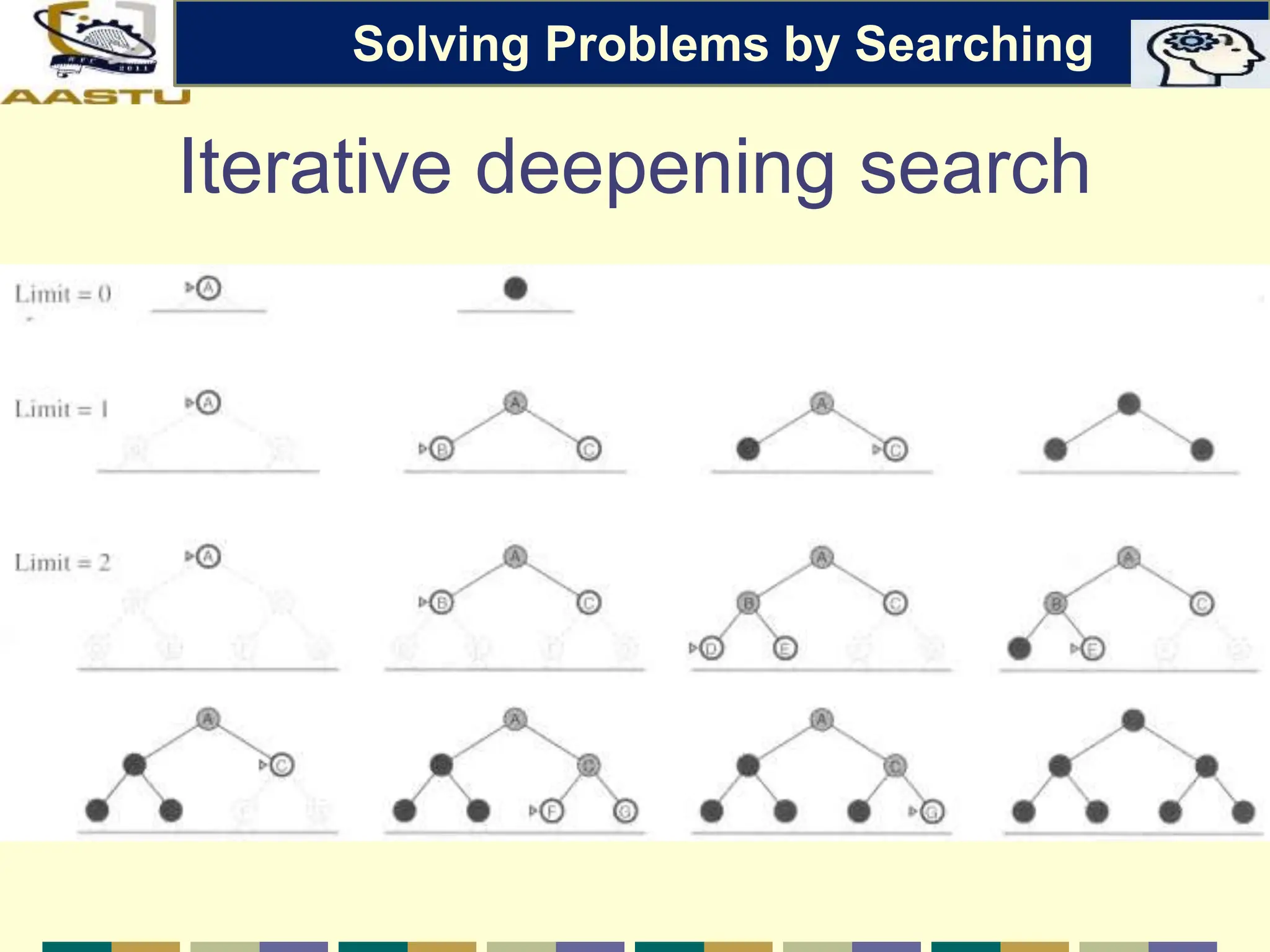
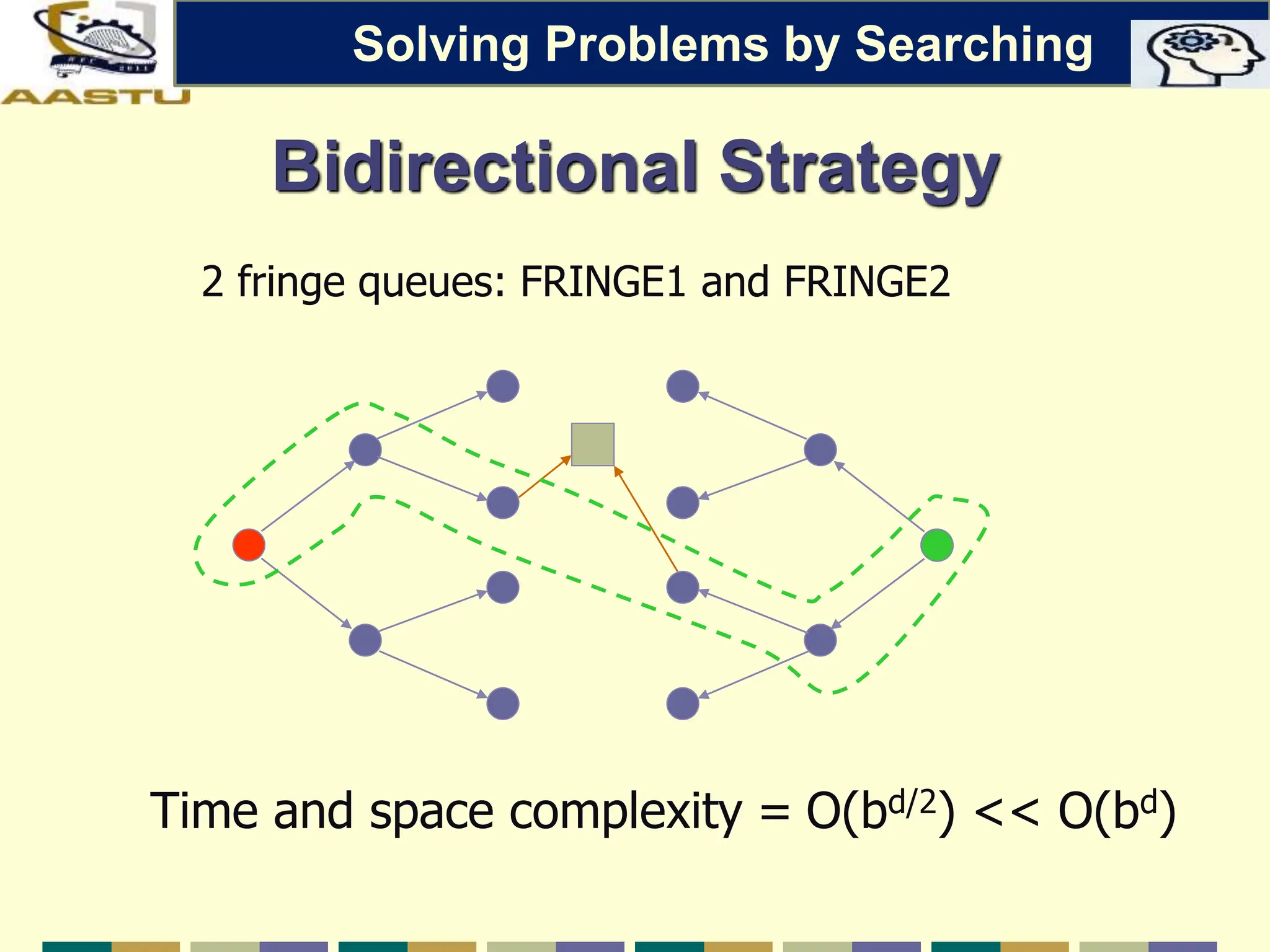
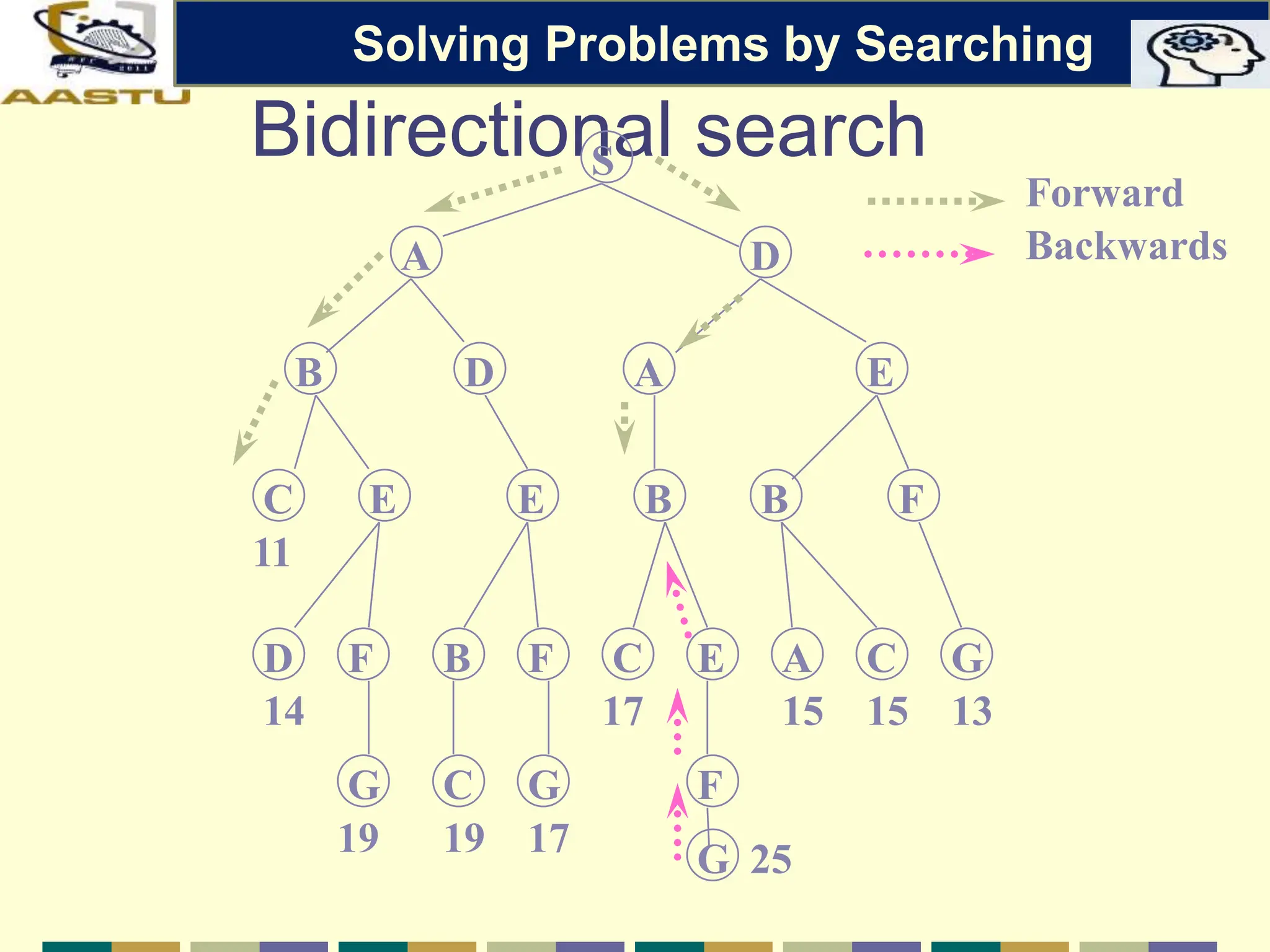
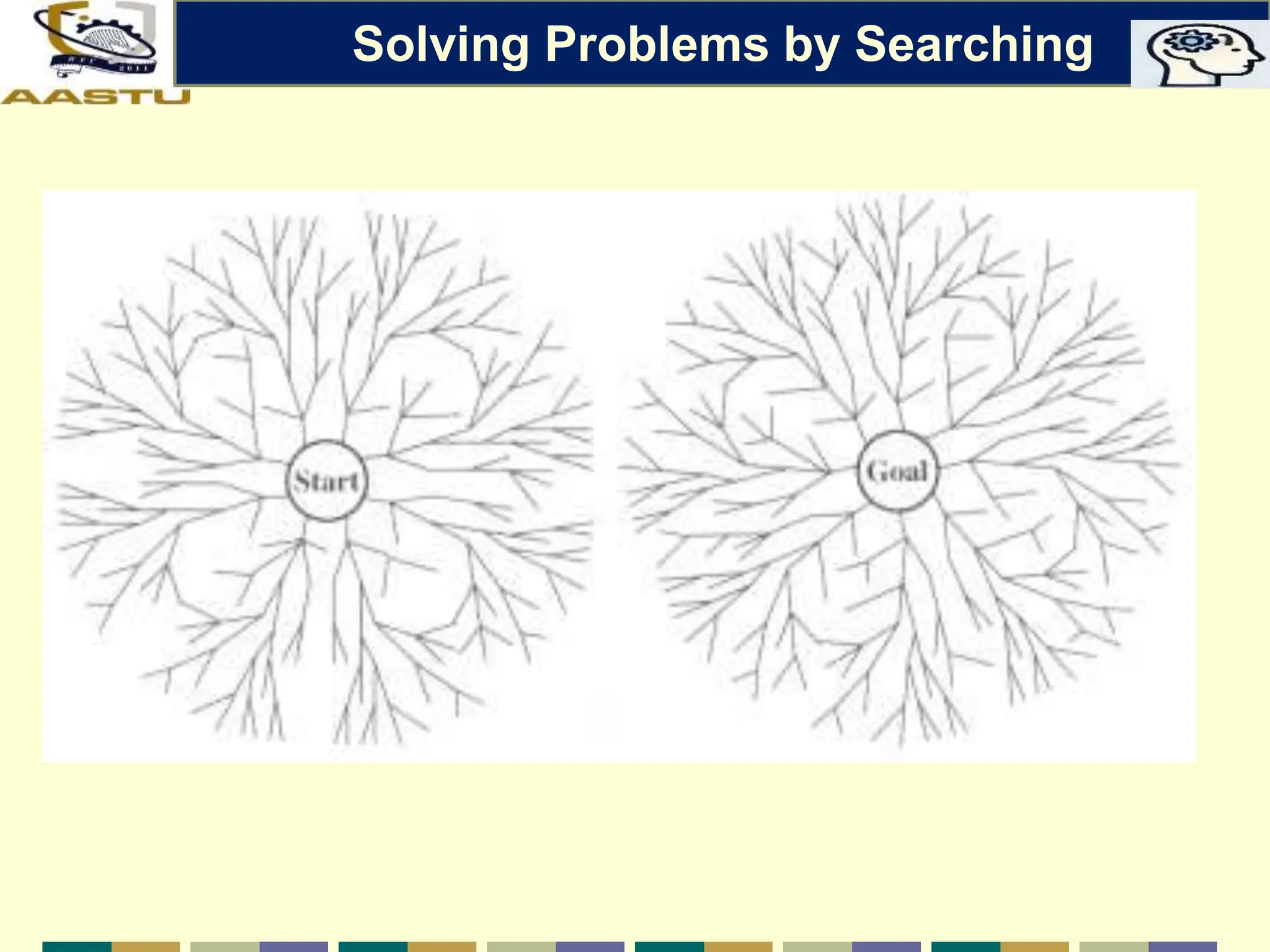
The document discusses problem-solving agents in AI, describing their function of formulating goals, defining problems, and employing search algorithms to find solutions. Key concepts include the structure of agents, various types of search strategies, and the formulation of problems using a set of components such as initial state and path cost. It also differentiates between uninformed and informed search strategies, highlighting their characteristics and challenges.