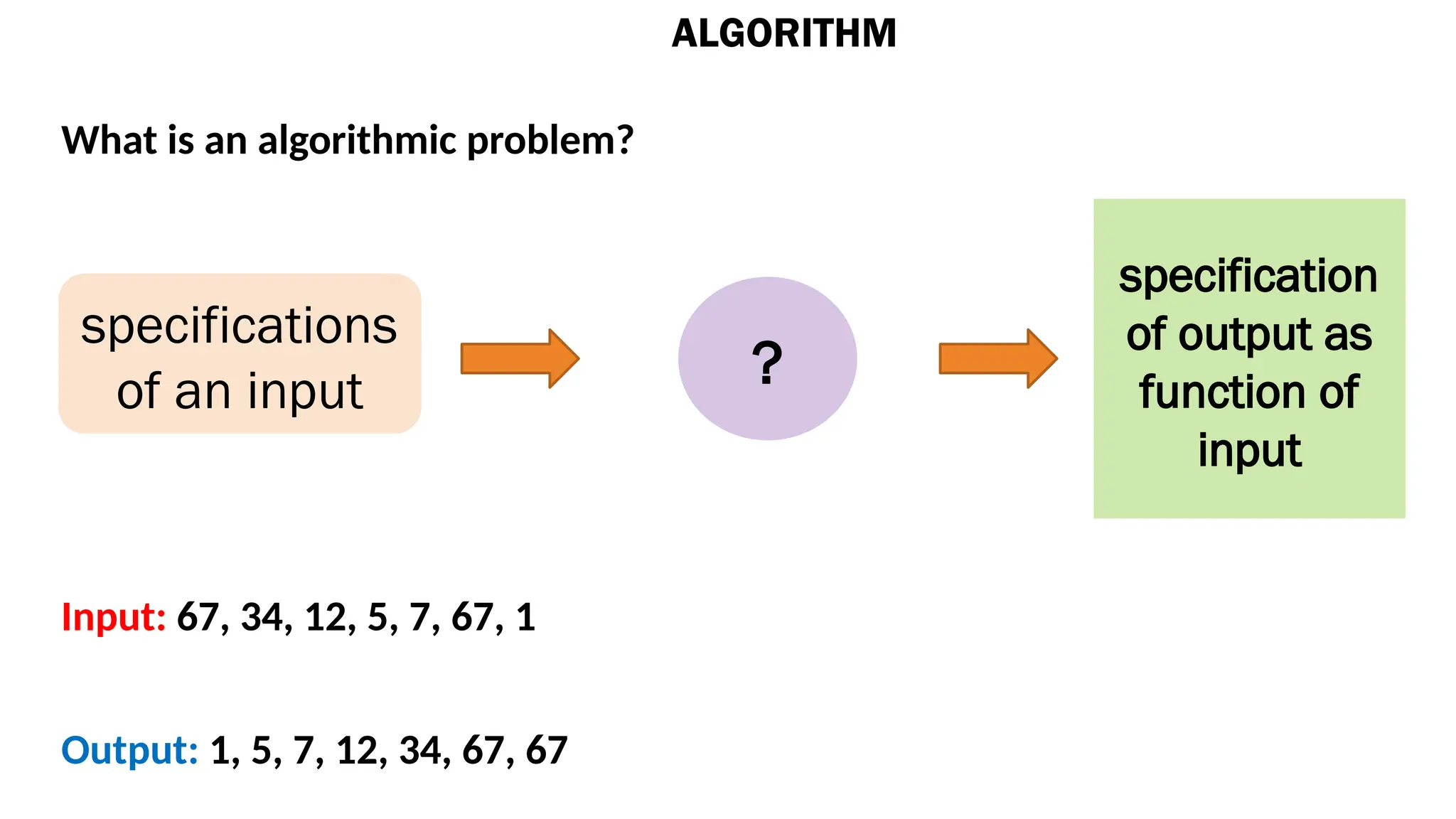
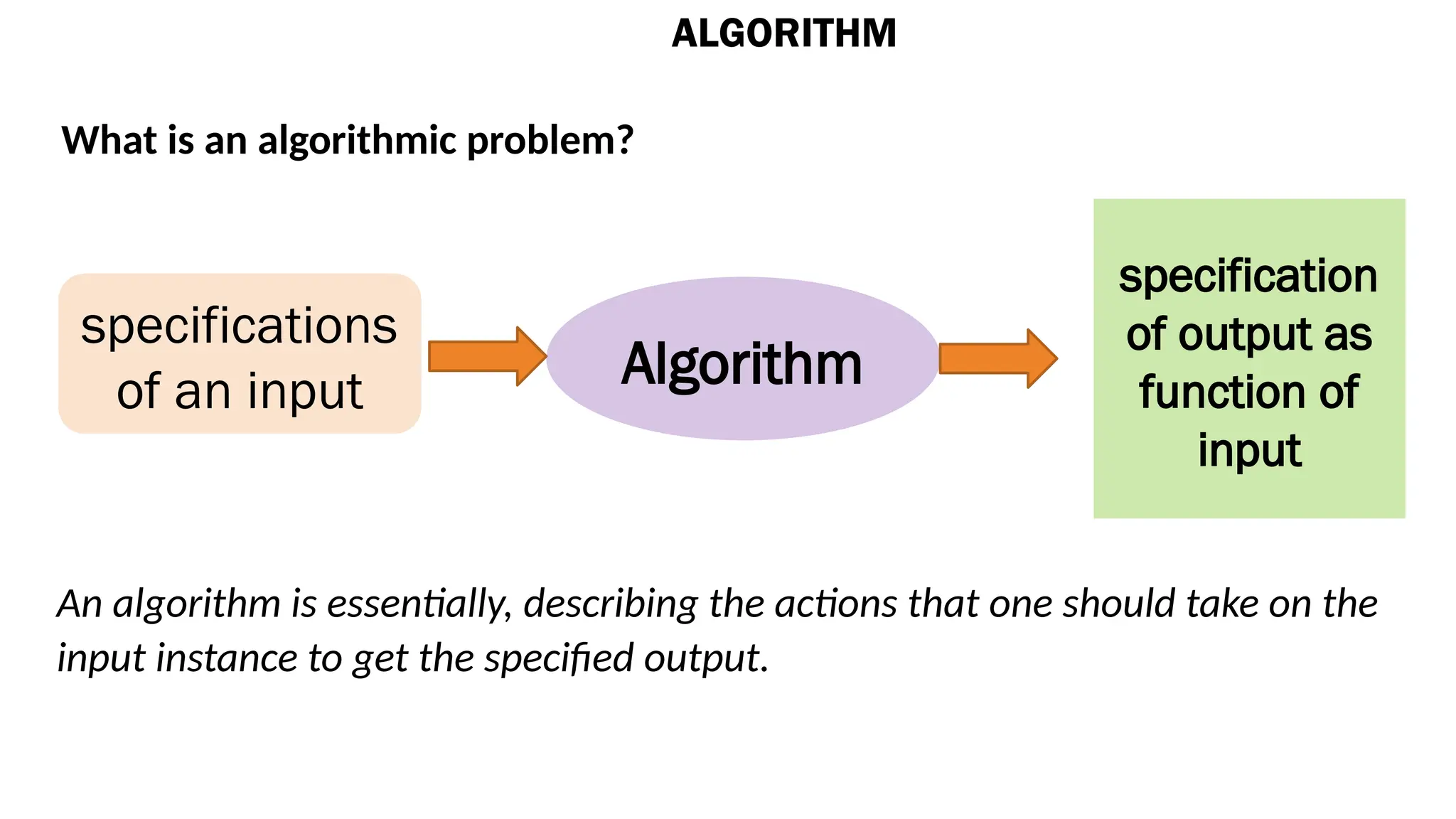
An algorithm is a defined computational procedure that takes input values and produces output values through a sequence of steps. Characteristics of algorithms include unambiguity, defined inputs/outputs, finiteness, feasibility, and independence from programming languages. Analyzing algorithms involves assessing their correctness and efficiency, often considering factors like running time and resource consumption.