Analysis of Algorithms-Heapsort

Analysis of Algorithms
CS 477/677
Heapsort
Instructor: George Bebis
(Chapter 6, Appendix B.5)

2
Special Types of Trees
• Def: Full binary tree = a
binary tree in which each
node is either a leaf or has
degree exactly 2.
• Def: Complete binary tree = a
binary tree in which all leaves
are on the same level and all
internal nodes have degree 2.
Full binary tree
2
14 8
1
16
7
4
3
9 10
12
Complete binary tree
2
1
16
4
3
9 10

3
Definitions
• Height of a node = the number of edges on the longest
simple path from the node down to a leaf
• Level of a node = the length of a path from the root to
the node
• Height of tree = height of root node
2
14 8
1
16
4
3
9 10
Height of root = 3
Height of (2)= 1 Level of (10)= 2

4
Useful Properties
2
14 8
1
16
4
3
9 10
Height of root = 3
Height of (2)= 1 Level of (10)= 2
height
height
1
1
0
2 1
2 2 1
2 1
d
d
l d
l
n




   


(see Ex 6.1-2, page 129)

5
The Heap Data Structure
• Def: A heap is a nearly complete binary tree with
the following two properties:
– Structural property: all levels are full, except
possibly the last one, which is filled from left to right
– Order (heap) property: for any node x
Parent(x) ≥ x
Heap
5
7
8
4
2
From the heap property, it
follows that:
“The root is the maximum
element of the heap!”
A heap is a binary tree that is filled in order

6
Array Representation of Heaps
• A heap can be stored as an
array A.
– Root of tree is A[1]
– Left child of A[i] = A[2i]
– Right child of A[i] = A[2i + 1]
– Parent of A[i] = A[ i/2 ]
– Heapsize[A] ≤ length[A]
• The elements in the subarray
A[(n/2+1) .. n] are leaves

7
Heap Types
• Max-heaps (largest element at root), have the
max-heap property:
– for all nodes i, excluding the root:
A[PARENT(i)] ≥ A[i]
• Min-heaps (smallest element at root), have the
min-heap property:
– for all nodes i, excluding the root:
A[PARENT(i)] ≤ A[i]

8
Adding/Deleting Nodes
• New nodes are always inserted at the bottom
level (left to right)
• Nodes are removed from the bottom level (right
to left)

9
Operations on Heaps
• Maintain/Restore the max-heap property
– MAX-HEAPIFY
• Create a max-heap from an unordered array
– BUILD-MAX-HEAP
• Sort an array in place
– HEAPSORT
• Priority queues

10
Maintaining the Heap Property
• Suppose a node is smaller than a
child
– Left and Right subtrees of i are max-heaps
• To eliminate the violation:
– Exchange with larger child
– Move down the tree
– Continue until node is not smaller than
children

11
Example
MAX-HEAPIFY(A, 2, 10)
A[2] violates the heap property
A[2]  A[4]
A[4] violates the heap property
A[4]  A[9]
Heap property restored

12
Maintaining the Heap Property
• Assumptions:
– Left and Right
subtrees of i are
max-heaps
– A[i] may be
smaller than its
children
Alg: MAX-HEAPIFY(A, i, n)
1. l ← LEFT(i)
2. r ← RIGHT(i)
3. if l ≤ n and A[l] > A[i]
4. then largest ←l
5. else largest ←i
6. if r ≤ n and A[r] > A[largest]
7. then largest ←r
8. if largest  i
9. then exchange A[i] ↔ A[largest]
10. MAX-HEAPIFY(A, largest, n)

13
MAX-HEAPIFY Running Time
• Intuitively:
• Running time of MAX-HEAPIFY is O(lgn)
• Can be written in terms of the height of the heap,
as being O(h)
– Since the height of the heap is lgn
h
2h
O(h)
-
-
-
-

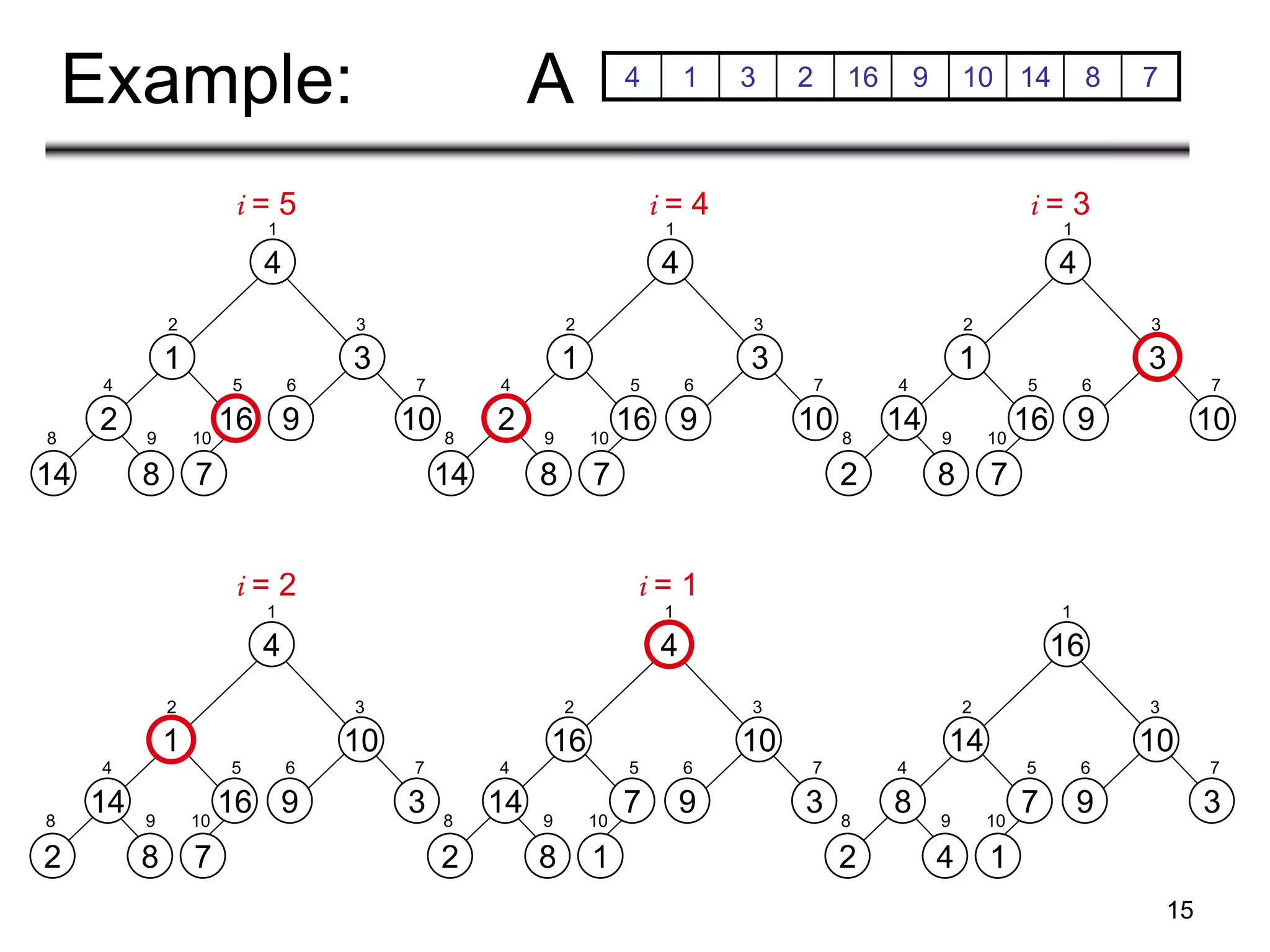
14
Building a Heap
Alg: BUILD-MAX-HEAP(A)
1. n = length[A]
2. for i ← n/2 downto 1
3. do MAX-HEAPIFY(A, i, n)
• Convert an array A[1 … n] into a max-heap (n = length[A])
• The elements in the subarray A[(n/2+1) .. n] are leaves
• Apply MAX-HEAPIFY on elements between 1 and n/2
2
14 8
1
16
7
4
3
9 10
1
2 3
4 5 6 7
8 9 10
4 1 3 2 16 9 10 14 8 7
A:

15
Example: A 4 1 3 2 16 9 10 14 8 7
2
14 8
1
16
7
4
3
9 10
1
2 3
4 5 6 7
8 9 10
14
2 8
1
16
7
4
10
9 3
1
2 3
4 5 6 7
8 9 10
2
14 8
1
16
7
4
3
9 10
1
2 3
4 5 6 7
8 9 10
14
2 8
1
16
7
4
3
9 10
1
2 3
4 5 6 7
8 9 10
14
2 8
16
7
1
4
10
9 3
1
2 3
4 5 6 7
8 9 10
8
2 4
14
7
1
16
10
9 3
1
2 3
4 5 6 7
8 9 10
i = 5 i = 4 i = 3
i = 2 i = 1

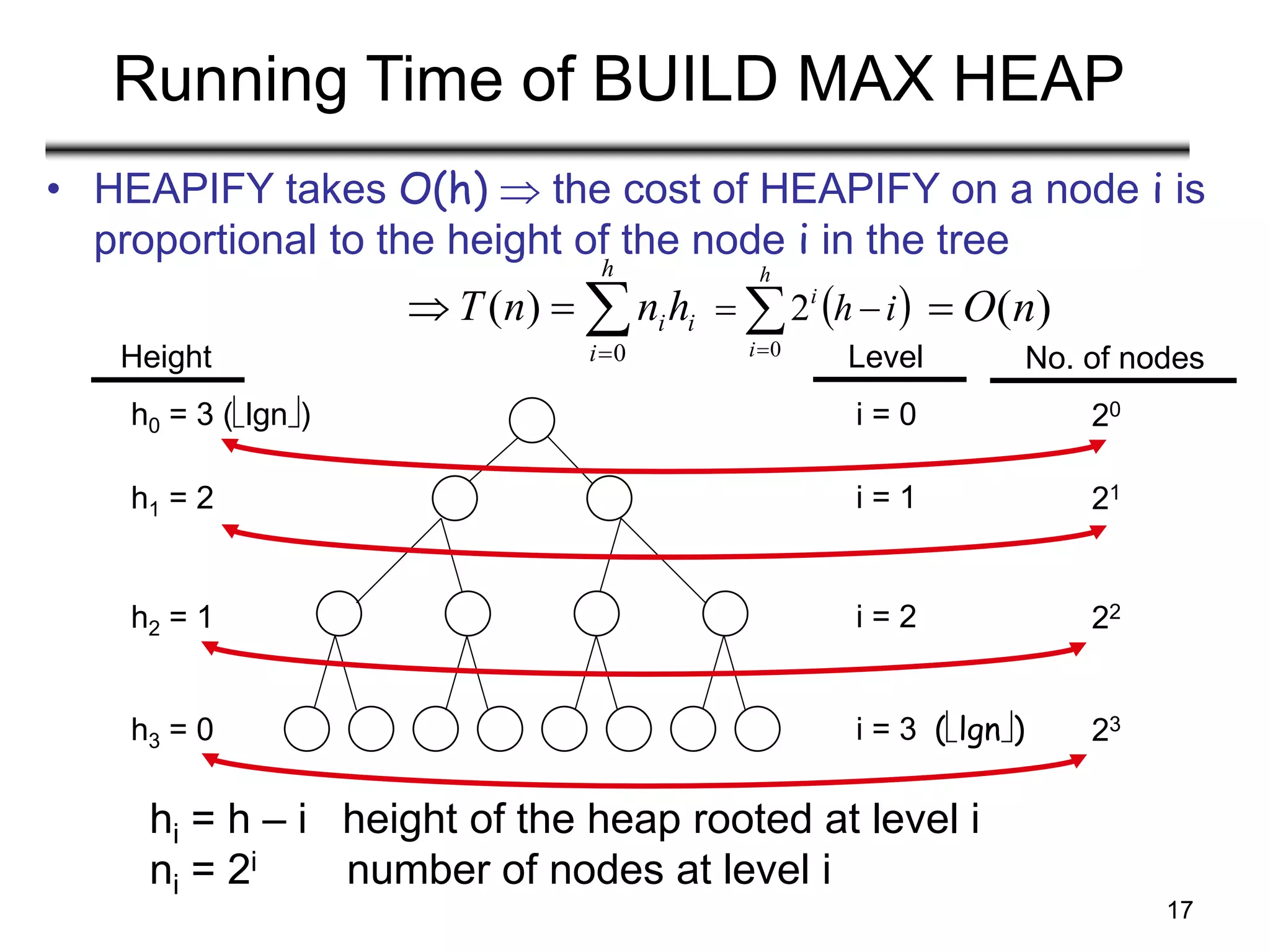
16
Running Time of BUILD MAX HEAP
 Running time: O(nlgn)
• This is not an asymptotically tight upper bound
Alg: BUILD-MAX-HEAP(A)
1. n = length[A]
2. for i ← n/2 downto 1
3. do MAX-HEAPIFY(A, i, n) O(lgn)
O(n)

17
• HEAPIFY takes O(h)  the cost of HEAPIFY on a node i is
proportional to the height of the node i in the tree
Height Level
h0 = 3 (lgn)
h1 = 2
h2 = 1
h3 = 0
i = 0
i = 1
i = 2
i = 3 (lgn)
No. of nodes
20
21
22
23
hi = h – i height of the heap rooted at level i
ni = 2i number of nodes at level i
i
h
i
ih
n
n
T 



0
)
(  
i
h
h
i
i

 
0
2 )
(n
O


18
i
h
i
ih
n
n
T 


0
)
( Cost of HEAPIFY at level i  number of nodes at that level
 
i
h
h
i
i

 
0
2 Replace the values of ni and hi computed before
h
h
i
i
h
i
h
2
2
0




 Multiply by 2h both at the nominator and denominator and
write 2i as i

2
1



h
k
k
h k
0 2
2 Change variables: k = h - i




0 2
k
k
k
n The sum above is smaller than the sum of all elements to 
and h = lgn
)
(n
O
 The sum above is smaller than 2
Running time of BUILD-MAX-HEAP: T(n) = O(n)

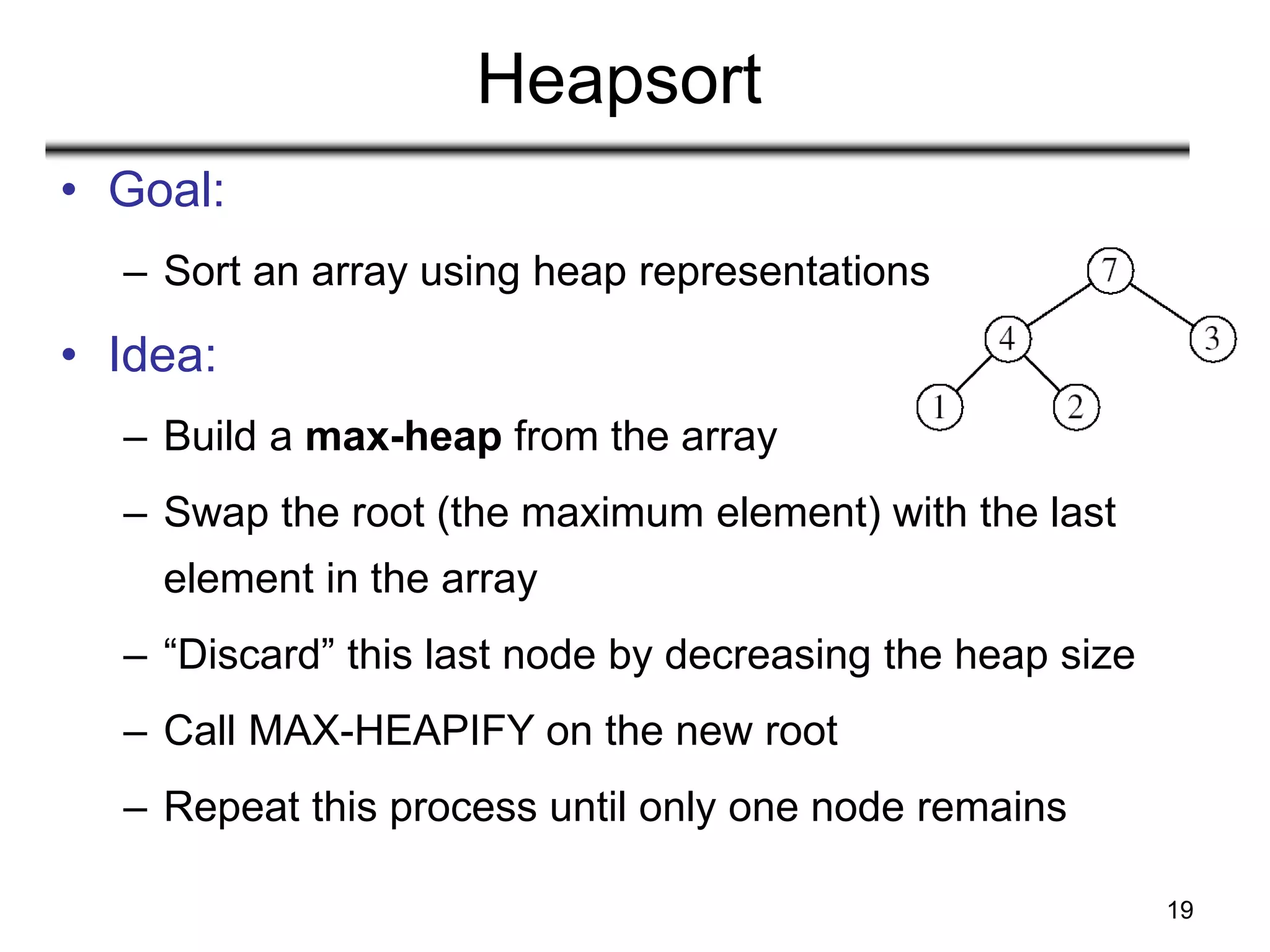
19
Heapsort
• Goal:
– Sort an array using heap representations
• Idea:
– Build a max-heap from the array
– Swap the root (the maximum element) with the last
element in the array
– “Discard” this last node by decreasing the heap size
– Call MAX-HEAPIFY on the new root
– Repeat this process until only one node remains

20
Example: A=[7, 4, 3, 1, 2]
MAX-HEAPIFY(A, 1, 4) MAX-HEAPIFY(A, 1, 3) MAX-HEAPIFY(A, 1, 2)
MAX-HEAPIFY(A, 1, 1)

21
Alg: HEAPSORT(A)
1. BUILD-MAX-HEAP(A)
2. for i ← length[A] downto 2
3. do exchange A[1] ↔ A[i]
4. MAX-HEAPIFY(A, 1, i - 1)
• Running time: O(nlgn) --- Can be
shown to be Θ(nlgn)
O(n)
O(lgn)
n-1 times

23
Operations
on Priority Queues
• Max-priority queues support the following
operations:
– INSERT(S, x): inserts element x into set S
– EXTRACT-MAX(S): removes and returns element of
S with largest key
– MAXIMUM(S): returns element of S with largest key
– INCREASE-KEY(S, x, k): increases value of element
x’s key to k (Assume k ≥ x’s current key value)

24
HEAP-MAXIMUM
Goal:
– Return the largest element of the heap
Alg: HEAP-MAXIMUM(A)
1. return A[1]
Running time: O(1)
Heap A:
Heap-Maximum(A) returns 7

25
HEAP-EXTRACT-MAX
Goal:
– Extract the largest element of the heap (i.e., return the max
value and also remove that element from the heap
Idea:
– Exchange the root element with the last
– Decrease the size of the heap by 1 element
– Call MAX-HEAPIFY on the new root, on a heap of size n-1
Heap A: Root is the largest element

26
Example: HEAP-EXTRACT-MAX
8
2 4
14
7
1
16
10
9 3
max = 16
8
2 4
14
7
1
10
9 3
Heap size decreased with 1
4
2 1
8
7
14
10
9 3
Call MAX-HEAPIFY(A, 1, n-1)

27
HEAP-EXTRACT-MAX
Alg: HEAP-EXTRACT-MAX(A, n)
1. if n < 1
2. then error “heap underflow”
3. max ← A[1]
4. A[1] ← A[n]
5. MAX-HEAPIFY(A, 1, n-1) remakes heap
6. return max
Running time: O(lgn)

28
HEAP-INCREASE-KEY
• Goal:
– Increases the key of an element i in the heap
• Idea:
– Increment the key of A[i] to its new value
– If the max-heap property does not hold anymore:
traverse a path toward the root to find the proper
place for the newly increased key
8
2 4
14
7
1
16
10
9 3
i
Key [i] ← 15

29
Example: HEAP-INCREASE-KEY
14
2 8
15
7
1
16
10
9 3
i
8
2 4
14
7
1
16
10
9 3
i
Key [i ] ← 15
8
2 15
14
7
1
16
10
9 3
i
15
2 8
14
7
1
16
10
9 3
i

30
HEAP-INCREASE-KEY
Alg: HEAP-INCREASE-KEY(A, i, key)
1. if key < A[i]
2. then error “new key is smaller than current key”
3. A[i] ← key
4. while i > 1 and A[PARENT(i)] < A[i]
5. do exchange A[i] ↔ A[PARENT(i)]
6. i ← PARENT(i)
• Running time: O(lgn)
8
2 4
14
7
1
16
10
9 3
i
Key [i] ← 15

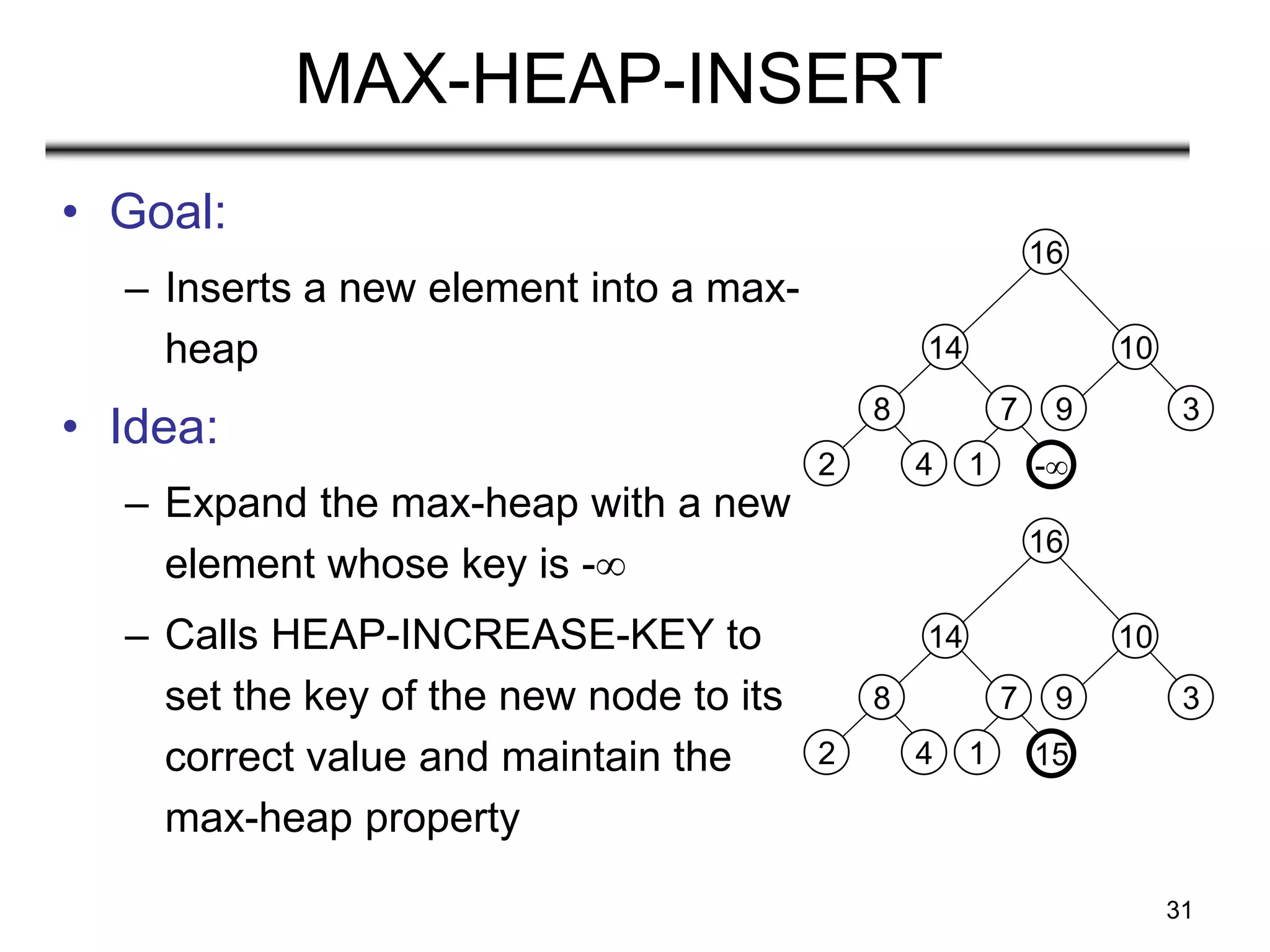
31
-
MAX-HEAP-INSERT
• Goal:
– Inserts a new element into a max-
heap
• Idea:
– Expand the max-heap with a new
element whose key is -
– Calls HEAP-INCREASE-KEY to
set the key of the new node to its
correct value and maintain the
max-heap property
8
2 4
14
7
1
16
10
9 3
15
8
2 4
14
7
1
16
10
9 3

32
Example: MAX-HEAP-INSERT
-
8
2 4
14
7
1
16
10
9 3
Insert value 15:
- Start by inserting -
15
8
2 4
14
7
1
16
10
9 3
Increase the key to 15
Call HEAP-INCREASE-KEY on A[11] = 15
7
8
2 4
14
15
1
16
10
9 3
7
8
2 4
15
14
1
16
10
9 3
The restored heap containing
the newly added element

33
MAX-HEAP-INSERT
Alg: MAX-HEAP-INSERT(A, key, n)
1. heap-size[A] ← n + 1
2. A[n + 1] ← -
3. HEAP-INCREASE-KEY(A, n + 1, key)
Running time: O(lgn)
-
8
2 4
14
7
1
16
10
9 3

34
Summary
• We can perform the following operations on
heaps:
– MAX-HEAPIFY O(lgn)
– BUILD-MAX-HEAP O(n)
– HEAP-SORT O(nlgn)
– MAX-HEAP-INSERT O(lgn)
– HEAP-EXTRACT-MAX O(lgn)
– HEAP-INCREASE-KEY O(lgn)
– HEAP-MAXIMUM O(1)
Average
O(lgn)

35
Priority Queue Using Linked List
Average: O(n)
Increase key: O(n)
Extract max key: O(1)
12 4

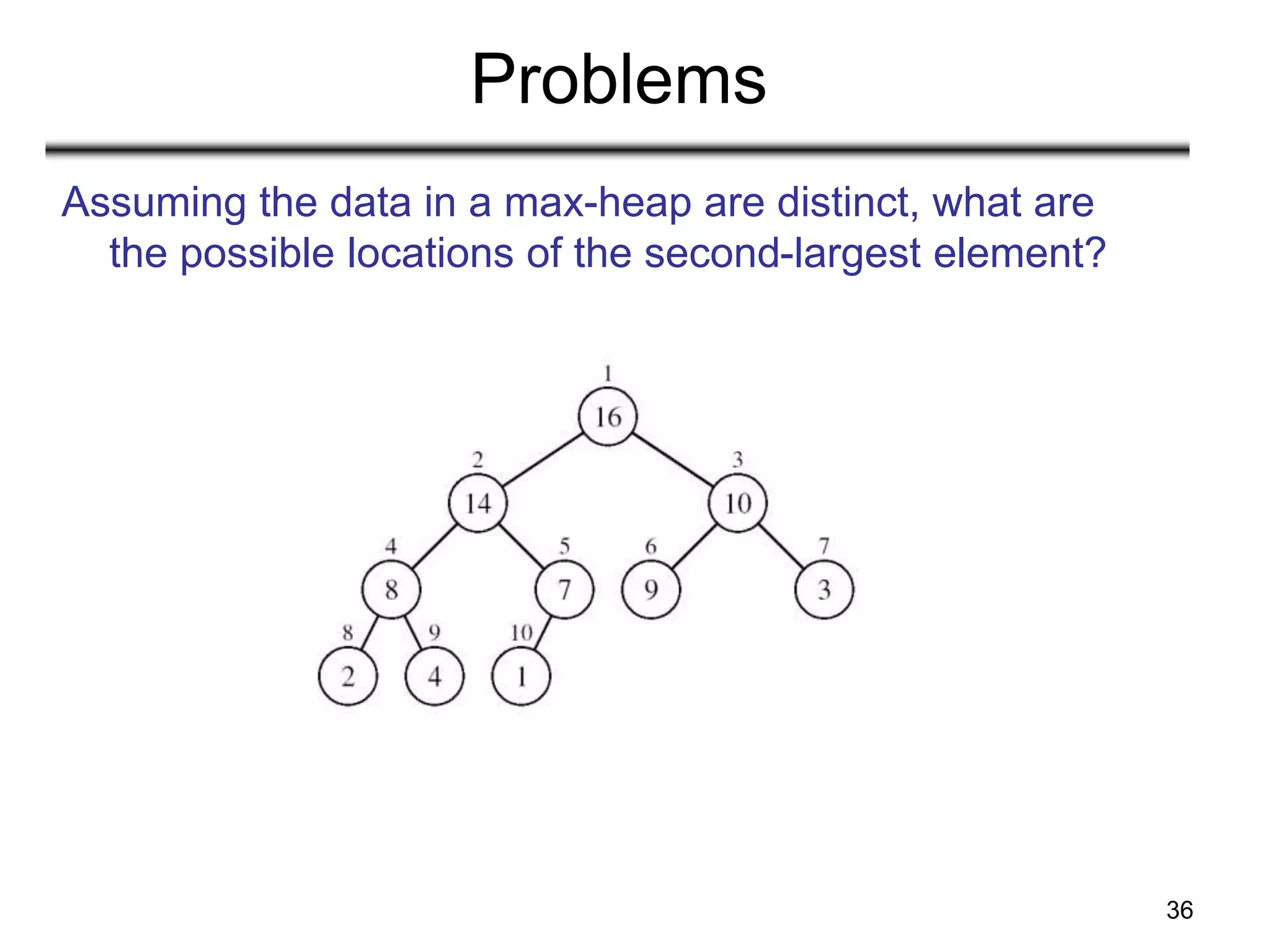
36
Problems
Assuming the data in a max-heap are distinct, what are
the possible locations of the second-largest element?

37
Problems
(a) What is the maximum number of nodes in a
max heap of height h?
(b) What is the maximum number of leaves?
(c) What is the maximum number of internal
nodes?

38
Problems
• Demonstrate, step by step, the operation of
Build-Heap on the array
A=[5, 3, 17, 10, 84, 19, 6, 22, 9]

39
Problems
• Let A be a heap of size n. Give the most
efficient algorithm for the following tasks:
(a) Find the sum of all elements
(b) Find the sum of the largest lgn elements

Analysis of Algorithms-Heapsort

More Related Content

What's hot

Similar to Analysis of Algorithms-Heapsort

More from Reetesh Gupta

Recently uploaded

Analysis of Algorithms-Heapsort