The document discusses applicative style programming, explaining what applicatives are, how they differ from monads, and when to use them. It provides examples and comparisons of monadic and applicative validation, demonstrates how to implement free applicatives, and highlights the advantages of static analysis enabled by applicatives. The talk also covers practical applications of applicatives in various libraries and the potential for performance optimization.







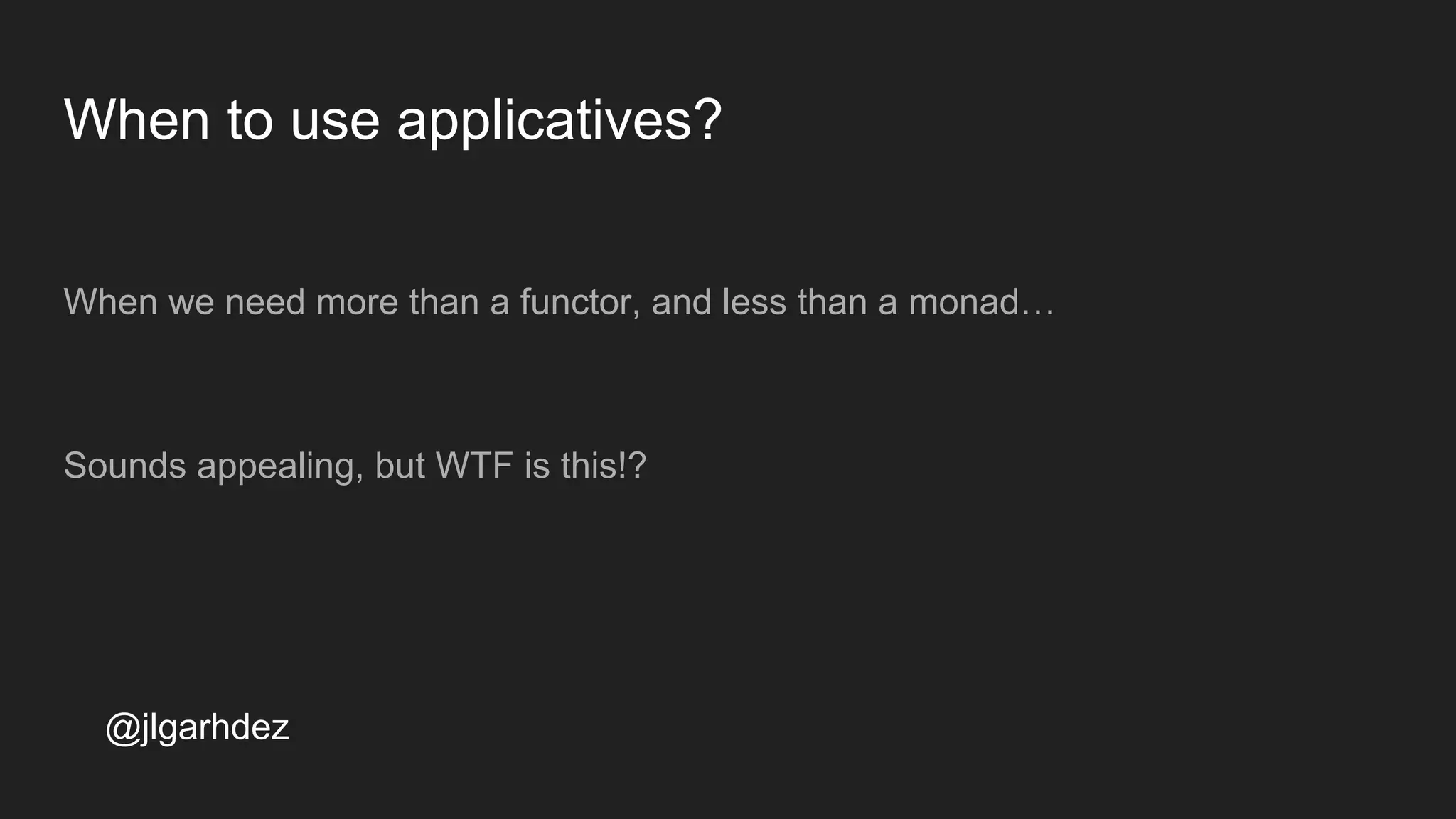
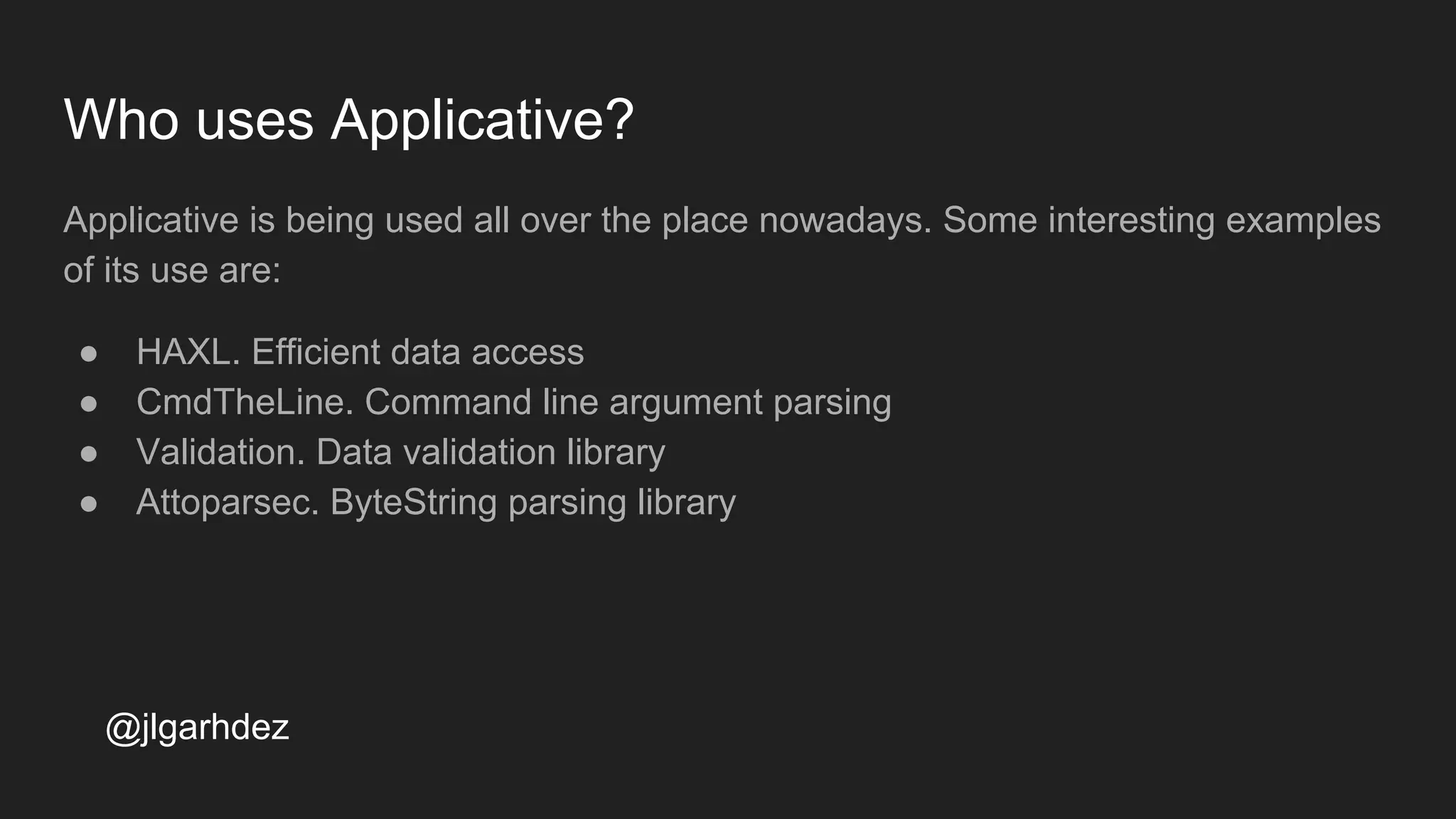
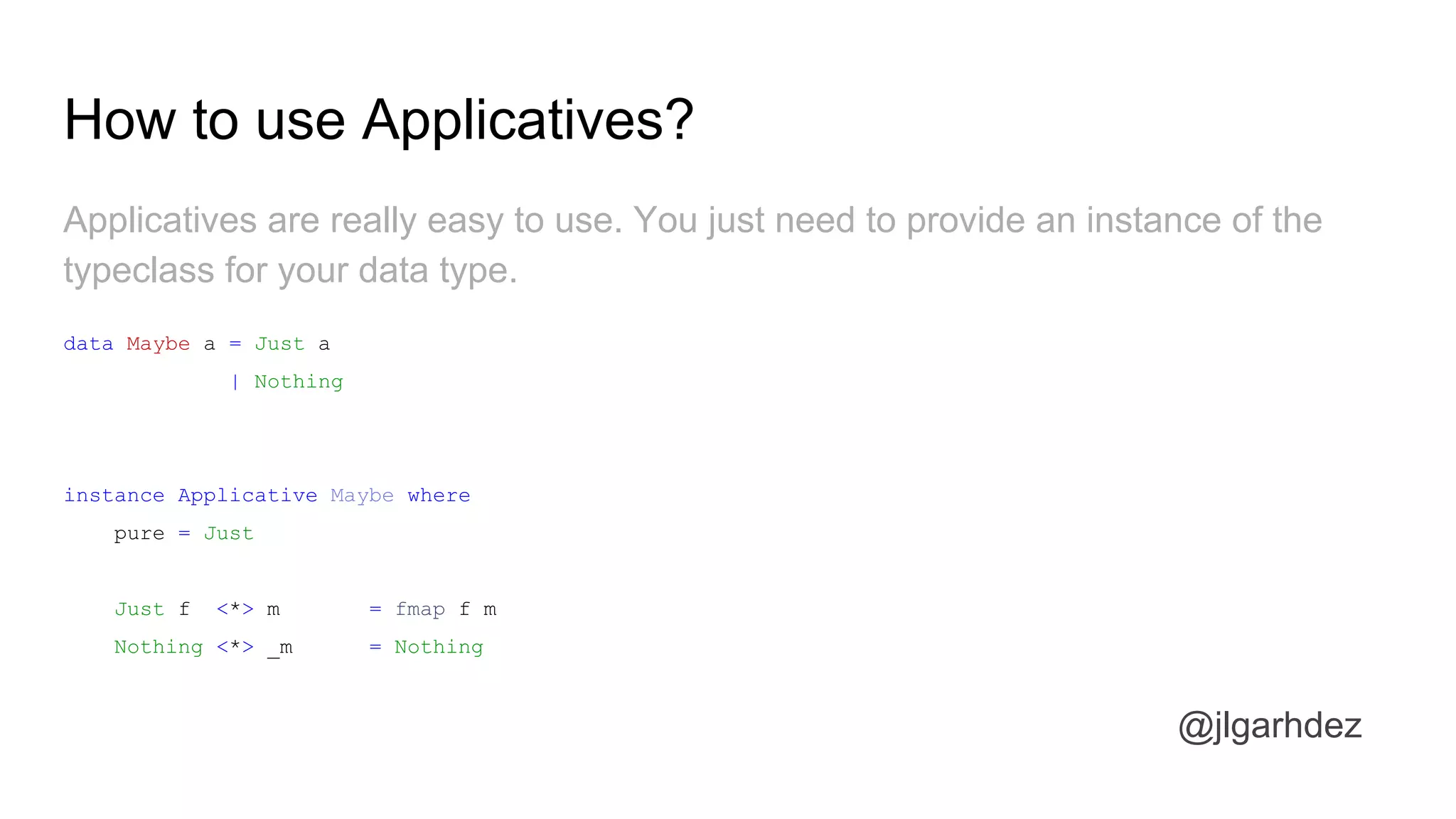
![What are applicatives?
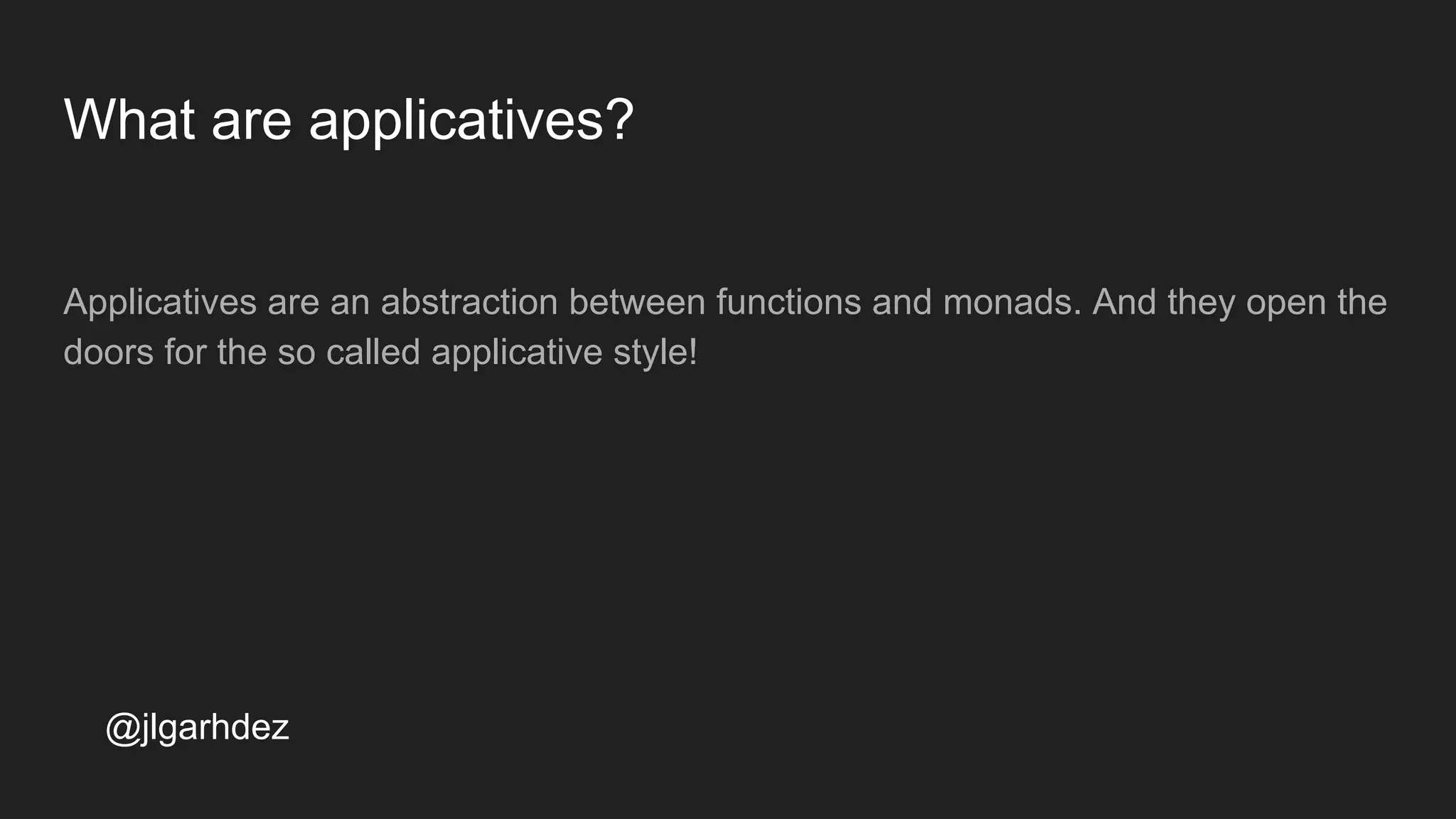
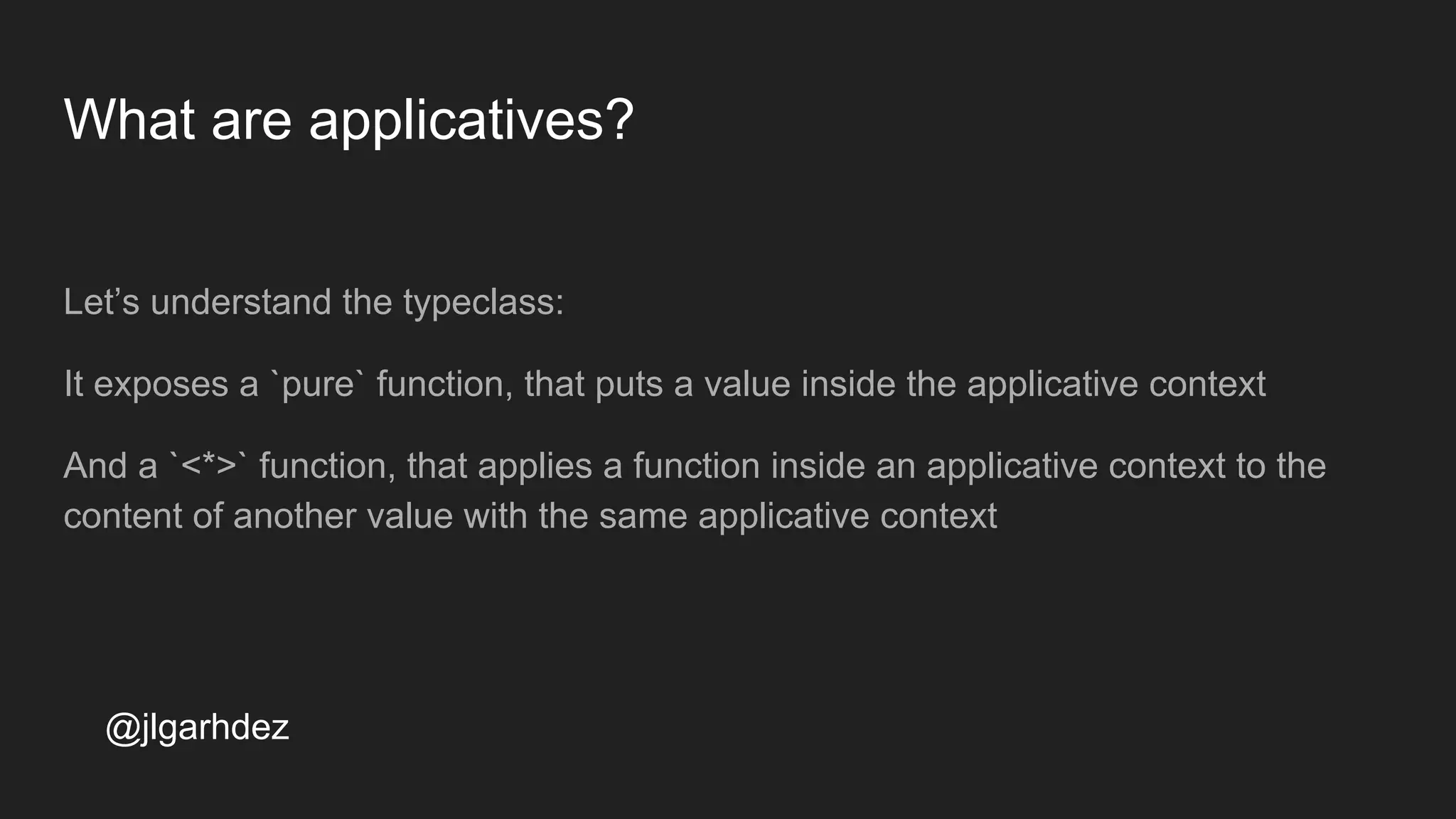
Basically an Applicative is a Functor that can also apply a function contained in a
container to other container of the same type.
Prelude Control.Monad> let fn1 = x-> x * x
Prelude Control.Monad> let fn2 = x -> x + 33
Prelude Control.Monad> let fns = [fn1, fn2]
Prelude Control.Monad> :t fns
fns :: Num a => [a -> a]
Prelude Control.Monad> let nums = [1,2,3,4]
Prelude Control.Monad> :t nums
nums :: Num t => [t]
Prelude Control.Monad> fns <*> nums
jlgarhdez HaskellMADpepegar](https://image.slidesharecdn.com/applicativestyleprogramming-160914224841/75/Applicative-style-programming-10-2048.jpg)



























![Static Analysis
@jlgarhdez
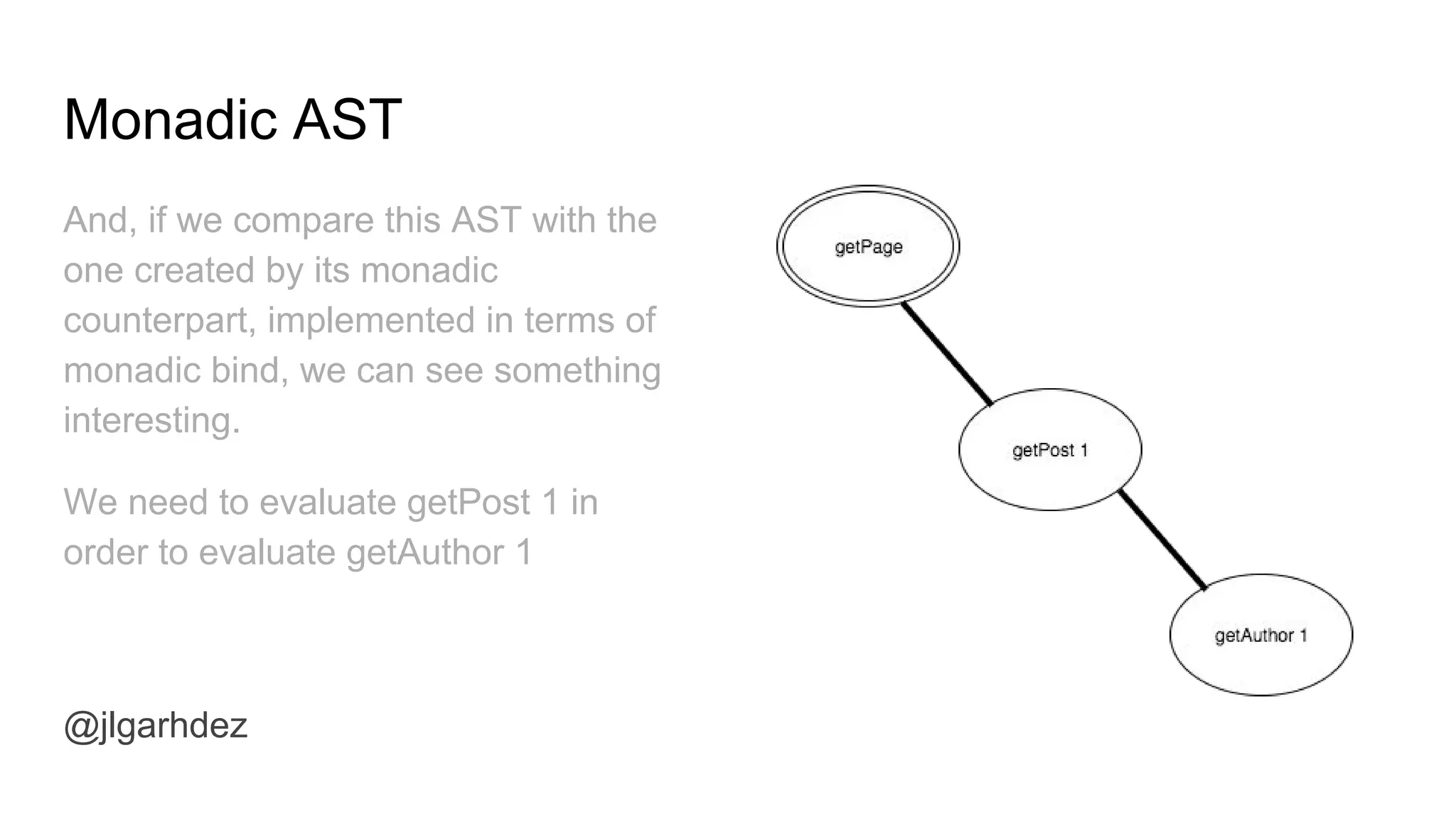
To demonstrate static analysis, let’s keep with our blog example:
data BlogF a where
GetPost :: Id -> BlogF Post
GetAuthor :: Id -> BlogF Author
GetComments :: Id -> BlogF [(Comment, Author)]
type Blog a = Ap BlogF a
jlgarhdez HaskellMADpepegar](https://image.slidesharecdn.com/applicativestyleprogramming-160914224841/75/Applicative-style-programming-45-2048.jpg)
![Static Analysis
@jlgarhdez
Also some convenience functions:
getPost :: Id -> Blog Post
getPost id = liftAp $ GetPost id
getAuthor :: Id -> Blog Author
getAuthor id = liftAp $ GetAuthor id
getComments :: Id -> Blog [(Comment, Author)]
getComments id = liftAp $ GetComments id
jlgarhdez HaskellMADpepegar](https://image.slidesharecdn.com/applicativestyleprogramming-160914224841/75/Applicative-style-programming-46-2048.jpg)

![Static Analysis
@jlgarhdez
And, as explained before, we will need to interpret the AST
interpIO :: BlogF a -> IO a
interpIO (GetPost id) = putStrLn ("getting post " ++ show id ++ " from DB") *> pure "this is the
post"
interpIO (GetAuthor id) = putStrLn ("getting author " ++ show id ++ " from DB") *> pure "@pepe"
interpIO (GetComments id) = putStrLn ("getting comments for post " ++ show id ++ " from DB")
*> pure [
("this post rocks" , "@anler"),
("you're right, @anler" , "@lorenzo"),
("Oh boy, I love haskell so bad!" , "@dani"),
("Indeed, Haskell is better than Erlang!" , "@joseluis" )
]
jlgarhdez HaskellMADpepegar](https://image.slidesharecdn.com/applicativestyleprogramming-160914224841/75/Applicative-style-programming-48-2048.jpg)










