Download as PDF, PPTX
![The answer to the above question will be:
• Solution: [A, B, C, D, G, E, H, F, K, I, L, J, M, N]
• Costs: 13 (there are 13 nodes to step to reach the end node from
the start node)](https://image.slidesharecdn.com/bfsinai-241211064038-59a2344e/85/Breadth-first-search-is-a-graph-traversal-algorithm-25-320.jpg)
![The answer to the above question will be:
• Solution: [A, B, C, D, G, E, H, F, K, I, L, J, M, N]
• Costs: 13 (there are 13 nodes to step to reach the end node from
the start node)](https://image.slidesharecdn.com/bfsinai-241211064038-59a2344e/75/Breadth-first-search-is-a-graph-traversal-algorithm-25-2048.jpg)
Uploaded byHitesh Mohapatra
Breadth-first search is a graph traversal algorithm
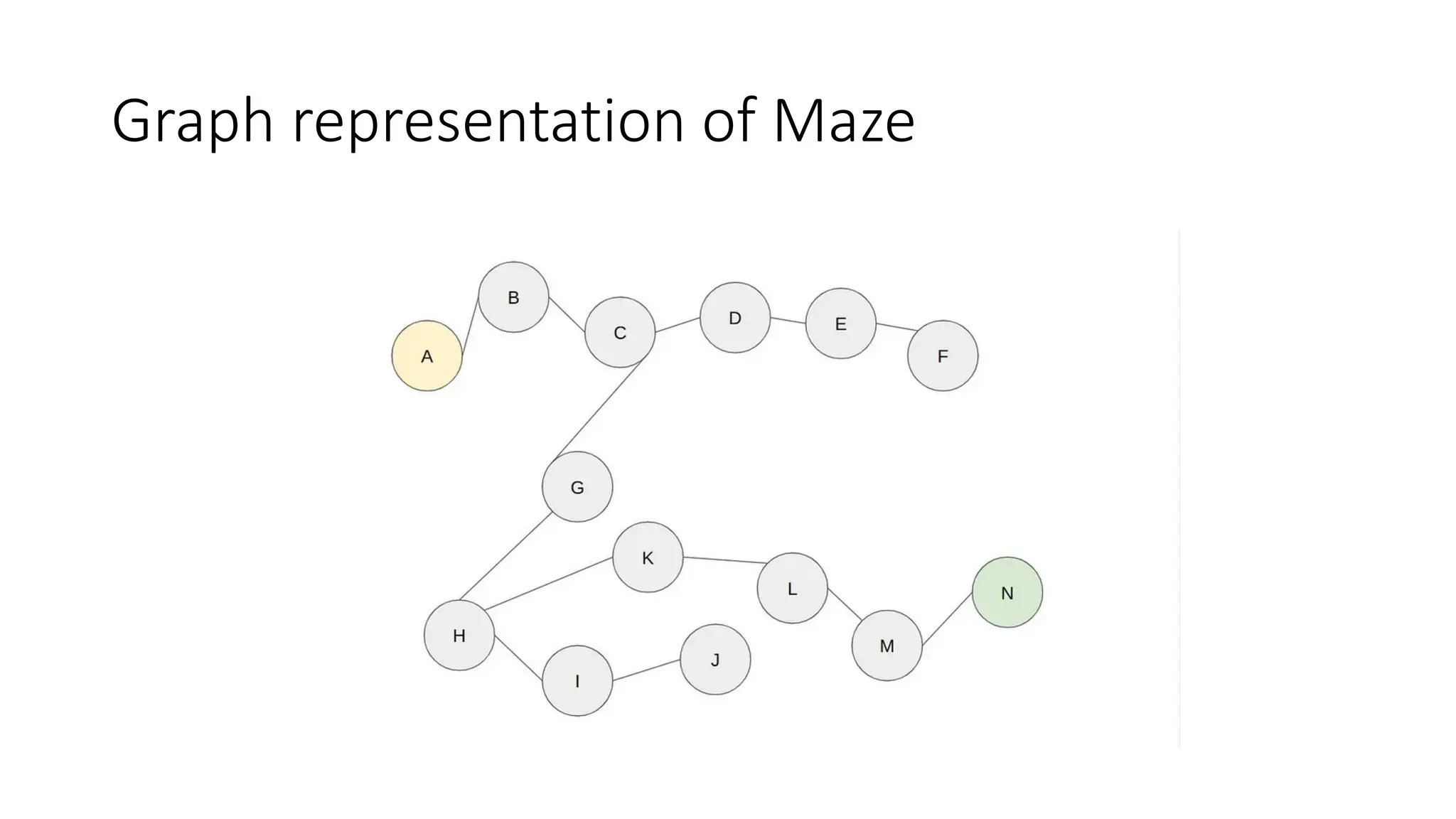
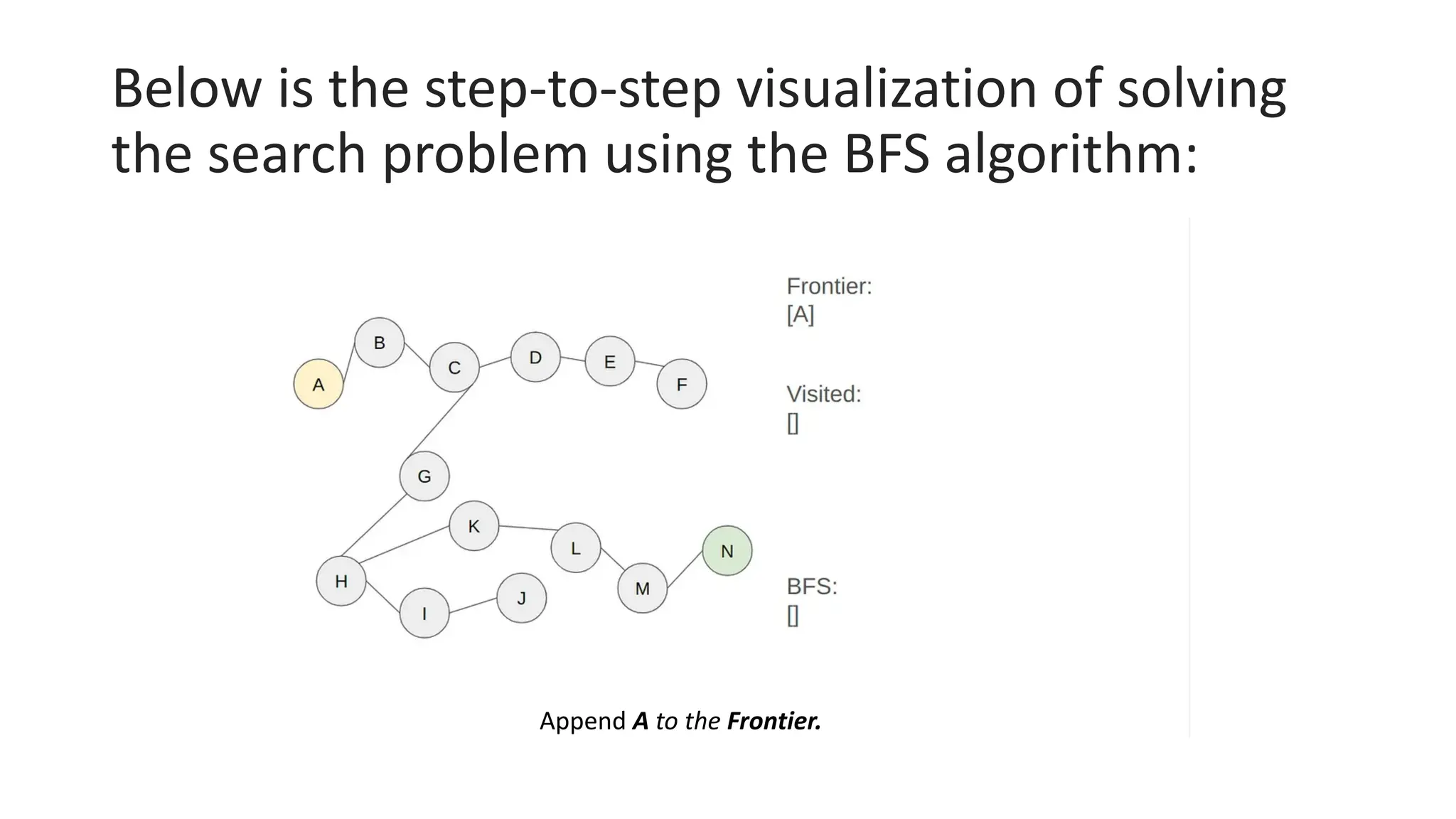
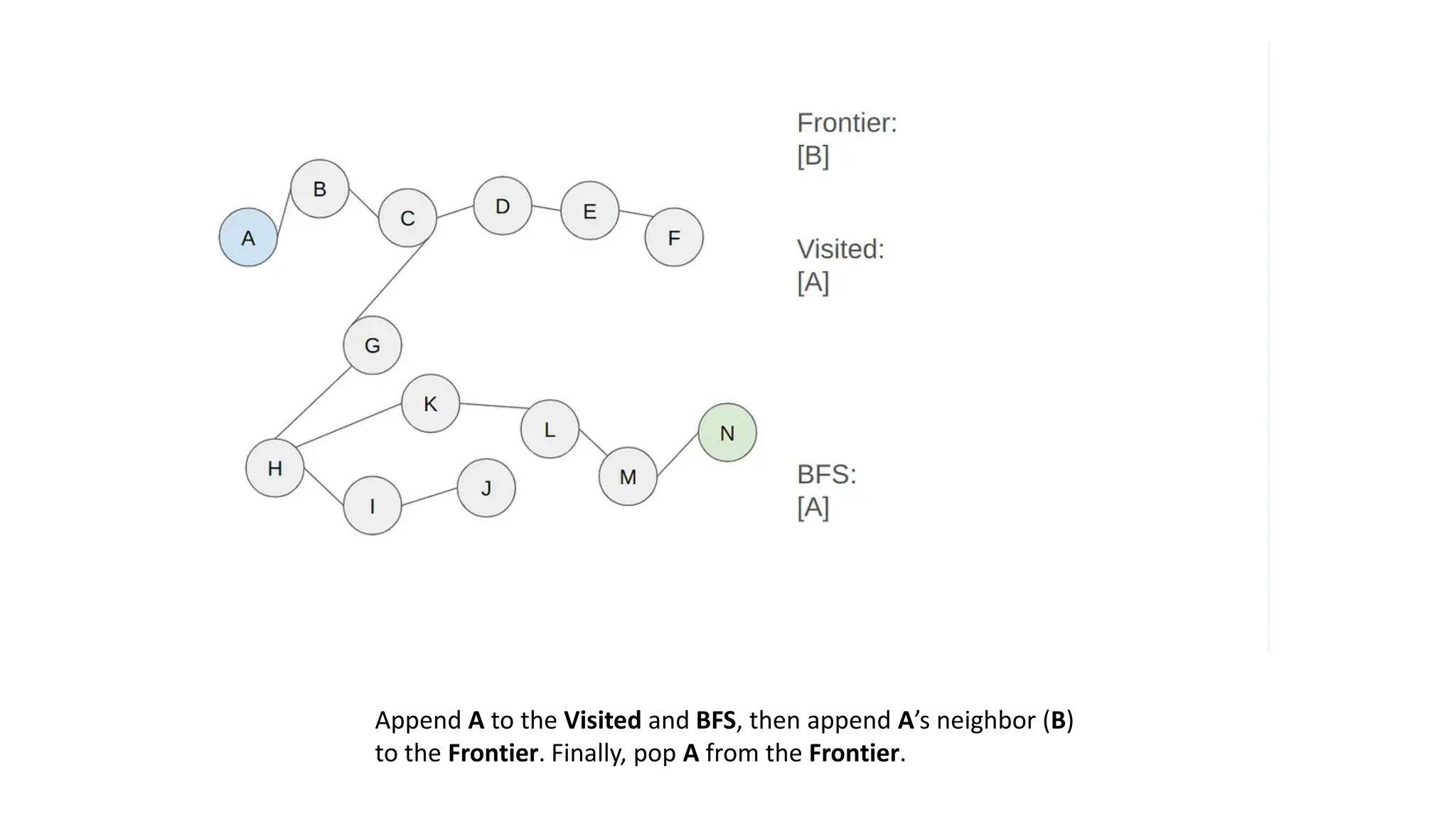
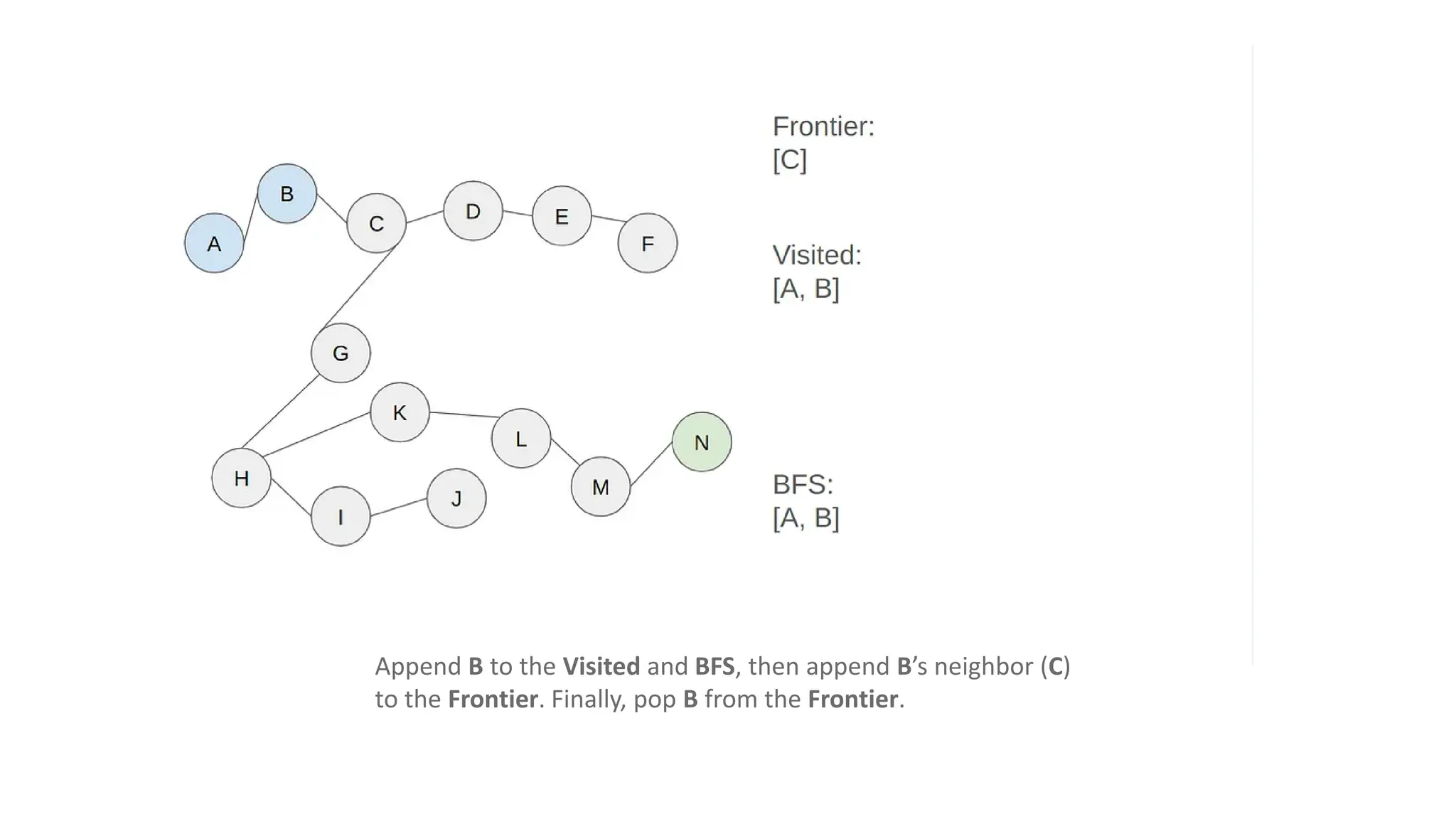
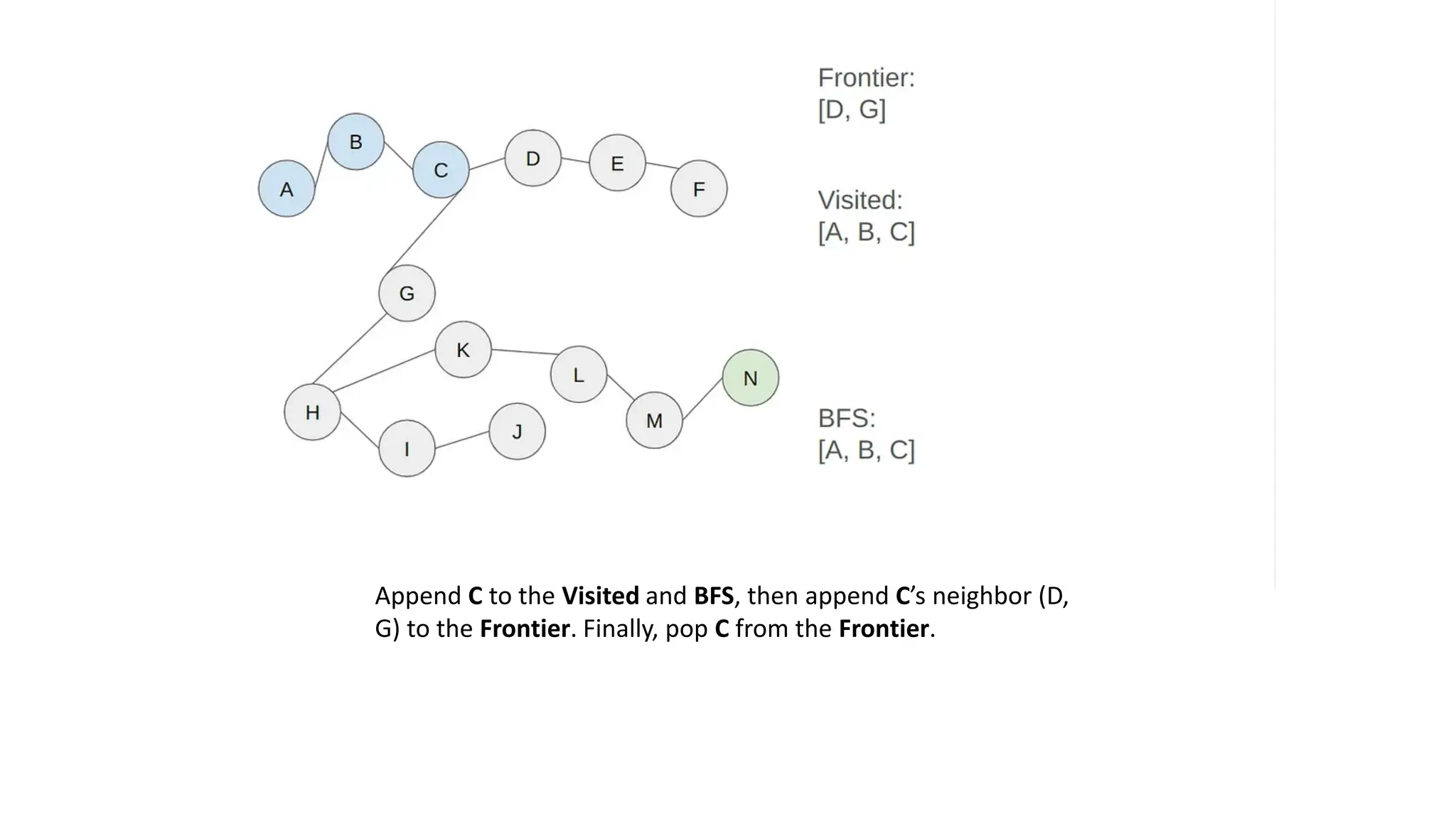
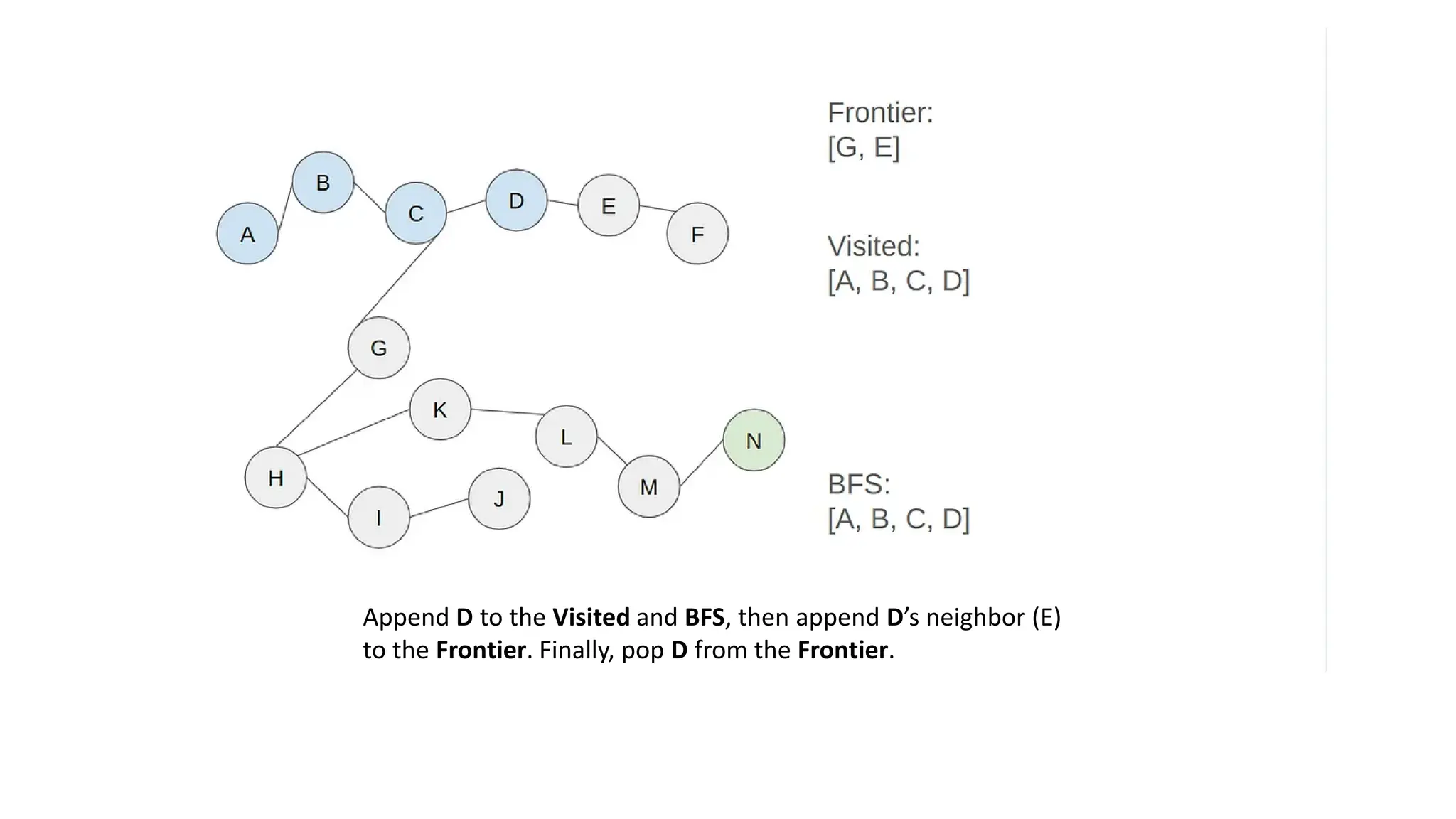
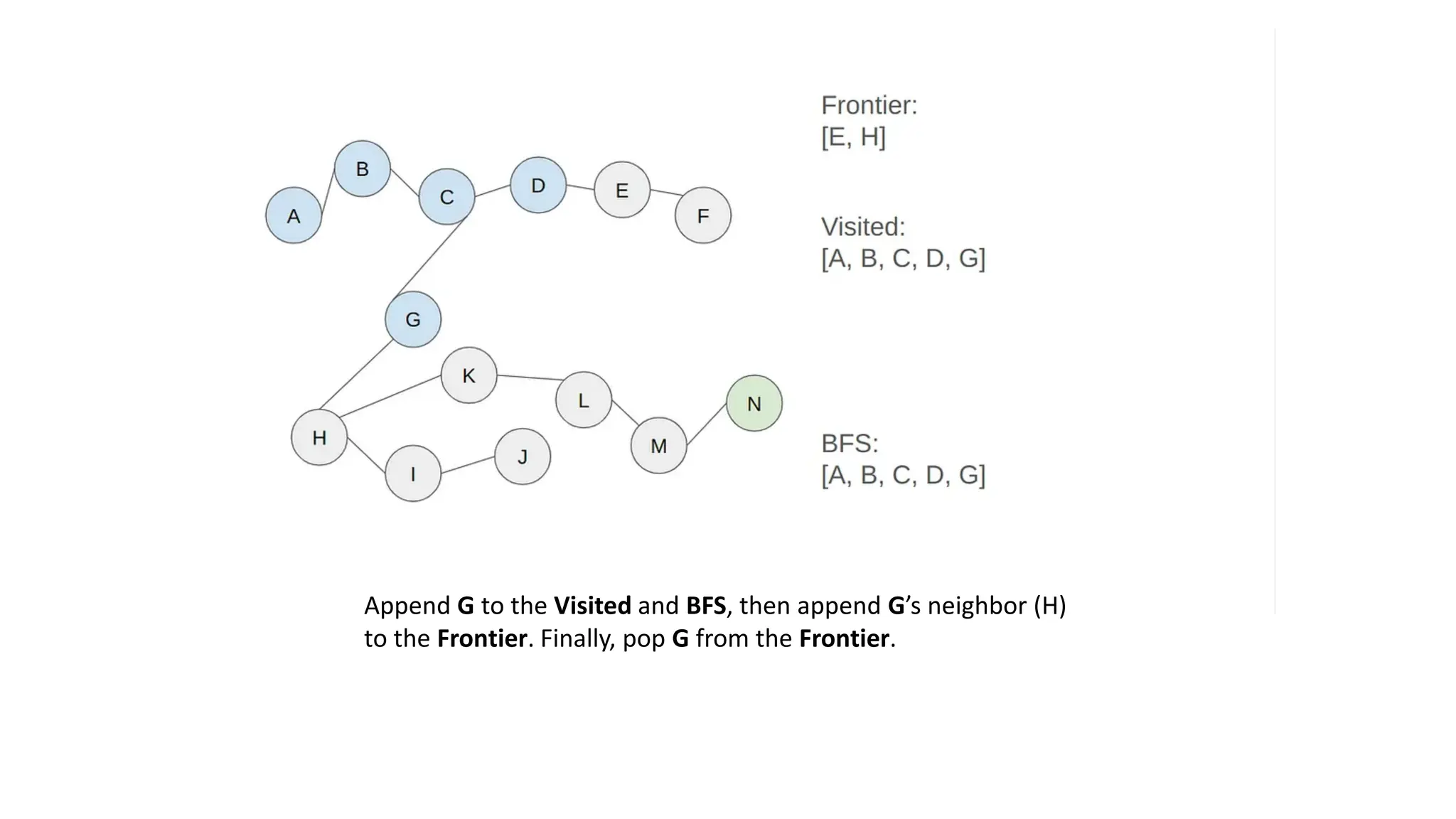
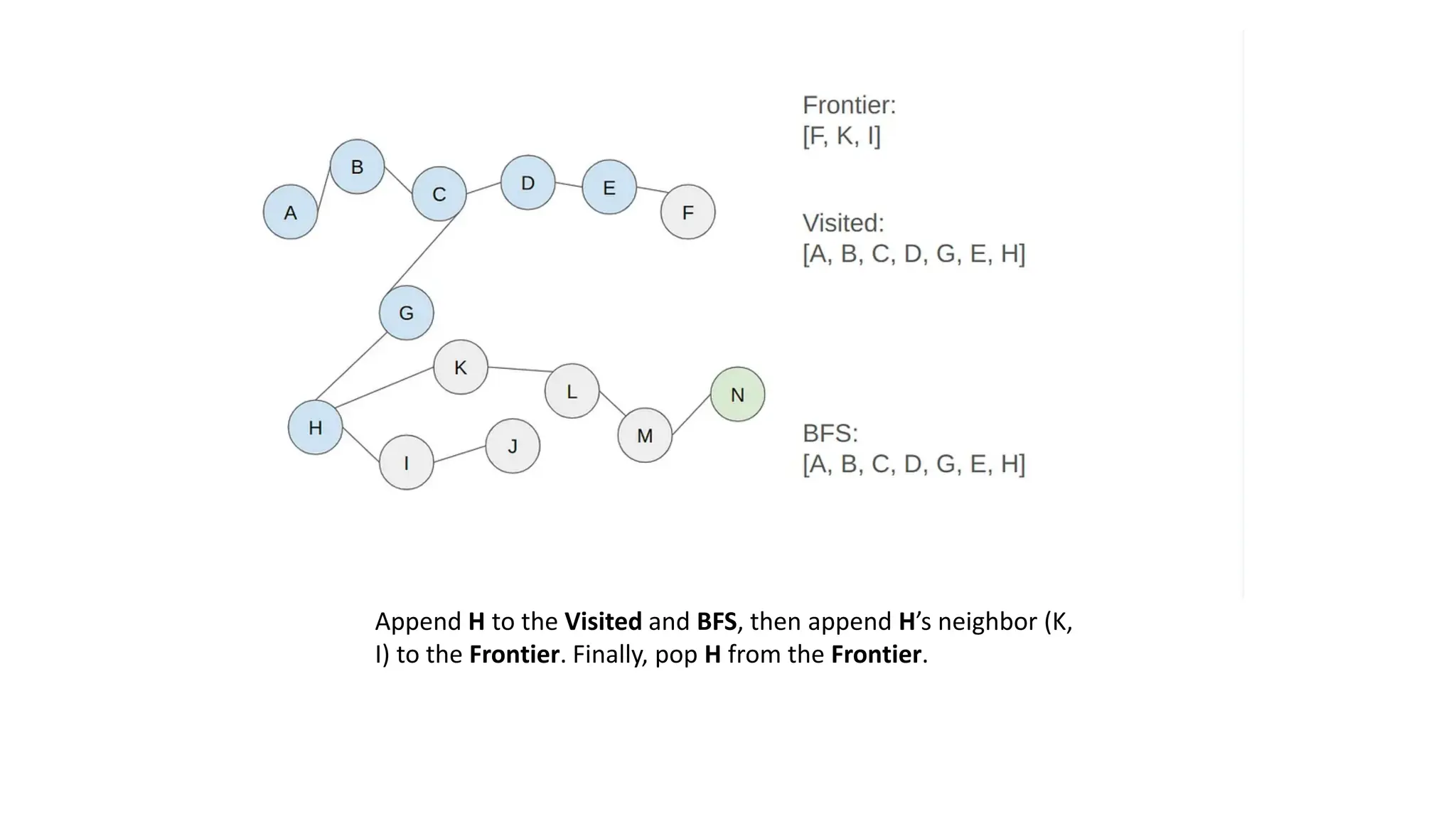
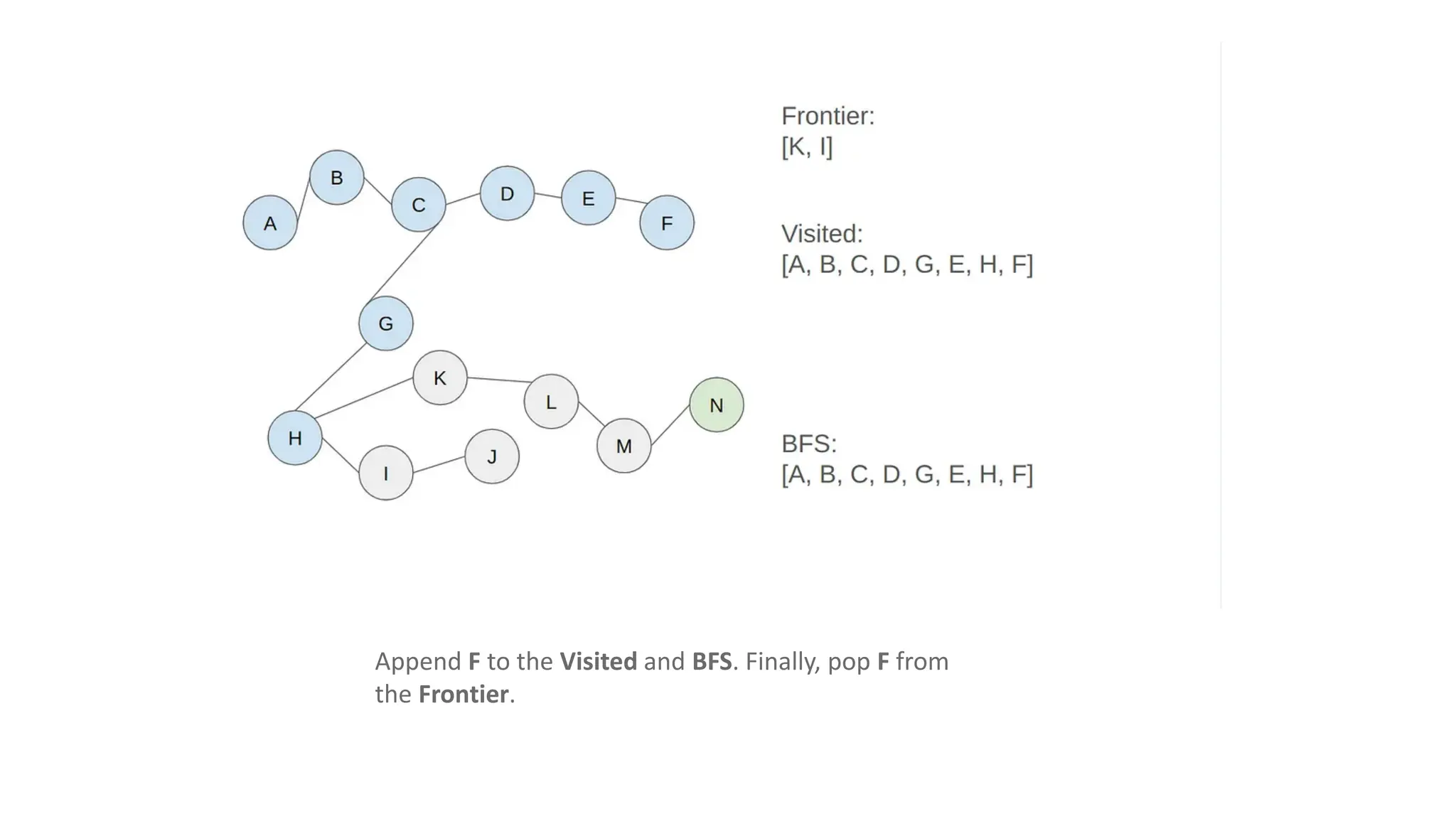
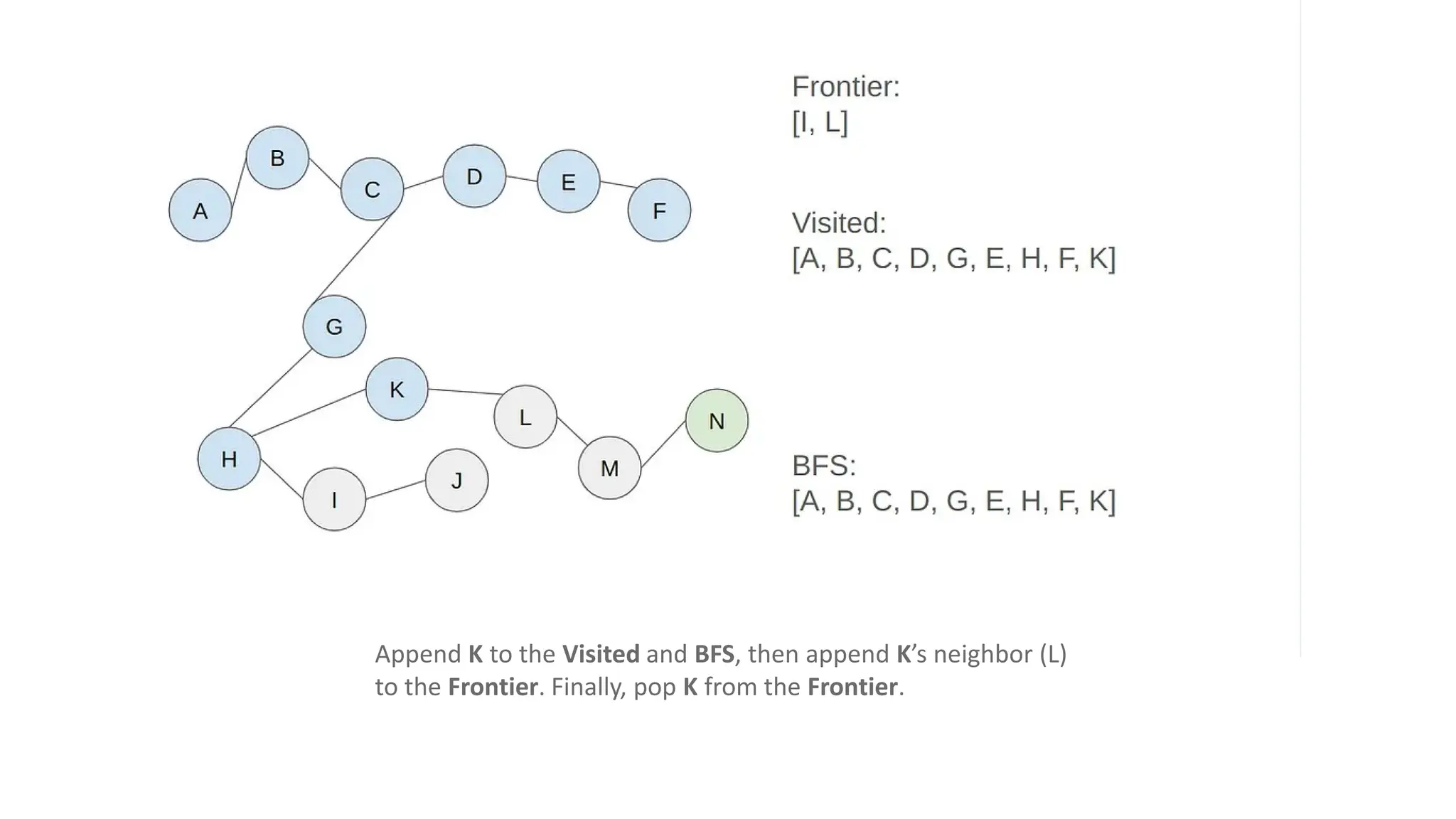
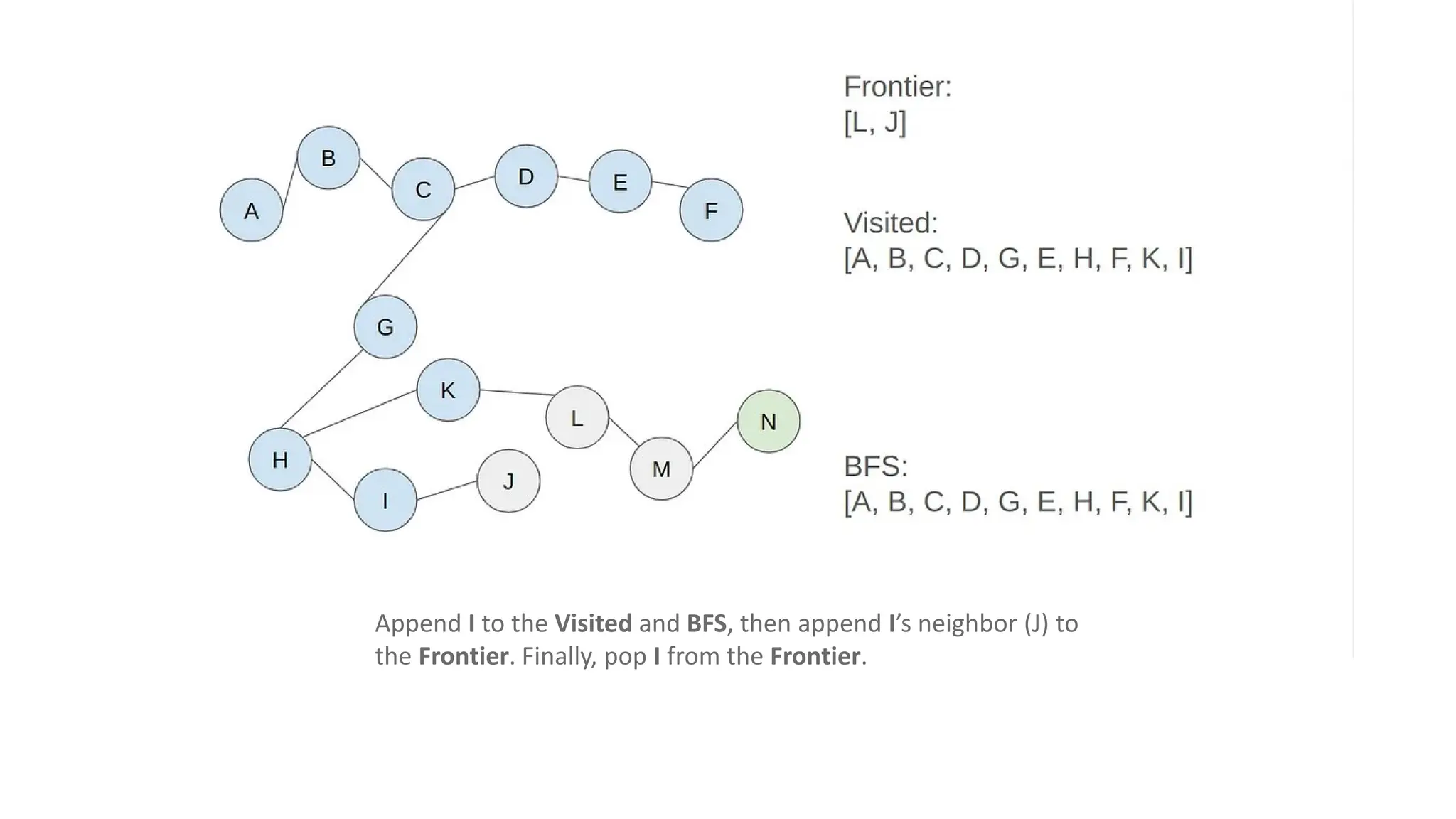
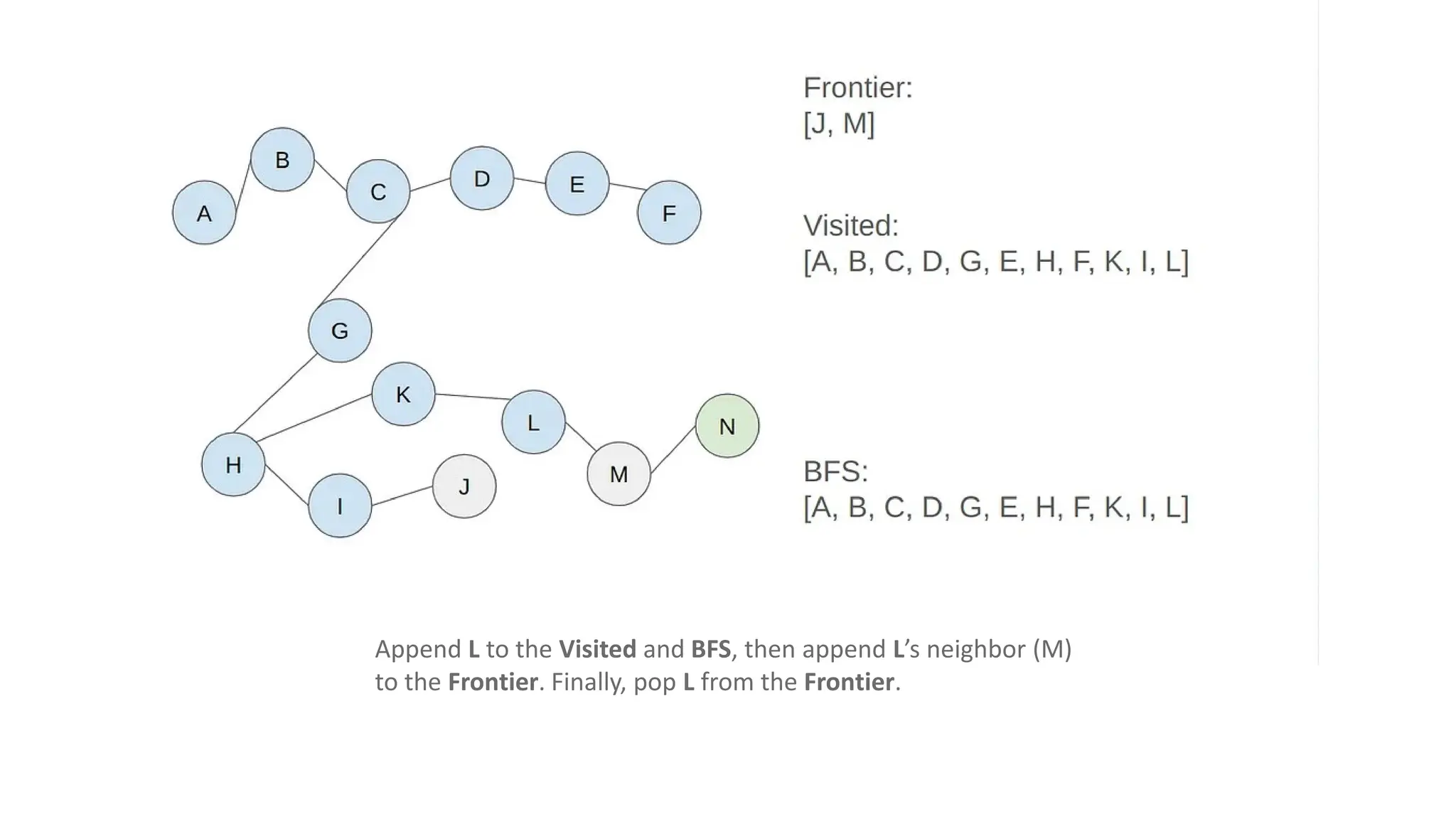
The document outlines an assignment on implementing breadth-first search (BFS) and depth-first search (DFS) algorithms to solve a maze problem, identifying the shortest path and exploring all possible paths. It details the concepts of state space, start state, goal state, and provides a pseudocode for the BFS algorithm along with a step-by-step maze solution example. The final output of the BFS solution shows a path from the start node 'a' to the end node 'n', with a total cost of 13 nodes explored.
More Related Content
Similar to Breadth-first search is a graph traversal algorithm
Breadth-first search is a graph traversal algorithm
- 1. BFS in AI LabAssignment 1 Dr. Hitesh Mohapatra Associate Professor School of Computer Engineering KIIT Deemed to be University
- 2. Assignment-1: Maze Solverusing BFS and DFS Objective: Implement BFS and DFS to solve a maze. Problem Statement: Given a grid-based maze where 0 represents walls and 1 represents walkable paths, find the shortest path from a start cell to an end cell. Tasks: • Use BFS to find the shortest path. • Use DFS to explore all possible paths and report one valid path (not necessarily the shortest). • Compare the number of nodes explored by BFS and DFS.
- 3. AI Search Artificial Intelligencecan be referred to as an agent that can act rationally, it can perform some kind of search algorithm to achieve its tasks in solving a search problem such as a Maze problem.
- 4. A search problemin Artificial Intelligence consists of: • State Space refers to all possible states where the agent can be. • Start State refers to the state where the search begins. • Goal State refers to the state where the search ends. • Solution refers to the sequence of actions that shows how an agent searches from the start state to the goal state. • Cost refers to the effort of the agent in doing the searching task.
- 5. There are severalalgorithms can be used to solve a search problem, such as: • Breadth First Search (BFS) • Depth First Search (DFS) • Greedy Best First Search (GBFS) • A* Search
- 6. Breadth First Search(BFS) The Breadth First Search (BFS) algorithm is used to search a graph data structure for a node that meets a set of criteria. It starts at the root of the graph and visits all nodes at the current depth level before moving on to the nodes at the next depth level. In short, BFS will visit all current depth level nodes before proceeding to the nodes at the next level of depth.
- 7. Pseudocode of thealgorithm: 1. Input graph, start node, and goal node 2. Define solution as a list 3. Define frontier as a queue 4. Define visited as a list 5. Append start node to frontier and visited 6. While the frontier is not empty: 7. Dequeue the frontier and store the value in the selected node 8. If the selected node is equal to the goal node, append the selected node to the solution, break from the loop, and return the solution. 9. If not, just append the selected node to the solution. 10.Loop through all neighbors of the selected node from the graph, append each neighbor to the frontier and visited if the neighbor is not yet in the visited list.
- 8. Solve Maze Problemwith BFS What is the solution and cost of the above Maze problem if we want to move from A to N?
- 9.
- 10. Below is thestep-to-step visualization of solving the search problem using the BFS algorithm: Append A to the Frontier.
- 11. Append A tothe Visited and BFS, then append A’s neighbor (B) to the Frontier. Finally, pop A from the Frontier.
- 12. Append B tothe Visited and BFS, then append B’s neighbor (C) to the Frontier. Finally, pop B from the Frontier.
- 13. Append C tothe Visited and BFS, then append C’s neighbor (D, G) to the Frontier. Finally, pop C from the Frontier.
- 14. Append D tothe Visited and BFS, then append D’s neighbor (E) to the Frontier. Finally, pop D from the Frontier.
- 15. Append G tothe Visited and BFS, then append G’s neighbor (H) to the Frontier. Finally, pop G from the Frontier.
- 16. Append E tothe Visited and BFS, then append E’s neighbor (F) to the Frontier. Finally, pop E from the Frontier.
- 17. Append H tothe Visited and BFS, then append H’s neighbor (K, I) to the Frontier. Finally, pop H from the Frontier.
- 18. Append F tothe Visited and BFS. Finally, pop F from the Frontier.
- 19. Append K tothe Visited and BFS, then append K’s neighbor (L) to the Frontier. Finally, pop K from the Frontier.
- 20. Append I tothe Visited and BFS, then append I’s neighbor (J) to the Frontier. Finally, pop I from the Frontier.
- 21. Append L tothe Visited and BFS, then append L’s neighbor (M) to the Frontier. Finally, pop L from the Frontier.
- 22. Append J tothe Visited and BFS. Finally, pop J from the Frontier.
- 23. Append M tothe Visited and BFS, then append M’s neighbor (N) to the Frontier. Finally, pop M from the Frontier.
- 24. Append N tothe Visited and BFS. Finally, pop N from the Frontier.
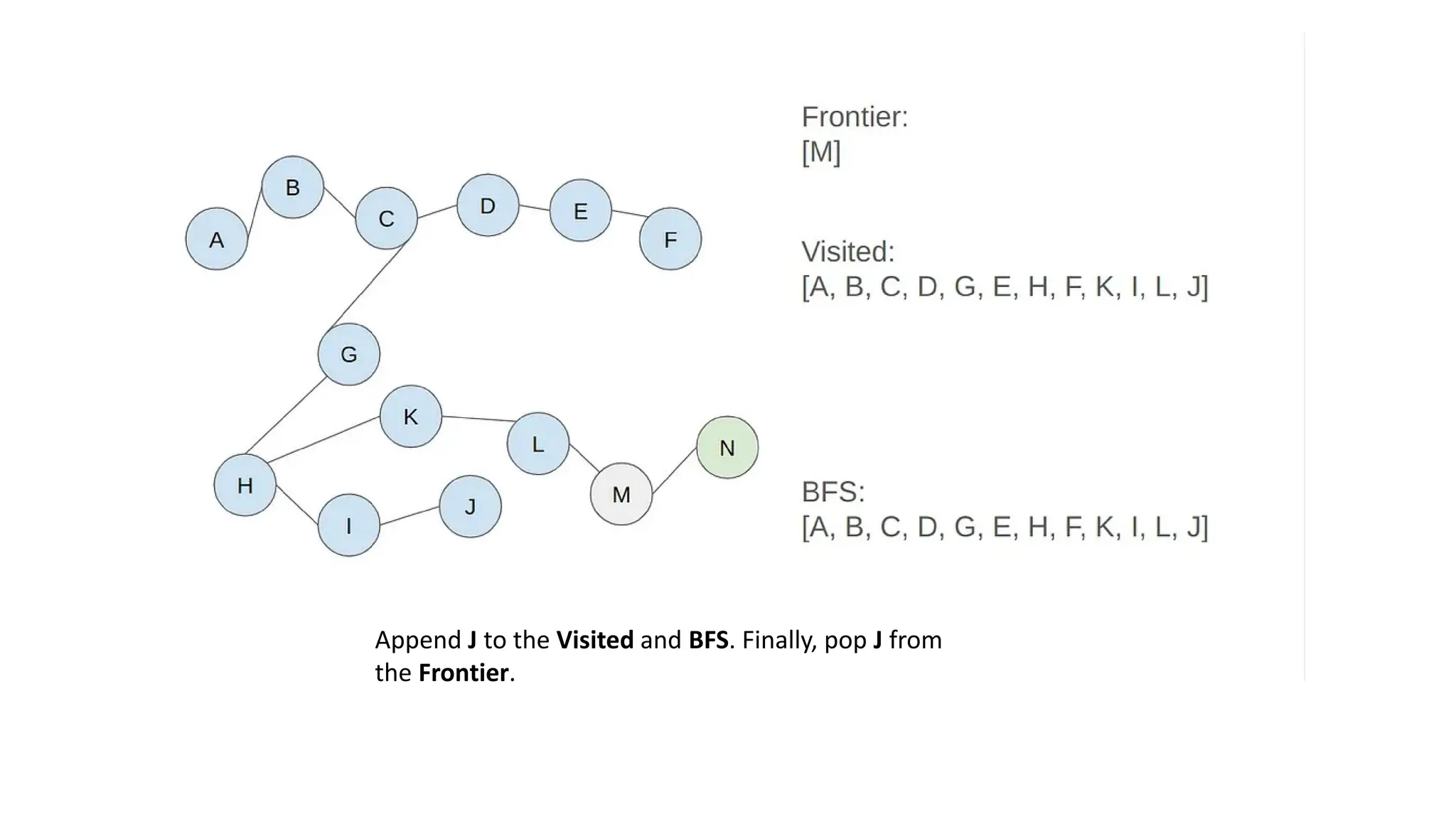
- 25. The answer tothe above question will be: • Solution: [A, B, C, D, G, E, H, F, K, I, L, J, M, N] • Costs: 13 (there are 13 nodes to step to reach the end node from the start node)
- 26.