Bsc cs ii dfs u-1 introduction to data structure

Course: BSC CS
Subject: Data Structure
Unit-1
Introduction to Data Structure

Data Structure
 A Data Structure is an aggregation of atomic and
composite data into a set with defined relationships.
 Structure means a set of rules that holds the data together.
 Taking a combination of data and fit them into such a
structure that we can define its relating rules, we create a
data structure.

Data structure
 A data structure in computer science is a way of
storing data in a computer so that it can be used
efficiently.
– An organization of mathematical and logical
concepts of data
– Implementation using a programming language
– A proper data structure can make the algorithm or
solution more efficient in terms of time and space

Data Structures: Properties
 Most of the modern programming languages support
a number of data structures.
 In addition, modern programming languages allow
programmers to create new data structures for an
application.
 Data structures can be nested.
 A data structure may contain other data structures
(array of arrays, array of records, record of records,
record of arrays, etc.)

What is Data Structures?
 A data structure is defined by
 (1) the logical arrangement of data elements,
combined with
 (2) the set of operations we need to access the
elements.

What is Data Structures?
 Example:
 library is composed of elements (books)
 Accessing a particular book requires knowledge
of the arrangement of the books
 Users access books only through the librarian

Cont..
 An algorithm is a finite set of instructions that, if
followed, accomplishes a particular task.
 All the algorithms must satisfy the following criteria:
– Input
– Output
– Precision (Definiteness)
– Effectiveness
– Finiteness

TYPES OF DATA STRUCURE
 Primitive & Non Primitive Data Structures
 Primitive data Structure
 The integers, reals, logical data, character data,
pointer and reference are primitive data structures.
 Data structures that normally are directly operated
upon by machine-level instructions are known as
primitive data structures.

Non-primitive Data Structures
 These are more complex data structures. These data
structures are derived from the primitive data
structures.
 They stress on formation of sets of homogeneous and
heterogeneous data elements.
 The different operations that are to be carried out on
data are nothing but designing of data structures.
 CREATE
 DESTROY
 SELECT
 UPDATE

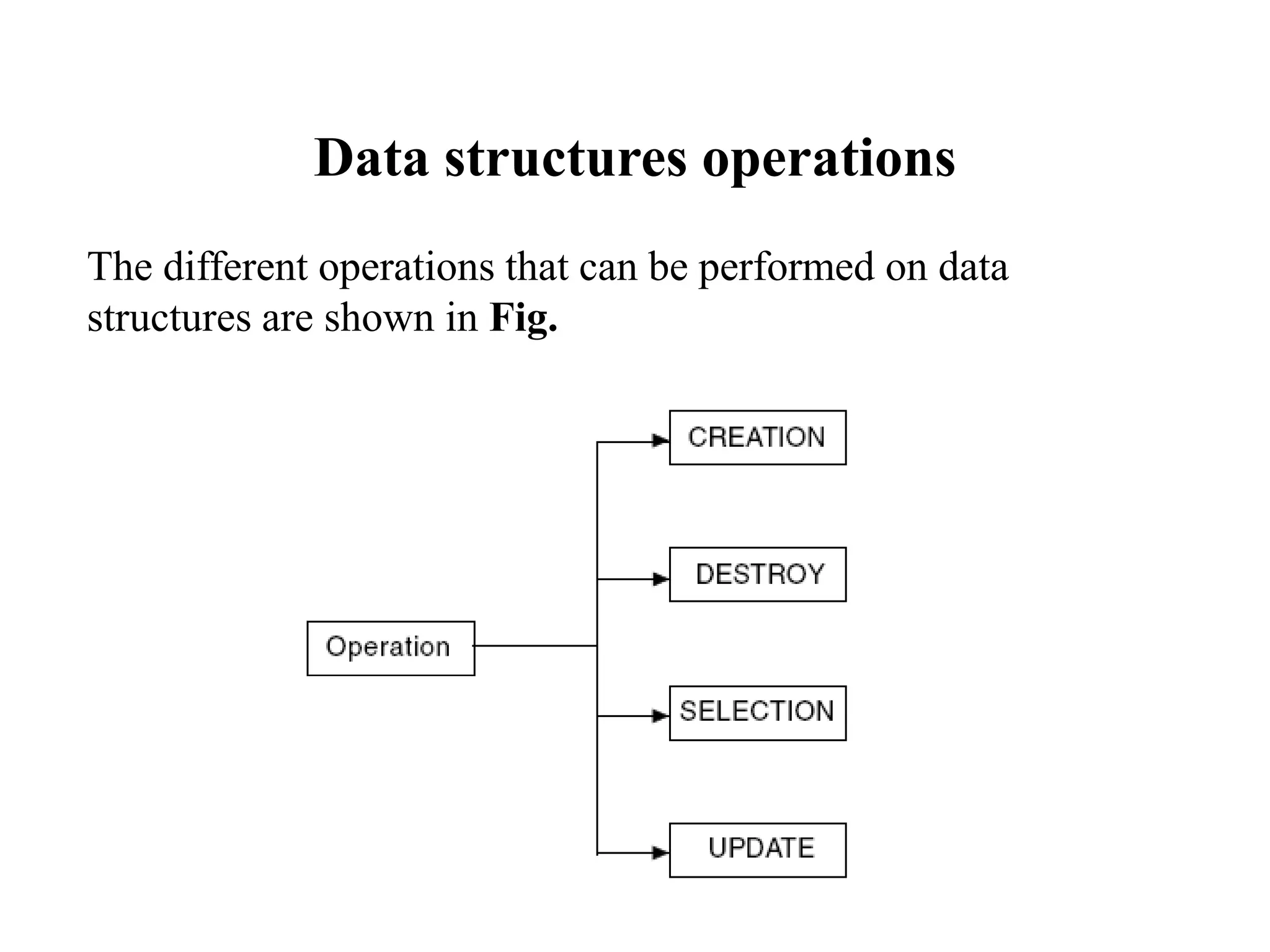
Data structures operations
The different operations that can be performed on data
structures are shown in Fig.

Performance Analysis
 There are problems and algorithms to solve them.
 Problems and problem instances.
 Example: Sorting data in ascending order.
 Problem: Sorting
 Problem Instance: e.g. sorting data (2 3 9 5 6 8)
 Algorithms: Bubble sort, Merge sort, Quick sort,
Selection sort, etc.
 Which is the best algorithm for the problem? How do
we judge?

Performance Analysis
 Two criteria are used to judge algorithms:
(i) time complexity (ii) space complexity.
 Space Complexity of an algorithm is the amount of
memory it needs to run to completion.
 Time Complexity of an algorithm is the amount of
CPU time it needs to run to completion.

Space Complexity: Example 1
1. Algorithm abc (a, b, c)
2. {
3. return a+b+b*c+(a+b-c)/(a+b)+4.0;
4. }
For every instance 3 computer words required to
store variables: a, b, and c.
Therefore Sp()= 3. S(P) = 3.

Time Complexity
 What is a program step?
 a+b+b*c+(a+b)/(a-b)  one step;
 comments  zero steps;
 while (<expr>) do  step count equal to the
number of times <expr> is executed.
 for i=<expr> to <expr1> do  step count equal to
number of times <expr1> is checked.

Performance Measurement
 Which is better?
 T(P1) = (n+1) or T(P2) = (n2 + 5).
 T(P1) = log (n2 + 1)/n! or T(P2) = nn(nlogn)/n2.
 Complex step count functions are difficult to compare.
 For comparing, ‘rate of growth’ of time and space
complexity functions is easy and sufficient.

Big O Notation
 Big O of a function gives us ‘rate of growth’ of the
step count function f(n), in terms of a simple function
g(n), which is easy to compare.
 Definition:
[Big O] The function f(n) = O(g(n)) (big ‘oh’ of g of
n) if
there exist positive constants c and n0 such that f(n) <=
c*g(n) for all n, n>=n0. See graph on next slide.
 Example: f(n) = 3n+2 is O(n) because 3n+2 <= 4n for
all n >= 2. c = 4, n0 = 2. Here g(n) = n.

Big O Notation
 Example: f(n) = 10n2+4n+2 is O(n2)
because 10n2+4n+2 <= 11n2 for all n >=5.
 Example: f(n) = 6*2n+n2 is O(2n)
because 6*2n+n2 <=7*2n for all n>=4.
 Algorithms can be:
 O(1)  constant; O(log n)  logrithmic; O(nlogn);
O(n) linear; O(n2)  quadratic; O(n3)  cubic; O(2n)
 exponential.

Big O Notation
 Now it is easy to compare time or space complexities
of algorithms.
 Which algorithm complexity is better?
 T(P1) = O(n) or T(P2) = O(n2)
 T(P1) = O(1) or T(P2) = O(log n)
 T(P1) = O(2n) or T(P2) = O(n10)

Linear & Non Linear Data Structures
 Linear data structures:- in which insertion and deletion
is possible in linear fashion .
 example:- arrays, linked lists.
 Non linear data structures:-in which it is not possible.
example:- trees ,stacks

LINEAR DATA STRUCTURE Array
 Array is linear, homogeneous data structures whose
elements are stored in contiguous memory locations.

Arrays
 Array: a set of pairs, <index, value>
 Data structure
 For each index, there is a value associated with
that index.
 Representation (possible)
 Implemented by using consecutive memory.
 In mathematical terms, we call this a
correspondence or a mapping.

Initializing Arrays
 Using a loop:
 for (int i = 0; i < myList.length; i++)
 myList[i] = i;
 Declaring, creating, initializing in one step:
 double[] myList = {1.9, 2.9, 3.4, 3.5};
 This shorthand syntax must be in one statement.

Declaring and Creating in One Step
 datatype[] arrayname = new
 datatype[arraySize];
 double[] myList = new double[10];
 datatype arrayname[] = new
datatype[arraySize];
 double myList[] = new double[10];

Sparse Matrix[2]
 A sparse matrix is a matrix that has many zero entries.






















0002800
0000091
000000
006000
0003110
150220015
• This is a __×__ matrix.
• There are _____ entries.
• There are _____ nonzero entries.
• There are _____ zero entries.
Consider we use a 2D array to represent a n×n sparse matrix. How many entries
are required? _____ entries. The space complexity is O( ).

Sparse Matrix
 If n is large, say n = 5000, we need 25 million elements to store
the matrix.
 25 million units of time for operation such as addition and
transposition.
 Using a representation that stores only the nonzero entries can
reduce the space and time requirements considerably.

Sparse Matrix Representation
 The information we need to know
 The number of rows
 The number of columns
 The number of nonzero entries
 All the nonzero entries are stored in an array. Therefore, we
also have to know
 The capacity of the array
 Each element contains a triple <row, col, value> to store.
 The triples are ordered by rows and within rows by
columns.

Sparse Matrix Representation
class SparseMatrix;
class MatrixEntry {
friend class SparseMatrix;
private:
int row, col, value;
};
class SparseMatrix {
private:
int rows, cols, terms, capacity;
MatrixEntry *smArray;
};

The array as an ADT
 When considering an ADT we are more concerned
with the operations that can be performed on an array.
 Aside from creating a new array, most languages
provide only two standard operations for arrays,
one that retrieves a value, and a second that stores
a value.
 The advantage of this ADT definition is that it
clearly points out the fact that the array is a more
general structure than “a consecutive set of
memory locations.”

Exercise : Bubble Sort
int[] myList = {2, 9, 5, 4, 8, 1, 6}; // Unsorted
Pass 1: 2, 5, 4, 8, 1, 6, 9
Pass 2: 2, 4, 5, 1, 6, 8, 9
Pass 3: 2, 4, 1, 5, 6, 8, 9
Pass 4: 2, 1, 4, 5, 6, 8, 9
Pass 5: 1, 2, 4, 5, 6, 8, 9
Pass 6: 1, 2, 4, 5, 6, 8, 9

Tower of Hanoi[3]
 The Objective is to transfer the entire tower to one of
the other pegs.
 However you can only move one disk at a time and
you can never stack a larger disk onto a smaller disk.
Try to solve it in fewest possible moves.

References
1) An introduction to Datastructure with application by jean Trembley and
sorrenson
2) Data structures by schaums and series –seymour lipschutz
3) http://en.wikipedia.org/wiki/Book:Data_structures
4) http://www.amazon.com/Data-Structures-Algorithms
5) http://www.amazon.in/Data-Structures-Algorithms-Made-
Easy/dp/0615459811/
6) http://www.amazon.in/Data-Structures-SIE-Seymour-Lipschutz/dp
List of Images
1. Data structures by schaums and series –seymour lipschutz
2. http://en.wikipedia.org/wiki/Book:Data_structures
3. http://en.wikipedia.org/wiki/tower of hanoi
4. http://en.wikipedia.org/wiki/tower of hanoi

Bsc cs ii dfs u-1 introduction to data structure

More Related Content

What's hot

Similar to Bsc cs ii dfs u-1 introduction to data structure

More from Rai University

Recently uploaded

Bsc cs ii dfs u-1 introduction to data structure