This document discusses various sorting algorithms and their complexities. It begins by defining an algorithm and complexity measures like time and space complexity. It then defines sorting and common sorting algorithms like bubble sort, selection sort, insertion sort, quicksort, and mergesort. For each algorithm, it provides a high-level overview of the approach and time complexity. It also covers sorting algorithm concepts like stable and unstable sorting. The document concludes by discussing future directions for sorting algorithms and their applications.








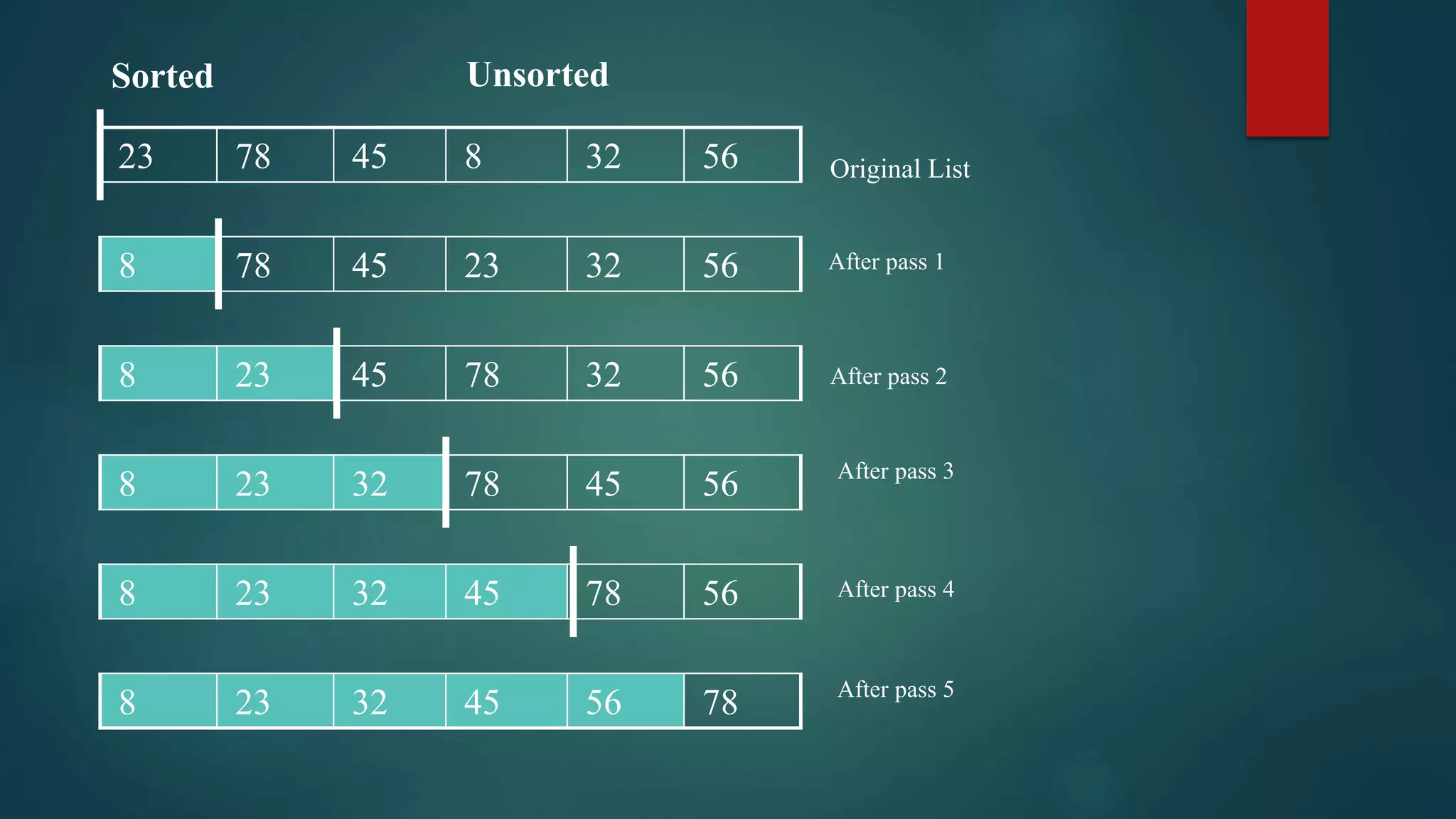
![Bubble Sort
• Simple and uncomplicated
• Largest element placer at last
• Compare neighboring elements
• Swap if out of order
• Two nested loops
• O(n2)
for (i=0; i<n-1; i++) {
for (j=0; j<n-1-i; j++)
if (a[j+1] < a[j]) { /* compare neighbors */
tmp = a[j]; /* swap a[j] and a[j+1] */
a[j] = a[j+1];
a[j+1] = tmp;
}](https://image.slidesharecdn.com/presentation-160616064245/75/Sorting-Algorithms-9-2048.jpg)

![Selection Sort Algorithm
public static void selectionSort(int[] list)
{ int min;
int temp;
for(int i = 0; i < list.length - 1; i++) {
min = i;
for(int j = i + 1; j < list.length; j++)
if( list[j] < list[min] )
min = j;
temp = list[i];
list[i] = list[min];
list[min] = temp;
}
}](https://image.slidesharecdn.com/presentation-160616064245/75/Sorting-Algorithms-12-2048.jpg)