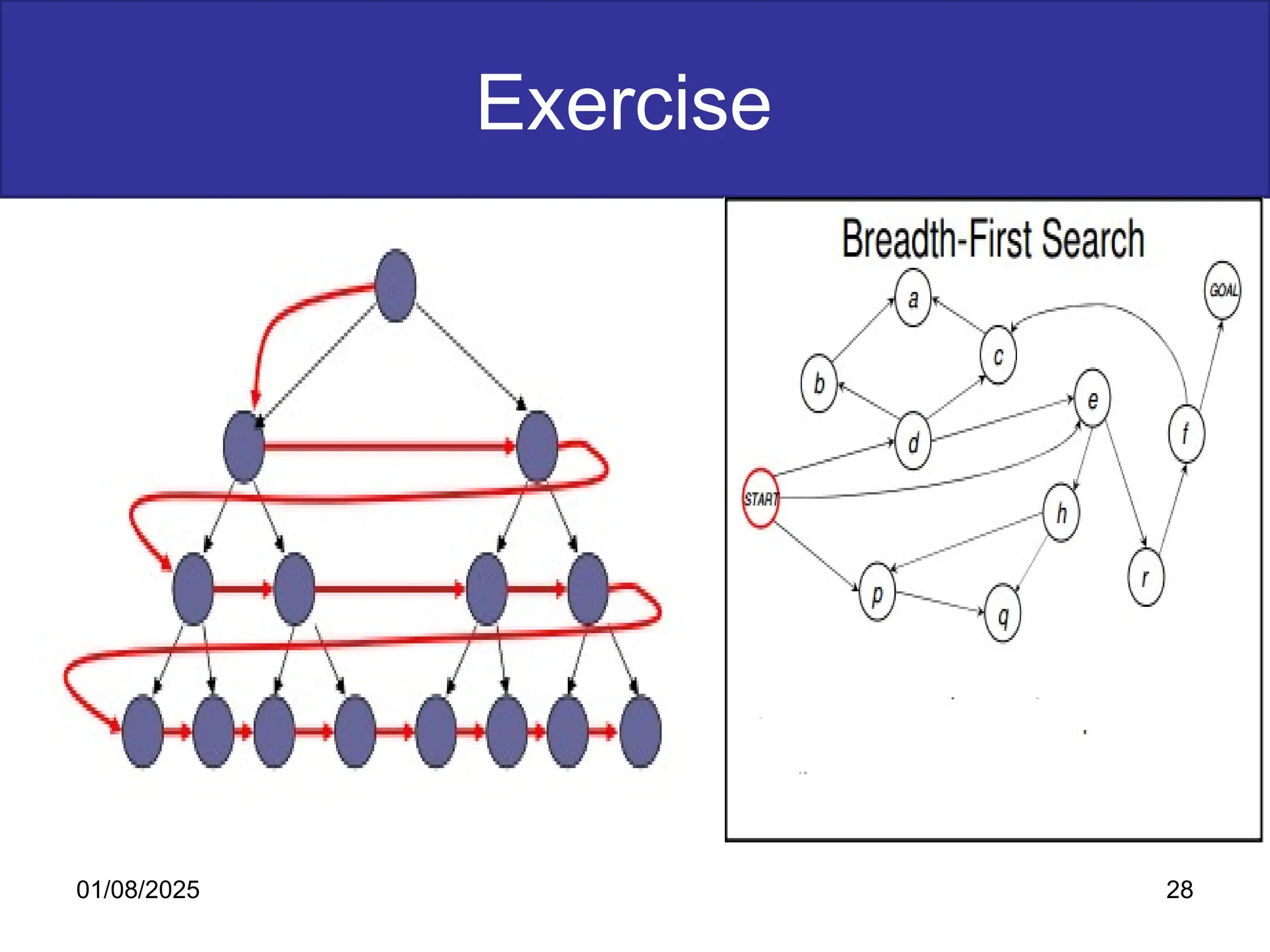
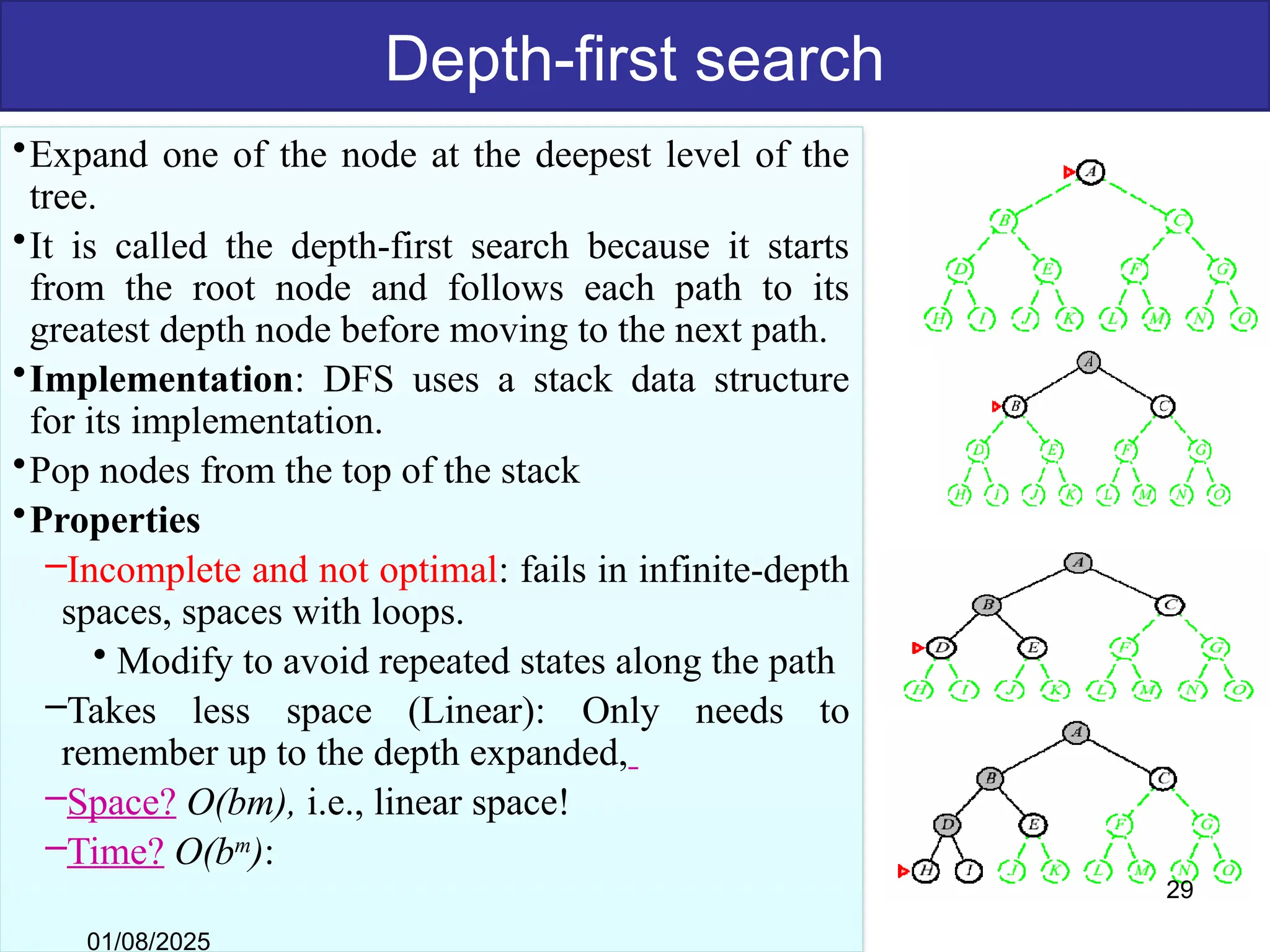
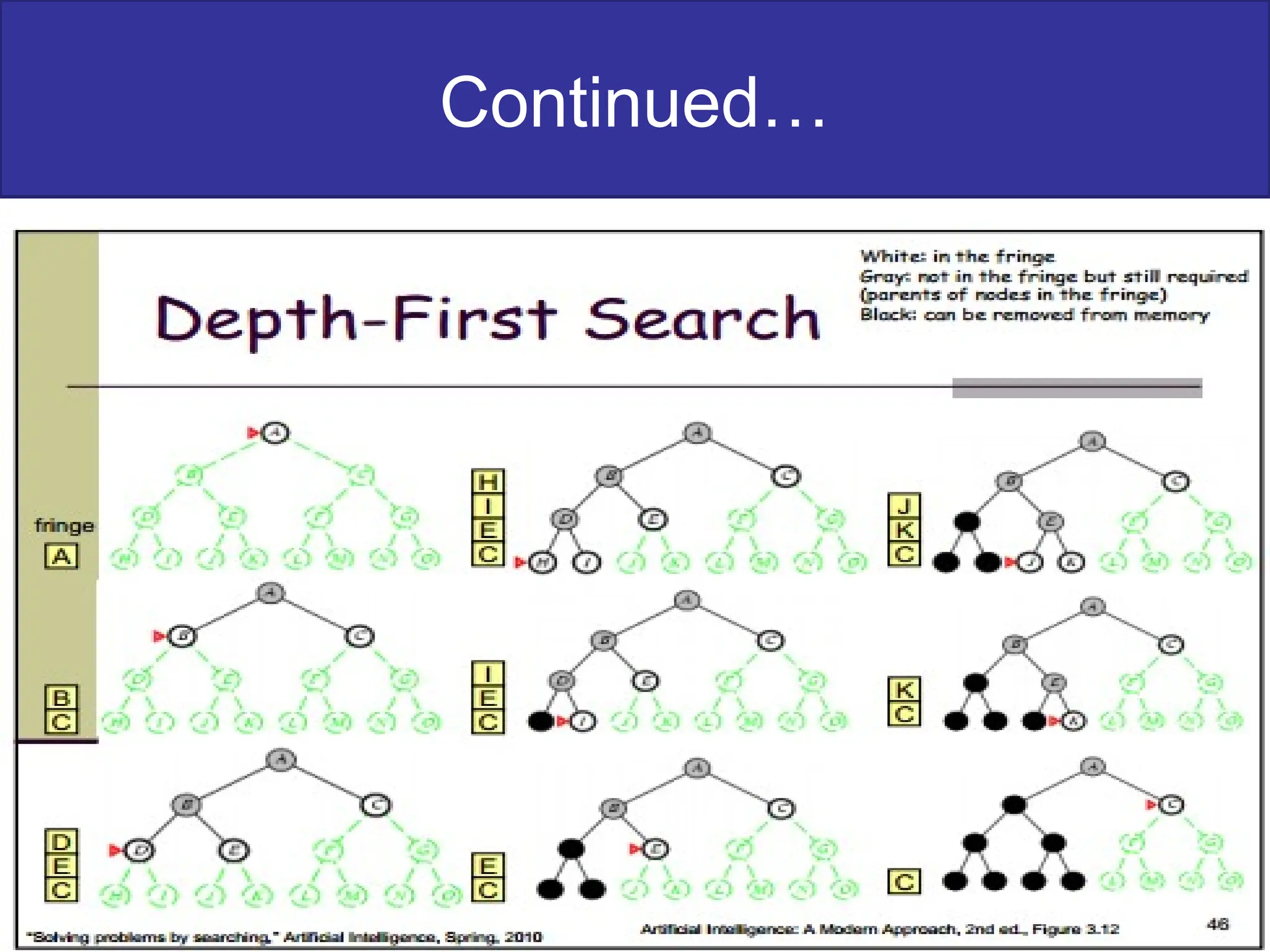
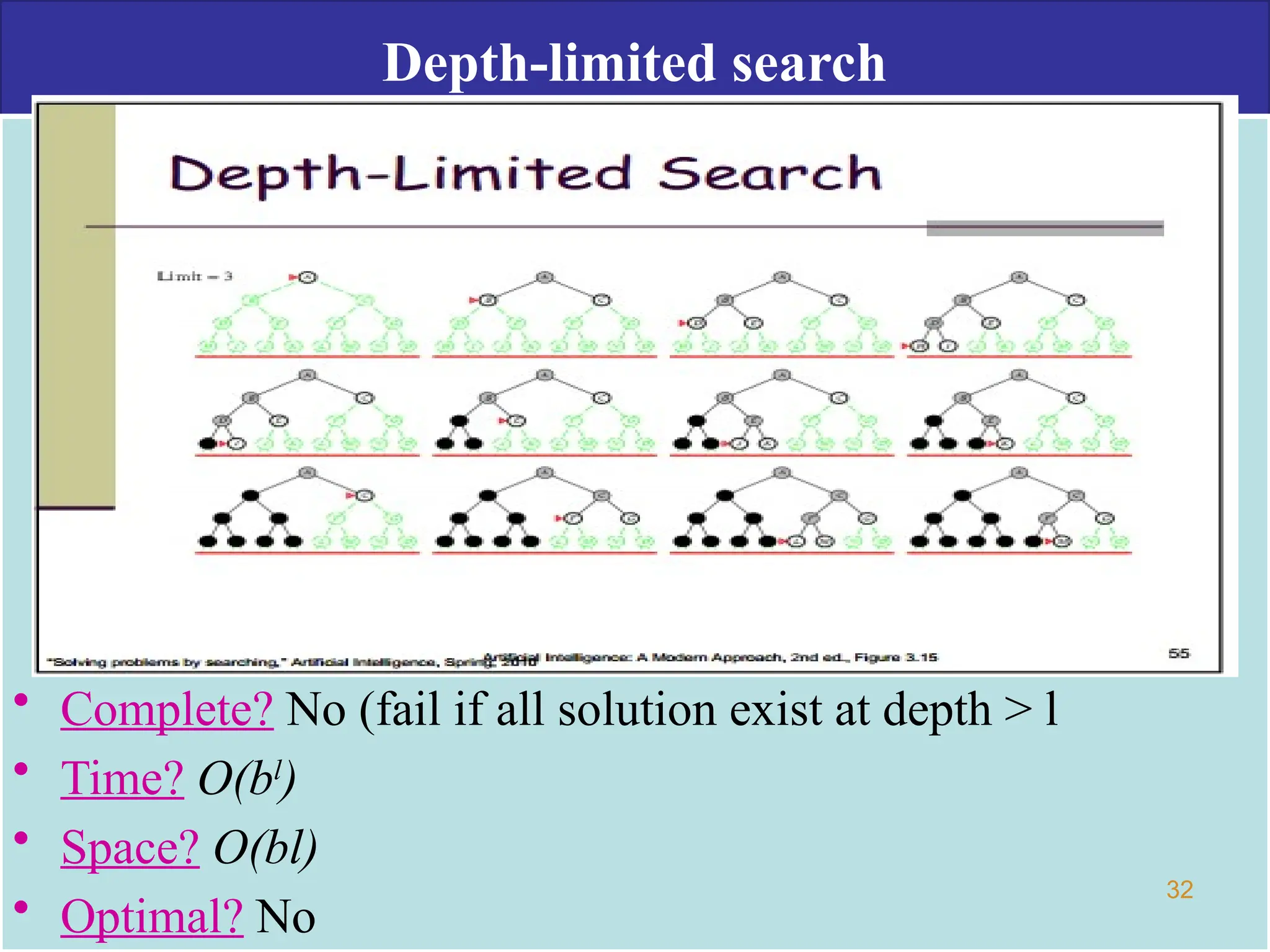
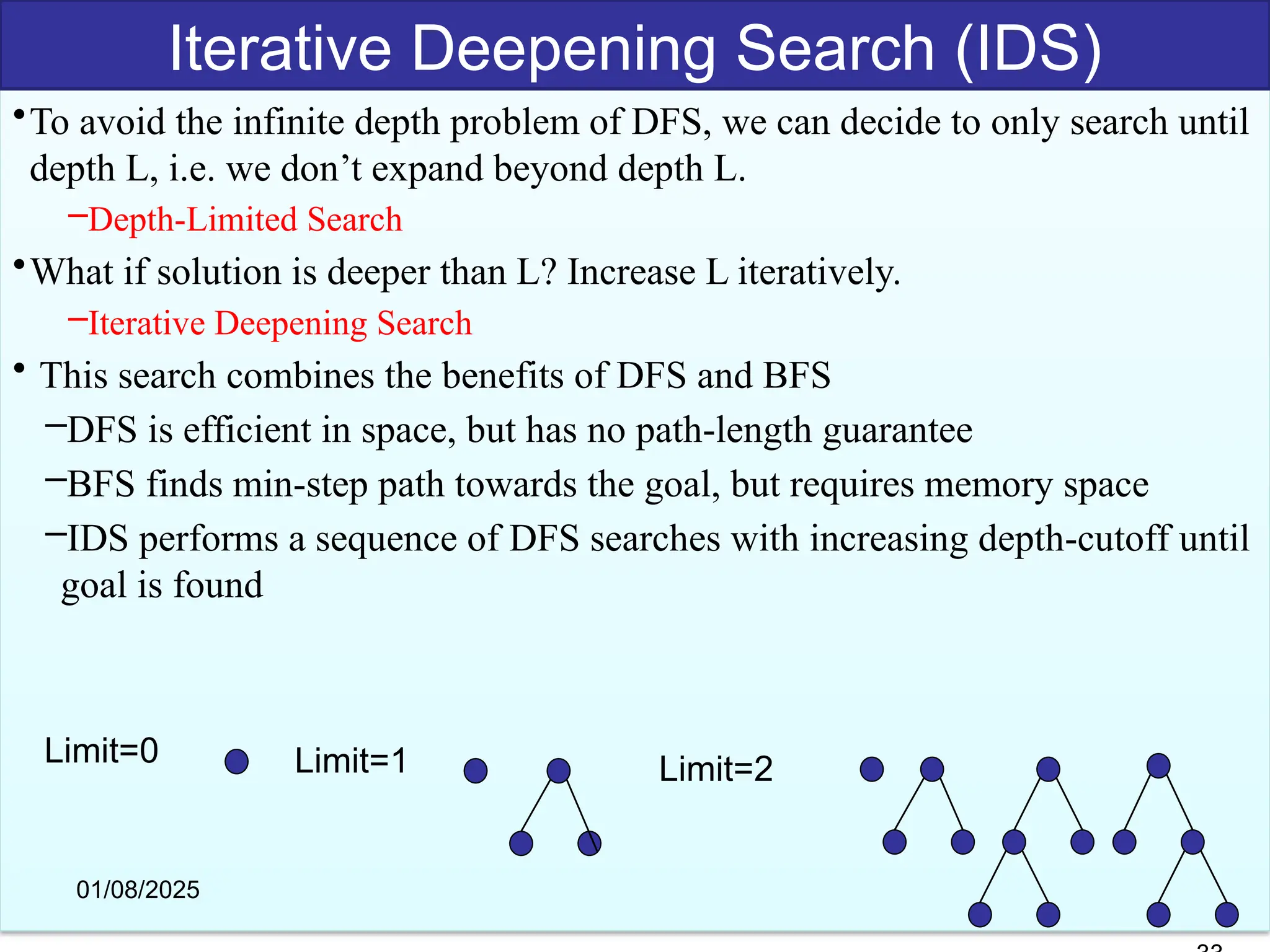
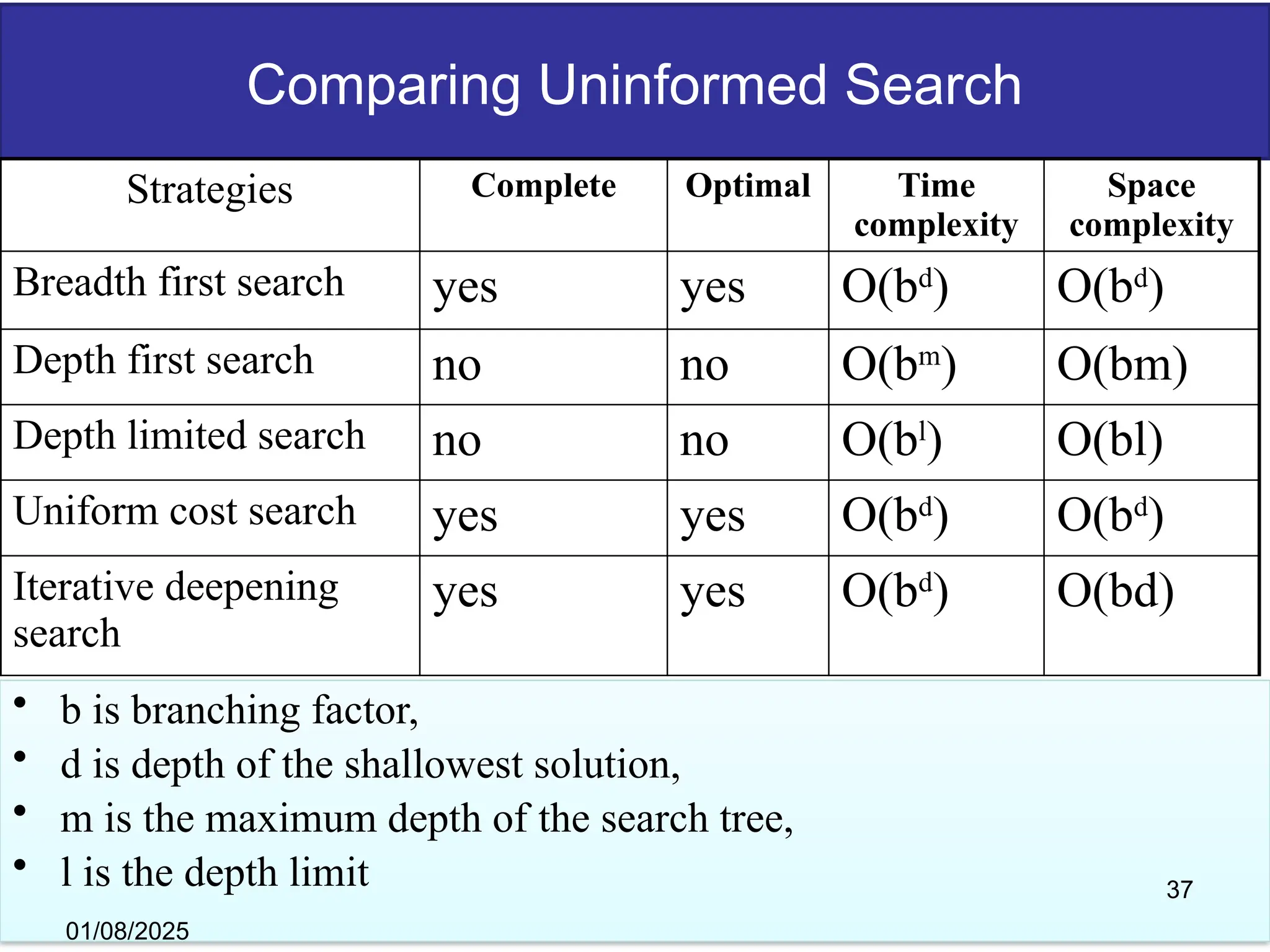
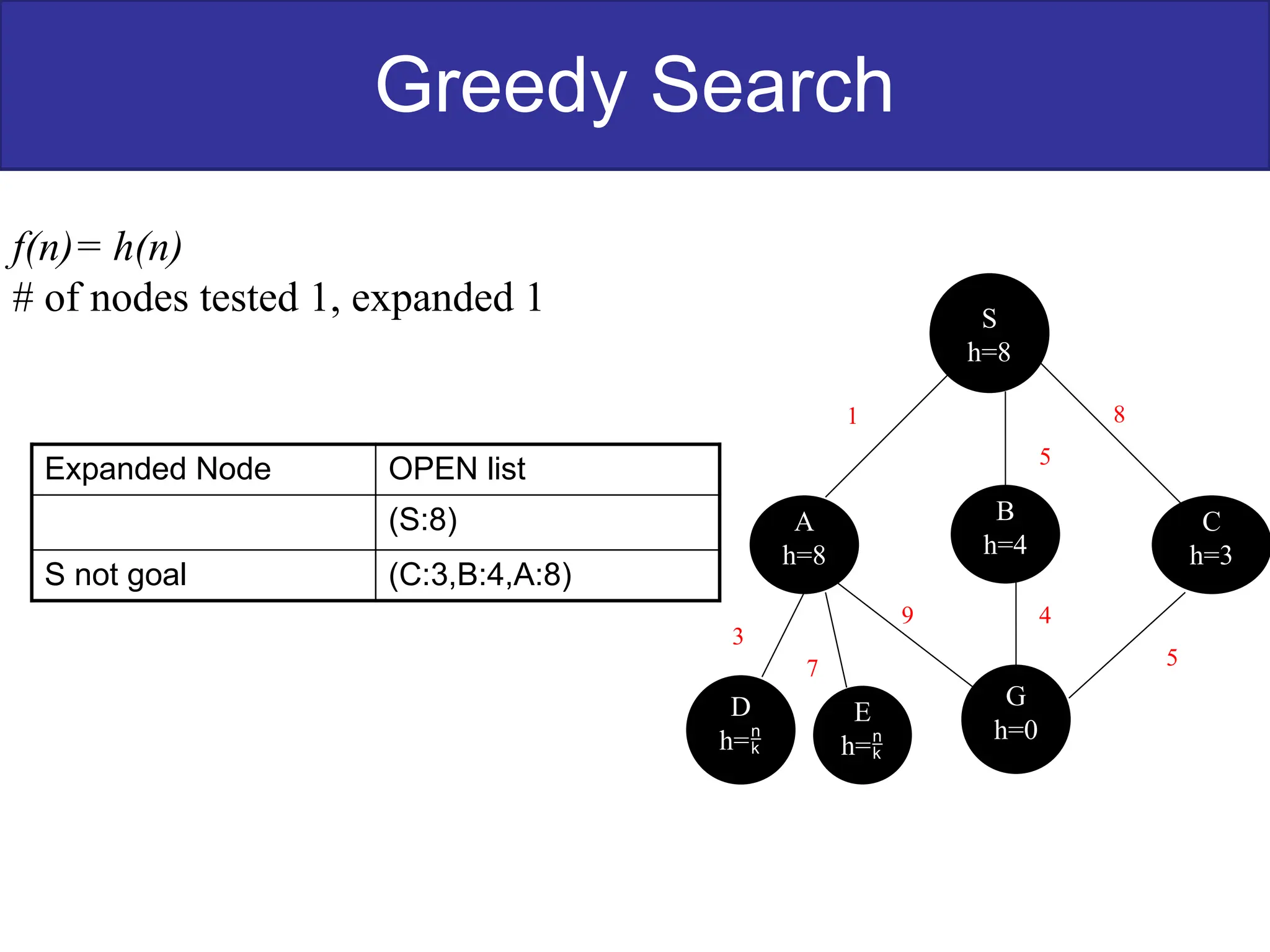
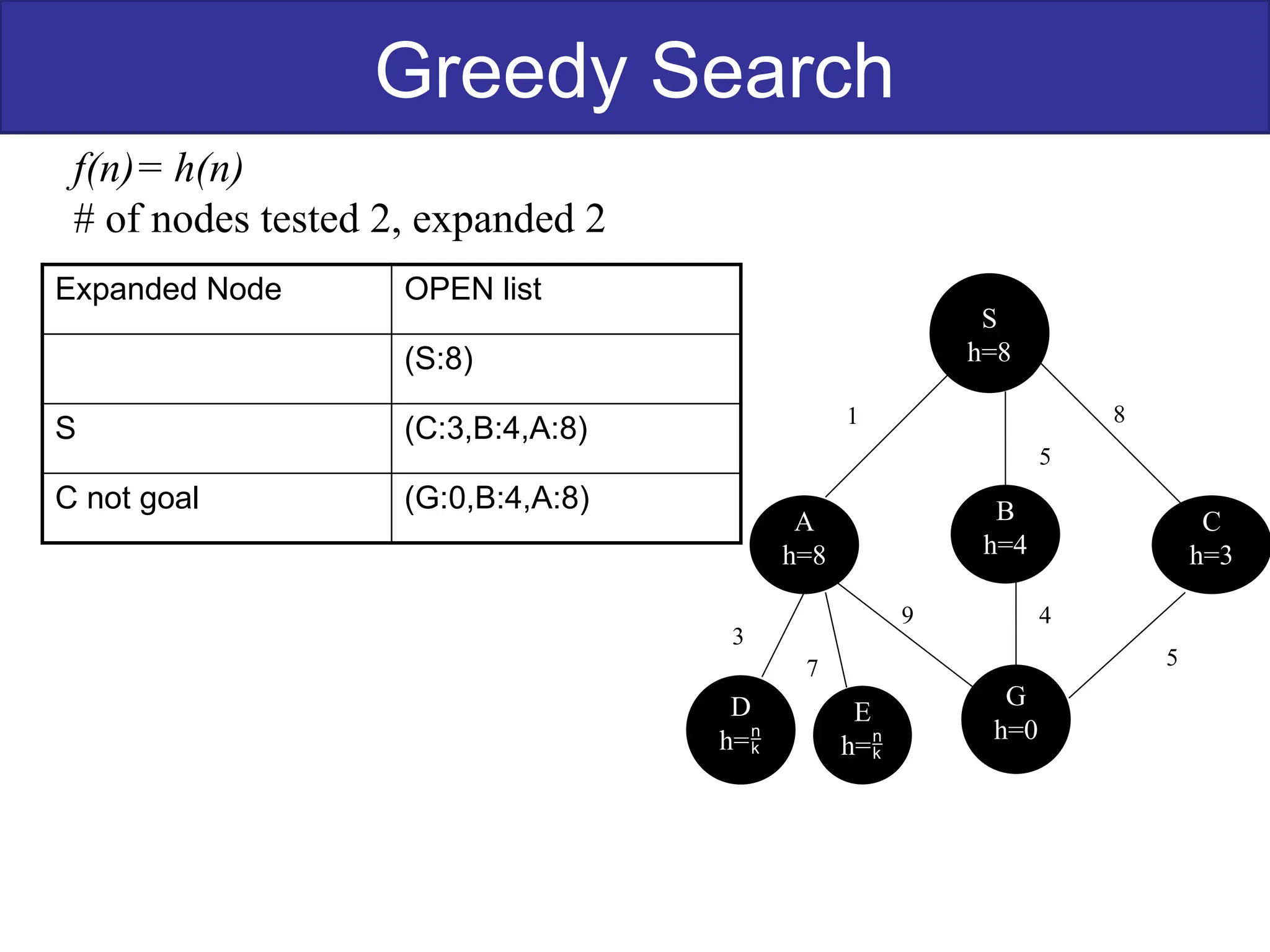
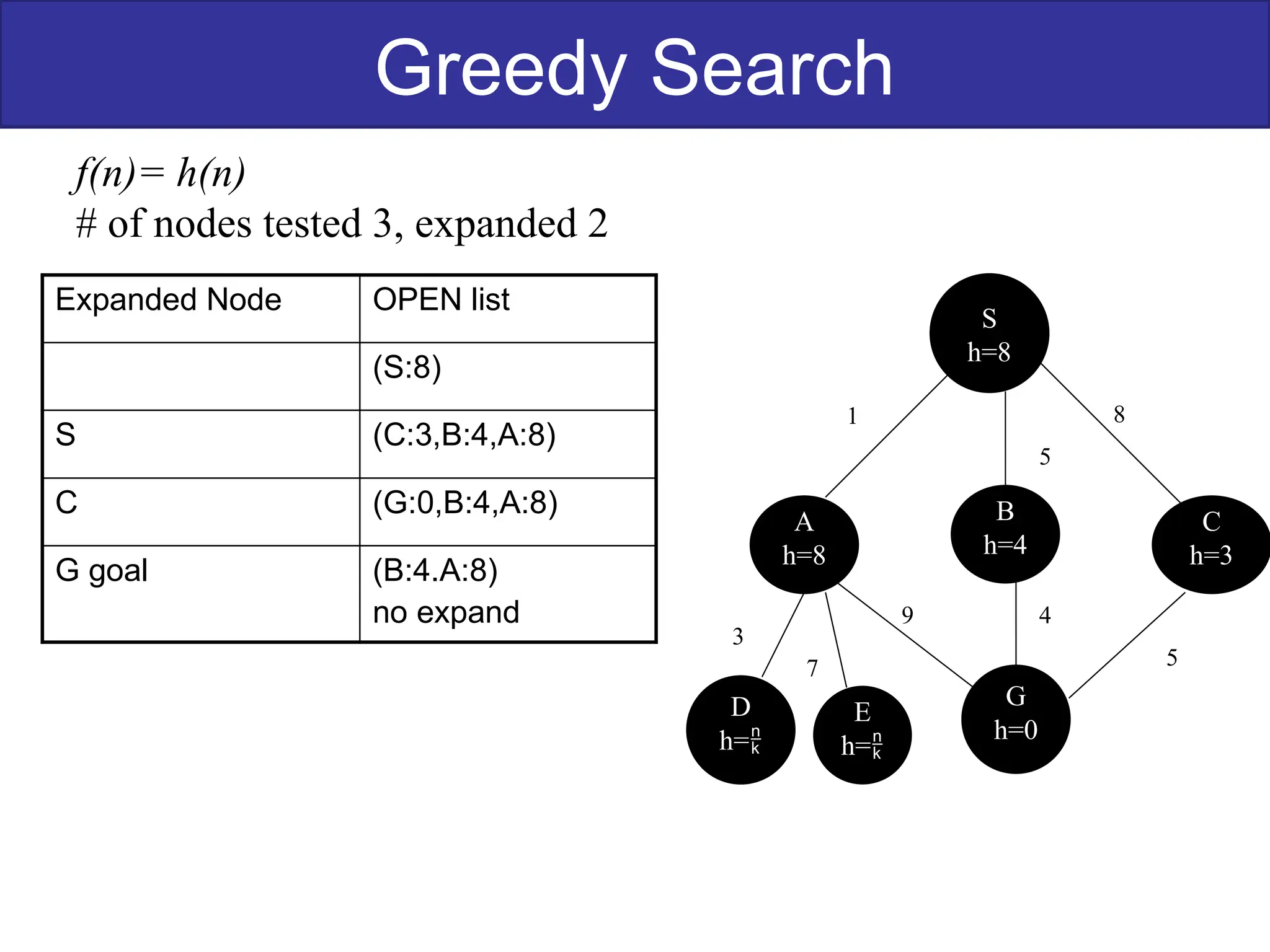
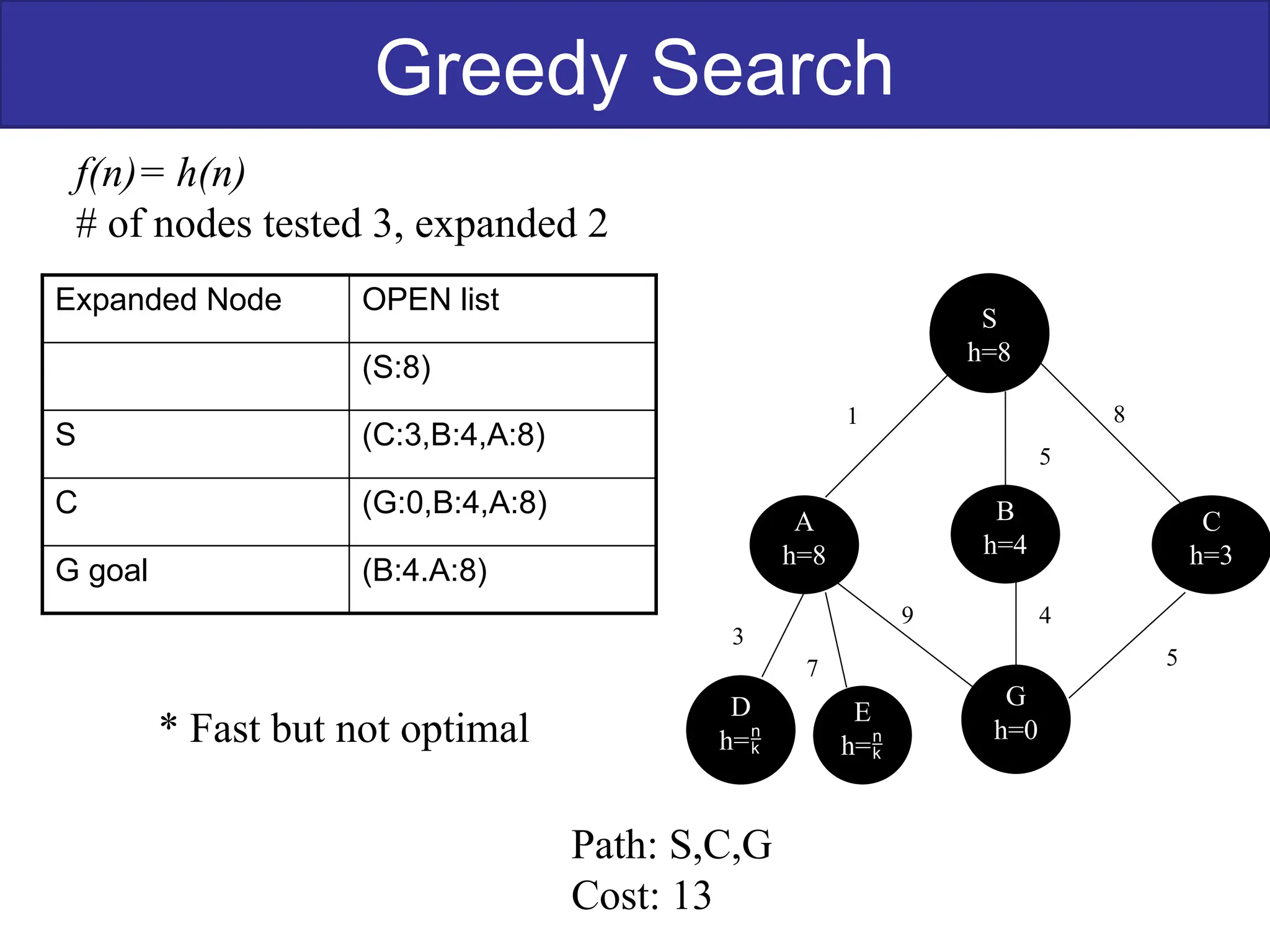
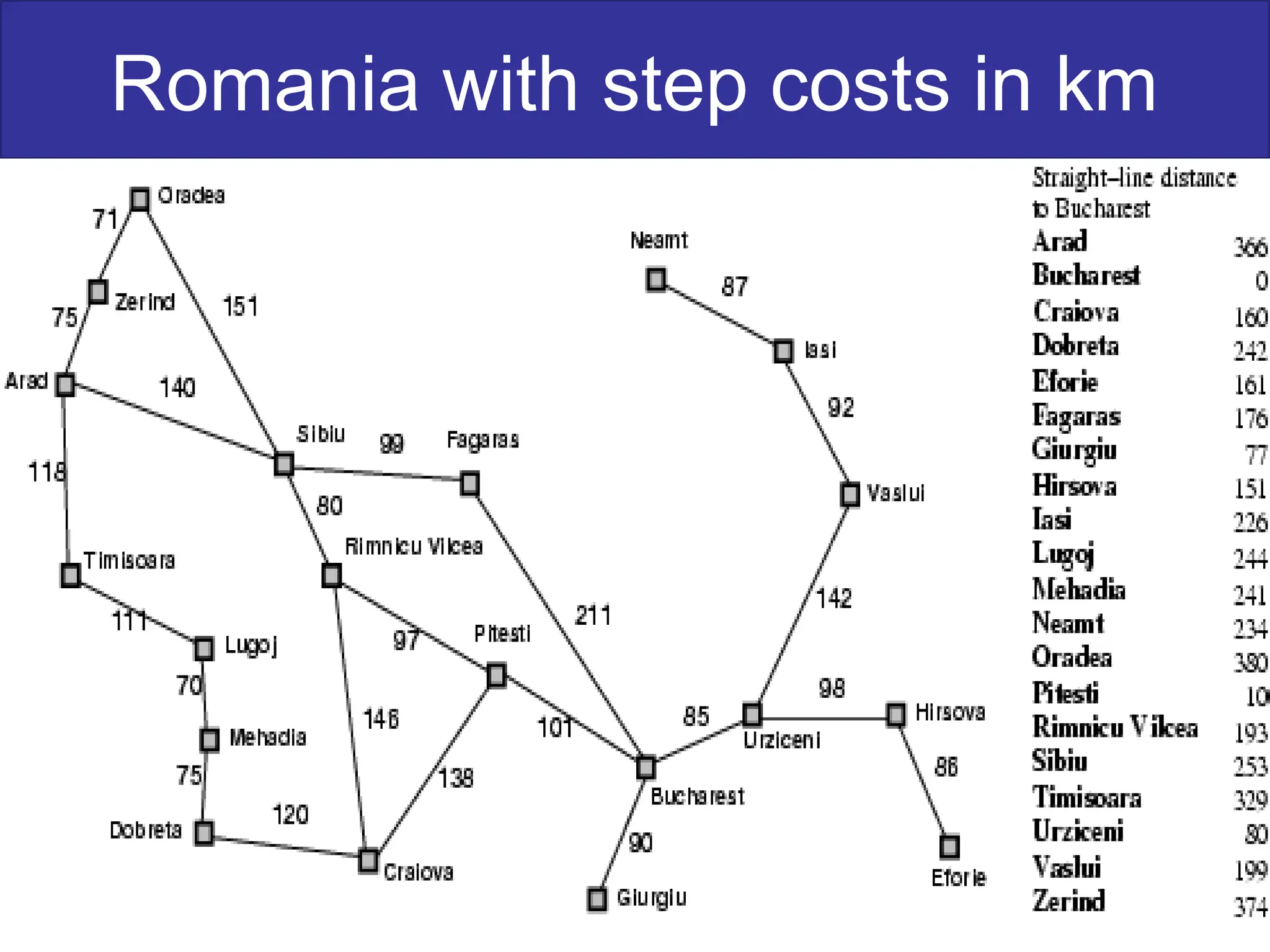
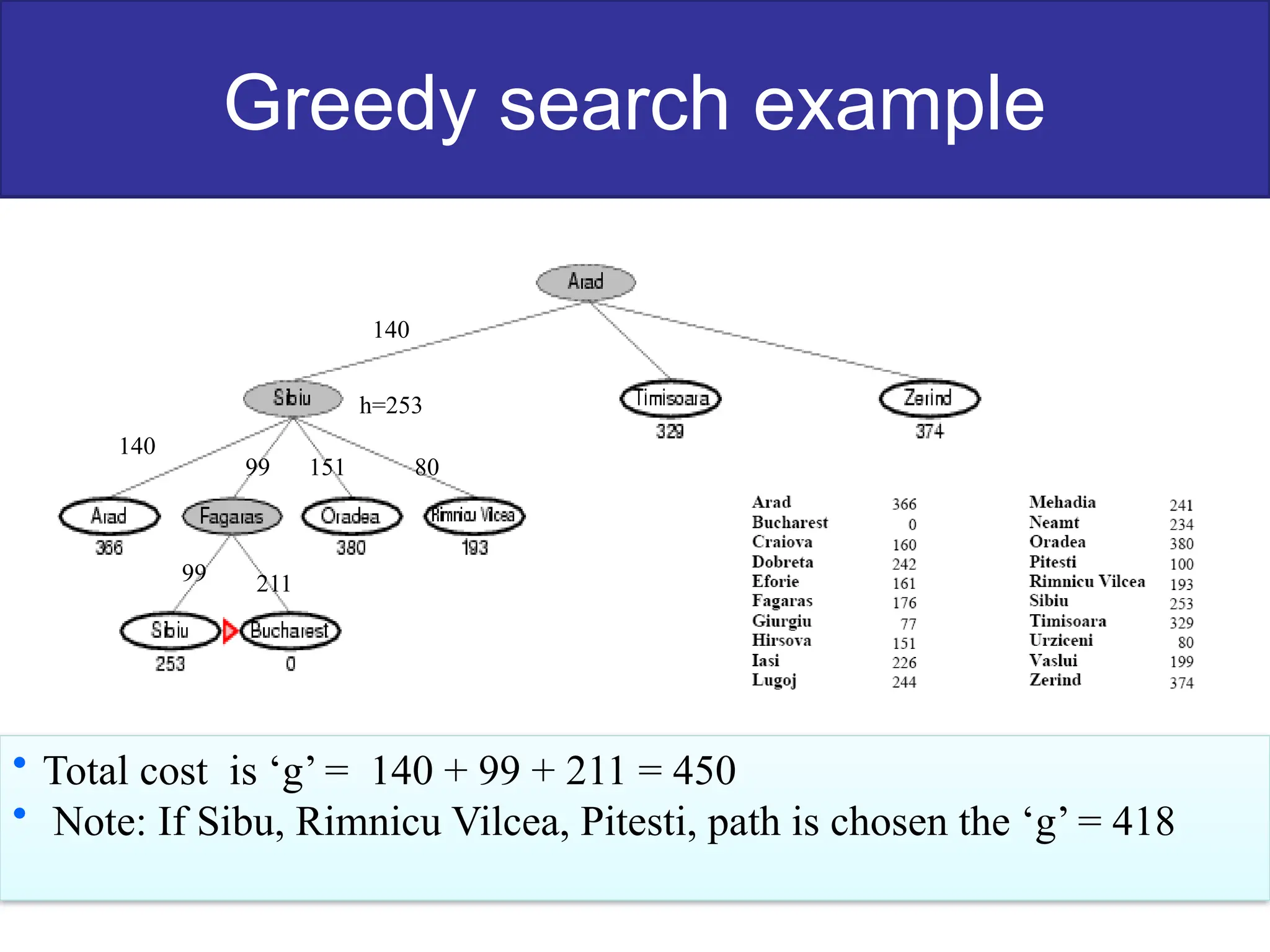
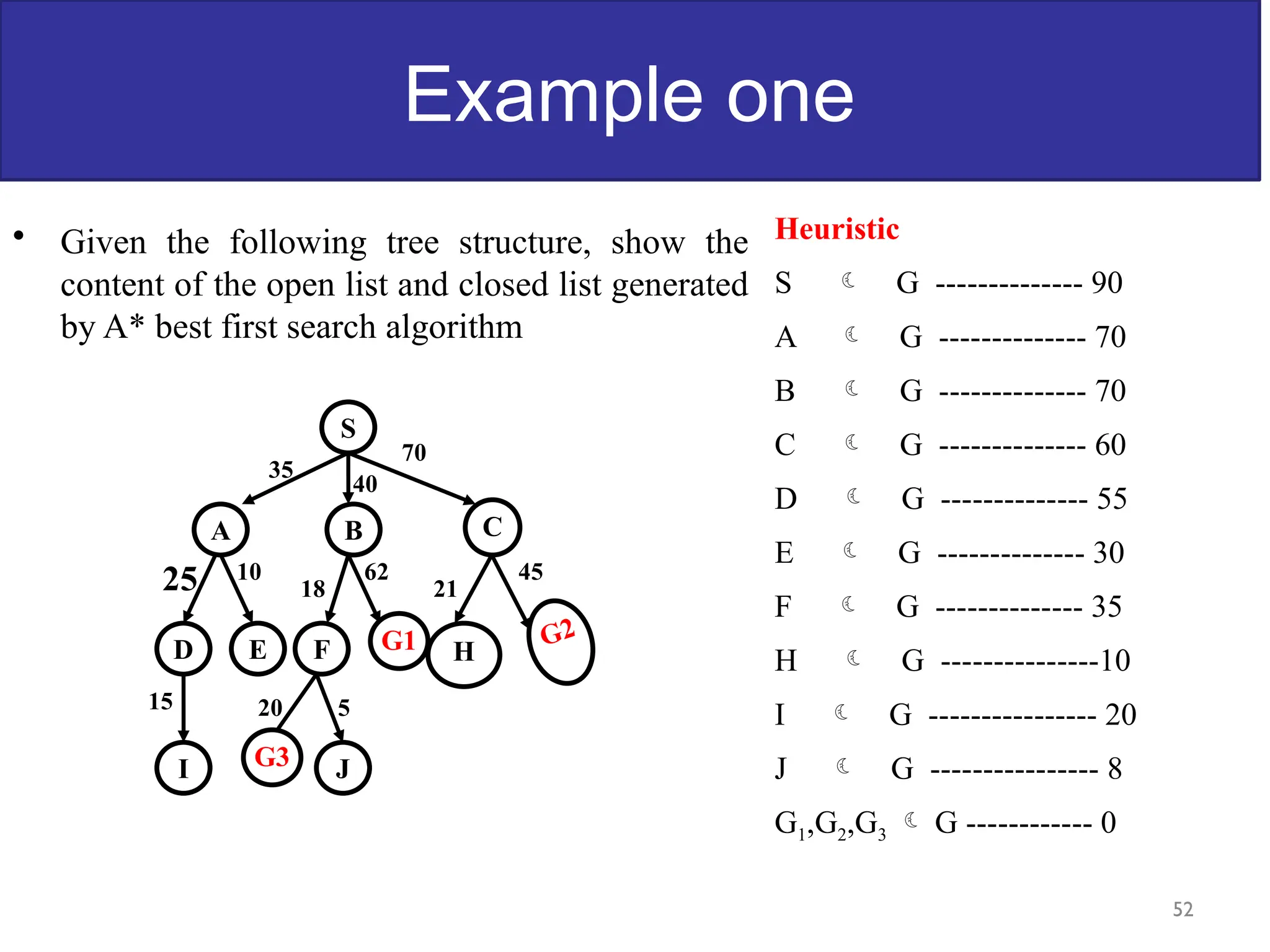
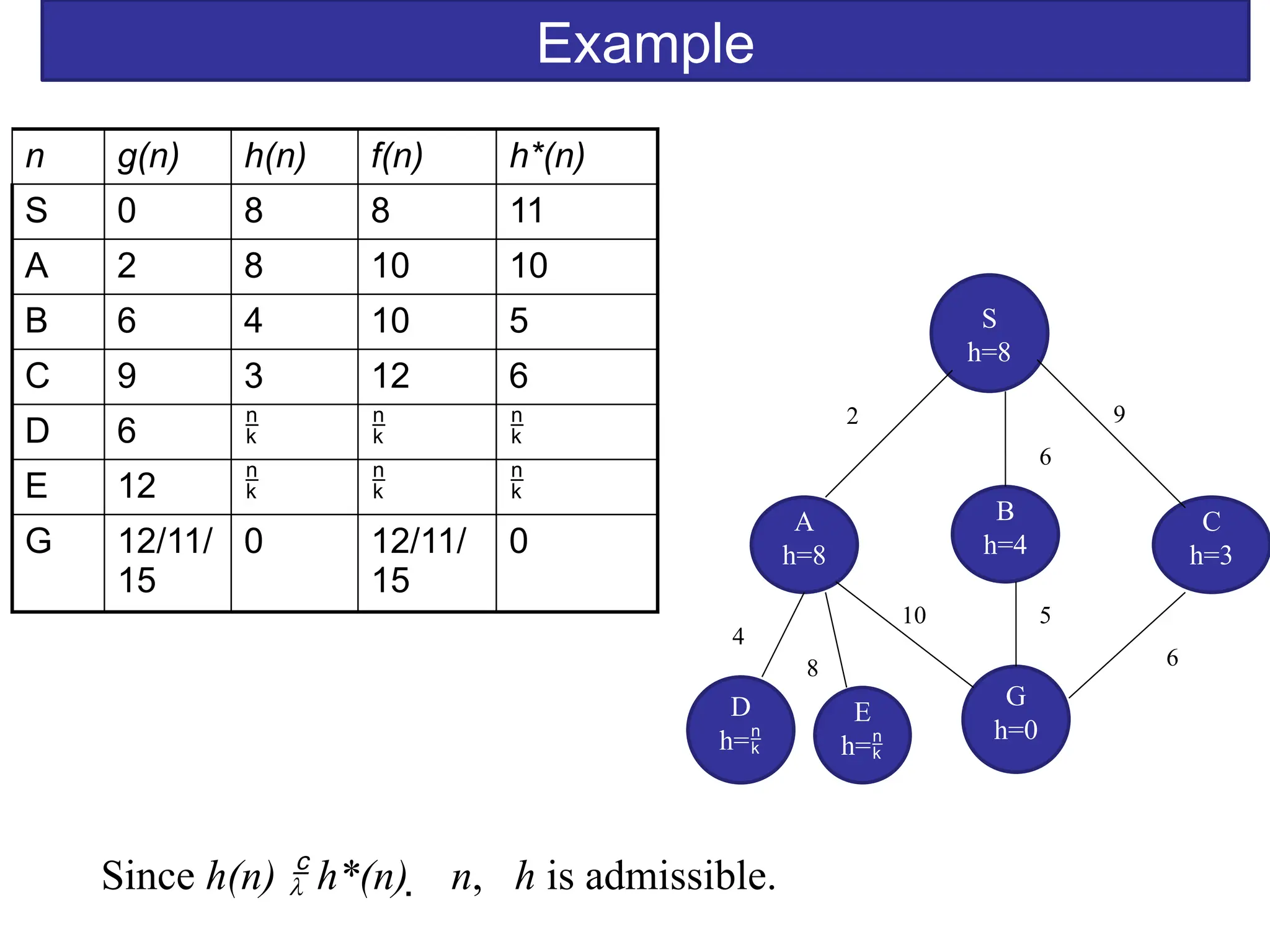
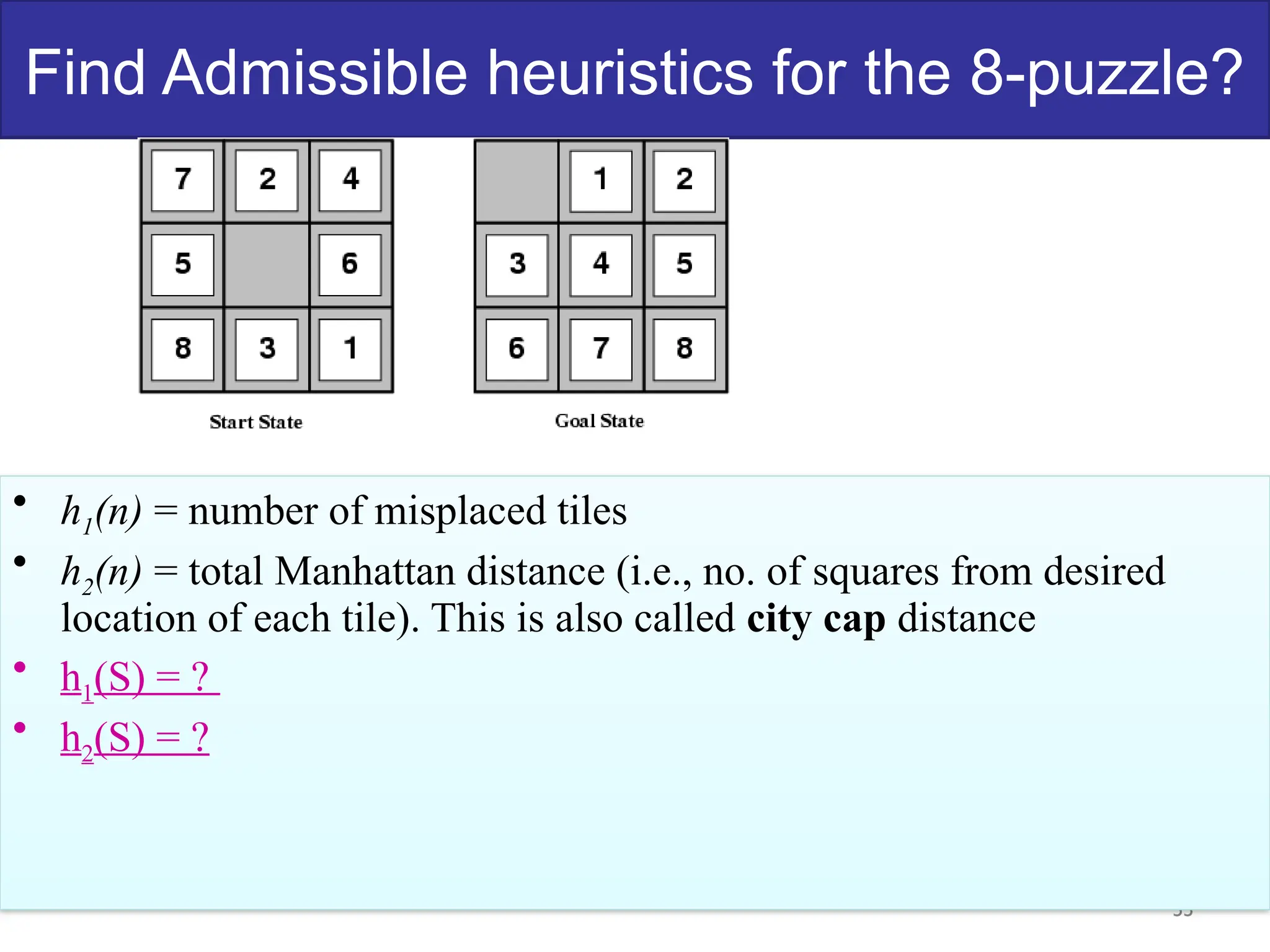
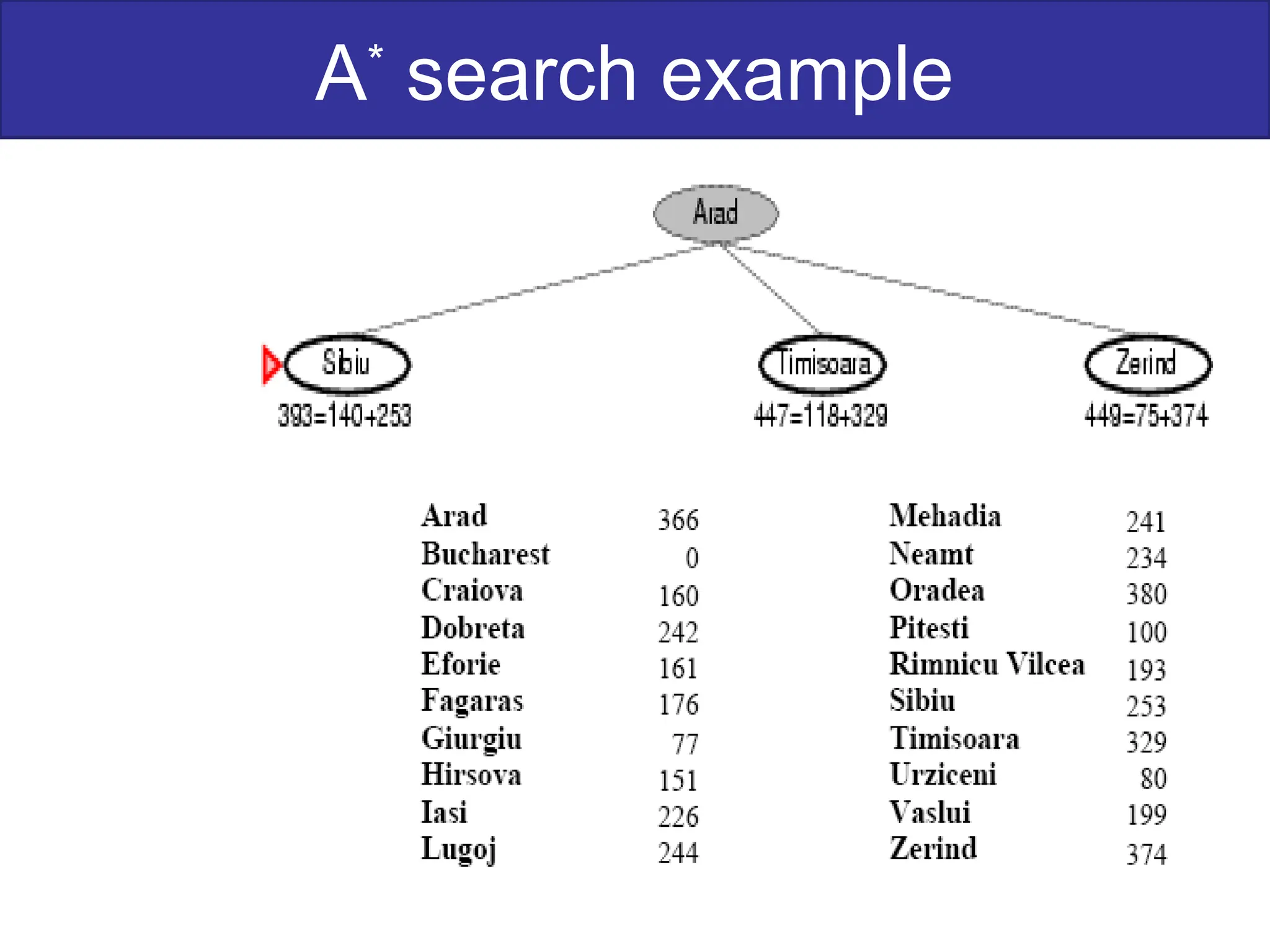
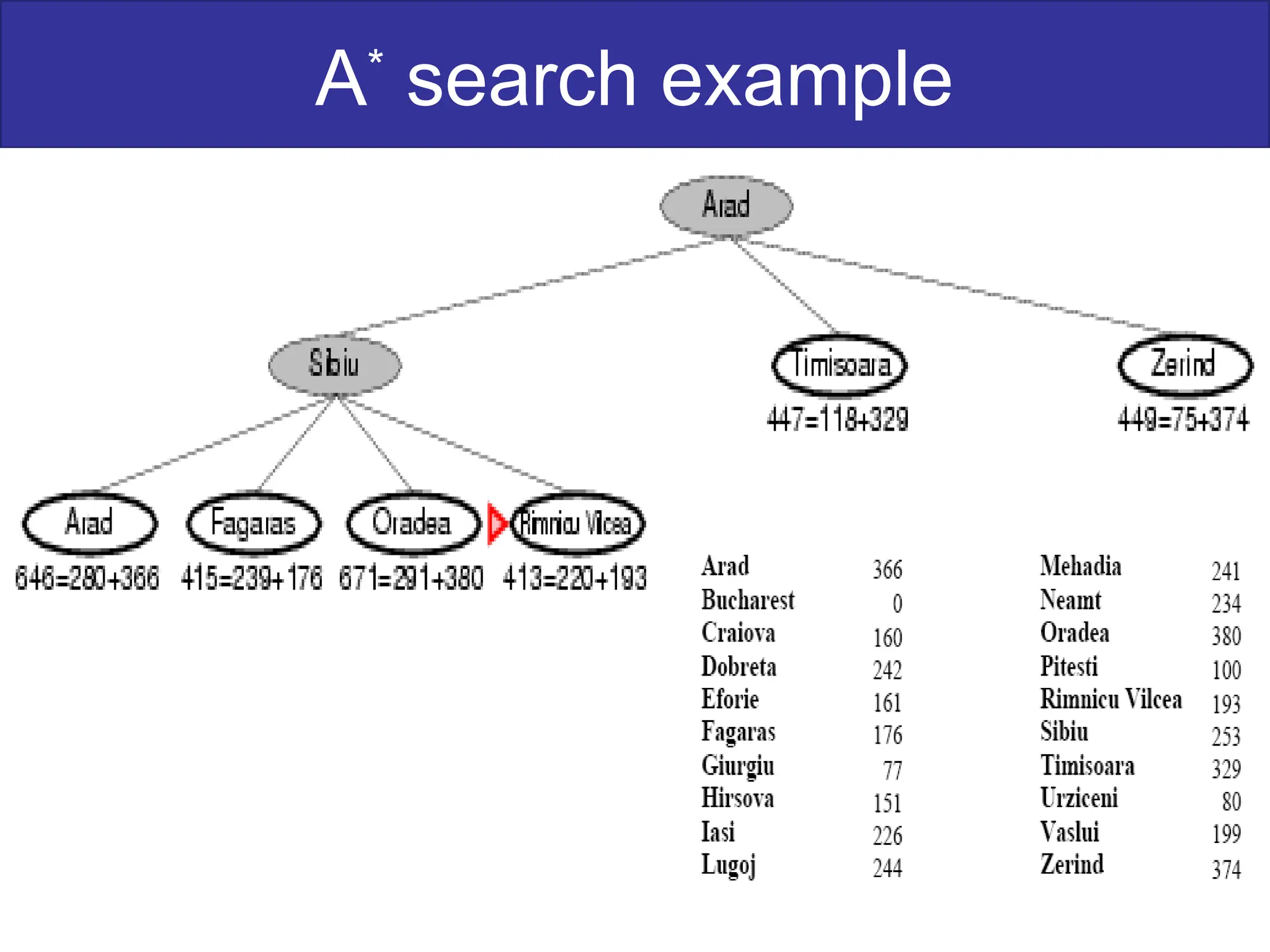
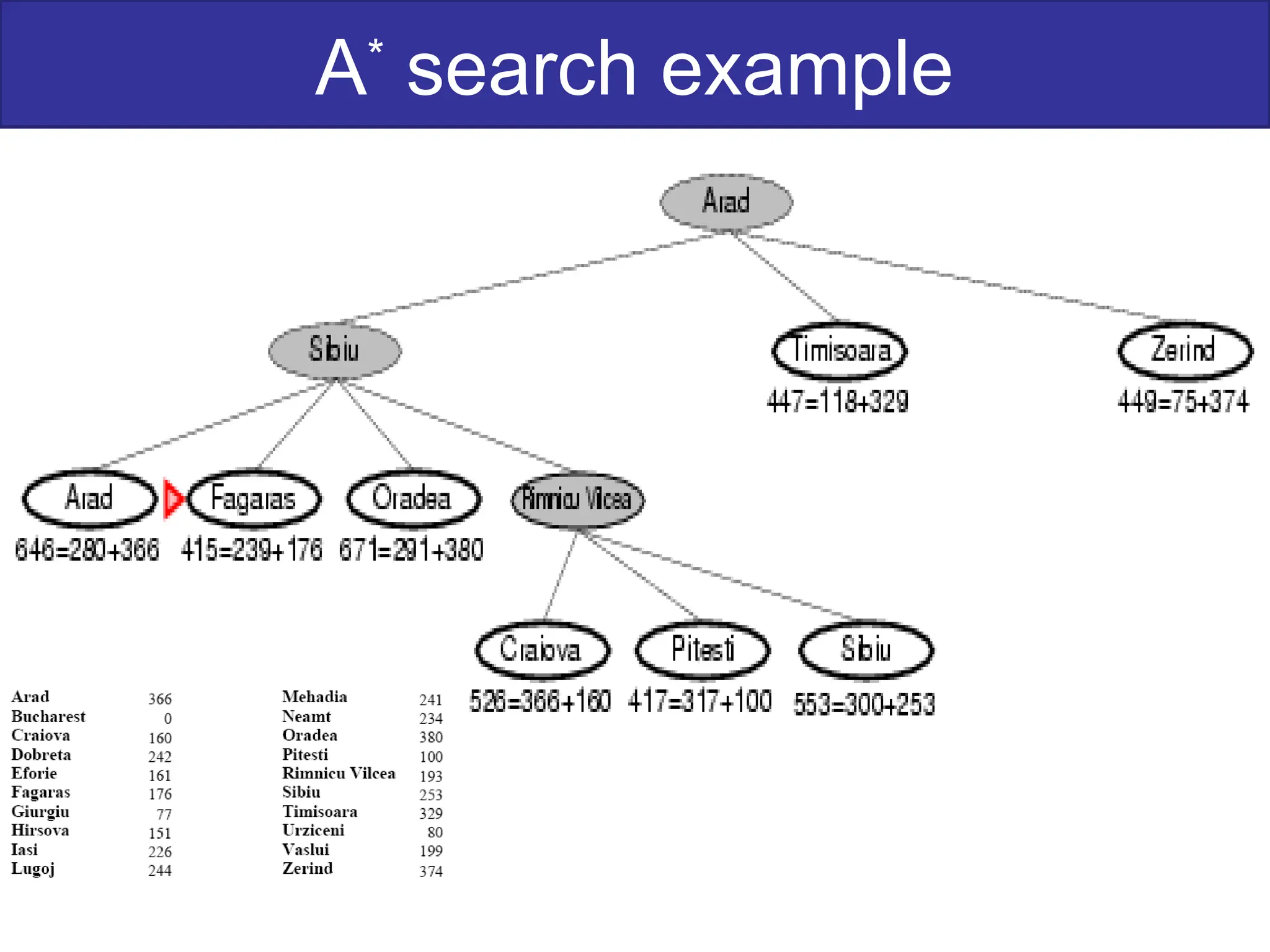
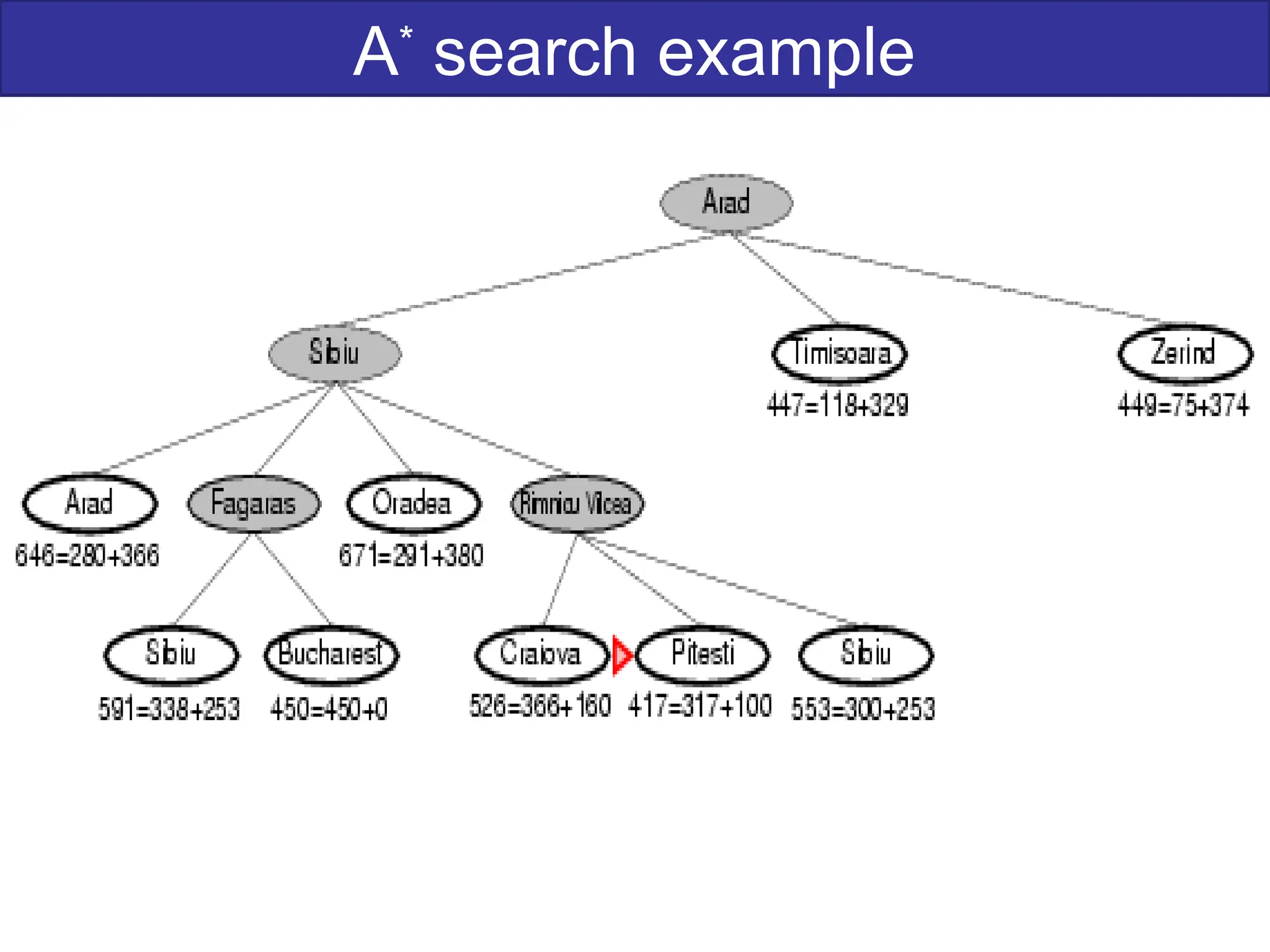
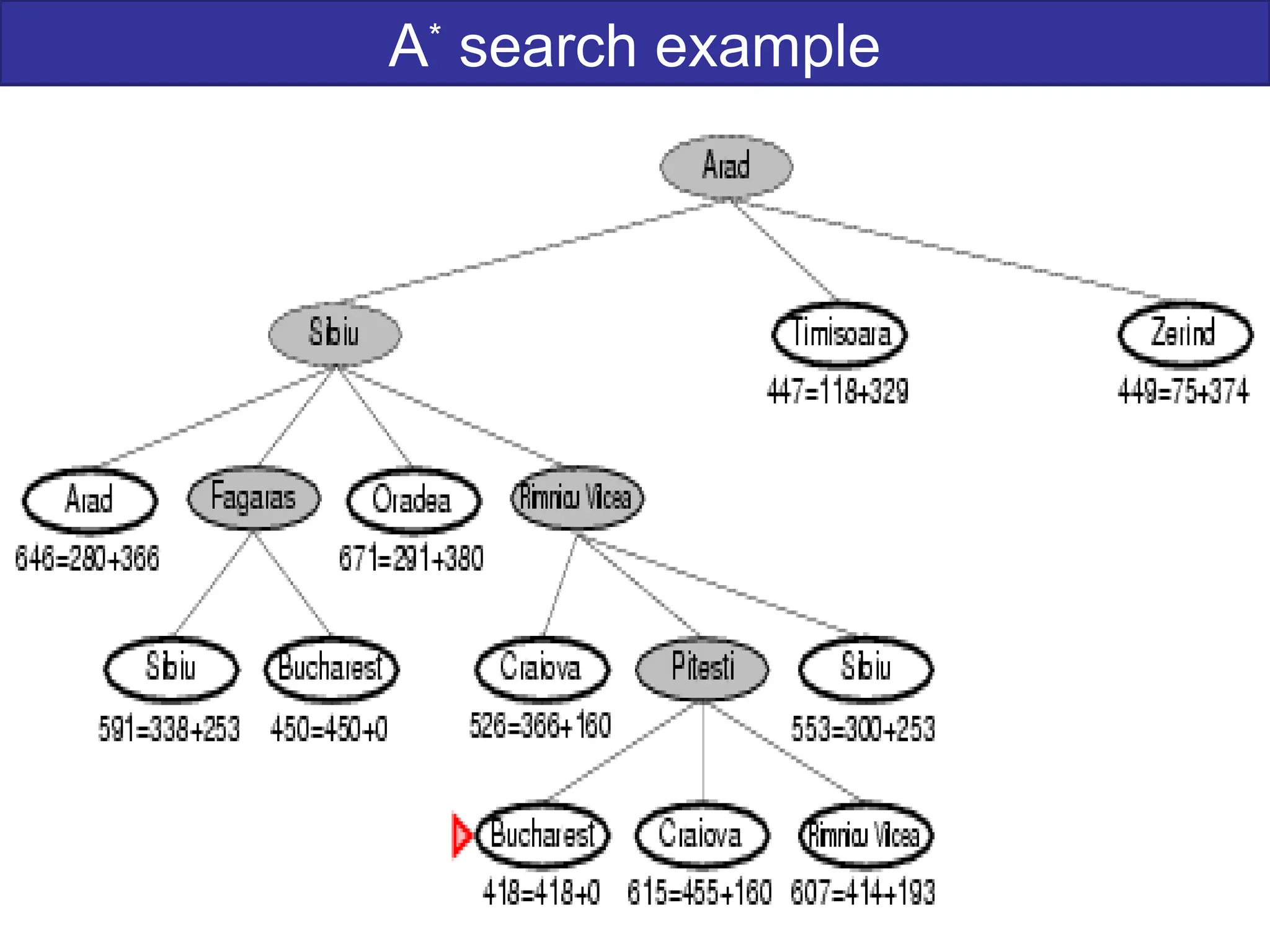
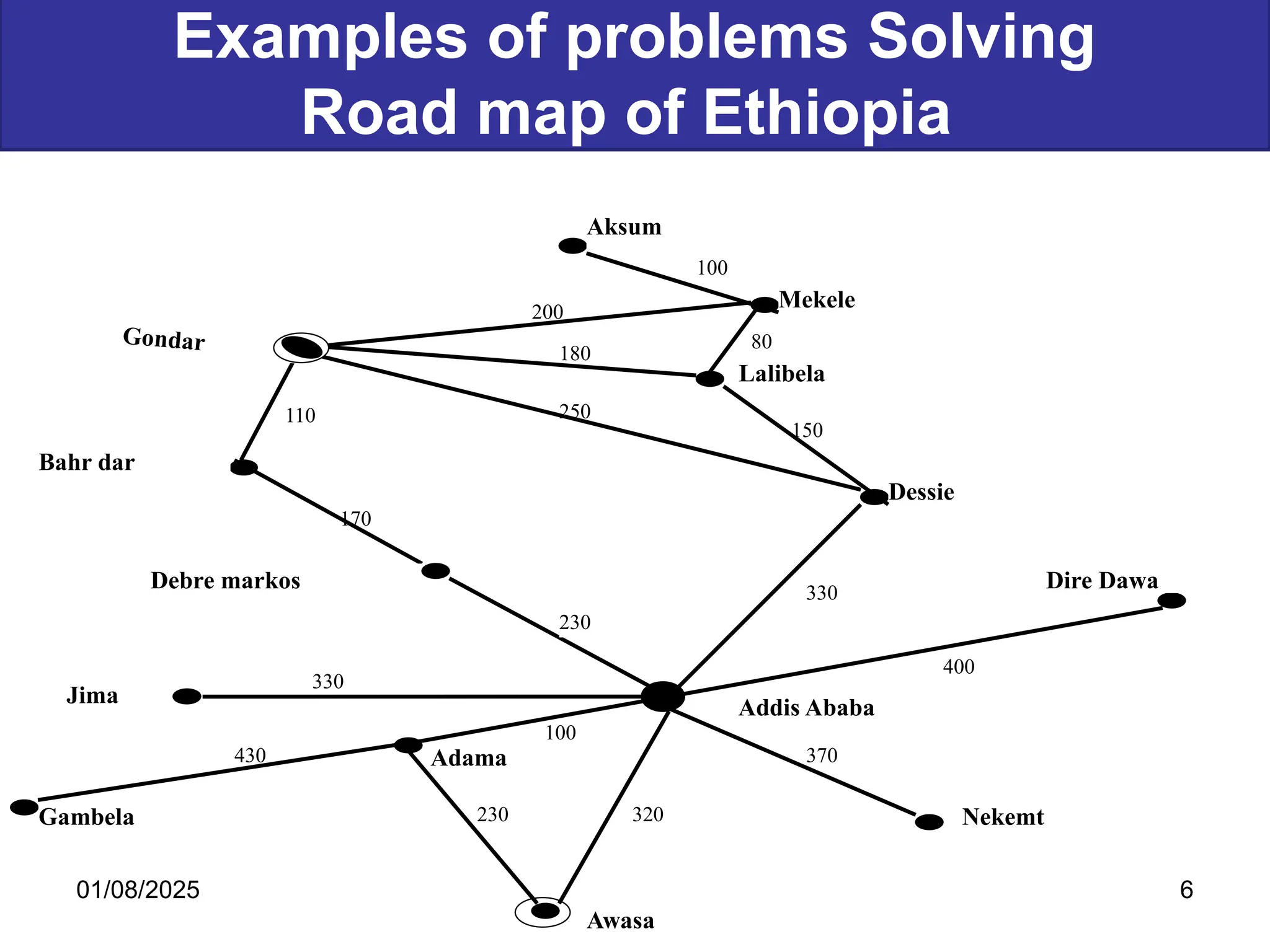
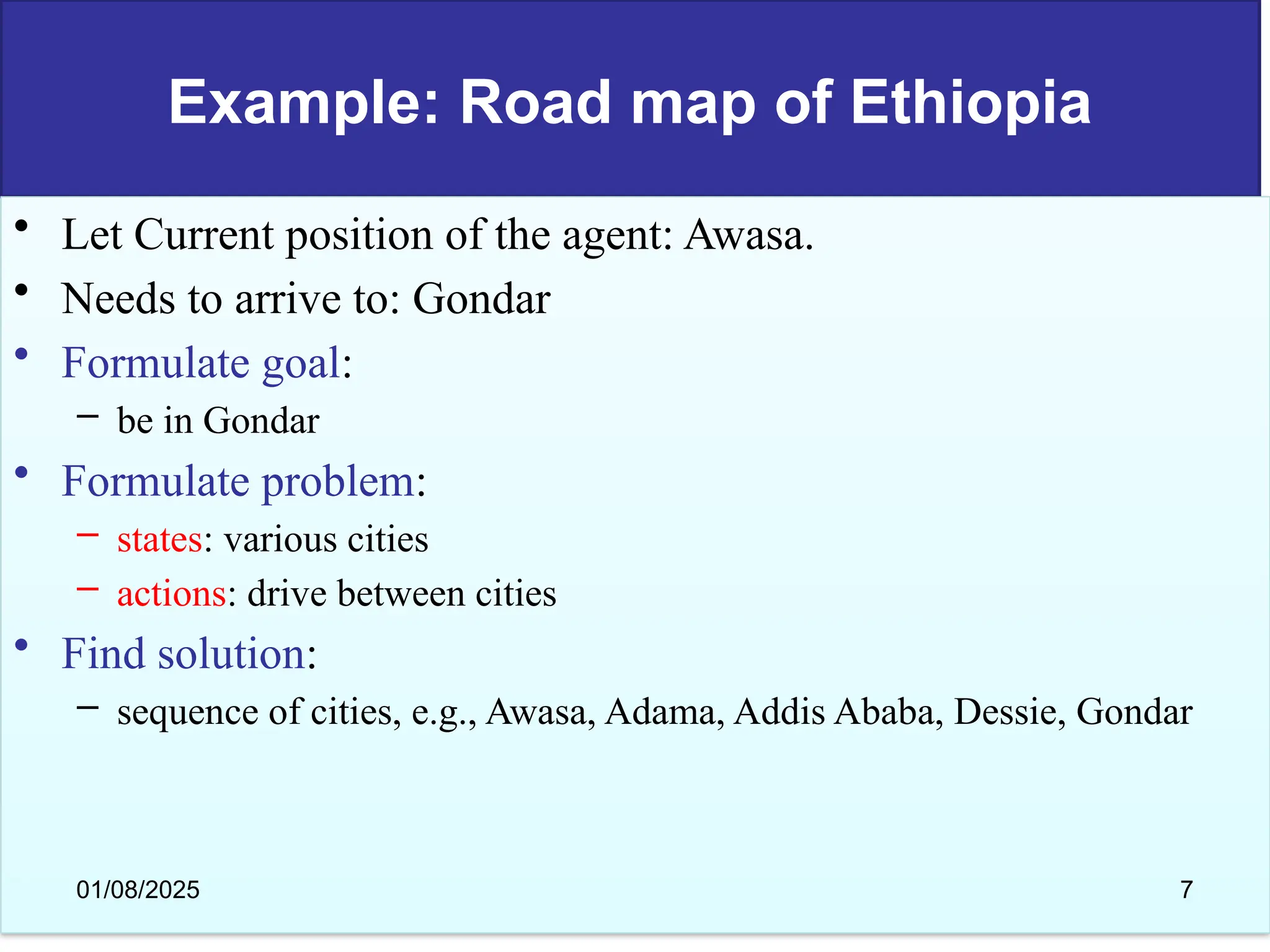
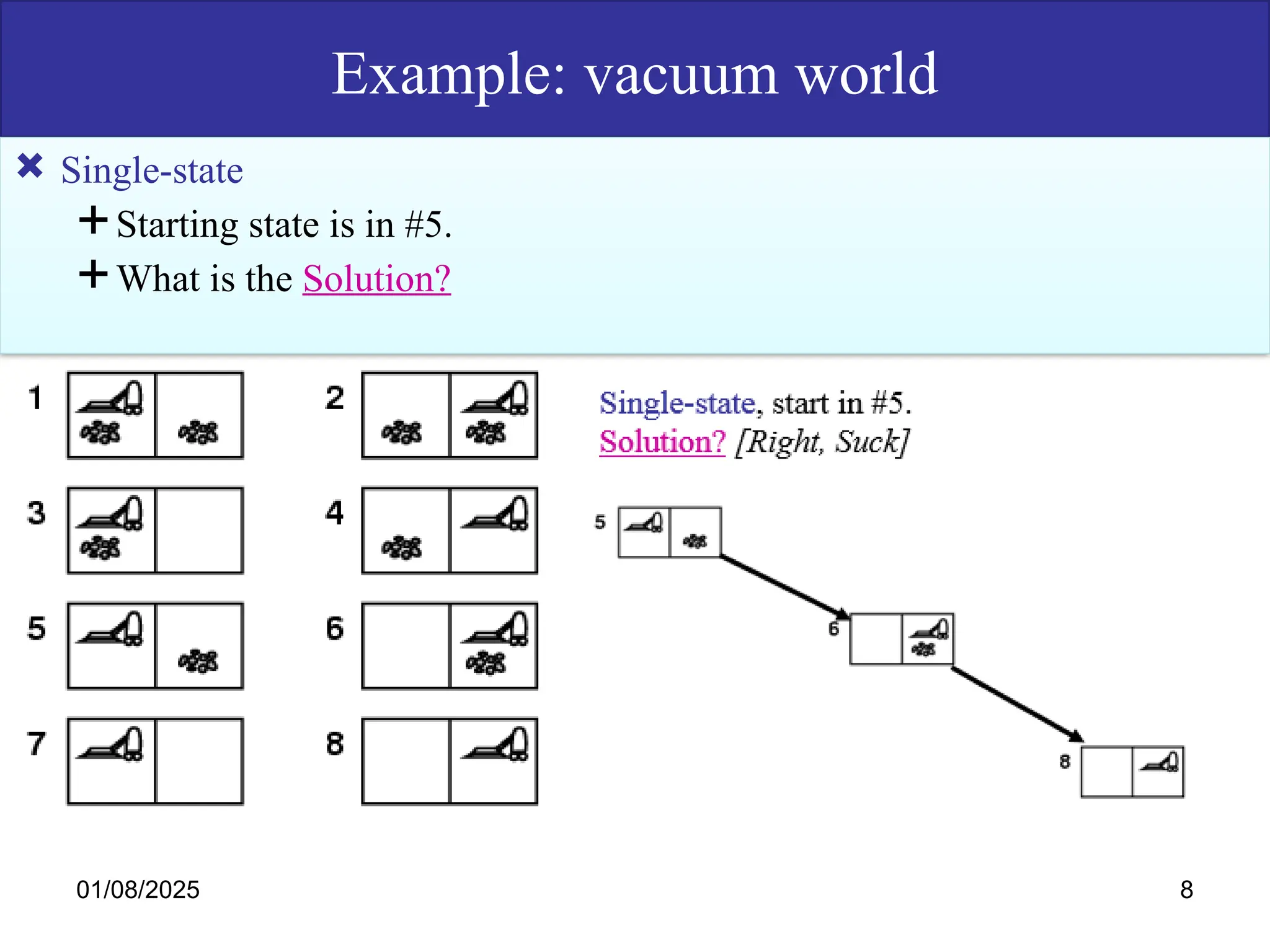
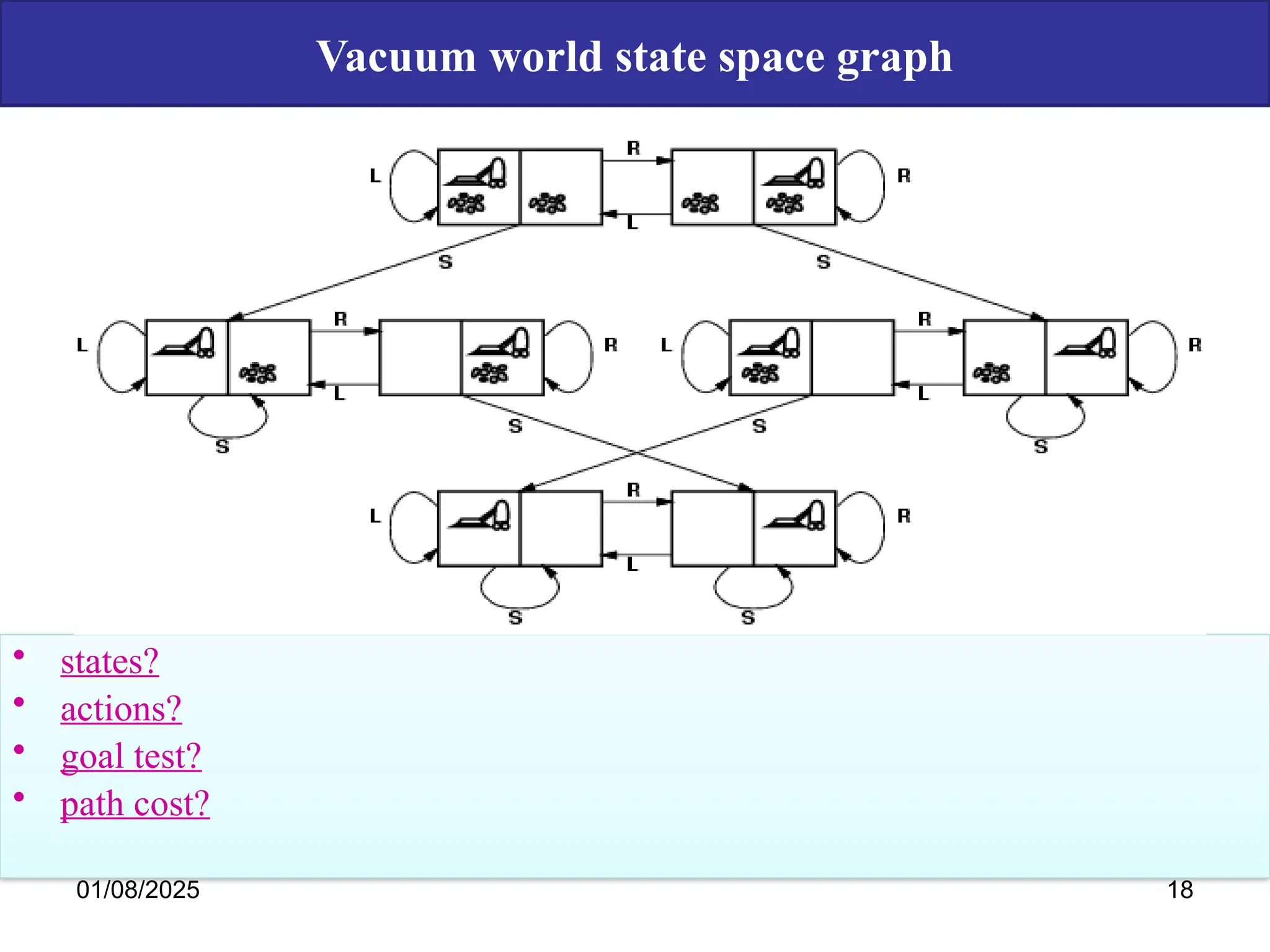
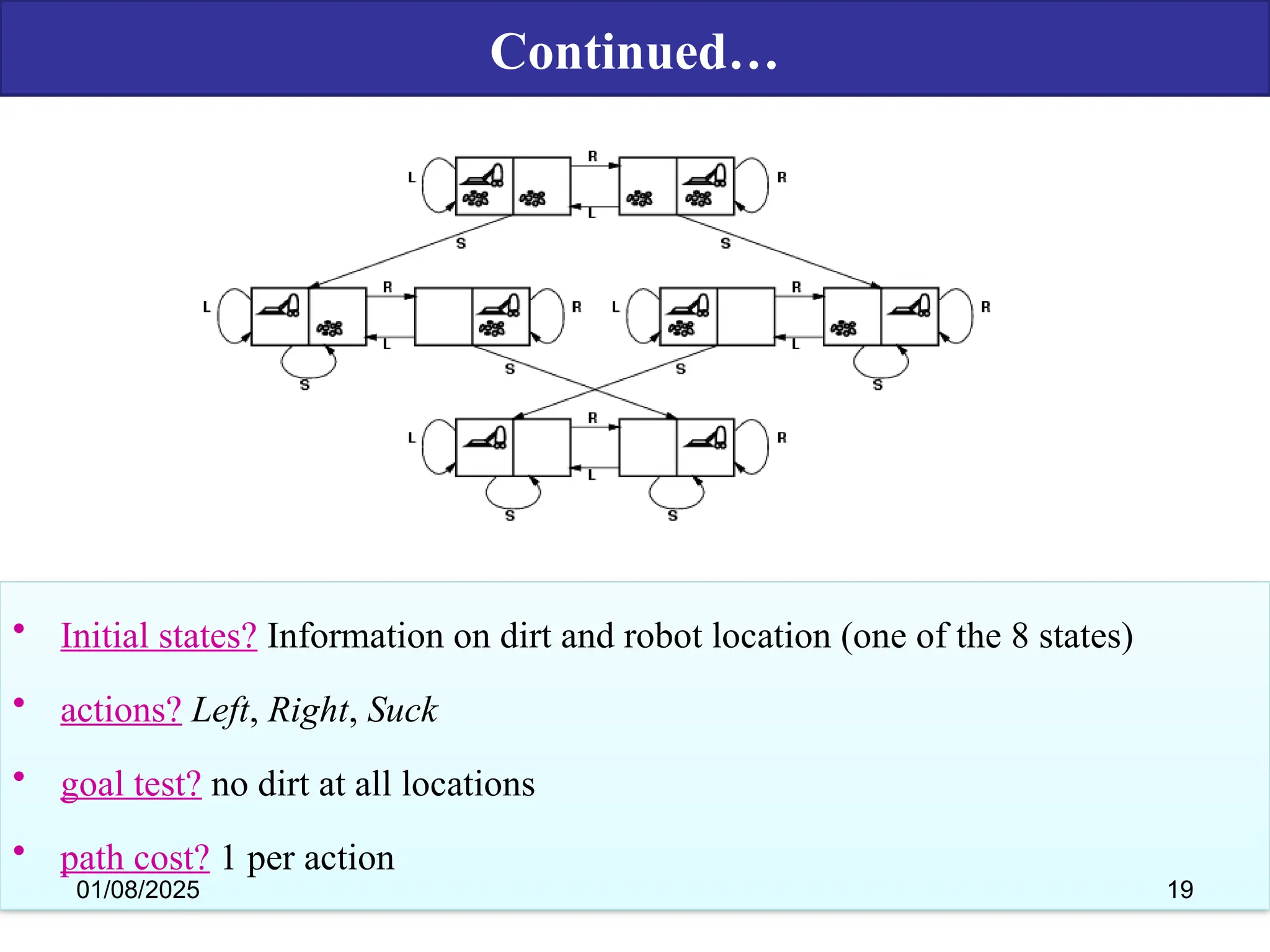
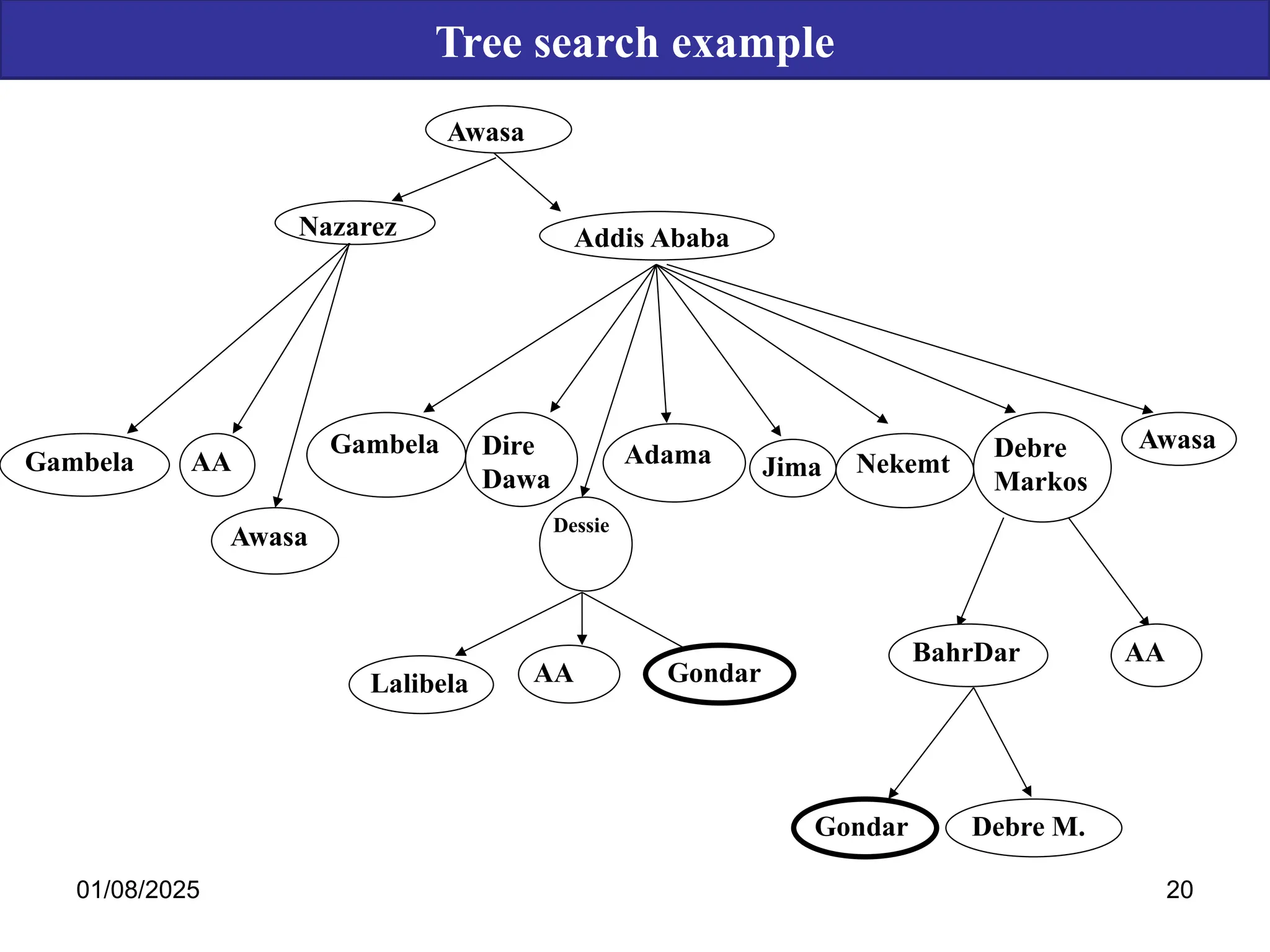
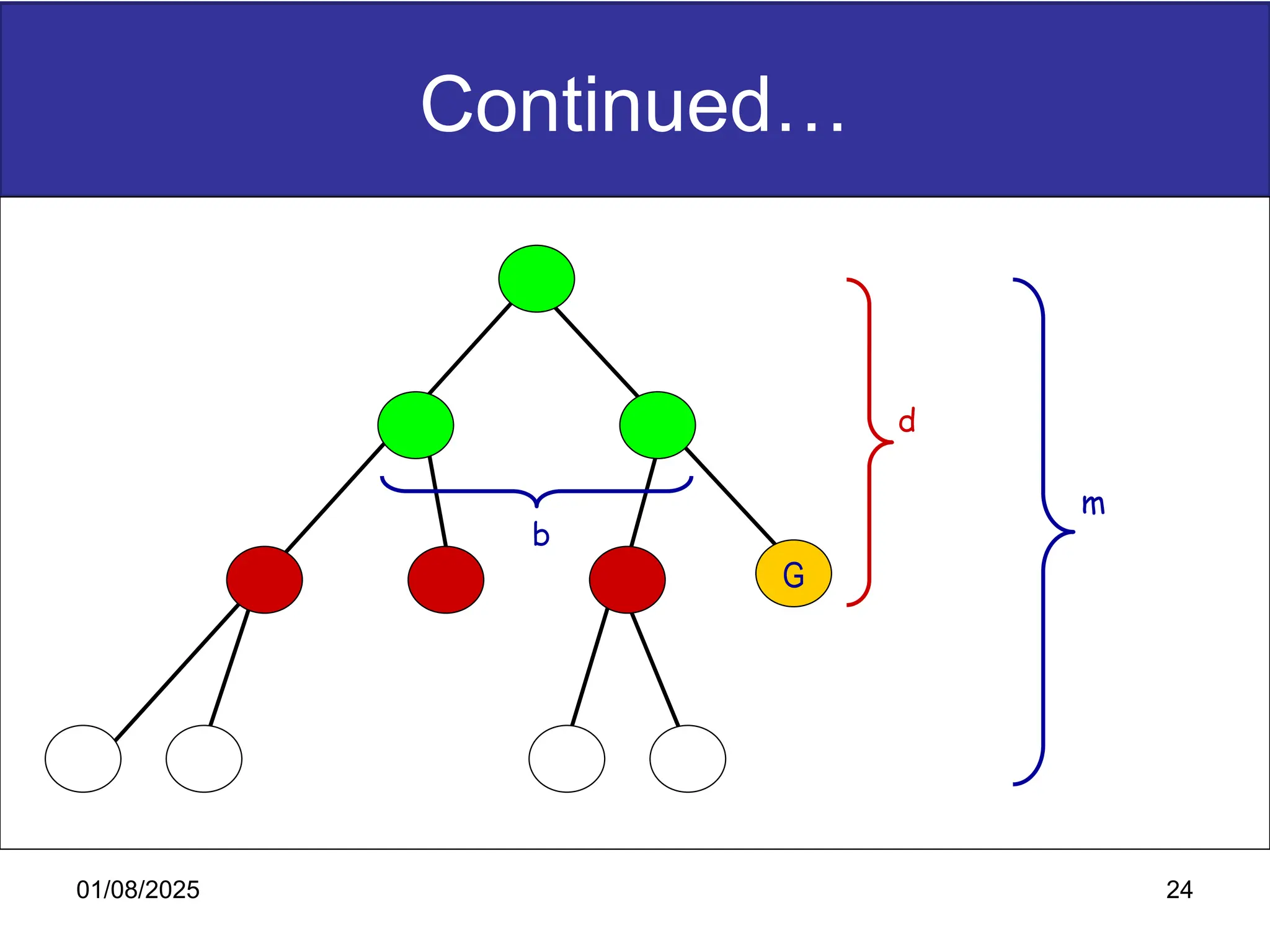
The document discusses goal-based problem-solving agents in artificial intelligence, outlining their functions, processes, and the search strategies utilized to determine optimal action sequences to reach defined goals. It details a five-step process for solving problems, which includes defining the problem, analyzing it, identifying solutions, choosing a solution, and implementation, as well as explaining concepts such as search trees, state space, and various search algorithms. Additionally, it classifies search strategies into uninformed and informed types, emphasizing techniques like breadth-first search, depth-first search, and greedy best-first search.


















![Breadth first search
•Expand shallowest unexpanded node,
–i.e. expand all nodes on a given level of the search
tree before moving to the next level
•Implementation: fringe/open list is a first-in-first-
out (FIFO) queue, i.e.,
•new successors go at end of the queue.
-Is A a goal state?
–Expand: -fringe = [B,C] ,Is B a goal state?
–Expand: fringe=[C,D,E],Is C a goal state?
–Expand: fringe=[D,E,F,G],is D a goal state?
– Pop nodes from the front of the queue
–Then return the final path
–{A,C,G} The solution path is recovered by
following the back pointers starting at the goal
state
01/08/2025
26](https://image.slidesharecdn.com/3problemsolvingusingsearching-250108195426-1ed6687a/75/chapter-3-Problem-Solving-using-searching-pptx-26-2048.jpg)