Downloaded 46 times















This document discusses computational complexity and analyzing the running time of algorithms. It defines big-O notation, which is used to classify algorithms according to their worst-case performance as the problem size increases. Examples are provided of algorithms with running times that are O(1), O(log N), O(N), O(N log N), O(N^2), O(N^3), and O(2^N). The growth rates of these functions from slowest to fastest are also listed.
Introduction to computational complexity, running time analysis, leading terms, and performance of algorithms.
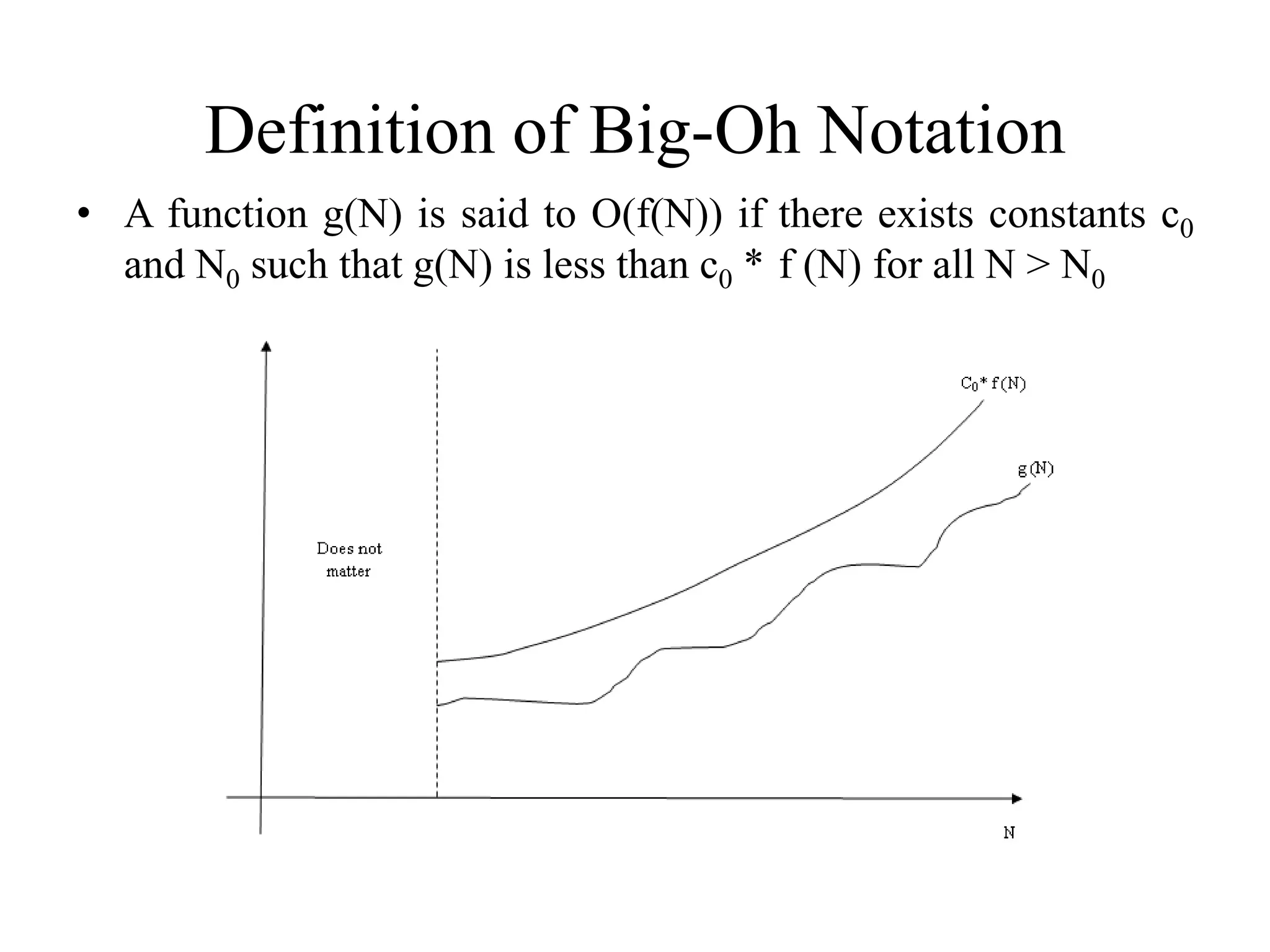
Definition and examples of Big-Oh notation, illustrating how to classify functions regarding growth rates.
Examines a specific problem's growth rate comparison and lists functions in increasing order of growth rate.
Exemplifies algorithm complexities and the experimental comparison of algorithms with sample data.
Shows a sample C program that measures execution time including necessary header files.
Final references, open floor for questions, and expressions of gratitude.














