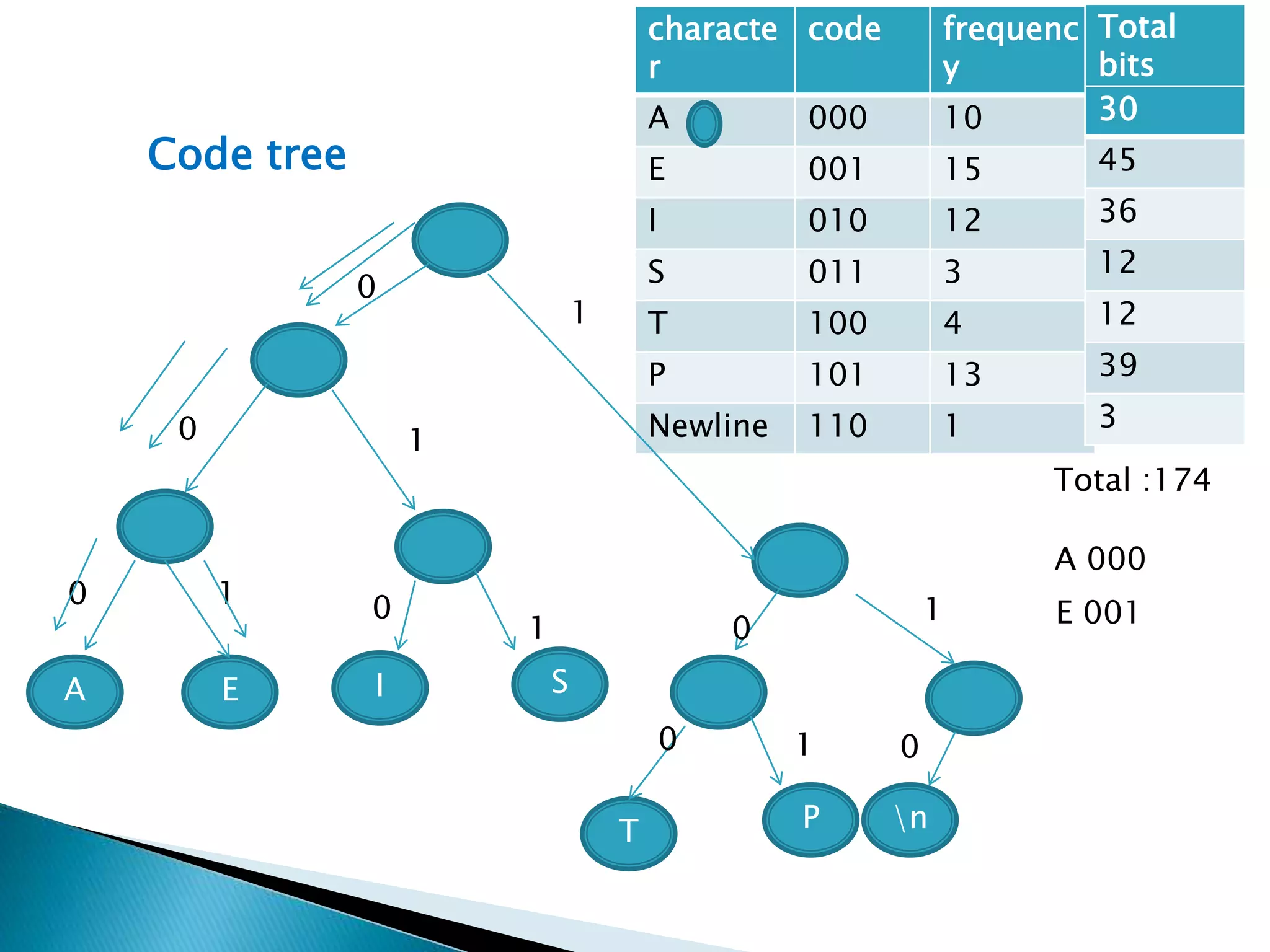
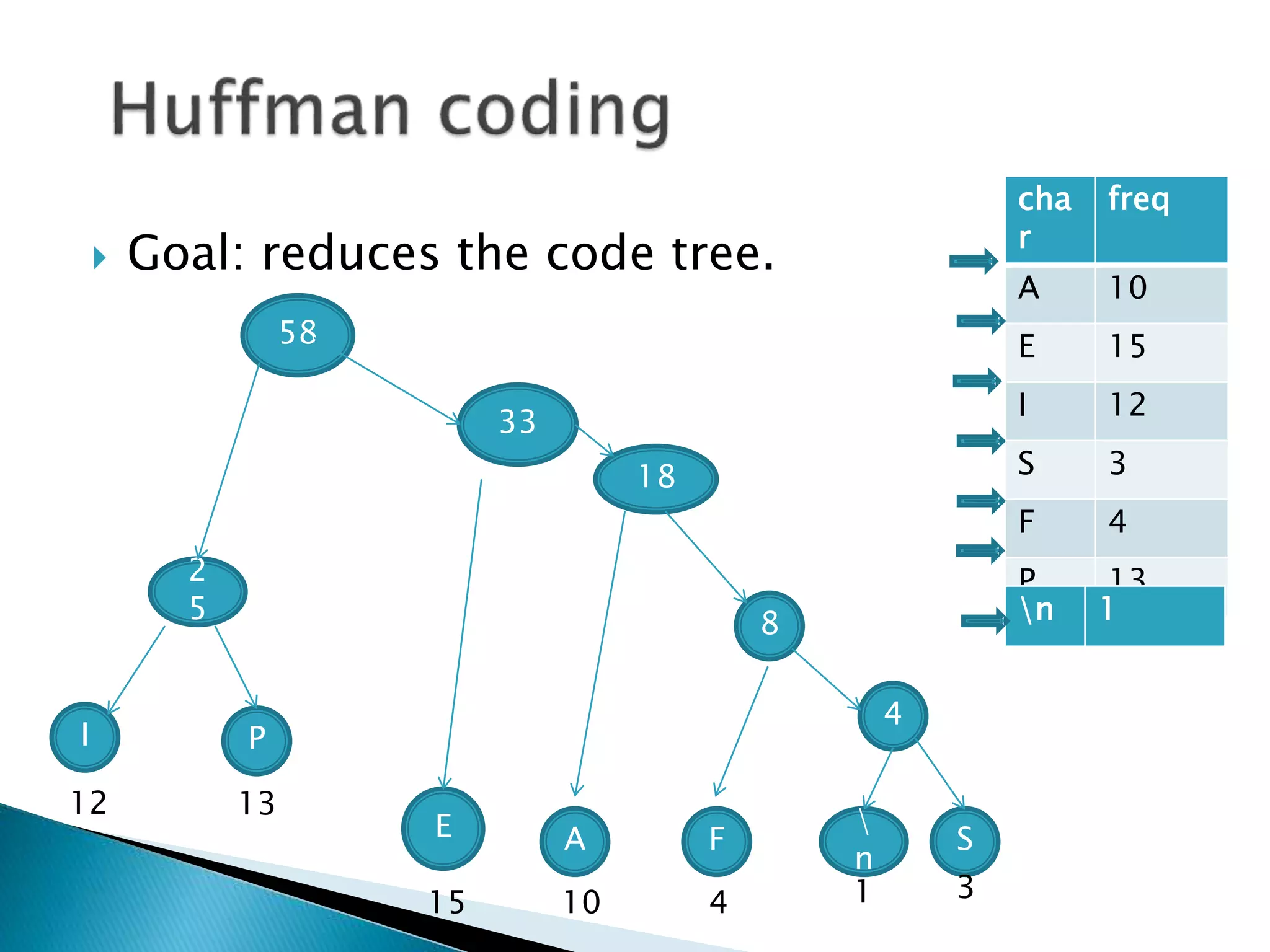
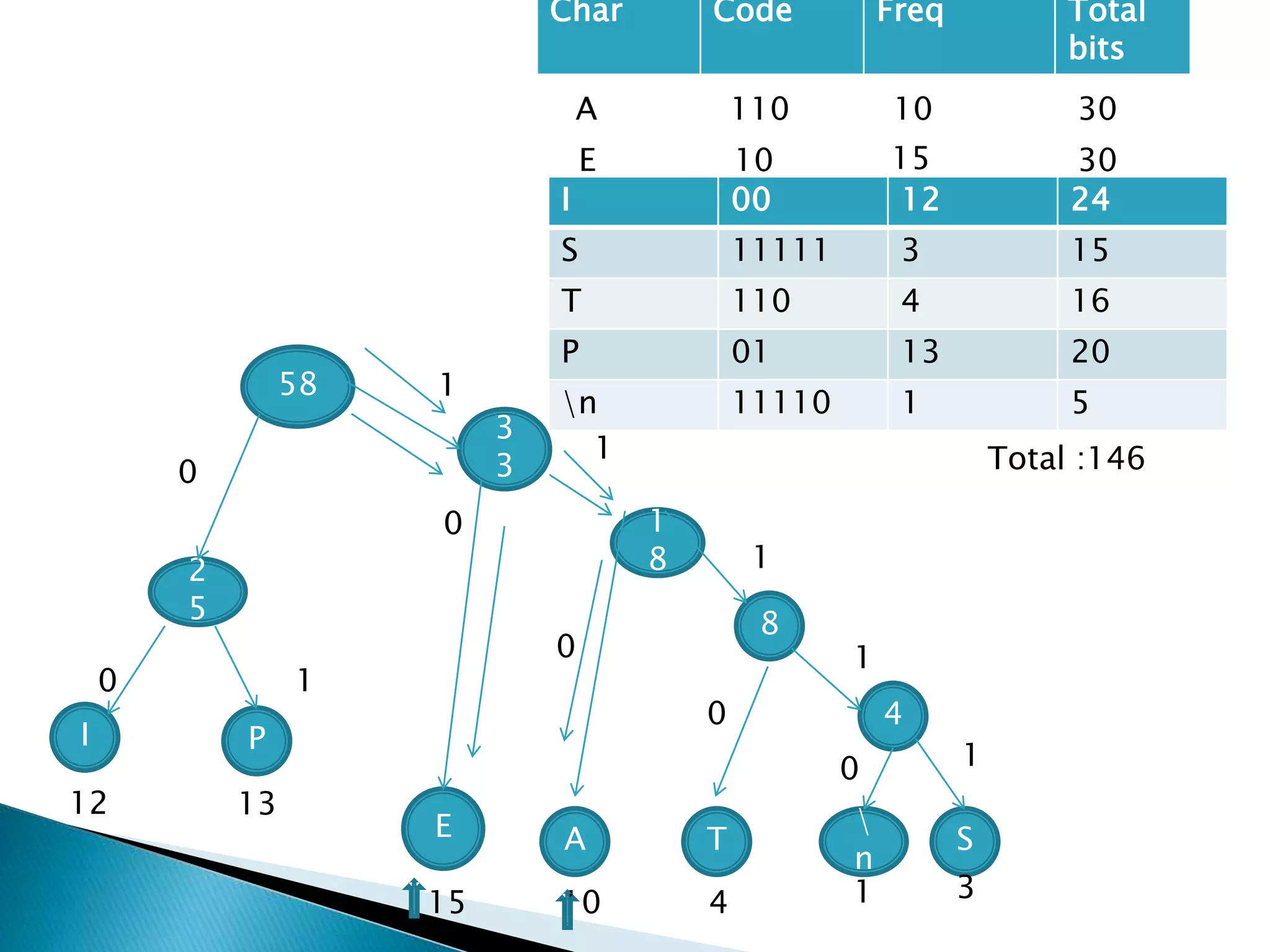
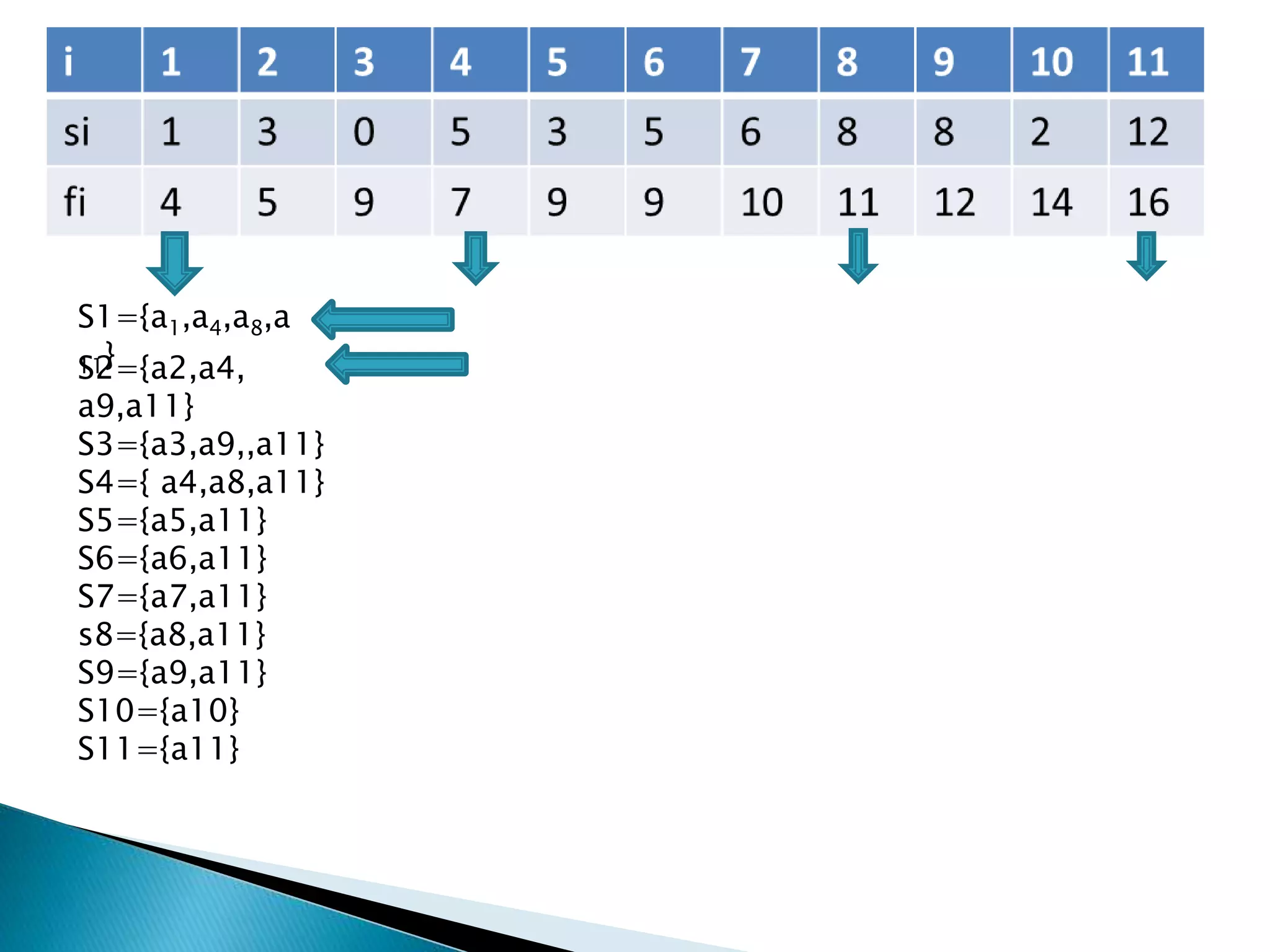
The document discusses various algorithms for merging files efficiently, highlighting different strategies such as two-way and k-way merging, and calculating their associated costs. It also covers greedy algorithms, their applications in activity selection, and the limitations of the greedy approach, particularly in the 0-1 knapsack problem versus the fractional knapsack problem. The text references key sources and provides examples to illustrate concepts.

![ Let us consider that you have an array F with size
n.
F[i] contains the size of ith file
We want merge that file into one single file.
What could be the best possible solution for
that….?
1) A and B are two files with sizes and then time
complexity of merging it is 0(m+n)
Eg: F={10,5,100,50,20,15}
N=6](https://image.slidesharecdn.com/greedyalgorithm-200319171637/75/computer-operating-system-Greedy-algorithm-2-2048.jpg)







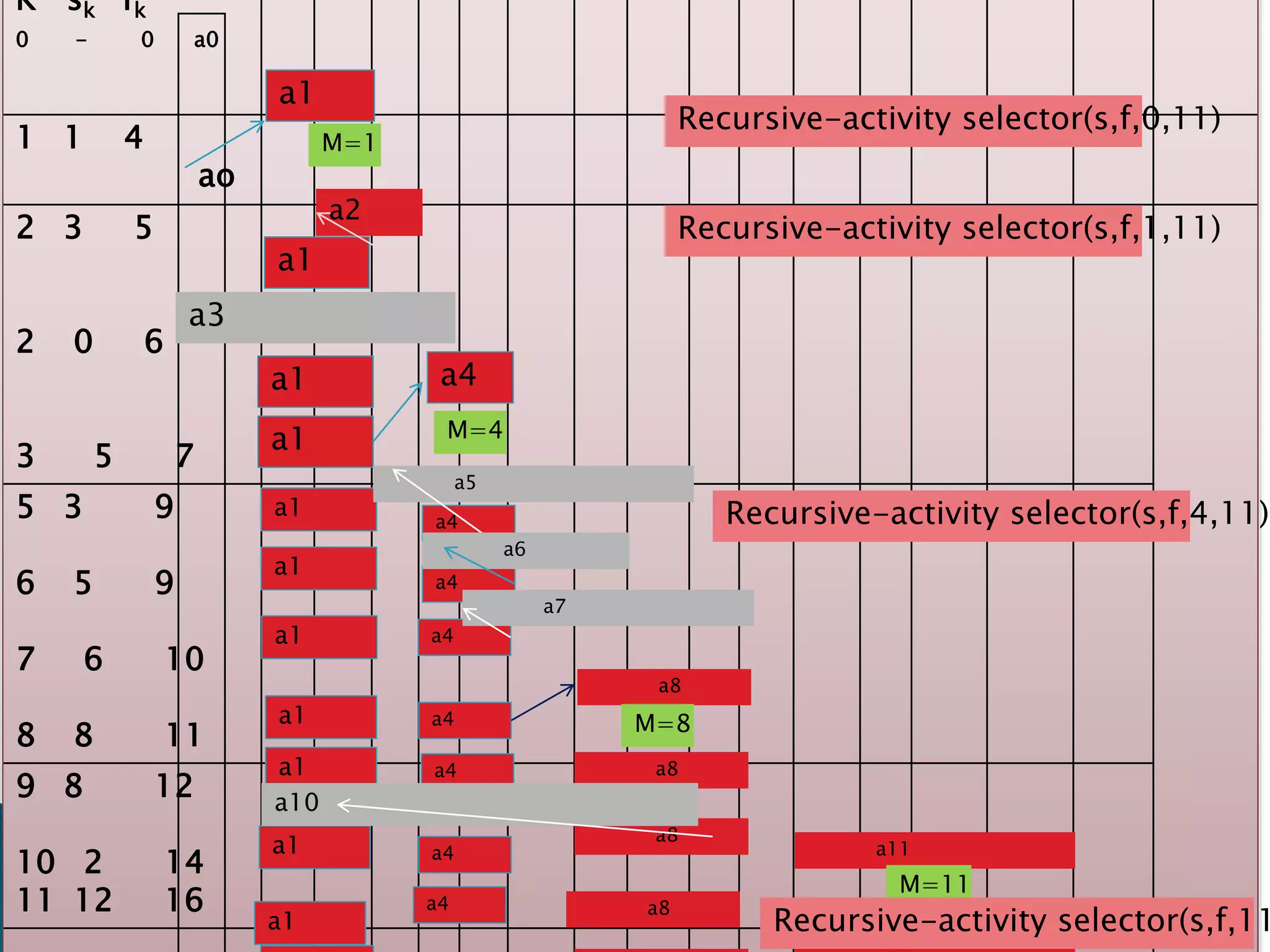
![ m=k+1
While m≤n and s[m]<f[k]
M=m+1
If m≤n
return{am}URECURSIVE-ACTIVITY-SELECTOR(
s, f, k, n)
Else return ∅](https://image.slidesharecdn.com/greedyalgorithm-200319171637/75/computer-operating-system-Greedy-algorithm-11-2048.jpg)

![ n=s.length
A={a1}
K=1
For m=2 to n
If s[m]≥f[k]
A=AU{am}
K=m
Return A](https://image.slidesharecdn.com/greedyalgorithm-200319171637/75/computer-operating-system-Greedy-algorithm-14-2048.jpg)