Downloaded 62 times
Uploaded byKasun Ranga Wijeweera
Convex Hull Algorithms
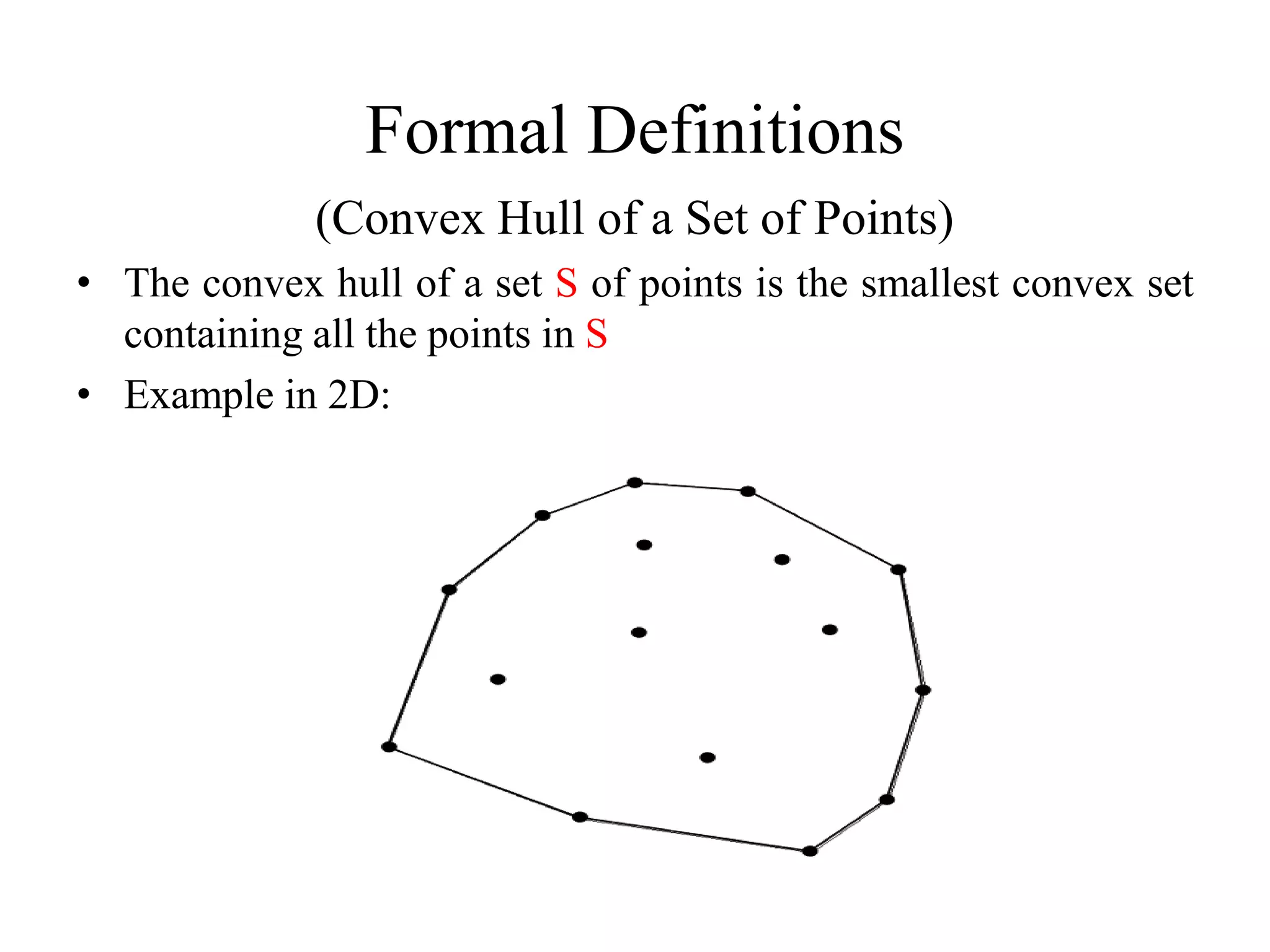
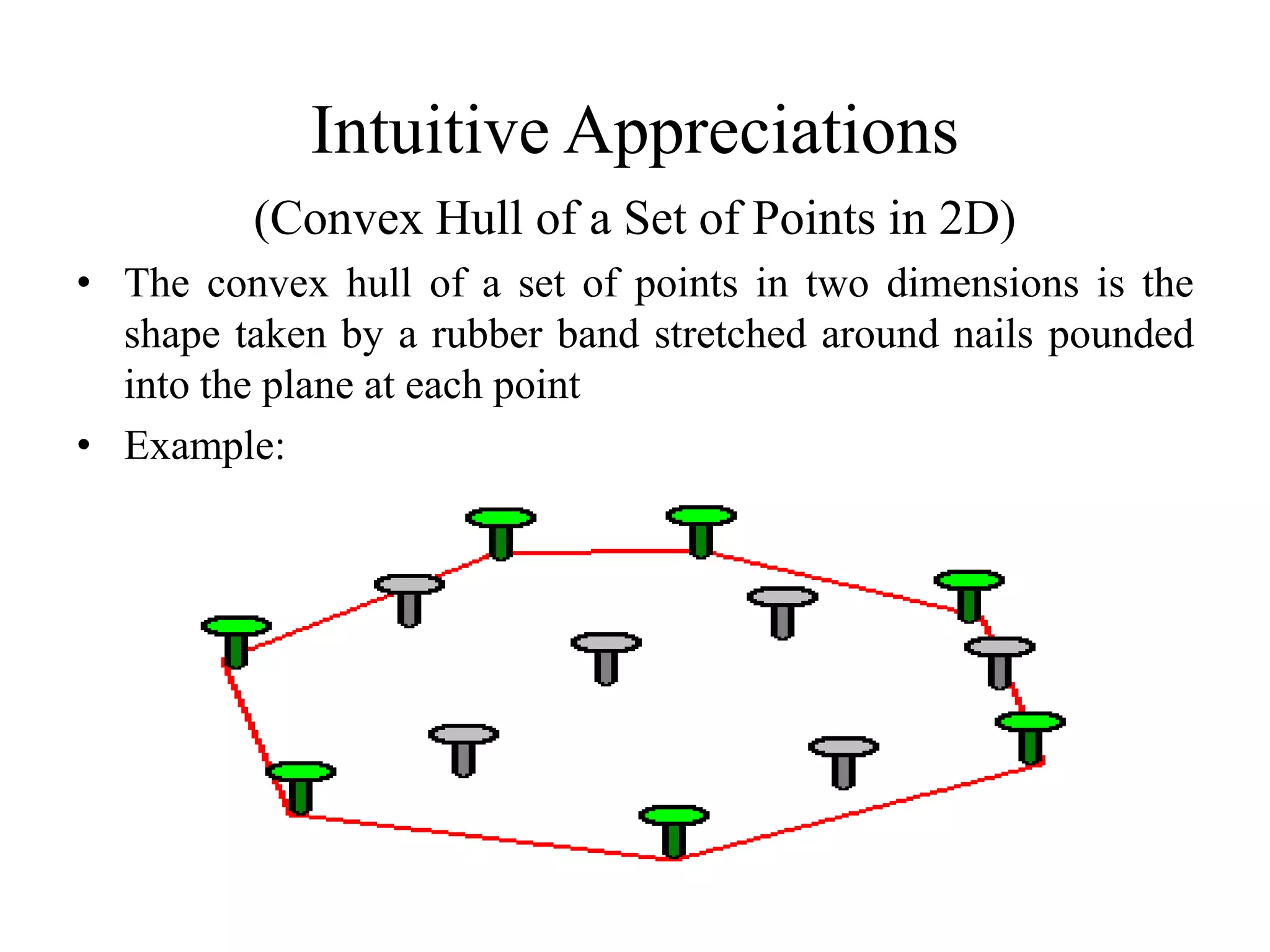
This document discusses convex hull algorithms. It defines a convex set as one where any line segment between two points in the set is also contained in the set. The convex hull of a set of points is the smallest convex set containing those points. Intuitively, in 2D the convex hull is the shape formed by stretching a rubber band around nails at each point, and in 3D it is the shape formed by stretching plastic wrap tightly around the points. The document then lists and describes several existing convex hull algorithms and provides an overview of an interior points algorithm that identifies non-extreme points based on whether they lie within triangles formed by other points.
In this document
Powered by AI
An introduction to Convex Hull Algorithms presented by Kasun Ranga Wijeweera.
Formal definition of a convex set, indicating that a set S is convex if any segment between two points in S lies in S.
Definition of the convex hull, defined as the smallest convex set that contains all points in a set S.
Intuition behind the convex hull in 2D; compared to a rubber band stretched around points.
Intuition behind the convex hull in 3D; likened to plastic wrap tightly enclosing the points.
Convex hull algorithms can be applied to collision avoidance in various fields.
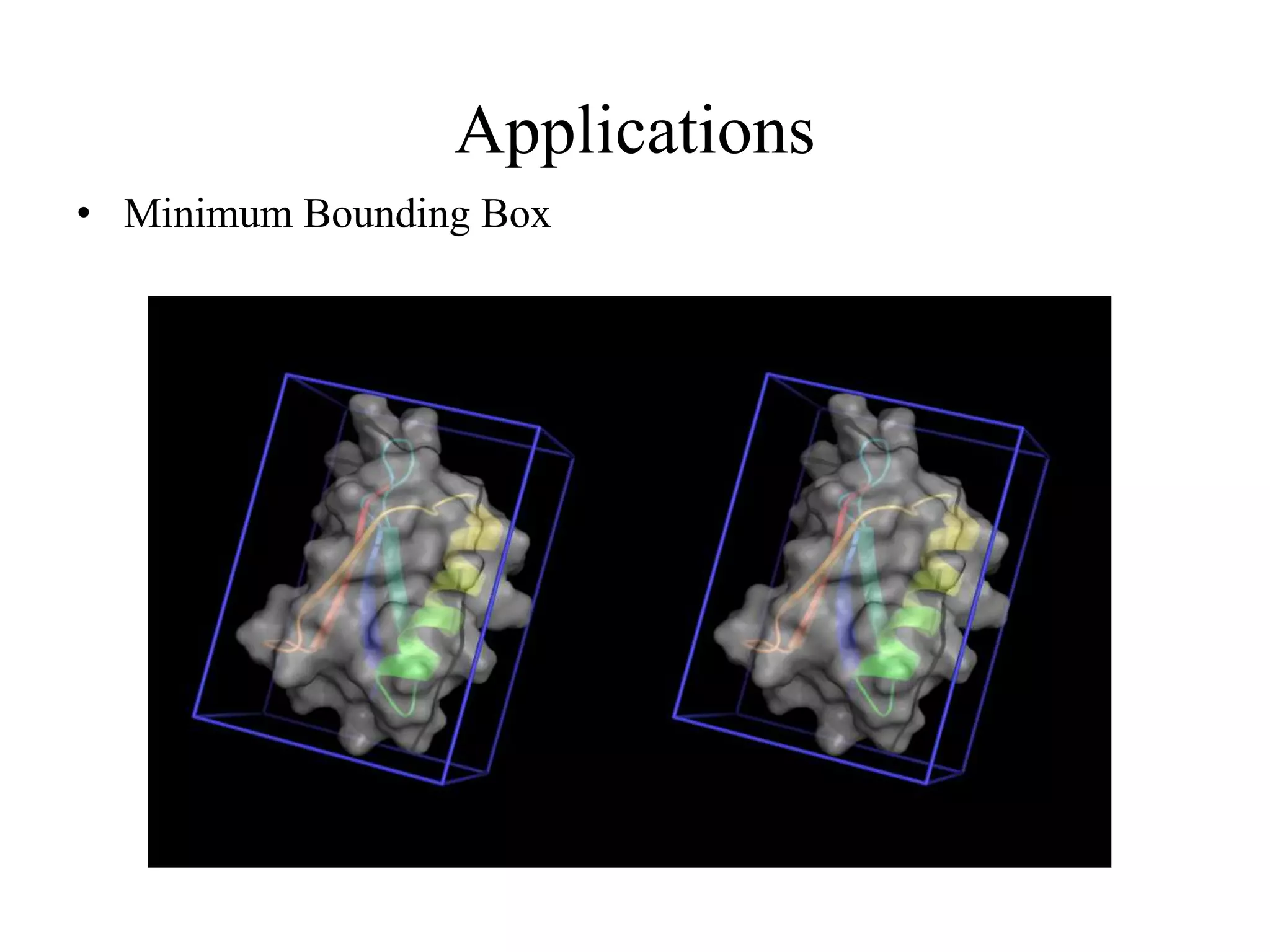
Minimum bounding box applications are discussed as one of the uses of convex hull algorithms.
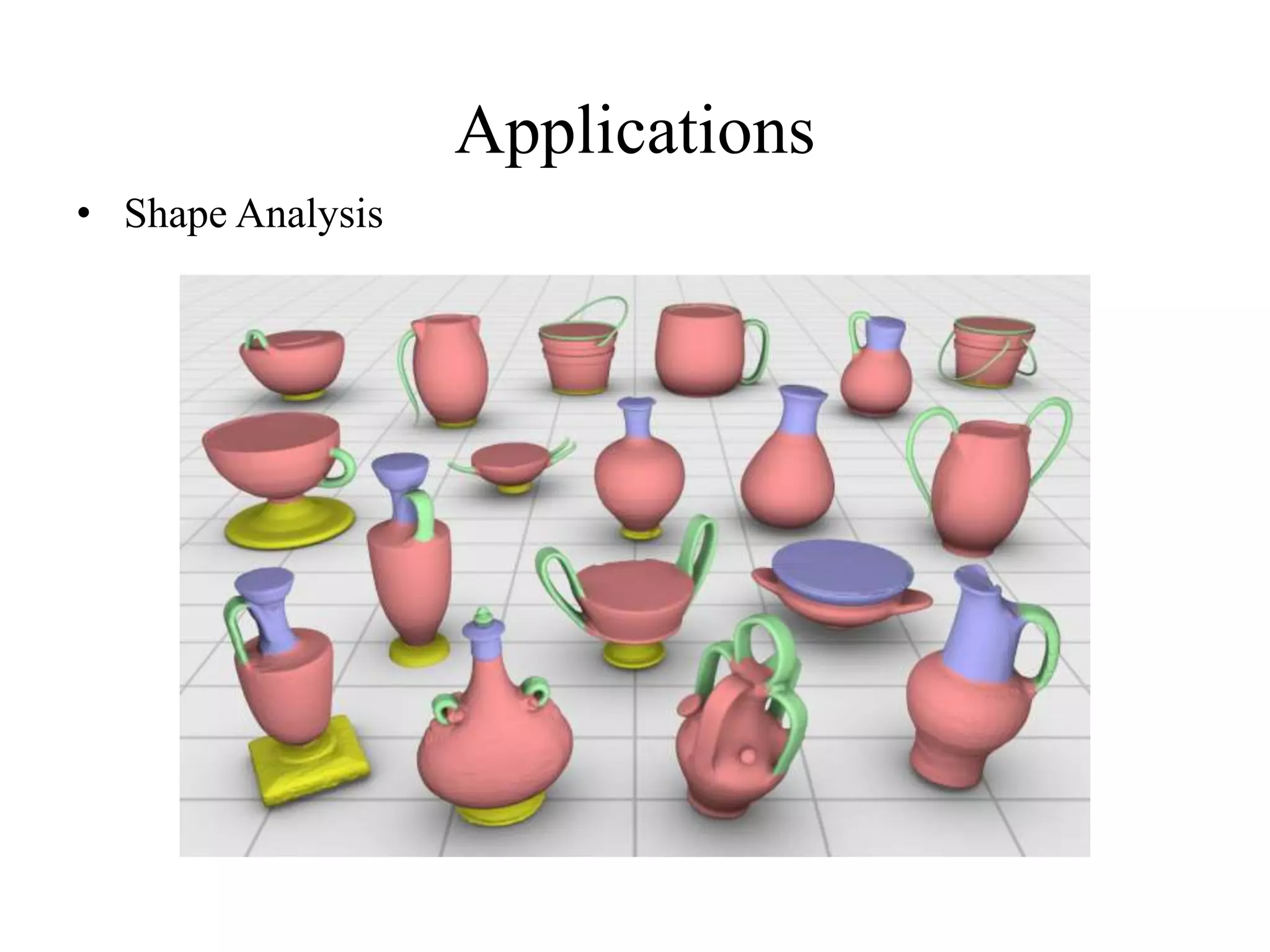
Shape analysis as a significant application area for convex hull algorithms.
List of existing convex hull algorithms, including Gift Wrapping, Graham Scan, Quick Hull, and others up to 1996.
Introduction to the interior points algorithm, detailing conditions for a non-extreme point.
Algorithm pseudocode outlining how to determine non-extreme points based on triangle conditions.
An invitation for questions from the audience to clarify any points discussed.
Wrapping up the presentation with a thank you note from the presenter.
More Related Content
![On the Convex Layers of a Planer Dynamic Set of Points [Short Version]](https://cdn.slidesharecdn.com/ss_thumbnails/mphillayersmod1f-180628051342-thumbnail.jpg?width=600ounds&width=560&fit=bounds)
![Assignment for Factory Method Design Pattern in C# [ANSWERS]](https://cdn.slidesharecdn.com/ss_thumbnails/assingment1answers-200420114633-thumbnail.jpg?width=600ounds&width=560&fit=bounds)
Convex Hull Algorithms
- 1. Convex Hull Algorithms Kasun Ranga Wijeweera (krw19870829@gmail.com)
- 2. Formal Definitions (Convex Set) • A set S is convex if x in S and y in S implies that the segment xy is a subset of S • Example in 2D:
- 3. Formal Definitions (Convex Hull of a Set of Points) • The convex hull of a set S of points is the smallest convex set containing all the points in S • Example in 2D:
- 4. Intuitive Appreciations (Convex Hull of a Set of Points in 2D) • The convex hull of a set of points in two dimensions is the shape taken by a rubber band stretched around nails pounded into the plane at each point • Example:
- 5. Intuitive Appreciations (Convex Hull of a Set of Points in 3D) • The boundary of the convex hull of points in three dimensions is the shape taken by plastic wrap stretched tightly around the points • Example:
- 6.
- 7.
- 8.
- 9. Existing Convex HullAlgorithms • Gift Wrapping (1970) • Graham Scan (1972) • Quick Hull (1977) • Divide and Conquer (1977) • Monotone Chain (1979) • Incremental (1984) • Marriage before Conquest (1986) • Chan (1996)
- 10. Interior Points Algorithm Basedon the following Lemma A point is non-extreme if and only if it is inside some (closed) triangle whose vertices are points of the set and is not itself a corner of that triangle
- 11. Interior Points Algorithm Algorithm:INTERIOR POINTS for each i do for each j != i do for each k != i != j do for each l != k != i != j do if p(l) in Triangle{ p(i), p(j), p(k) } then p(l) is non-extreme
- 12.
- 13.