Convex hulls & Chan's algorithm

CONVEX HULLS
Chan's optimal output sensitive
algorithms for convex hulls
Alberto Parravicini
Université libre de Bruxelles
December 15, 2016

What's on the menu?
→ Basic notions
2

What's on the menu?
→ Basic notions
→ Algorithms for convex hulls
2

What's on the menu?
→ Basic notions
→ Optimal 2D algorithm
2

What's on the menu?
→ Basic notions
2

Crash course on convex hulls
A convex set S is a set in which, ∀ x, y ∈ S, the
segment xy ⊆ S.
Given a set of points P in d dimensions, the
Convex Hull CH(P) of P is:
4

segment xy ⊆ S.
→ the minimal convex set containing P.
4

segment xy ⊆ S.
→ the minimal convex set containing P.
→ the union of all convex combinations of
points in P, i.e. the points CH(P) are s.t.
|P|
∑
i=1
wi · xi, ∀xi ∈ P, ∀wi : wi ≥ 0 and
|P|
∑
i=1
wi = 1
4

Output sensitive algorithm
The complexity of an output-sensitive
algorithm is a function of both the input size
and the output size.
5

Jarvis's march
→ Core idea: given an edge pq of the convex
hull, the next edge qr to be added will
maximize the angle ∠∠∠pqr
7

Jarvis's march
→ At each step we scan all the n points.
7

Jarvis's march
→ How many steps? h, size of the hull.
7

Jarvis's march
→ How many steps? h, size of the hull.
→ Complexity: O(nh)
7

One step, visually
Figure: A step of the Jarvis March. The red line is the next
segment that will be added to the hull.
8

Jarvis's march
Algorithm 1: Jarvis March
Input: a list S of bidimensional points.
Output: the convex hull of the set, sorted counterclockwise.
hull =[]
x0 = the leftmost point.
hull.push(x0)
Loop hull.last() != hull.first()
candidate = S.first()
foreach p in S do
if p != hull.last() and p is on the right of the segment
”hull.last(), candidate” then
candidate = p
if candidate != hull.first then hull.push(candidate) else break
return hull
9

Graham's scan
→ Sort the points in clockwise order around
the leftmost point - Cost: O(n log n)
10

Graham's scan
→ Keep the current hull in a stack
H = {h0, . . . , hcurr}.
10

Graham's scan
H = {h0, . . . , hcurr}.
→ Inspect each point p in order - Cost: O(n)
10

Graham's scan
H = {h0, . . . , hcurr}.
→ While hcurr−1hcurrp is a right turn, pop hcurr.
10

Graham's scan
H = {h0, . . . , hcurr}.
→ Push p to H.
10

Graham's scan
H = {h0, . . . , hcurr}.
→ Push p to H.
→ Overall complexity: O(n log n)
10

Graham's scan
Algorithm 2: Graham Scan
Input: a list S of bidimensional points.
Output: the convex hull of the set, sorted counterclockwise.
hull =[]
x0 = the leftmost point.
Put x0 as the first element of S.
Sort the remaining points in counter-clockwise order, with
respect to x0.
Add the first 3 points in S to the hull.
forall the remaining points in S do
while hull.second_to_last(), hull.last(), p form a right turn do
hull.pop()
hull.push(p)
return hull
11

Can we do better?
So far:
→ Jarvis’s march: O(nh)
12

Can we do better?
So far:
→ Graham’s scan: O(n log n)
12

Can we do better?
So far:
→ How do we compare their complexity?
12

Can we do better?
So far:
→ We would like to do even better!
12

Can we do better?
So far:
→ We would like to do even better!
Can we get to O(n log h)?
12

Chan's 2D algorithm
→ Idea: Some points will never be in the hull!
Discard them to speed up Jarvis’s march.
14

Chan's 2D algorithm
→ Combine Jarvis’s march and Graham’s scan.
14

Chan's 2D algorithm
→ Algorithm (Chan 2D):
→ Split the n points in groups of size m
(⌈n/m⌉ groups).
14

Chan's 2D algorithm
(⌈n/m⌉ groups).
→ Compute the hull Hi of each group
Cost: O((n/m) · (m log m)) = O(n log m)
14

Chan's 2D algorithm
(⌈n/m⌉ groups).
→ Until the hull is complete, repeat:
14

Chan's 2D algorithm
(⌈n/m⌉ groups).
→ Given the current hull Htot = {h0, . . . , hcurr},
find for each Hi the point right tangent to
hcurr (binary search, O(log m)⌈n/m⌉).
14

Chan's 2D algorithm
(⌈n/m⌉ groups).
→ Given the current hull Htot = {h0, . . . , hcurr},
find for each Hi the point right tangent to
hcurr (binary search, O(log m)⌈n/m⌉).
→ Pick the tangent point p that maximizes
∠hcurr−1hcurrp.
14

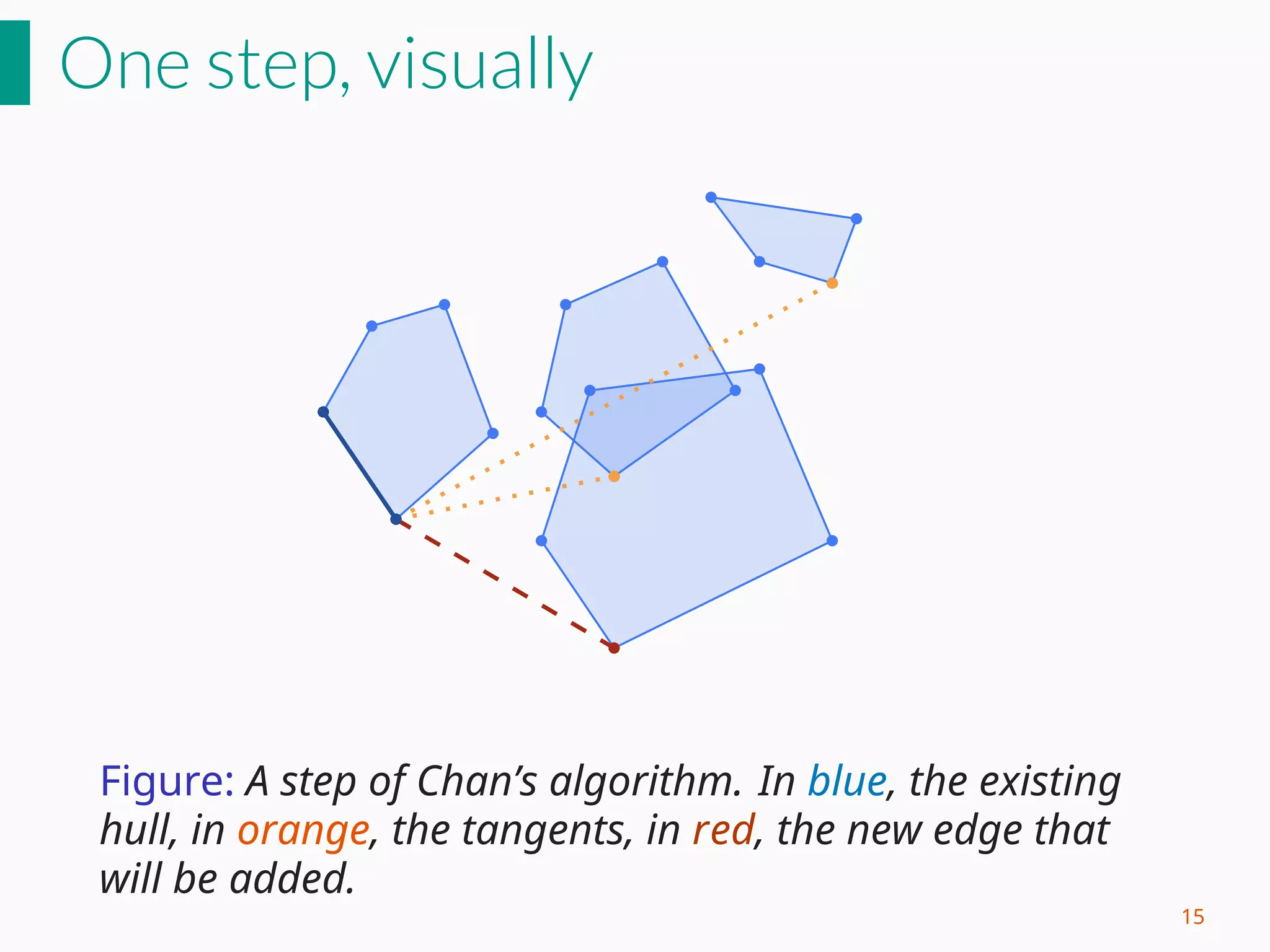
One step, visually
Figure: A step of Chan’s algorithm. In blue, the existing
hull, in orange, the tangents, in red, the new edge that
will be added.
15

Chan's 2D algorithm, part 2
Complexity: O(n log m + (h(n/m)log m))
16

What about m? Let’s pretend the size h of
the final hull is know.
16

With m = h, we get complexity
O(n log h + (h(n/h)log h)) = O(n log h)
16

But h is not known!
16

But h is not known!
→ Reiterate the algorithm, with m = 22i
16

But h is not known!
→ Iteration cost: O(n log H) = O(n2i
)
16

But h is not known!
→ Iteration cost: O(n log H) = O(n2i
)
→ O
(∑⌈log log h⌉
i=1 n2i
)
= O(n2⌈log log h⌉+1
) = O(n log h)
16

Chan's 2D pseudo-code
Algorithm 3: ChanHullStep, a step of Chan’s
algorithm
Input: a list S of bidimensional points, the parameters m, H
Output: the convex hull of the set, sorted counterclockwise, or an empty list, if H
is < h
Partition S into subsets S1, . . . , S⌈n/m⌉.
for i = 1, . . . , ⌈n/m⌉ do
Compute the convex hull of Si by using Graham Scan, store the output in a
counter-clockwise sorted list.
p0 = (0, −∞)
p1 = the leftmost point of S.
for k = 1, . . . , H do
for i = 1, . . . , ⌈n/m⌉ do
Compute the points qi ∈ S that maximizes ∠pk−1pkqi, with qi ̸= pk, by
performing binary search on the vertices of the partial hull Si.
pk+1 = the point q ∈ {q1, . . . , q⌈n/m⌉}.
if pk+1 = pt then return {p1, . . . , pk}
return incomplete
17

Chan's 2D pseudo-code, reprise
Algorithm 4: Chan’s algorithm
Input: a list S of bidimensional points
Output: the convex hull of the set
for i = 1, 2, . . . do
L = ChanHullStep(S, m, H), where m = H = min{|S|, 22i
}
if L ̸= incomplete then return L
18

Chan's 2D - Empirical analysis
Is a real implementation O(n log h)?
Test 1: fixed hull size (1000), increasing number of
points.
0
10
20
30
40
50
50000
100000
150000
200000
Number of Points
Executiontime[sec]
Linear Model Real Data
19

Chan's 2D - Empirical analysis
Is a real implementation O(n log h)?
Test 2: fixed number of points (40000), increasing
hull size.
8
9
10
11 5000
10000
15000
20000
Size of the Hull
Executiontime[sec]
Logarithmic Model Real Data
20

Chan's 3D algorithm
→ Idea: The structure of the algorithm doesn’t
change, just the ingredients.
22

Chan's 3D algorithm
Given a set S of n points with an hull of size h:
22

Chan's 3D algorithm
→ Jarvis's march −→ Chand and Kapur's gift
wrapping - O(nh).
22

Chan's 3D algorithm
wrapping - O(nh).
→ Graham's scan −→ Preparata and Hong 3D
Algorithm - O(n log n).
22

Chan's 3D algorithm
wrapping - O(nh).
→ Finding tangents in 2D −→ Supporting planes
in 3D with Dobkin-Kirkpatrick hierarchy -
O(log n).
22

Chan's 3D algorithm
wrapping - O(nh).
→ Finding tangents in 2D −→ Supporting planes
in 3D with Dobkin-Kirkpatrick hierarchy -
O(log n).
The overall complexity is still O(n log h).
22

Chan's 3D algorithm
→ 3D Gift wrapping
23

Chan's 3D algorithm
→ Pick an edge ej of a face f of the partial hull.
23

Chan's 3D algorithm
→ Find p that maximizes the angle between f and
the new face given by ej and p. Repeat for the 3
edges of f.
23

Chan's 3D algorithm
edges of f.
→ Use breadth first visit to build the entire hull.
23

Chan's 3D algorithm
edges of f.
→ Preparata and Hong 3D algorithm, a
divide-and-conquer algorithm for convex
hulls
23

Chan's 3D algorithm
edges of f.
hulls
→ Split the set of points S in S1 and S2.
23

Chan's 3D algorithm
edges of f.
hulls
→ Recursively split until the base case, then build
the convex hull.
23

Chan's 3D algorithm
edges of f.
hulls
→ Recursively split until the base case, then build
the convex hull.
→ Merge the partial hulls.
23

Chan's 3D algorithm
→ To find supporting planes, store each partial
hull as a Dobkin-Kirkpatrick hierarchy
24

Chan's 3D algorithm
→ Sequence P0, . . . , Pk of increasingly smaller
approximations of a polyhedron P = P0.
24

Chan's 3D algorithm
→ Build Pi+1 from Pi by picking a maximal set of
independent vertices of Pi.
24

Chan's 3D algorithm
→ Overall, building the hierarchies takes O(n).
24

Chan's 3D algorithm
→ Finding supporting planes in 3D
24

Chan's 3D algorithm
→ Goal: given an edge ej and the DK hierarchy of a
partial hull Hi, find the plane passing through ej
and tangent to Hi in pt.
24

Chan's 3D algorithm
→ Find pt in constant time in Pk
24

Chan's 3D algorithm
→ Step up in the hierarchy: if pt changes, it will
move to a neighbour (constant time check).
24

Chan's 3D algorithm
→ Step up in the hierarchy: if pt changes, it will
move to a neighbour (constant time check).
→ The DK hierarchy has O(log m) height.
24

References I
[1] C. Bradford Barber, David P. Dobkin, and Huhdanpaa Hannu.
The quickhull algorithm for convex hulls.
1995.
[2] T. M. Chan.
Optimal output-sensitive convex hull algorithms in two and three
dimensions.
Discrete & Computational Geometry, 16(4):361–368, 1996.
[3] Donald R. Chand and Sham S. Kapur.
[4] Ioannis Z. Emiris and John F. Canny.
An efficient approach to removing geometric degeneracies.
Technical report, 1991.
[5] Christer Ericson.
Real-Time Collision Detection.
CRC Press, Inc., Boca Raton, FL, USA, 2004.
[6] A. Goshtasby and G. C. Stockman.
Point pattern matching using convex hull edges.
IEEE Transactions on Systems, Man, and Cybernetics, SMC-15(5), 1985.
26

References II
[7] David G. Kirkpatrick and Raimund Seidel.
The ultimate planar convex hull algorithm ?
Technical report, 1983.
[8] Joseph O’Rourke.
Computational Geometry in C.
Cambridge University Press, 2nd edition, 1998.
[9] F. P. Preparata and S. J. Hong.
Convex hulls of finite sets of points in two and three dimensions.
Commun. ACM, 20(2):87–93, February 1977.
[10] Franco P. Preparata and Michael I. Shamos.
Computational Geometry: An Introduction.
Springer-Verlag New York, Inc., 1985.
[11] Franco P. Preparata and Michael I. Shamos.
Computational Geometry: An Introduction.
Springer-Verlag New York, Inc., 1985.
Beamer theme: Presento, by Ratul Saha. The research system in Germany, by
Hazem Alsaied
27

Convex hulls & Chan's algorithm

More Related Content

What's hot

Viewers also liked

Similar to Convex hulls & Chan's algorithm

Recently uploaded

Convex hulls & Chan's algorithm