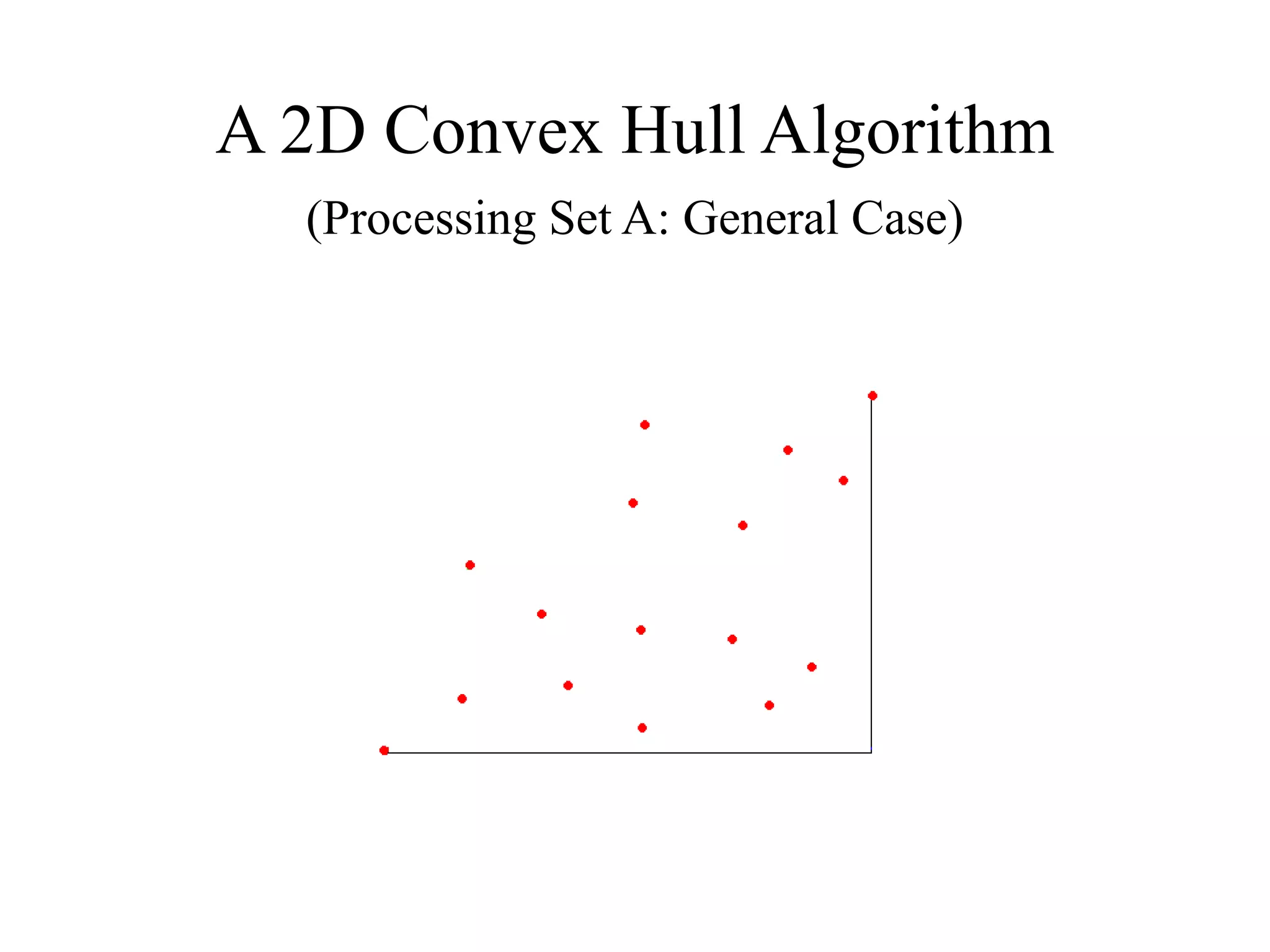
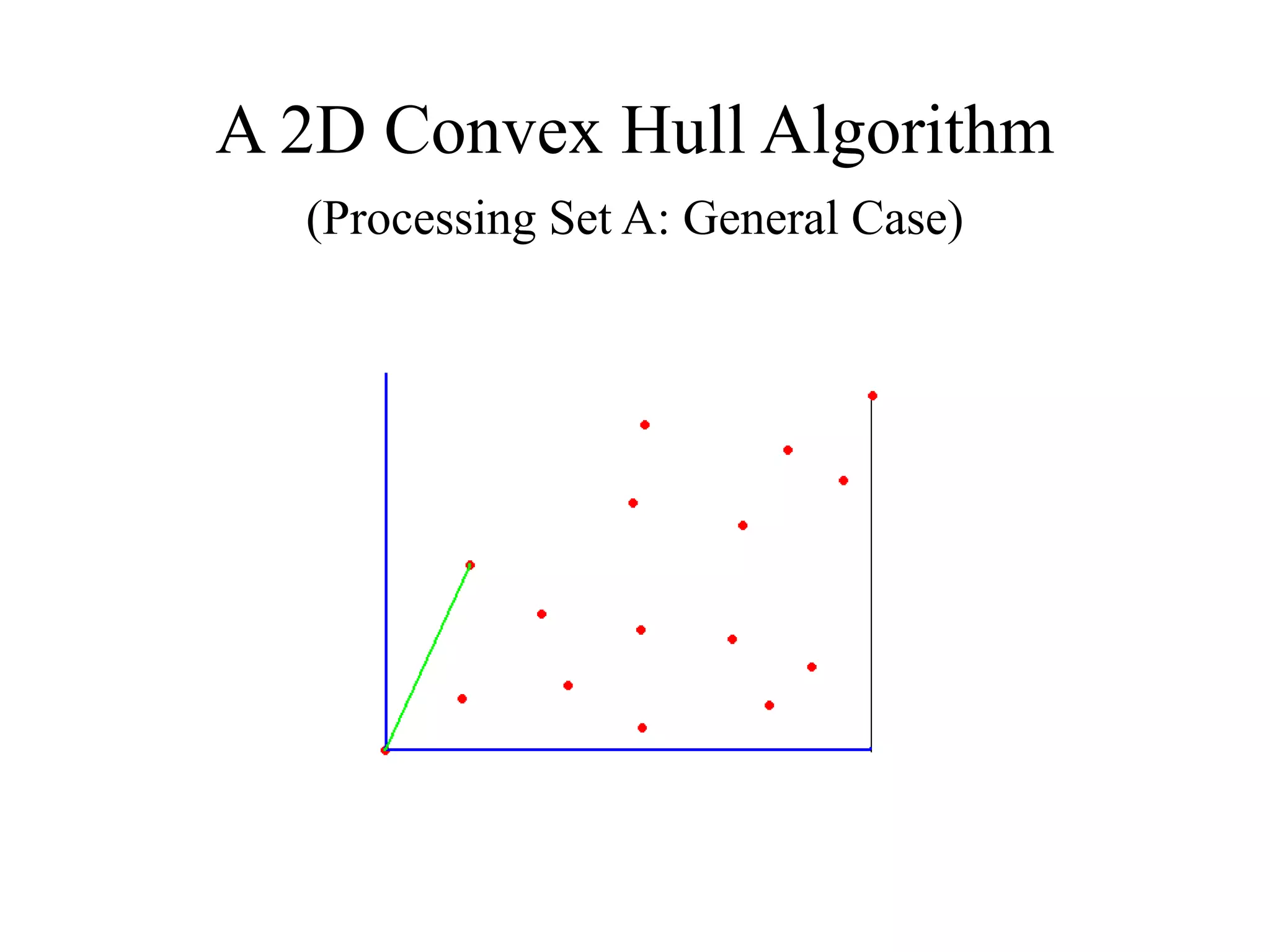
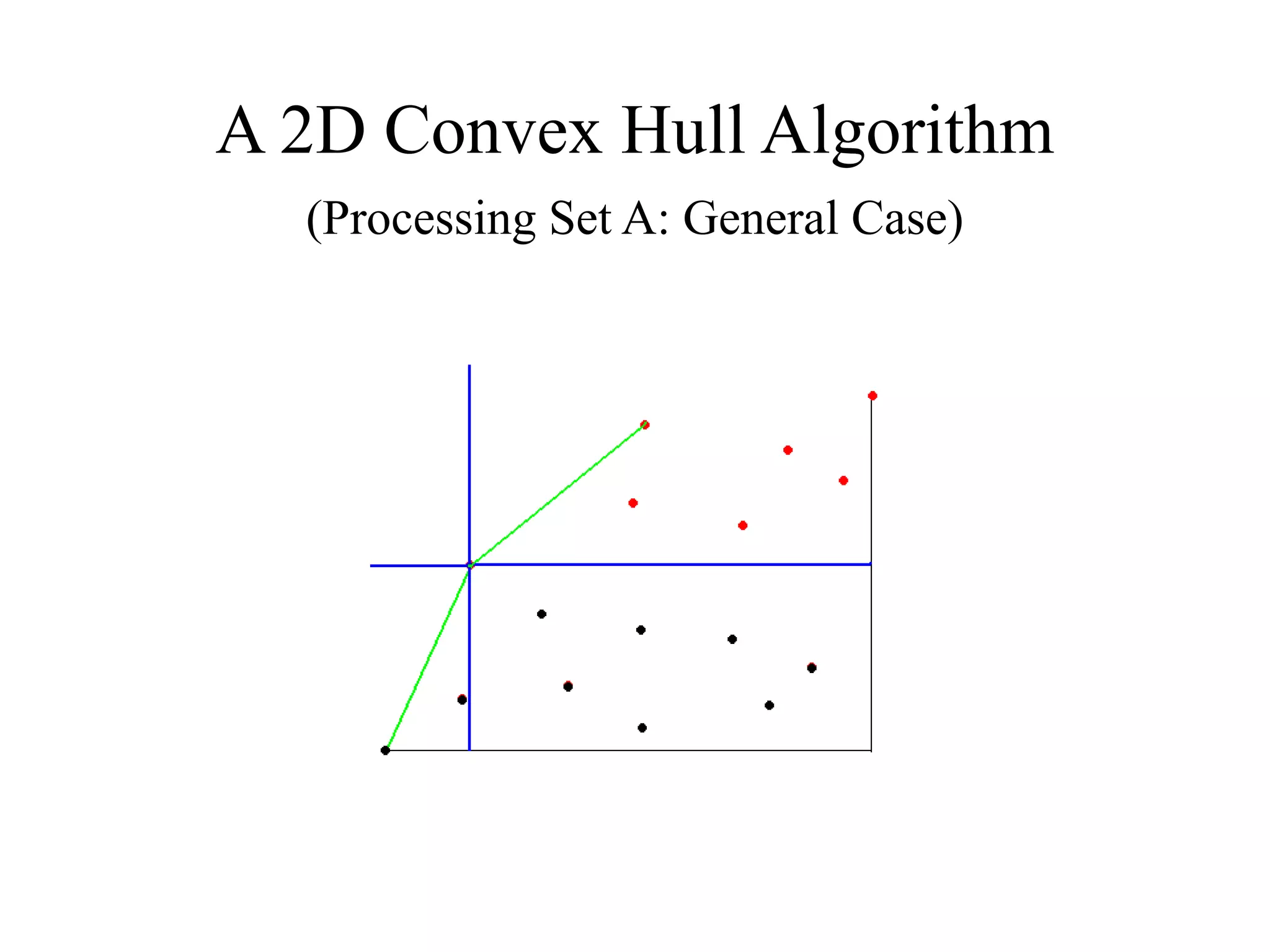
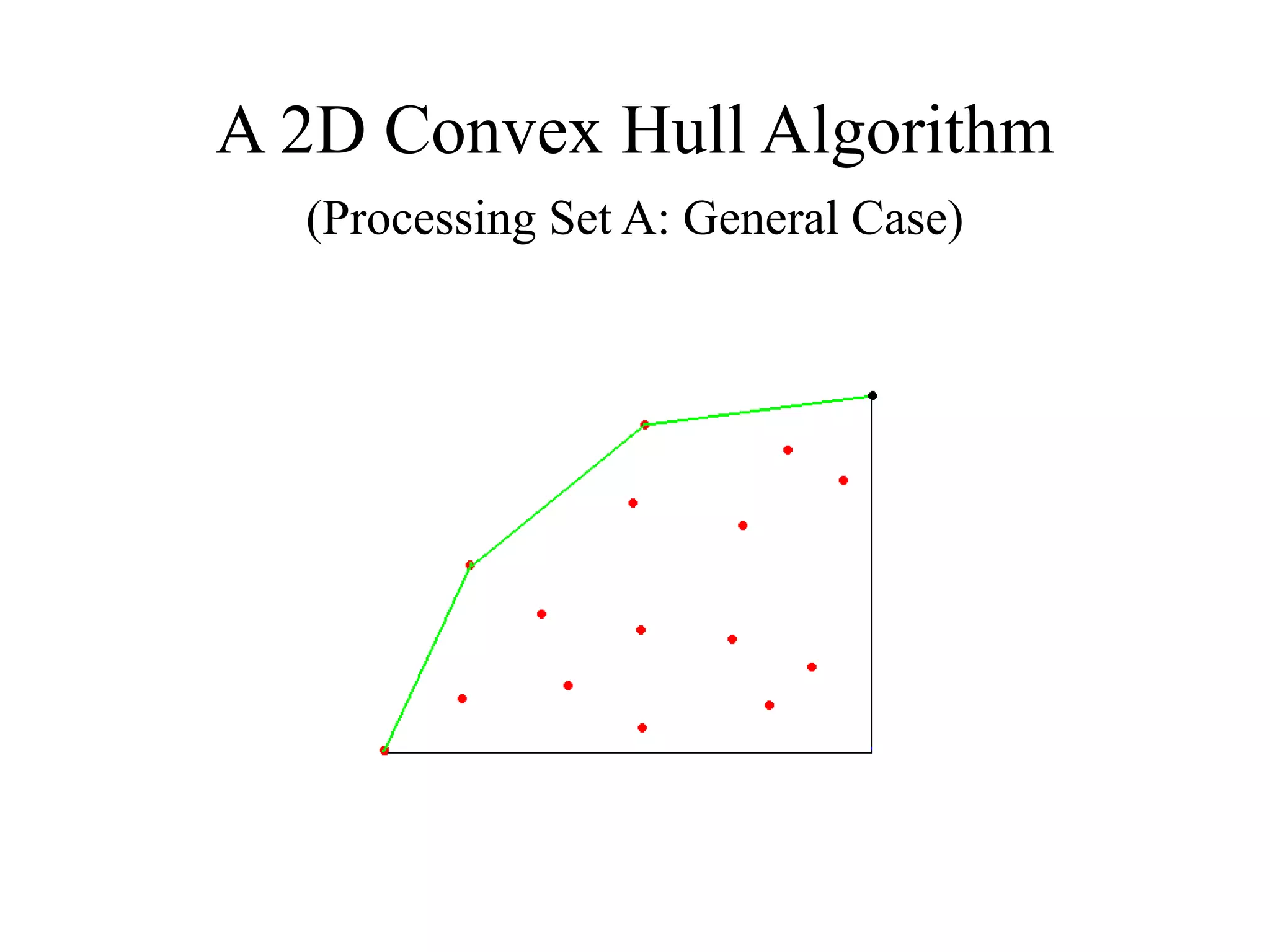
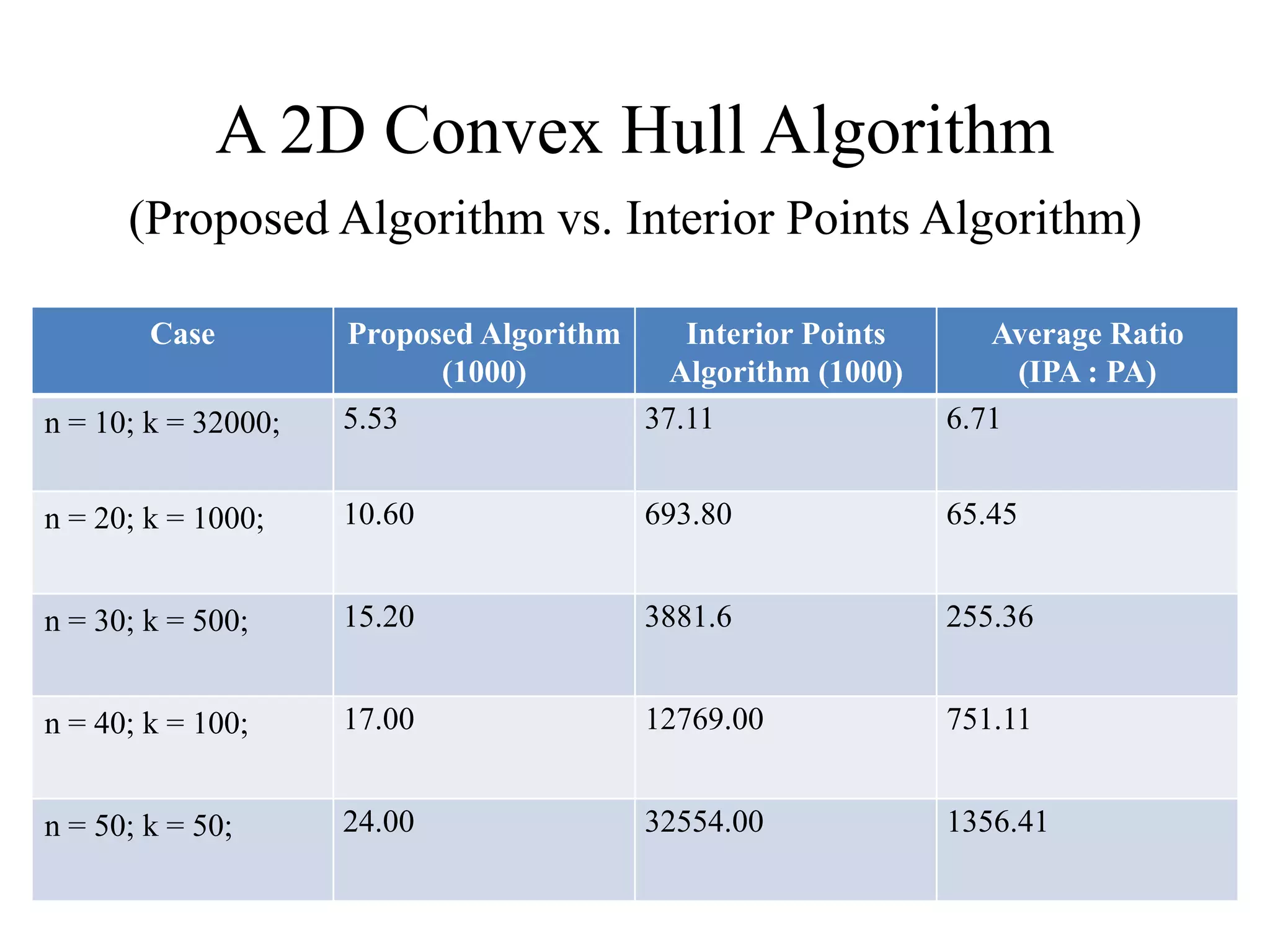
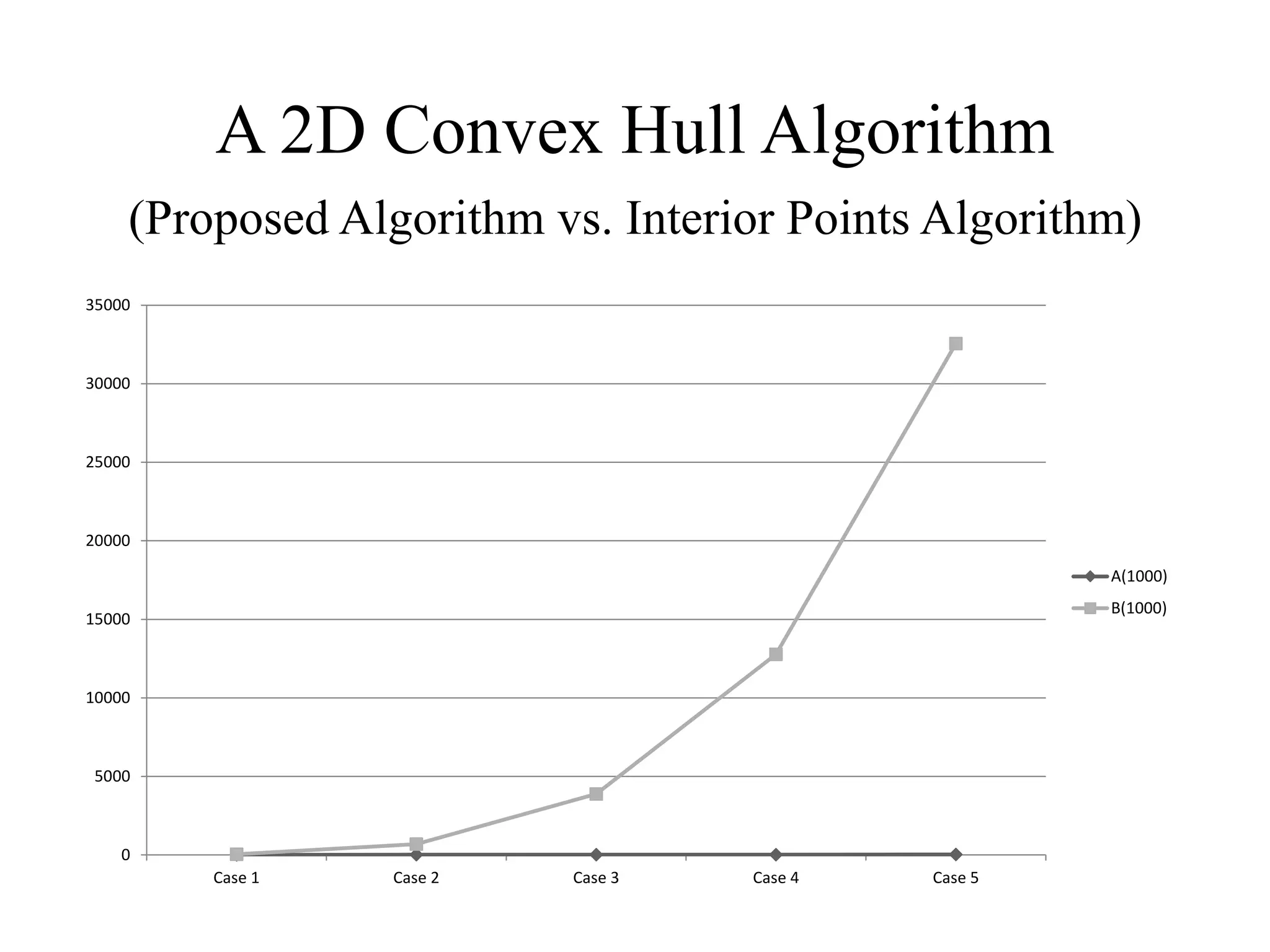
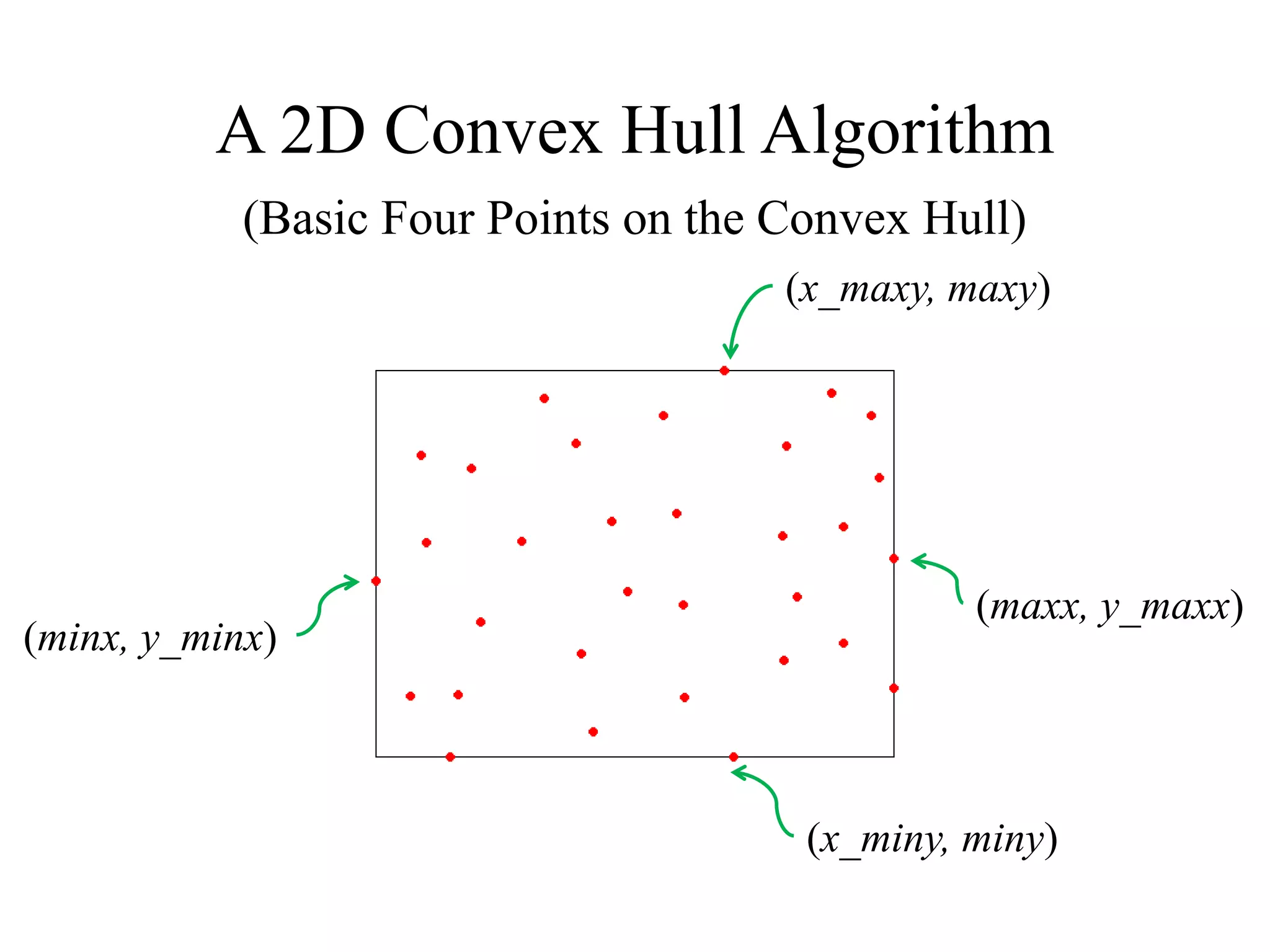
An Efficient Convex Hull Algorithm for a Planer Set of Points

An Efficient Convex Hull Algorithm
for a Planer Set of Points
Kasun Ranga Wijeweera
(krw198708298@gmail.com)

This Presentation is Based on
Following Research Paper
K. R. Wijeweera, U. A. J. Pinidiyaarachchi (2013), An
Efficient Convex Hull Algorithm for a Planer Set of Points,
Ceylon Journal of Science (Physical Sciences), Volume 17, pp.
9-17.

Definitions
(Convex Set)
• A set S is convex if x in S and y in S implies that the segment
xy is a subset of S
• Example in 2D:

Definitions
(Convex Hull of a Set of Points)
• The convex hull of a set S of points is the smallest convex set
containing all the points in S
• Example in 2D:

A 2D Convex Hull Algorithm
(Introduction)
• This algorithm is based on gradient in coordinate geometry
• Achieves parallelism
• Achieves data reduction
• Manages coincident points
• Deals with collinear points
• Outputs hull points in boundary traversal order
• Low computational cost

(Inputs and Outputs)
• Input: A non-empty set of points
S = {P1, P2, . . . , Pn}
• Output: A non-empty set that contains all the points of the
convex hull of S
H = {Q1, Q2, . . . , Qm}

(Example Data Set)
x
y

(Step 1)
Calculate following values from the set S
minx // minimum value of x-coordinates
y_minx // y-coordinate corresponding to minx
maxx // maximum value of x-coordinates
y_maxx // y-coordinate corresponding to maxx
miny // minimum value of y-coordinates
x_miny // x-coordinate corresponding to miny
maxy // maximum value of y-coordinates
x_maxy // x-coordinate corresponding to maxy

(Basic Four Points on the Convex Hull)
(x_maxy, maxy)
(minx, y_minx)
(maxx, y_maxx)
(x_miny, miny)

(Step 2)
Define following subsets of S
A = { ( x, y) in S | ( x <= x_maxy ) AND ( y >= y_minx )}
B = { ( x, y) in S | ( x >= x_maxy ) AND ( y >= y_maxx )}
C = { ( x, y) in S | ( x >= x_miny ) AND ( y <= y_maxx )}
D = { ( x, y) in S | ( x <= x_miny ) AND ( y <= y_minx )}

(Partitioning the Data Set into Four Regions)
A B
CD

(Step 3)
• Find the convex hull parts belong to each of the sets A, B, C,
and D in parallel
• Merge those hull parts to derive the set H

(After Processing and Merging Hull Parts)
A B
CD

(Processing Each Set: Gradient)
x
y
M (mx, my)
N (nx, ny)
m = ( ny – my ) / ( nx – mx )

(Processing Each Set: Modified Gradient)
A B
CD

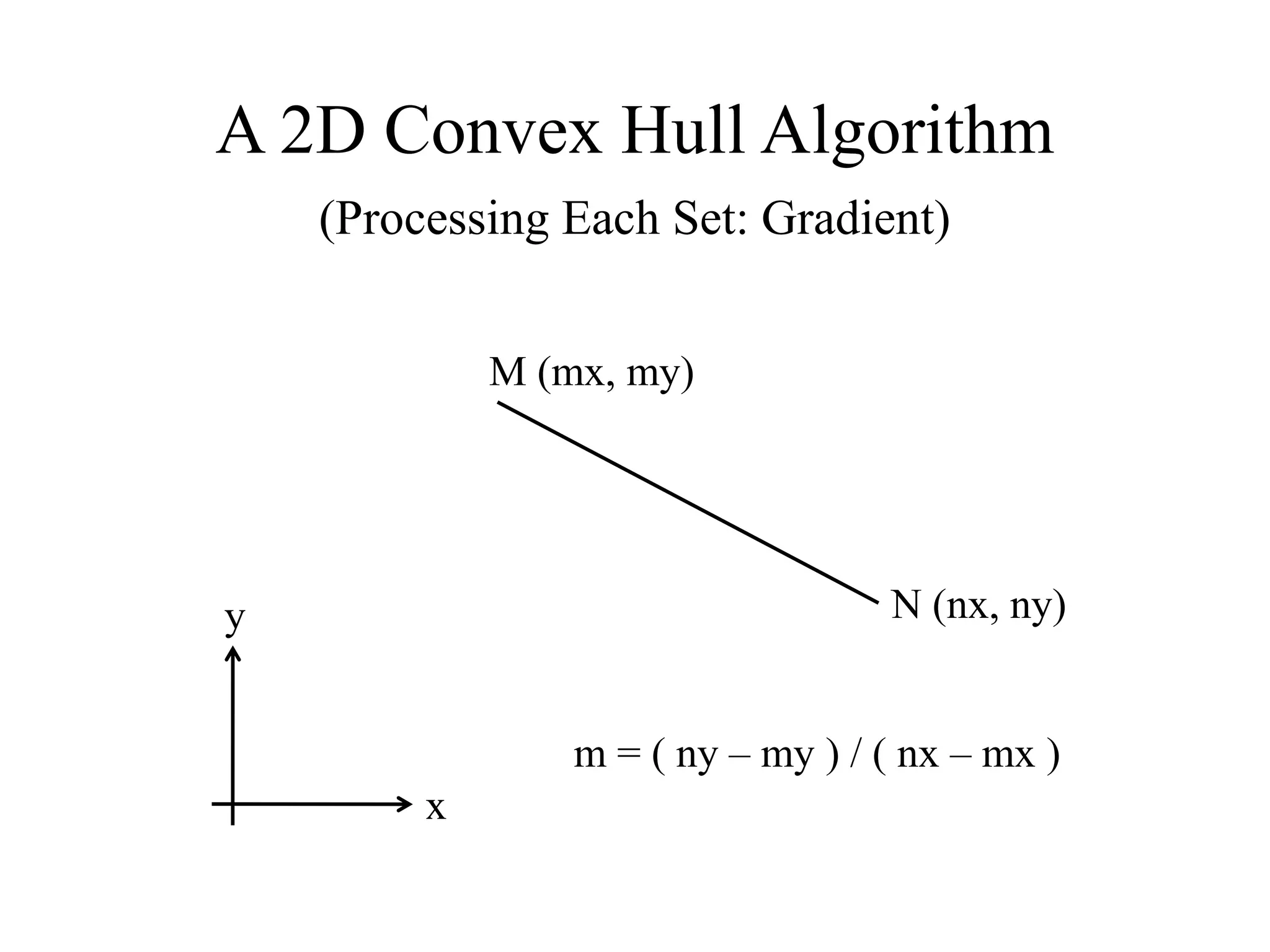
(Processing Each Set: Modified Gradient)
Region Diagram Modified Gradient Begin Point End Point
A ( ay[i] – hully ) / ( ax[i] – hullx ) x = minx
y = y_minx
x = x_maxy
y = maxy
B ( bx[i] – hullx ) / (hully - by[i] ) x = x_maxy
y = maxy
x = maxx
y = y_maxx
C ( hully - cy[i] ) / ( hullx - cx[i] ) x = maxx
y = y_maxx
x = x_miny
y = miny
D ( hullx – dx[i] ) / ( dy[i] – hully ) x = x_miny
y = miny
x = minx
y =y_minx

(Processing Set A: General Case)

(Processing Set A: Collinear Case)

(Processing Set A: Indeterminate Case)

(Processing Sets B, C, and D)
• Using similar method B, C, and D sets can also be processed
• Using the same algorithm used for A to process B, C, and D
needs additional computational cost
• Therefore four separate algorithms are used to process each of
four sets with modified gradient

(Interior Points Algorithm)
Based on the following Lemma
A point is non-extreme if and only if it is inside some (closed)
triangle whose vertices are points of the set and is not itself a
corner of that triangle

(Interior Points Algorithm)
Algorithm: INTERIOR POINTS
for each i do
for each j != i do
for each k != i != j do
for each l != k != i != j do
if p(l) in Triangle{ p(i), p(j), p(k) }
then p(l) is non-extreme

(Proposed Algorithm vs. Interior Points Algorithm)
• Both of the algorithms were implemented using C++
programming language
• Following hardware and software resources were used
– Computer: Intel(R) Pentium(R) Dual CPU; E2180 @ 2.00 GHz; 2.00
GHz, 0.98 GB of RAM;
– IDE: Turbo C++; Version 3.0; Copyright(c) 1990, 1992 by Borland
International, Inc;

• First, n number of random points were generated in the range 0
– 399 using randomize() function and written them to a text
file
• Such text files were generated for different n
• Number of clock cycles taken to process each data file k times
was counted using clock() function

Case Proposed Algorithm
(1000)
Interior Points
Algorithm (1000)
Average Ratio
(IPA : PA)
n = 10; k = 32000; 5.53 37.11 6.71
n = 20; k = 1000; 10.60 693.80 65.45
n = 30; k = 500; 15.20 3881.6 255.36
n = 40; k = 100; 17.00 12769.00 751.11
n = 50; k = 50; 24.00 32554.00 1356.41

0
5000
10000
15000
20000
25000
30000
35000
Case 1 Case 2 Case 3 Case 4 Case 5
A(1000)
B(1000)

(Drawbacks of the Proposed Algorithm)
• It cannot be easily extended to higher dimensions
• The notion of gradient causes the problem
• Need to solve partial differential equations in order to derive
the gradient
• Because of this higher dimensional extension is not cost
effective
• The entire data set is needed from the beginning
– The algorithm is static

An Efficient Convex Hull Algorithm for a Planer Set of Points

More Related Content

What's hot

Viewers also liked

Similar to An Efficient Convex Hull Algorithm for a Planer Set of Points

More from Kasun Ranga Wijeweera

Recently uploaded

An Efficient Convex Hull Algorithm for a Planer Set of Points