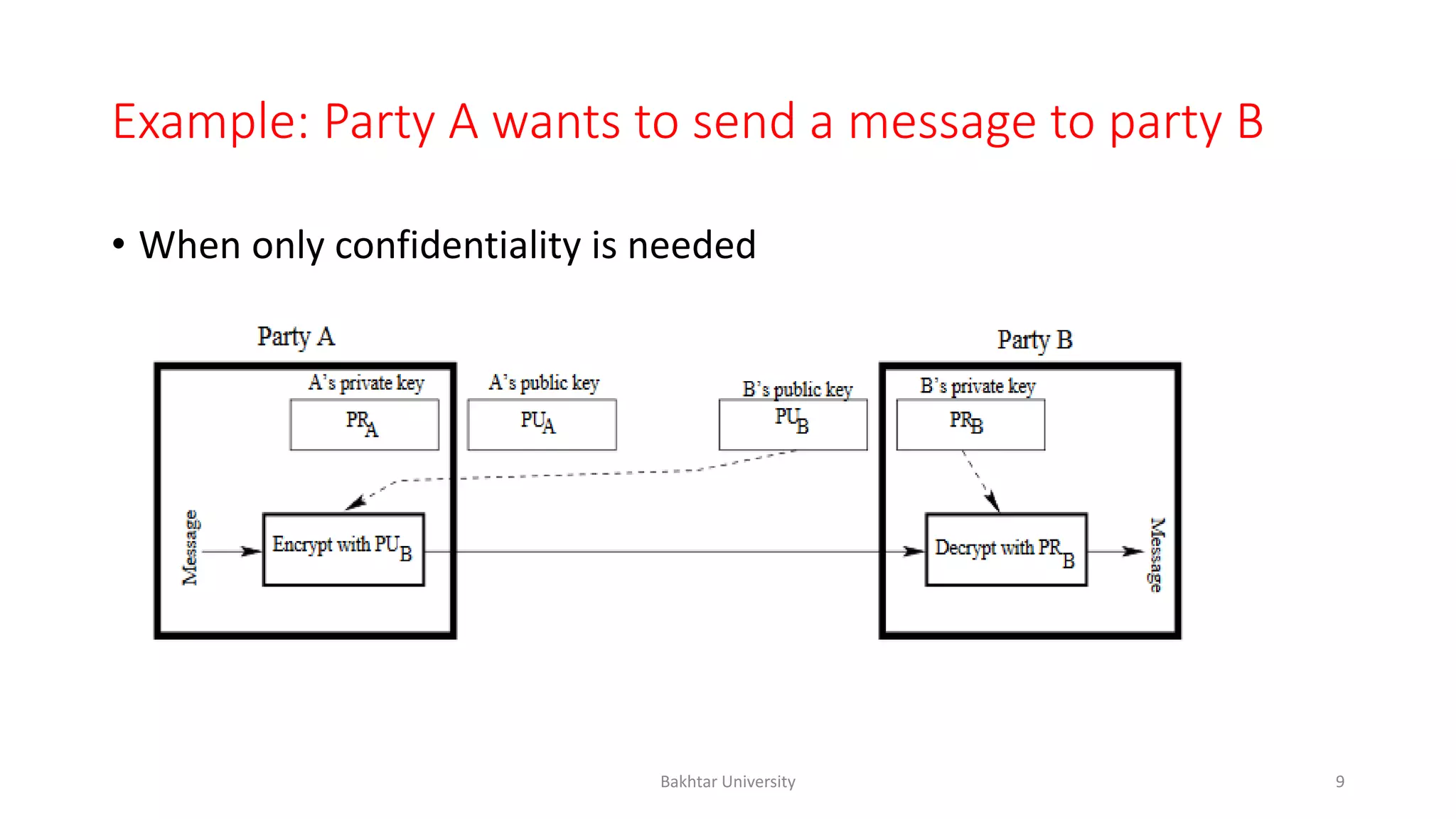
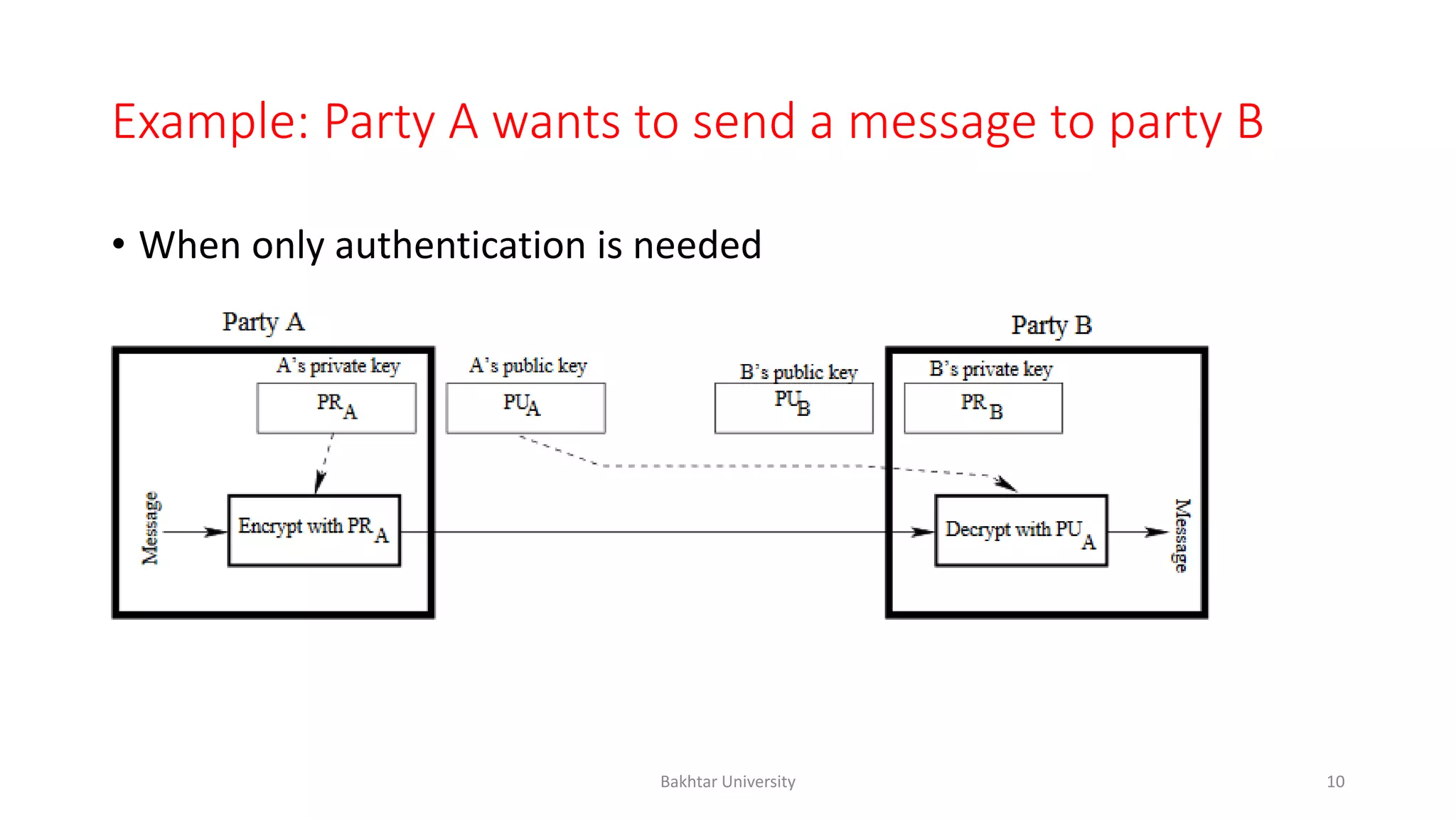
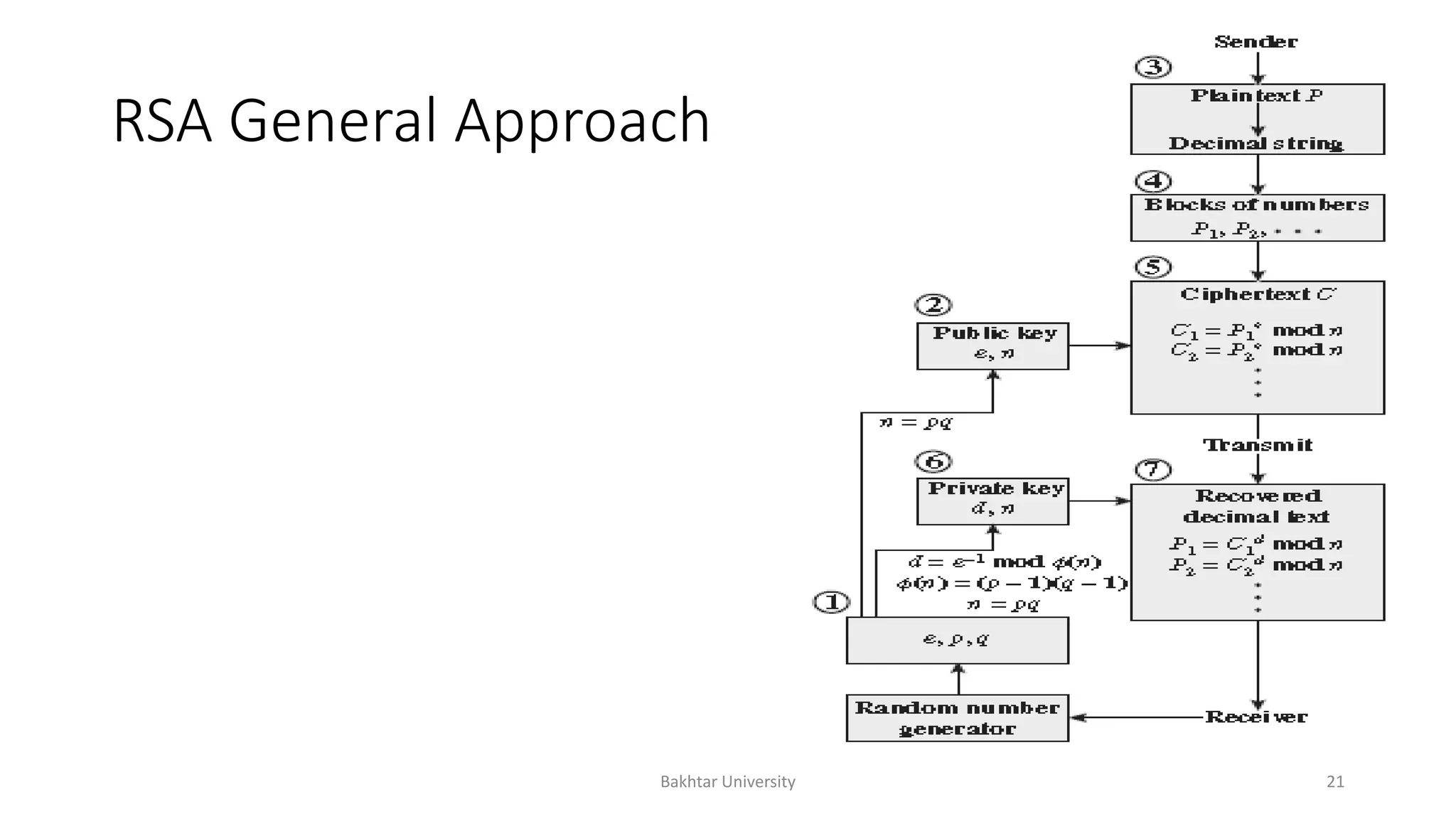
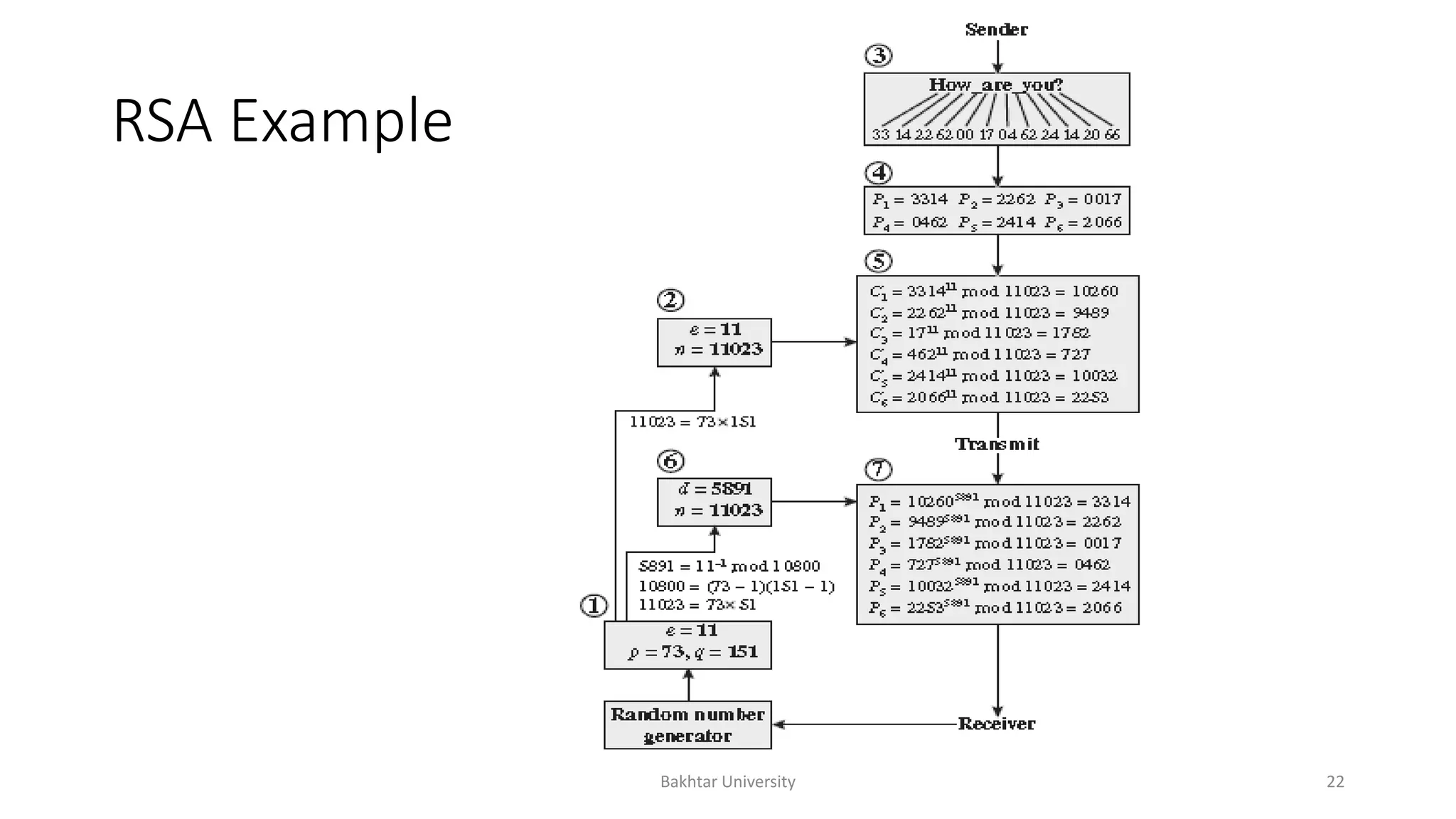
The document discusses asymmetric cryptography, highlighting issues with symmetric cryptography such as key distribution and scalability. It details the use of public-key cryptography, exemplified by the RSA algorithm, which allows secure communication between parties without prior key sharing. RSA involves generating a public and private key pair based on large prime numbers, ensuring the security of encrypted messages through the difficulty of factoring large integers.